Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

432 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

Figure 14.12: Euclid’s elements (Example 2).

14.9.3 CONFORMAL PRIMITIVES AND INTERSECTIONS

In this example we repeat the blade visualization example of Section 11.13.2, only this

time in the conformal setting that considerably extends the blades to be drawn. Again

the user can create and drag points, and create primitives by selecting a number of these

points. The primitives that can be constructed are lines, planes, circles, and spheres.

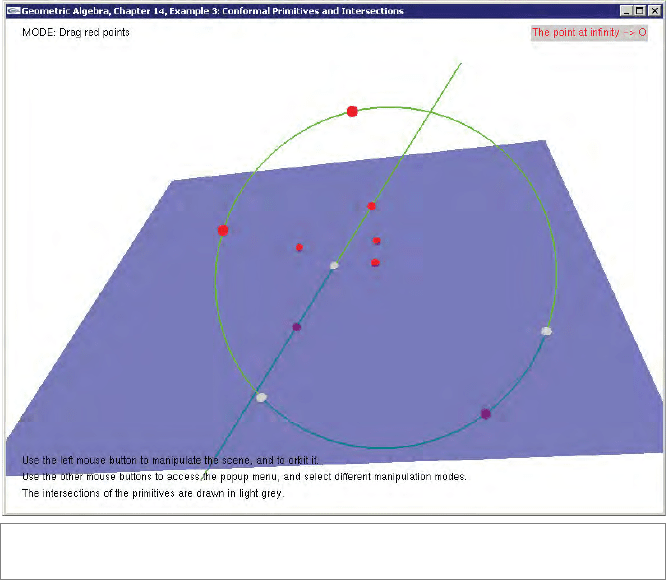
The example draws all these primitives and their intersections. A screenshot is shown in

Figure 14.13.

A circle is created by selecting three points. If one of these points is the point at

inﬁnity—which for this occasion is located conveniently in the upper-right corner of the

viewport—then a line is created. Circles and lines can be computed using the same code,

because a line is just a special type of circle (i.e., one that passes through inﬁnity):

circle C = _circle(g_points[pointIdx1] ^ g_points[pointIdx2] ^

g_points[pointIdx3]);

Spheres and planes are created by selecting four points, and computed as follows:

sphere S = _sphere(g_points[pointIdx1] ^ g_points[pointIdx2] ^

g_points[pointIdx3] ^ g_points[pointIdx4]);

Again, a plane is a special type of sphere for which one of the selected points is inﬁnity.

SECTION 14.9 PROGRAMMING EXAMPLES AND EXERCISES 433

Figure 14.13: Example 3 in action.

The intersections of the primitives are computed by the following code, which spells out

the

meet:

// P1 and P2 are two multivectors (the primitives)

I = unit_e(join(P1, P2));

mv intersection = (P1 << I) << P2;

As in Section 11.13.2, we use orthogonal projection to enable the creation of degenerate

situations.

// P1 and P2 are two multivectors (the primitives)

mv projection = (P1 << inverse(P2)) << P2;

// check if projection of P1 onto P2 is ’close’ to P1

const float CLOSE = 0.02f;

if (_Float(norm_e(projection — P1)) < CLOSE) {

// yes: P1 = projection of P1 onto P2

P1 = projection;

}

434 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

This projection step is of course performed before the intersection test, not after. Note that

orthogonal projections involving round conformal objects do not behave as you would

expect, as this would result in conics (which the conformal model obviously cannot rep-

resent). For more details, see Section 15.3.

Creating Points

Just as in Section 11.13.2, new points can be created by a mouse-click. The user then

expects a point to appear under the mouse cursor. The code to create a point at the cor-

rect location is very similar to that in Section 11.13.2, except that this time we use a versor

to apply the inverse modelview transformation (in the homogeneous example, we con-

structed an outermorphism directly from the inverted modelview matrix):

// create point at required location and ’distance’

point pt = _point(c3gaPoint(_vectorE3GA(vectorAtDepth(distance,

mousePos) — e3 * distance)));

// retrieve modelview matrix from OpenGL:

float modelviewMatrix[16];

glGetFloatv(GL_MODELVIEW_MATRIX, modelviewMatrix);

// convert modelview matrix to versor:

bool transpose = true;

TRversor V = _TRversor(matrix4x4ToVersor(modelviewMatrix, transpose));

// apply (inverse) OpenGL ’versor’ to transform the point to the

// global frame

pt = inverse(V) * pt * V;

The function matrix4x4ToVersor() will be discussed in Section 16.10.1. It converts 4×4

translate-rotate-scale matrices into conformal versors.

14.9.4 FITTING A SPHERE TO A SET OF POINTS

This example implements the equations for ﬁtting a sphere from Section 14.5. The user

can drag and create points, as in the previous example. The program tries to ﬁt a sphere to

these points as well as it can under the least-squares condition. As noted in Section 14.5,

the minimization criterion has a preference for small spheres.

The code, shown in Figure 14.14, is straightforward to implement given the algorithm

that was spelled out in Section 14.5:

•

The matrix P =



[[ p

]] [[ p

]]

is computed;

•

Then, the metric matrix M is initialized;

•

The product of these matrices is computed PM=P*M;

•

The singular value decomposition (SVD) is computed, resulting in the matrices U,

S, and V;

•

The coordinates of the dual sphere DS are set to the last column of V.

SECTION 14.9 PROGRAMMING EXAMPLES AND EXERCISES 435

dualSphere fitSphere(const std::vector<point> &points) {

float P[5 * 5];

// compute matrix P = sum_i (points[i] . points[i]^T)

{

// first clear all entries:

for (int i=0;i<5*5;i++) P[i] = 0.0f;

// fill the matrix:

for (unsigned int p = 0; p < points.size(); p++) {

// get coordinates of point ’p’:

const mv::Float *pc = points[p].getC(point_no_e1_e2_e3_ni);

for (int i=0;i<5;i++)

for (int j=i;j<5;j++) {

P[i*5+j]+=pc[i] * pc[j];

P[j*5+i]=P[i*5+j];

}

// initialize the metric matrix:

float M[5*5]={

// no e1 e2 e3 ni

0.0f, 0.0f, 0.0f, 0.0f, -1.0f, // no

0.0f, 1.0f, 0.0f, 0.0f, 0.0f, // e1

0.0f, 0.0f, 1.0f, 0.0f, 0.0f, // e2

0.0f, 0.0f, 0.0f, 1.0f, 0.0f, // e3

-1.0f, 0.0f, 0.0f, 0.0f, 0.0f // ni

};

// construct OpenCV matrices (on stack)

CvMat matrixP = cvMat(5, 5, CV_32F, P);

CvMat matrixM = cvMat(5, 5, CV_32F, M);

// use OpenCV to multiply matrices

float PM[5 * 5];

CvMat matrixPM = cvMat(5, 5, CV_32F, PM); // create matrixP*M(onstack)

cvMatMul(&matrixP, &matrixM, &matrixPM);

// use OpenCV to compute SVD

float S[5 * 5], U[5 * 5], V[5 * 5];

CvMat matrixS = cvMat(5, 5, CV_32F, S); // create matrix S (on stack)

CvMat matrixU = cvMat(5, 5, CV_32F, U); // create matrix U (on stack)

CvMat matrixV = cvMat(5, 5, CV_32F, V); // create matrix V (on stack)

int flags = 0;

cvSVD(&matrixPM, &matrixS, &matrixU, &matrixV, flags);

// extract last column of V (coordinates of dual sphere);

dualSphere DS(dualSphere_no_e1_e2_e3_ni,

V[0*5+4],V[1*5+4],V[2*5+4],V[3*5+4],V[4*5+4]);

return DS;

}

Figure 14.14: Fitting-a-sphere code.

436 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

The OpenCV library is used to implement the linear algebra operations (matrix

multiplication and SVD).

Interestingly, the sphere-ﬁtting-algorithm will come up with a plane when this is the opti-

mal solution! As an easy way to create this situation, we have provided an option in a

popup menu that projects all points onto the e

∗

plane.

CONSTRUCTIONS IN

EUCLIDEAN GEOMETRY

Now that the previous chapters have given us such a range of elements of Euclidean

geometry as the blades in the conformal model, we want to combine them into

useful constructions. As always, this is no more than the application of operations we

introduced in Part I, but they take on intriguing and useful meanings.

The

meet is greatly extended in its capabilities to intersect arbitrary ﬂats and rounds

(though always with the same formula X∩Y = Y

∗

X), or to compute other incidences.

The results can be real or imaginary, or even the inﬁnitesimal tangents. The dual of the

meet provides a novel operation: the plunge, which constructs the simplest element

intersecting a given group of elements perpendicularly. Once recognized, you will spot

it in many constructions, and it enables you to quickly write down correct expressions

for, say, the contour circle of a sphere seen from a given point.

We show how all the various concepts of a vector in classical geometry ﬁnd their spe-

ciﬁc expression in the conformal model. Normal vector, position vector, free vector,

line vector, and tangent vector now all automatically move in the correct way under

the same Euclidean rotors. This demonstrates clearly that the conformal model per-

forms both the geometrical computations and the “data type management” required

in Euclidean geometry.

We conclude with a sample analysis of some involved planar geometry (the geometry of a

Voronoi cell), and compare the coordinate-free conformal solution to the many parame-

ters involved in even just specifying the classical solution.

437

438 CONSTRUCTIONS IN EUCLIDEAN GEOMETRY CHAPTER 15

15.1 EUCLIDEAN INCIDENCE AND COINCIDENCE

The basic constructions in geometric algebra are spanning and intersection. In the vector

space model prevalent in Part I, these were fairly straightforward operations on subspaces

through the origin. They still are in the representational space of the conformal model, but

their interpreted Euclidean consequences deserve careful study. They offer a rich syntax

for a constructive and consistent speciﬁcation language for Euclidean geometry.

15.1.1 INCIDENCE REVISITED

We have encountered the meet in a general context in Chapter 5. Within the conformal

model, we used it in the previous chapter to construct elements by intersection with other

elements. Since the basic elements of point, sphere, and plane are all dually represented

as vectors, it was easiest to study the

meet in its dual form:

(A ∩ B)

∗

= B

∗

∧ A

∗

If your application involves a lot of intersections, it is often convenient to stay in the dual

representation. However, you should still be careful: the duality in the

meet needstobe

taken relative to the

join, which may change for successive meet operations, so you may

not be able to use a single dual representation of an element for all its uses.

The principle of the

meet is that it constructs the largest subblade common to the blades

A and B. The duality relative to the

join constructs the complements within the smallest

blade containing both; these complements do not contain common factors, so that their

outer product is nonzero. In that sense, they are independent blades. With that, the con-

tainment relationship that gives us the

meet is easily veriﬁed in its dual form:

0 = x(A ∩ B)

∗

= x(B

∗

∧ A

∗

) = (xB

∗

) ∧ A

∗



∗

∧ (xA

∗

and the constructed independence of A

∗

and B

∗

then implies that x is contained in (A∩B)

if and only if it is contained in both A and B. This is easily extended by associativity. Three

intersecting spheres, dually represented by a, b, c, will

meet in the point pair (a ∧ b ∧ c)

−∗

(where the join is the full pseudoscalar); see Figure 15.1(a).

In the conformal model, the

meet of two elements may be imaginary. For instance, the

meet of three spheres that do not really intersect is an imaginary point pair. The dual of

this imaginary point pair is a real circle; see Figure 15.1(b). When we draw that using visu-

alization software, we ﬁnd that this real circle intersects the original spheres perpendic-

ularly. This bears investigating: can we construct elements that perpendicularly intersect

other elements by taking the dual of the

meet?

15.1.2 CO-INCIDENCE

Let us consider what kind of element is constructed by the dual operation to the meet.

Its deﬁnition would be that its direct representation is B

∗

∧ A

∗

.Ifwecallthemeet

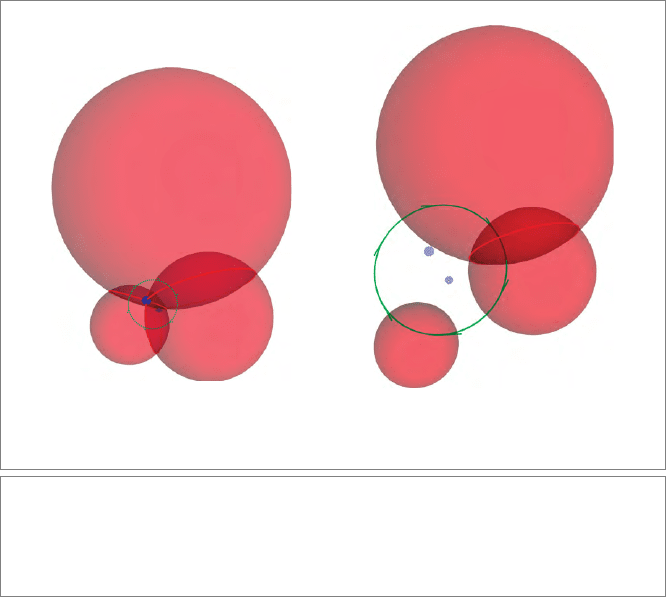
SECTION 15.1 EUCLIDEAN INCIDENCE AND COINCIDENCE 439

(b)

(a)

Figure 15.1: (a) The meet of three intersecting dual spheres a, b, c is the real point pair with

dual representation c ∧ b ∧ a (in blue), whereas their

plunge is an imaginary (dashed) circle. (b)

The

plunge of three nonintersecting spheres is the circle with direct representation c ∧ b ∧ a

(in green), while their

meet is an imaginary (speckled) point pair. To assist 3-D interpretation,

some real intersection circles are indicated in red.

the incidence, we could call this “co-incidence”, in the algebraic jargon that associates

“co-” with “dual.”

When we treated the scalar product in Section 3.1.4, we saw that two blades A and B

of the same grade are orthogonal to each other when their scalar product is zero. This

is equivalent to the scalar product of their duals being zero, since the scalar product of

elements or their duals differ only by a sign (do structural exercise 1 if you want to know

which sign). For blades of nonequal grades, this extends to their contractions, although

the order now matters (since the contraction of a higher-grade blade onto a lower-grade

blade is trivially zero anyway). For a blade X of grade smaller than A to be perpendicular

to A, we must have

X ⊥ A ⇐⇒ XA = 0.

Algebraically, when you write out X and A in their factors, the common parts of X and

A produce a scalar, and the result then reduces to orthogonality of one of the remaining

factors of X with all the remaining factors of A.

440 CONSTRUCTIONS IN EUCLIDEAN GEOMETRY CHAPTER 15

Suppose we have two blades A, B, and are looking for the Euclidean object X that is

perpendicular to each. We therefore need to satisfy XA = 0 and XB = 0. Dualizing

this we get X ∧ A

∗

= 0 and X ∧B

∗

= 0. By choosing the duality relative to the join of the

two blades A and B, we can make A

∗

and B

∗

to be independent blades, just as we did for

the

meet above. This prevents their outer product from being trivially zero. A blade X of

lowest grade orthogonal to every non-scalar factor in A and B, and hence

X = B

∗

∧ A

∗

where the order was chosen to correspond to the convention for the

meet.

Whereas the

meet constructs a representation of an object in common with given ele-

ments, this operation of plunging (our term) constructs the representation of an object

that is most unlike other elements, in the orthogonal sense that it intersects them per-

pendicularly. We coined the term

plunge (which according to Webster’s dictionary may

be etymologically related to plumb) to give the feeling of this perpendicular dive into its

arguments. Since perpendicularity is a metric concept, the

plunge is a truly metric oper-

ation, whereas the

meet is not. The plunge is an elementary construction in Euclidean

geometry that deserves to be better known. It is occasionally found in older works in the

Grassmannian tradition [9, 22].

With the associativity of the outer product, the

plunge easily extends to more elements, so

that the general element perpendicular to A

, A

, and so on, has the direct representation

X = ···∧A

∗

∧A

∗

.Theplunge of three spheres, as in Figure 15.1(b), is therefore a circle:

X = C

∗

∧ B

∗

∧ A

∗

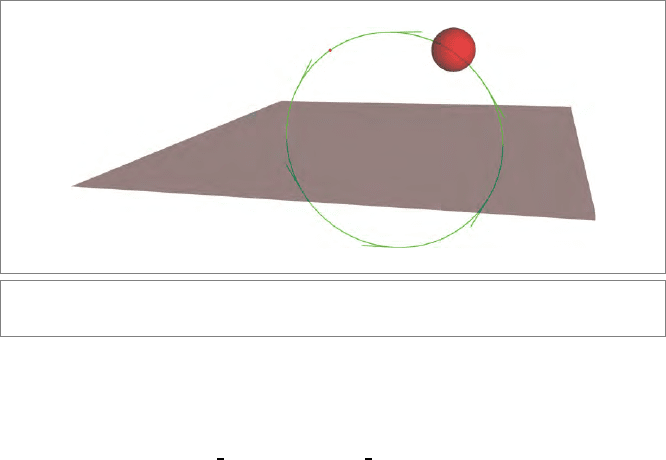
Shrinking the dual spheres to zero radius so that they become points, you see that the

plunge gives a circle through those points, consistent with our earlier derivation of the

interpretation of such an element c ∧b ∧a, with a, b, and c point representatives. We now

see that to contain a point a is equivalent to plunging into the zero-radius sphere a

−∗

that point. Letting the radius of a dual sphere go to inﬁnity gives a dual plane; the

plunge

of such diverse elements can be mixed easily, as Figure 15.2 shows.

15.1.3 REAL MEET OR PLUNGE

The meet and the plunge are clearly each other’s dual relative to the join.Moreover,

should the result of one of them be imaginary, the other is real. This can only happen for

rounds (since ﬂats are always real). That principle helps with ﬁnding and visualizing an

imaginary

meet.

Take again the three spheres of Figure 15.1(b). They do not intersect and therefore have

an imaginary point pair as their

meet. This implies that their plunge is a real circle. This

imaginary point pair and the real circle are algebraically each other’s dual. Geometrically,

this duality is a polar relationship on the unique smallest sphere containing either point

SECTION 15.1 EUCLIDEAN INCIDENCE AND COINCIDENCE 441

Figure 15.2: The plunge c ∧ b ∧ a of dual plane c, dual sphere b, and point a.

pair or circle (or both, since they are on the same sphere). This is easily shown from the

standard representation of such rounds:



(o +

∞) E



∗

= (o −

∞) E

夹

(−1)

If the former is a real circle on the sphere with squared radius ρ

> 0, then E is of grade

2; in a 3-D Euclidean space the latter is then a point pair on the imaginary sphere of the

same radius (since E

夹

is of grade 1). That locates the imaginary meet.

If a circle is considered as the real equator of a sphere, its dual is the imaginary point

pair that form the poles. Vice versa, the dual of a real point pair is the imaginary

equator of a sphere that has the point pair as its poles.

Knowing this polar relationship of

meet and plunge, we can also determine the location

of the imaginary circle that is the

meet of two nonintersecting spheres, as indicated in

Figure 15.3(a). The

plunge of the two spheres is a point pair (indicated in blue). The loca-

tion of this point pair is found by realizing that any sphere that is perpendicular to both

spheres should contain it (since the

plunge is an associative operation), and so should

every circle, plane, or line perpendicular to both spheres. The simplest way to localize

it is then as the intersection of the line through the centers (which is clearly perpendic-

ular to both spheres) and the unique perpendicular sphere with its center on this line,

as indicated in Figure 15.3(a) (in white). That is precisely the sphere on which we should

determine the

meet as the dual to this point pair, which is the imaginary equator indicated

as a dashed circle in Figure 15.3(a) (in green). We will give the formula for this sphere in

Section 15.2.3.

Once you know how to ﬁnd this round that contains both

meet and plunge, their

visualization is easy, whether they are imaginary or not. Verify that this indeed gives the

localization of both in Figure 15.3.