Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

412 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

14.3.2 CIRCLE REPRESENTATION

Let us ﬁnd out what another representative vector σ on this tangent plane represents in the

Euclidean base space. We can construct it from a point C in the Euclidean space, making a

vertical line c∧∞out of its representative c, and intersect that with the tangent plane. That

gives a representation point σ = x(c ∧∞). We have met this element σ as representing

a dual circle through the point x with center c. Let us ﬁnd out why this is the correct

interpretation in this visualization as well. The position of σ relative to x is sketched in

Figure 14.4. Since σ is on the plane with dual representation x, we must have σ · x = 0.

But this also implies that x · σ = 0, which we would interpret as x being on the plane

dually represented by σ. What is this dual plane of σ, and what other point representatives

are on it? All such points y must satisfy y · σ = 0, and therefore σ · y = 0. So all these

points must be such that σ lies on their tangent plane; that must imply that they are the

contour of the parabola as seen from σ. Together, they lie on the plane dually represented

by σ, which therefore passes through the parabola in the way indicated in Figure 14.4.

That is then a geometrical way of constructing the dual of σ: as the connecting plane of

tangent points to the paraboloid as seen from σ. In projective geometry, this construction

is known as determining the polar of σ relative to the paraboloid. When you project down

the resulting ellipse, you ﬁnd a circle of Euclidean points, so the plane dual to σ is the direct

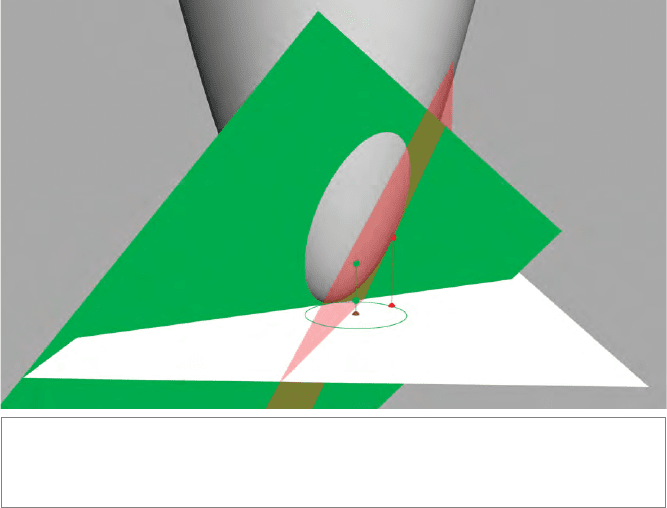
Figure 14.4: The representation of a circle through the point X is by a conformal point σ on

the tangent plane of x. The plane dually represented by

σ cuts the paraboloid in the represen-

tations of the points on the Euclidean circle.

SECTION 14.3 A VISUAL EXPLANATION OF ROUNDS AS BLADES 413

representation of a circle. We show a cross section of this situation in Figure 14.5 for clarity

(alternatively, you can see this as a depiction of the conformal model of a 1-D space).

A circle is represented by a plane that cuts the paraboloid in an ellipse, which projects

down to a circle in the Euclidean space.

The position of the plane relative to the point σ can be understood as follows. Since

σ = x(c ∧∞) = (x · c) ∞ + c,wehaveσ

= −2(x · c), so that σ can be written as

σ = c −

∞. Therefore, the point σ is a distance of

under the paraboloid at c.

When we look for the intersections with a vertical line x ∧∞at any location x with

both the plane dually represented by σ and the tangent plane at c, we ﬁnd that these are

x·(c−

∞) = x·c+

and x·c, respectively. This shows that the dual plane σ is parallel

to and above the tangent plane at c, by an amount of

in the ∞-direction. So the dual

plane σ is as far above the paraboloid as σ is below it. This computation of the relative

position of σ and its dual plane σ holds independently of the value of σ

. If it is positive,

we have the construction depicted in Figure 14.4; if it is zero, we have the dual plane of a

point, which is the tangent plane depicted in Figure 14.3; and if it is negative, the point σ

is above the paraboloid, and the dual plane σ below it, still parallel to the tangent plane.

Thus we ﬁnd a sensible real construction of the dual of an imaginary circle.

∗

Figure 14.5: Cross section of the parabola of null vectors. On the right-hand side, a point x

and its dual x

∗

, which is the direct representation of the tangent plane at x. On the left-hand

side, the representation of a dual sphere

σ. Its dual σ

∗

represents a plane as far above the

parabola as

σ is below it. It intersects the parabola in the points representing the sphere in the

base space. These are on the contour of the parabola as seen from

σ.

414 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

14.3.3 EUCLIDEAN CIRCLES INTERSECT AS PLANES

Figure 14.6 shows how to do the intersection of two Euclidean spheres (which in 2-D

are of course circles) in the conformal model. The answer is a Euclidean point pair (i.e., a

0-sphere). We know that the 2-D conformal model would represent this as the outer prod-

uctoftwonullvectorsx ∧ y. That is represented as a line in this homogeneous depiction

of the representational space, intersecting the paraboloid at the two representatives of the

points x and y.

The ﬁgure shows clearly that this line representing the intersection of the two circles is the

intersection of the two planes representing the circles. Those planes are in turn the duals

of the circle representations σ and τ as homogeneous points under the paraboloid.

There is therefore nothing quadratic about intersecting two circles once we are in the

conformal model; it is the same as intersecting planes. If the planes should intersect in

a line that does not pass through the parabola, we would interpret this as an imaginary

Figure14.6: Visualization of the intersection of circles in the conformal model. The red circle

in the 2-D Euclidean base space is represented by the red plane, and dually represented by

the representative vector

τ. The green circle is similarly represented by the green plane and

the vector

σ. The intersection of the two circles is the blue point pair, which is represented

by the blue line (

σ ∧ τ)

−∗

, the intersection of the two planes. The dual of that line is the yellow

line

σ ∧ τ connecting the dual circle representatives.

SECTION 14.4 APPLICATION: VORONOI DIAGRAMS 415

point pair (it is a nice puzzle to construct its location), but there is nothing irregular about

the intersection itself. Here is the take-home message of all this visualization:

In the confor mal model of a 2-D Euclidean space, intersecting circles is identical to

intersecting offset planes in a space of one more dimension (the ∞-dimension). In

yet one more dimension (the o-dimension), this is identical to inters ecting subspaces

through the origin. Therefore, the

meet of origin blades in the conformal model is

effectively circle intersection.

We hope this visualization helps you understand slightly better where those two extra

dimensions come from, and why ﬂat elements through the origin of the representational

space

n+1,1

(its blades) can represent round elements in the Euclidean space E

14.4 APPLICATION: VORONOI DIAGRAMS

The Voronoi diagram of a set of points is a graph that partitions space into the parts closest

to each of them, as in the base plane in Figure 14.7. In computational geometry literature

[12], an interesting construction is made that turns the computation of a Voronoi diagram

of a set of points into computing a convex hull of a properly constructed polyhedron in

a space of one more dimension, projected down. The polyhedron is made up of parts of

tangent planes of lifts of the original points to a paraboloid set up in the extra dimension.

This paraboloid construction is usually presented as a special clever trick, and not used

in other algorithms. We will show that it is essentially the conformal model, and there-

fore much more widely applicable than is usually appreciated. Let us analyze the Voronoi

construction in more detail, making full use of the convenient metric that the conformal

model dictates for the extension of the Euclidean base space

to R

n+1,1

We have just seen how points are mapped to the paraboloid in the conformal model

construction and how we can use a homogeneous model in the resulting space to con-

sider the tangent planes. Now consider two points P and Q of the Euclidean base space,

lifted to the paraboloid as p and q. If we want to determine which points are closer to

one than the other, the separation line between those is the perpendicular bisector, which

is the line dually represented as p−q in the conformal model. In the paraboloid represen-

tation, this line can be made by intersecting the tangent planes to p and q. We show this

in two steps: ﬁrst, since the tangent planes are dually represented by p and q, their

meet

is Λ=(p ∧ q)

−∗

. To ﬁnd what this line in our model represents, we need to turn it into

a plane stretching to inﬁnity, and intersect that with the 2-D Euclidean base space. The

plane is ∞∧Λ=∞∧(p ∧ q)

−∗

= (∞(p ∧ q))

−∗

= (p − q)

−∗

. The intersection with the

base plane gives (p − q)(o ∧ I

∧∞) = (p − q)

−∗

, consistent with our assumption that

this line was dually represented by p − q.

These perpendicular bisectors of point connections are the carriers of potential edges of

the Voronoi diagrams in

. We still need to select those among them that are actually

416 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

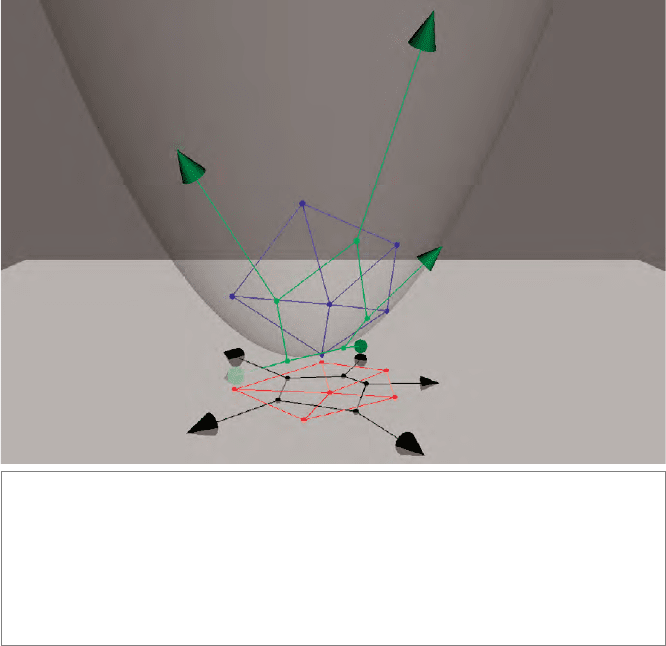
Figure 14.7: The Voronoi diagram of six red points in a 2-D Euclidean space is indicated in

black, and their Delaunay triangulation in red. In the conformal model, the represented Delau-

nay triangulation (in blue) is obtained by making the convex hull of the represented points on

the paraboloid, which is the ﬁve-sided pyramid. The representation of the Voronoi diagram is

its dual in the conformal model, depicted in green, which is a planar pentagon with ﬁve rays

(indicated by tangent vectors). The green points are below the paraboloid. They are the repre-

sentations of the circumcircles of triangles, whose centers are the corresponding black points

of the Voronoi diagram.

closest to the given points not overruled by other bisectors of even closer points. When

we study this by entering a third point R, we have to decide among the bisectors dually

represented as p − q, q − r, and r − p. These are lines in the intersection of the three

tangent planes dually represented by p, q, and r, and they intersect in a single point in

the representational space. This point is dually represented by p ∧ q ∧ r, and it represents

the circumcircle of p, q, and r. Its projected location in the base space is the center of the

circumcircle. It is clear that the parts of the bisectors that show up in the Voronoi diagram

are the lines that are highest in the ∞-direction of the representation.

This holds for each triplet of points: the representations of the Voronoi lines connect

the intersection points of each triplet of tangent planes, in the highest possible manner.

Therefore we can determine the Voronoi diagram by constructing all such lines and deter-

mining their upper convex hull in the ∞-direction. It is illustrated as the green network

SECTION 14.5 APPLICATION: FITTING A SPHERE TO POINTS 417

in Figure 14.7, which projects down to the black Voronoi diagram in the 2-D Euclidean

base space.

Using the principle of duality, this construction can be improved and made much more

direct, for the intersection line (p ∧ q)

−∗

of a tangent plane of point representatives p and q

is exactly dual to the connection line p∧q between the point representatives. When we take

the dual of the complete network of line segments representing the Voronoi diagram, this

generates a network that forms the convex hull of the point representatives themselves.

It is illustrated as the blue network in Figure 14.7. It is in fact the representation of the

Delaunay triangulation of the point set. That is the network of which the edges denote the

closest point connections, indicated in red in Figure 14.7.

So the Delaunay triangulation of a set of points can be determined by lifting them all to

a paraboloid, taking their convex hull, and projecting back. The corresponding Voronoi

diagram is obtained from this by duality. That is precisely the convex hull algorithm from

[12]. We have shown that this is actually a hidden application of the conformal model.

You can play around with this algorithm in the programming example of Section 14.9.1.

14.5 APPLICATION: FITTING A SPHERE TO POINTS

14.5.1 THE INNER PRODUCT DISTANCE OF SPHERES

The inner product of the conformal model was deﬁned to give a good correspondence

to the squared Euclidean distance of normalized points in

represented as vectors in

n+1,1

. Meanwhile, we have found that vectors of R

n+1,1

can also represent dual spheres

(and planes) of

. We investigate what distance measure between spheres is deﬁned by

the inner product of vectors.

When we have two dual spheres σ

= c

−

∞and σ

= c

−

∞, their inner product

· σ

= c

· c

(ρ

+ ρ

) =



+ ρ

− d

)



where d

) is the square of the Euclidean distance of their centers.

Figure 14.8 shows some situations for the geometry of the inner product. Let us ﬁrst

assume that one of the spheres is a point. In that case we ﬁnd two situations, depending on

whether the point is inside or outside the other sphere. If it is outside, as in Figure 14.8(a),

the inner product denotes minus half the tangential distance of the point to the sphere,

since its value becomes

σ · p = −



(C,P) − ρ



When the point is inside, the interpretation as a real distance changes to Figure 14.8(b).

It is interesting to see what happens when the point gets close to the sphere at a distance

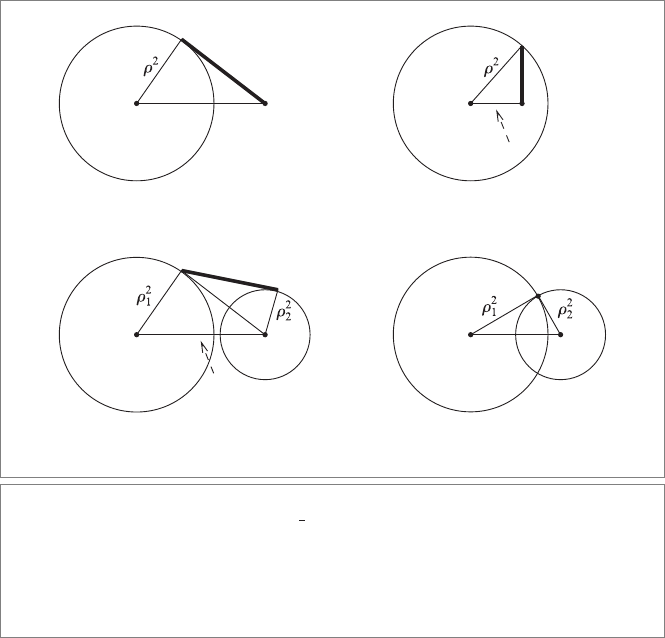
418 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

(a)

−2c

−2σ

(b)

−2c

2σ

(d)

−2c

−2σ

(c)

Figure14.8: The inner product σ

·σ



+ ρ

−d

)



can be interpreted as a squared

distance measure between spheres. In the ﬁgure all distances are real and denoted by their

squares. (a) When σ

is an outside point p , it is minus half the squared length of the tangent

line segment from p to σ. (b) When σ

is an inside point p, it is half the squared length of the

perpendicular arc from p to σ. (c) For two spheres, the construction is more involved. (d) The

distance is zero when the two spheres intersect perpendicularly.

ρ + δ from the center: then the inner product is equal to −ρδ,toﬁrstorderinδ. That

implies that for points close to the sphere, it is linearly proportional to their distance to

the sphere. This is a useful distance measure in optimization problems involving spheres,

and we use it for sphere ﬁtting in the next section.

For the general case of two spheres, the quantity representing the inner product can be

constructed by a nested tangent construction, as illustrated in Figure 14.8(c). This does

not immediately convey its usefulness. But Figure 14.8(d) shows an interesting special

case: when the inner product of two spheres is zero, they intersect orthogonally. In this sense,

the inner product of the conformal model is a measure of orthogonality.

By contrast, the outer product of two dual spheres is their dual intersection. When two

spheres touch, this is a tangent element, characterized by having a zero square. So when

the outer product of two spheres has zero norm, they touch.

SECTION 14.5 APPLICATION: FITTING A SPHERE TO POINTS 419

14.5.2 FITTING A SPHERE TO POINTS

The representation of spheres as vectors leads to a simple method to ﬁt the optimal sphere

to a set of points, minimizing the sum of the squared distances (well, almost). This uses

the structure of the conformal model to derive a procedure that can be executed classically.

This section was inspired by [48].

In ﬁtting a sphere to a set of points {p

}

i=1

, we can ask to minimize the sum of the squared

distances. If a point p is at a close distance δ to a dual sphere σ with radius ρ, the inner

product p · σ is −ρδ,toﬁrstorderinδ (see previous section). Therefore for a close point,

the squared distance is (p·σ)

/ρ

= (p·σ)

/σ

= (p·σ)(p·σ

−1

), for a normalized sphere,

σ, for which −∞ · σ = 1.

So as a cost function for the ﬁt we have

Γ ≡



· σ)(p

· σ

−1

We ask for the σ that minimizes this. Differentiating with respect to σ and equating to 0

gives

0 =

∂Γ



∂σ

= 2



· σ)(p

∧ σ)σ

−3

Unfortunately, we do not know how to solve this equation, since it is strongly nonlinear

in σ.

If we change the problem slightly, we can ask for the sphere that minimizes the summed

squares of ρδ rather than δ. This would minimize the distances to the points, but with a

preference for small spheres. In practice, this solution will be close to the one we would

have wanted. In this form it is solvable, for now the cost function is



≡



· σ)(p

· σ),

and optimization of this gives

0 =

∂Γ



∂σ

= 2



· σ).

The single occurrence of σ makes this a linear equation that can be solved using standard

linear algebra techniques, as follows. First, we realize that we can write the conformal

space inner product in terms of a Euclidean inner product by the using metric matrix

[[ M]] , which in 3-D is as given in Table 13.1:

[[ M]] =

⎡

⎢

⎣

⎡

⎢

⎣

0 000−1

0 100 0

0 010 0

0 001 0

−1000 0

⎤

⎥

⎦

⎤

⎥

⎦

420 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

for a conformal model with basis {o, e

, e

, ∞}.Nowp·σ is implemented on the vectors

[[ p]] and [[ σ]] as an expression in the usual linear algebra of a Euclidean space:

p · σ = [[ p]]

[[ M]] [[ σ]] ,

where we should use the vector [[ 1 , p

, p

+ p

)]]

as a representation for

each measured point p. We then need to solve, in least-squares fashion,



[[ p

]] [[ p

]]

[[ M]] [[ σ]] = 0.

To avoid the trivial solution [[ σ]] = 0, we use the scaling freedom in our representation

to demand that σ · σ be constant and equal to 1. The nontrivial least-squares solution is

then found using the standard singular value decomposition of the data matrix

[[ D]] ≡



[[ p

]] [[ p

]]

[[ M]] = [[ U]] [[ Λ]] [[ V]]

The optimal σ is the last column of [[ V]] , which is the eigenvector corresponding to the

smallest singular value. This is proportional to the dual sphere that minimizes Γ



, and you

can compute its center and radius using Table 14.1.

If you truly needed to minimize Γ rather than Γ



, you can use the solution for Γ



as the

seed for a nonlinear optimization method such as Levenberg-Marquardt.

14.6 APPLICATION: KINEMATICS

14.6.1 FORWARD KINEMATICS

In computer animation and robotics, forward kinematics is used to compute the location

and change of geometrical objects given a change in their parameters. As a typical example

of the kind of problem, we treat the forward kinematics of a humanoid arm, in which we

need to compute where the limbs end up, given the angles of the various joints. With

translations and rotations both available as versors, we can now write this in terms of the

conformal model.

In the classical way of doing this, one uses the homogeneous model to compute the rigid

body motion matrices for vectors, as in Table 12.2, and multiplies those to get a transfor-

mation matrices for points on each of the limbs. That chain structure is of course essential

to the problem, and also found in the conformal model solution. The only difference is

that the resulting rigid body motion versors can be applied to elements of any kind, not

just vectors. When all you need to do is to control a robot, this is not that relevant, but if

you want to render an animation of the arm, this is potentially useful. There is no longer

a necessity to decompose the graphic elements of a limb down to the level of vectors or

points; line elements, circles, or tangent bivectors are just as easily transferred and ren-

dered at their proper location on the moved arm.

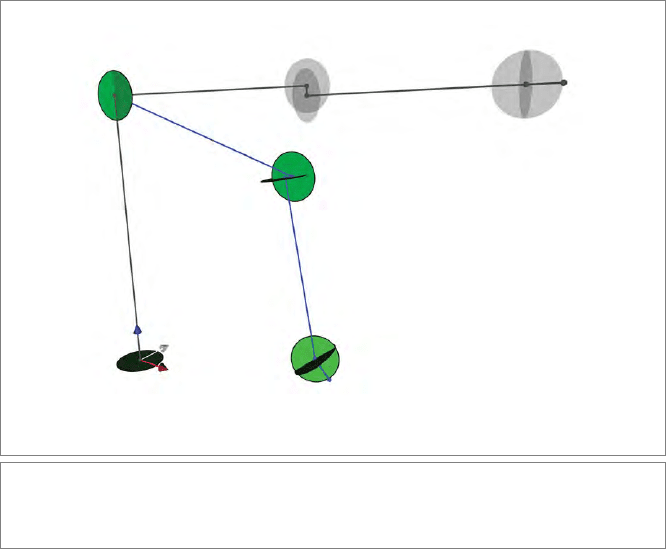
SECTION 14.6 APPLICATION: KINEMATICS 421

To take a speciﬁc example, let us take the structure of a Unimation Puma 560 robot.

We start with the deﬁnition of the robot dimensions and the directions of their rotation

planes from its manual. This gives the essential kinematics structure indicated in gray in

Figure 14.9. It is encoded as translations (in meters) and rotation bivectors as:

= 6.60 e

= e

∧ e

= 4.31 e

+ 1.49 e

= e

∧ e

= −0.20 e

= e

∧ e

= 4.33 e

= e

∧ e

= 0 B

= e

∧ e

= 0.56 e

+ 0.11 e

= e

∧ e

We can introduce a set of graphic elements X

to be drawn for limb i; they can be points,

bivectors, circles, spheres, or whatever you need to draw the limb. You initially specify

them in the coordinate frame of the corresponding limb i. In Figure 14.10, each limb is

drawn by means of the point at its the origin o, the tangent blade of the rotation plane at

the origin indicated as the tangent bivector o ∧ B

, and the point pair o ∧ T

[o] drawn as

a line segment.

Figure 14.9: A Unimation Puma 560 arm, in its home position (gray) and during a motion.

We used connected point pairs and tangent bivectors to denote the limbs. They transform in

the same manner.