Дорожинський О.Л., Тукай Р. Фотограмметрія

Подождите немного. Документ загружается.

Μ-Ν

для к =

О,

1,..., L -1, де L -кількість рівнів сірого; p

(г

) - відносна частота появи

к-то

рівня сірого тону; п

- кількість пікселів

к-то

тону у зображенні. Змінна г

передає нормалізований рівень сірого тону у початковому зображенні, причому

/0=0 відповідає чорному тону, a r

- білому.

Для p

) виконується:

1-Х

Σ/ν(*) =

· (4.30)

к=0

Нормалізована гістограма має очевидну інтерпретацію - це емпірична

щільність ймовірностей значень рівнів сірого тону зображення / . Іншими словами,

якщо піксел з координатами (х,у) розглядається як випадковий, то р

(г

) - це

ймовірність того, що f(x,y) = k і дорівнює

)

{f(x,y)

k}.

Визначимо кумулятивну функцію перетворення як

= (4.31)

Ι=η

І=п

0<г*<1, 0<^<1,

Функція Т(г

)е емпіричною функцією розподілу ймовірностей, отже, це

неспадна функція.

Застосування (4.31) пояснимо на прикладі фрагмента 8-рівневого зображення

з розподілом сірого тону, як показано у табл. 4.2.

160

Таблиця

4.2

Розподіл рівнів сірого нормалізованої та вирівняної гістограм

гк

РЛ

к)

Пг

)

*{L-\)

К =

INT[s

*{L-1)]

»sk Ps(

0 4 0,04

0,04

0,28 0 11

0,11

7 0,07 0,11 0,77

0 0

2 9 0,09 0,20 1,40 1

9 0,09

0,11

0,31 2,17

2 11

0,11

4 14 0,14

0,45 3,15

3 14 0,14

17 0,17 0,62

4,34 4

17 0,17

6 18 0,18

0,80 5,60

5 18 0,18

20 0,20 1,00 7,00 7 20 0,20

Гістограма розподілу відповідних рівнів сірого тону подана на рис. 4.19.

Функція перетворення (4.31) обчислюється у такій послідовності:

= Пг

) = Σ Ρλη)

= Pr(n>) =

°>

;

7=0

=Γ(γ

)=Σλ('>)

= Λ(

ο) + Λ(

ι) =

7=0

=0,20, s

=0,62,

=0,31, s

=0,80,

=0,45, s

= 1,00.

Оскільки у цьому прикладі є тільки 8 дозволених рівнів, то кожному з

перетворених значень можна призначити найближче значення рівня, наприклад,

161

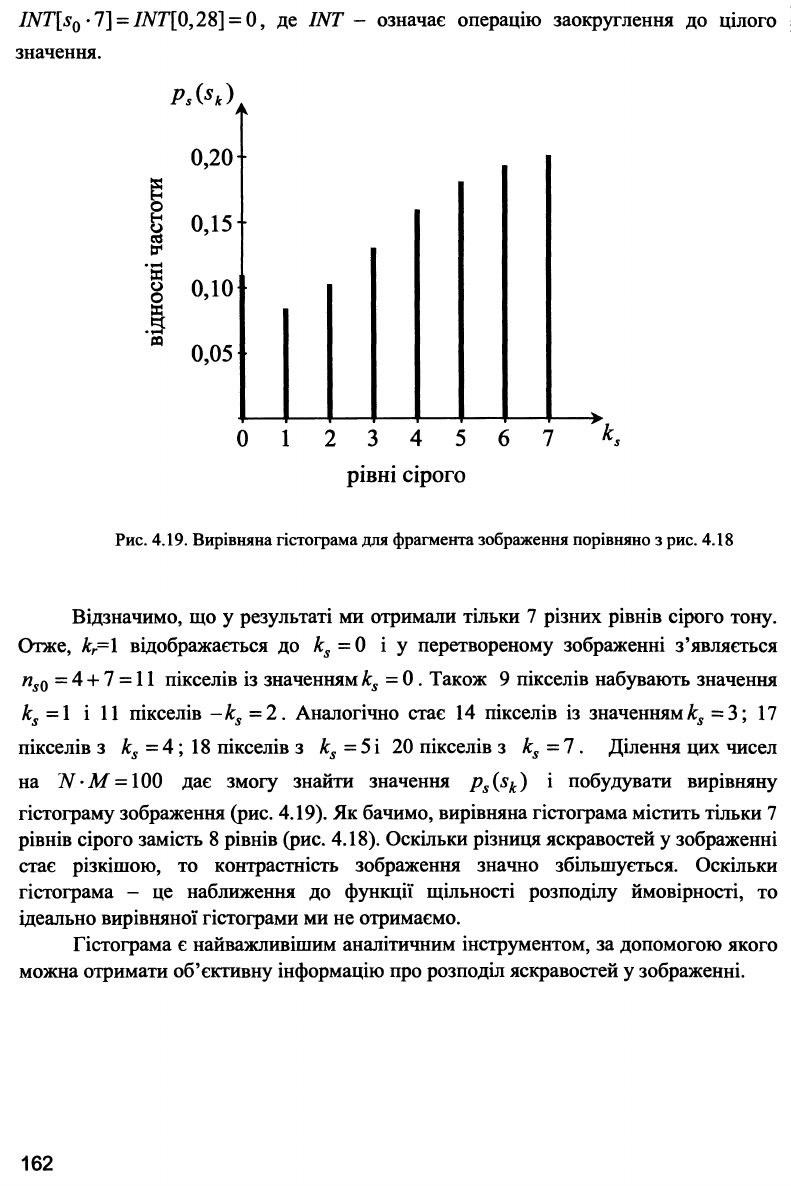
INT[s

7] = ΙΝΤ[0,28] = 0, де INT - означає операцію заокруглення до цілого j

значення.

Ps(s

)

0,20 ·

0,15-

0,10

0,05

01234567 Κ

рівні сірого

Рис. 4.19. Вирівняна гістограма для фрагмента зображення порівняно з рис. 4.18

Відзначимо, що у результаті ми отримали тільки 7 різних рівнів сірого тону.

Отже, к

= 1 відображається до k

= 0 і у перетвореному зображенні з'являється

=4 + 7 =

пікселів із значенням k

= 0. Також 9 пікселів набувають значення

=1 і 11 пікселів -k

-2. Аналогічно стає 14 пікселів із значенням^ = 3; 17

пікселів з k

= 4; 18 пікселів з k

і 20 пікселів з k

= 7 . Ділення цих чисел

на N-M = 100 дає змогу знайти значення p

) і побудувати вирівняну

гістограму зображення (рис. 4.19). Як бачимо, вирівняна гістограма містить тільки 7

рівнів сірого замість 8 рівнів (рис. 4.18). Оскільки різниця яскравостей у зображенні

стає різкішою, то контрастність зображення значно збільшується. Оскільки

гістограма - це наближення до функції щільності розподілу ймовірності, то

ідеально вирівняної гістограми ми не отримаємо.

Гістограма є найважливішим аналітичним інструментом, за допомогою якого

можна отримати об'єктивну інформацію про розподіл яскравостей у зображенні.

СҐ

• і-Ч

162

4.5.4. Згладжування зображень

Операції згладжування використовують переважно для зменшення шуму або

ефекту муару, який виникає у цифровому зображенні у результаті недостатньої

вибірки або квантування.

Осереднення околу

Осереднення околу належить до методу просторової області для

згладжування зображення. Для заданого NxN зображення f{x,y) операція

побудови згладженого зображення g{x,y) полягає у визначенні середнього

значення пікселів в околі кожної точки

(х,у).

Згладжене зображення отримують за

співвідношенням

>y)

77 Σ /М (4·

)

(n,m)eS

Для х,у - Ο,Ι,.,.,Ν-I S- множина координат точок в околі точки(jc,j;),

включаючи її саму. Μ - загальна кількість точок в околі.

Рис. 4.20. Згладжування зображення методом осереднення околу: а

—

початкове зашумлене

зображення; б, в

—

результат оброблення за формулою (4.26) з околами розмірів 9x9 та 31x31

На рис. 4.20 показано ефект згладжування з використанням методу

осереднення околу. На рис. 4.20, а бачимо чотирирівневе зображення, пошкоджене

шумом. Рис. 4.20, б, в є результатом згладжування зашумленого зображення з

околами η =9, 31 відповідно. Як бачимо, ступінь згладжування пропорційний до

розміру вибраного околу.

Ефект згладжування може бути зменшений використанням порогового

критерію. Замість використання (4.32) утворюємо g(x

y)· за таким правилом:

163

g(x,y) =

якщо

(n,m)eS

1V±

(n,m)eS

(JC,

у) у протилежному випадку

<Т

(4.33)

де Γ - порогове значення. Такий підхід залишає без зміни області зображення з

великим, порівняно з Τ, відхиленням рівнів сірого тону. Можна очікувати, що

більші відхилення відповідають контурам, тому використання умови (4.33) приведе

до зменшення нечіткості контурів.

Рис. 4.21. Зображення рис. 4.20,

згладжене за (4.33)

з використанням околу 9x9 та 7М0

Порівняння цього результату з рис. 4.20 показує, що межі між чотирма

квадратами є різкішими на рис. 4.21.

Медіанна фільтрація

Основні недоліки методу згладжування полягають у тому, що розпливаються

контури та інші чіткі деталі. Хоча цю проблему можна обійти використанням

порогу, але вибір порогового значення пов'язаний зі значними випробуваннями.

Альтернативний підхід полягає у застосуванні медіанного фільтра, за якого середнє

значення сірого тону кожного піксела заміняється медіанним значенням із рівнів

сірого в околі кожного піксела. Цей метод особливо ефективний, якщо характер

шуму зумовлюють окремі яскраві (темні) точки і якщо треба зберегти чіткі

контури.

Нагадаємо, що медіаною т множини значень є таке значення, що половина

значень множини менша, ніж т, а половина більша, ніж т. Для виконання

медіанної фільтрації в околі піксела спочатку впорядковують за зростанням

значення сірого тону в цьому пікселі та його сусідах, далі визначають медіану і

призначають це значення пікселу. Припустимо, що окіл 3x3 складається із значень

(10, 25, 25, 19, 150, 19, 19, 25, 25). Впорядковуємо ці значення як (10, 19, 19, 19, 25,

25, 25, 25, 150) і визначаємо медіану - 25.

Як бачимо, механізм медіанної фільтрації полягає в тому, що точки з

екстремальними значеннями яскравості після сортування стають крайніми у

164

послідовності, медіана має значення, подібне до сусідніх пікселів. У такий спосіб

усуваються яскраві (темні) ізольовані піксели в околі. Перевага методу медіанної

фільтрації порівняно з методом осереднення околу полягає у можливості

виконувати два або більше проходів для усунення точкового шуму.

Визначення країв між областями

Для визначення країв між областями на зображенні найпоширенішим є

градієнтний метод. Край - це границя між двома областями з порівняно різними

властивостями сірого тону. Для заданої функції А

У) градієнт / від координат (х,у)

визначається як вектор

З векторного аналізу відомо, що вектор вказує у напрямку максимальної

швидкості зміни /у точці (χ,γ). Для визначення країв між областями на зображенні

нас цікавить модуль вектора, який позначається

G[f(x,y)],

причому

4.5.5. Підкреслення країв у зображенні

G[f(x

y)]=

(4.34)

(4.35)

Ця величина дорівнює максимальній швидкості зростання f(x,y) у напрямку G.

На практиці градієнт наближають сумою абсолютних значень похідних:

(4.36)

Таке наближення значно легше реалізувати.

Маски обчислюють за формулами

(4.37)

де г має зміст, який пояснено у (4.12).

Ці дві маски називають операторами Собеля (рис. 4.22).

165

-1 -2 -1

0 0 0

2 1

-1

0 1

-2 0 2

-1

Рис. 4.22. Оператори Собеля; а

—

для обчислення G

—

для обчислення G

Щоб отримати градієнт, використовують комбінацію (4.35) або (4.36).

Згортання цих масок із зображенням f(x,y) дає градієнт в усіх точках зображення і

його називають градієнтним зображенням. Існують багато способів побудови

градієнтного зображення з використанням порогових значень. Нижче наведено

можливі варіанти побудови градієнтних зображень:

а) підсилення важливих країв із збереженням особливостей гладкого фону:

g(*,y)=<

G[f(x,y)\І, якщо G[f(x,y)]>T,

f(x,y), у протилежному випадку;

(4.38)

б) задавання країв певним рівнем сірого кольору, а фон залишається без

зміни:

g(x,y)

= <

\ L

, якщо G[f(x,y)]>T,

[f(x,

у), у протилежному випадку,

де L

- рівень сірого тону для країв;

(4.39)

в) вивчення зміни сірого тону країв без впливу фону:

, ч \G[f(x,y)l якщо G[f(x,y)]>T,

g(x,y)

(4.40)

в>

у протилежному випадку,

- рівень сірого тону для фону;

г) побудова бінарного градієнтного зображення, де краї і фон зображені

двома різними сірими тонами:

g(x,y)=<

, якщо G[f(x,y)]>T,

, у протилежному випадку,

(4.41)

J&L

- рівень сірого тону для країв, a L

- рівень сірого тону для фону, Τ -

порогове значення, яке підбирають експериментально.

166

Визначення належності піксела темній чи світлій стороні

краю

Для цього використовують оператор Лапласа:

2 2

+ (4-42)

ох ду

який наближено можна обчислити згортанням маски (рис. 4.23) із зображенням

f(x,y). Якщо вектор сформований із коефіцієнтів цієї маски, ми можемо виразити

оператор Лапласа (лапласіан) у формі:

L[f(x,y)]

-r, (4.43)

де г має зміст, який пояснено у (4.12).

0 1

-1

-4

0 1

Рис. 4.23. Маска

для обчислення

оператора Лапласа

Зауважимо, що лапласіан дорівнює нулю на постійних областях сірого тону і

на похилих частинах країв, як і очікується від похідної другого порядку. Він реагує

на зміну інтенсивності сірого тону, але рідко використовується для самого

виявлення країв. Причина в тому, що оператор другої похідної є занадто чутливим

до шуму. Тому цей оператор відіграє другорядну роль детектора для встановлення

належності цього піксела темній або світлій стороні краю.

4.5.6. Поліпшення зображень за допомогою частотних фільтрів

Завдання поліпшення зображення полягає у виборі передавальної функції

H(u,v)

g(x,y) = З"

[Щи, ν

/(и, ν)] (4.44)

у такий спосіб, щоб отримане зображення мало певні характеристики (де З

-1

[...]

означає обернене перетворення Фур'є (ОПФ) виразу у квадратних дужках).

Як відомо, краї між областями однорідного сірого тону та інші різкі перепади

яскравостей (такі, як шум) становлять значну частину високочастотних компонент

перетворення Фур'є (ПФ). Звідси випливає, що розпливчастість прямо залежить від

високочастотних компонент у прямому перетворенні цього зображення, тоді

167

обернене перетворення дає згладжене зображення. Навпаки, якщо послабити

низькочастотну компоненту перетворення Фур'є, не зачіпаючи високочастотну, то

можна підсилити різкість зображення.

Наведемо приклади передавальних функцій радіально-симетричних фільтрів

низьких та високих частот. Нагадаємо, що назва фільтра збігається з назвою тих

частот, які він пропускає. Передавальні функції, які ми розглянемо, мають однакові

дійсні та уявні частини та нульовий фазовий зсув.

Для згладжування зображень використовують такі фільтри.

Ідеальний Фільтр низьких частот

Двовимірний радіально-симетричний ідеальний низькочастотний фільтр

задається передавальною функцією:

Гі,

якщо D(u,v)<D

H(u,v)

= <

[0, якщо D(u,v)>D

(4.45)

де£>

> 0- константа, а саме радіус кола перемикання частот, a D(u,v)

від центра частотної області до точки з координатами (и, ν) :

відстань

(4.46)

ν)

Рис. 4.24. Вигляд ідеального радіально-симетричного низькочастотного фільтра:

а - зображення маски фільтра: чорні піксели набувають значення 1, а білі - 0;

б - поперечний переріз передавальної функції фільтра

Як випливає із теореми зсуву, для того щоб початок дискретного

перетворення Фур'є функції f(x

y) перенести у центр NxN частотного квадрата,

168

необхідно перетворення Фур'є застосувати до добутку f{x

y) на (-ї)

х+у

(Уразі

одновимірної функції/(х) множимо на (-1)*).

Назва "ідеальний фільтр" виникає з умови, що всі частоти всередині кола

радіуса D

проходять без змін, а всі частоти ззовні цього кола повністю

знищуються. Наведені тут фільтри є радіальносиметричними відносно початку

координат. Зазначимо, що для радіальносиметричного фільтра з центром у

частотному NxN квадраті прийнято, що початок перетворення Фур'є

розташований у центрі квадрата.

Для фільтрів подібного типу достатньо задати поперечний розріз, який

поширюється як функція відстані від початку координат вздовж радіальної

прямої.

Точку

переходу між значеннями H(u,v)

= 1

і H{u,v) - 0 часто називають точкою

перемикання частоти (тут D

). Коли поперечний розріз обертається навколо початку,

точка D

описує коло і ми отримуємо геометричне місце точок перемикання частот на

відстані D

від початку. Величина D

є важливою характеристикою фільтрів і слугує

для порівняння поведінки фільтрів різних типів. Якщо радіус фільтра D

збільшується,

ступінь розпливчастості зменшується і навпаки.

Різке перемикання частот ідеального фільтра не може бути реалізоване за

допомогою апаратних засобів, але може бути змодельоване на комп'ютері.

Фільтр Баттерворта низьких частот

Передавальна функція радіально-симетричного фільтра низьких частот п-го

порядку визначається співвідношенням:

H(u,v) =

(4.47)

де D

, D(u,v) має такий самий зміст, як у (4.45)

H{u,v)

0,5

Рис. 4.25. Поперечний переріз

передавальної

функції низькочастотного фільтра

Баттерворта

169