Додонов А.Г., Ландэ Д.В. Живучесть информационных систем

Подождите немного. Документ загружается.

3.4. Живучесть системы с разветвленной структурой

101

где

— максимально допустимое количество неработоспособных

веток (количество работоспособных веток не меньше, чем

0 0

N i



Допустим, что многократному воздействию подвергается

-ярусная структура с коэффициентами разветвления на ярусах

1 2

, ,..., .

r r r

В рамках данной модели предполагается, что в область действия

точечных НВ попадают только узлы системы, и нарушения работо-

способности различных узлов одного яруса — равновероятные. По-

скольку общее количество узлов в системе составляет

1 1 2

1 ...

r r r

  

1 2

...

r r r

 , можно записать такое выражение:

0 1 1 2 1 2 1 2

... ... 1

k k

r r r r r r

   

    

где



— вероятность нарушения работоспособности узла

-го ранга

после одноразового НВ. Возможны различные гипотезы об уязвимо-

сти элементов, которые учитывают особенности узлов различных ран-

гов, в частности, возможна такая гипотеза, что

1 1 2 1 2

(1 ... ... ) .

i k

r r r r r r

 



     

Тогда, исходя из гипотезы о «равномерности» ярусов, получаем

1 2

1 1

, 1; .

( 1) ... 1

k r r r k

 

  

 

В более общем случае может выполняться

,0 1, 1.

i i i i

a i k a

 



    

Тогда получаем

1 1

, ... , 0 1,

k i i i k

a a a i k

   

 

    

0 1

k k n

i j

n i n j

a r





  

 



 

 

 

3. Сложные информационные сети

102

3.5. Моделирование деструктивного

воздействия на сети

Как и сеть террористов, восстановление которой после деструк-

тивного воздействия описано в [3], информационная система также

является динамической системой, восстановление которой после

уничтожения лучших «посредников» осуществляется за счет латент-

ных связей с другими компонентами информационного пространства.

После того как информационная система разделяется на изолирован-

ные фрагменты, она может «использовать» эти связи и быстро восста-

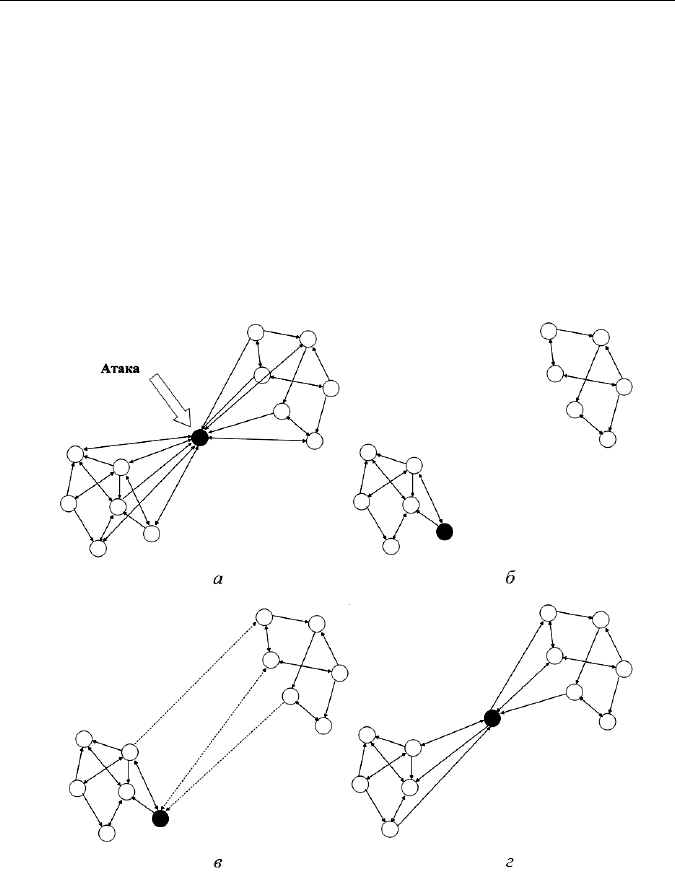
новить связность (рис. 13).

Рис. 13. Восстановление структуры сети путем выбора нового

«посредника»: а — атака на сеть; б — несвязная сеть с изъятым

посредником; в — возрождение скрытых (латентных) связей;

г — связность сети восстановлена

3.5. Моделирование деструктивного воздействия на сети

103

Воссоединение частей сети не состоится, если ни одна из пар

уцелевших после деструктивного воздействия компонент не сможет

найти скрытые связи между собой (возможно, не прямые, а через дру-

гие компоненты информационного пространства). В этом случае

влияние разъединения на показатели функционирования информаци-

онной системы зависит от того, смогут ли снова разъединенные части

получить взаимные связи, недостаток которых наблюдается в этой

части информационной системы.

Если часть информационной системы была близкой к самодос-

таточности, то она продолжает функционировать самостоятельно. В

противном случае она прекращает функционирование до тех пор, пока

не сформируется новая связь. Если одно из соединений оказывается

успешным, то его инициатор становится новым «посредником», кото-

рый объединяет две части сети.

104

4. КРИТИЧЕСКИЙ УРОВЕНЬ

ЖИВУЧЕСТИ СИСТЕМ

Если в сети слишком мало ребер, т.е. средняя степень ее вершин

достаточно мала, то в ней присутствует много изолированных узлов и

кластеров из немногочисленных узлов. При добавлении ребер в такую

сеть (например, установление новых связей, цитирование и т.п.) не-

большие кластеры объединяются в большие.

По достижении некоторого критического уровня, характери-

зующего порог протекания сети, большая часть вершин будет объеди-

нена в кластер, размер которого сопоставим с количеством узлов сети,

т.е. вся сеть станет проводящей.

Этот эффект — фазовый переход — описывается в литературе

как «появление гигантского кластера» [58].

При исследовании живучести сетевой структуры основной ин-

терес представляет противоположный эффект — переход от гигант-

ского кластера к разреженной сети в результате деструктивных воз-

действий, выражающихся в удалении элементов сети — ребер (или

узлов). При этом функциональный отказ рассматривается как уда-

ление отдельного элемента. В этом случае возникает достаточно точ-

ная аналогия с известным в теории перколяции пределом протекания

(или перколяционным порогом), который связывается с фазовым пе-

реходом.

Существующие математические модели такого поведения сете-

вых структур (диодных сетей, сетей террористов и т.п.) при деструк-

тивном воздействии приводятся к перколляционной задаче [59–61].

Как правило, в рамках этой задачи рассматривается решетка из N про-

водящих элементов, после чего рассчитывается проводимость всей

решетки при удалении отдельных ее элементов. Порог проводимости

рассматривается как аналог порога живучести.

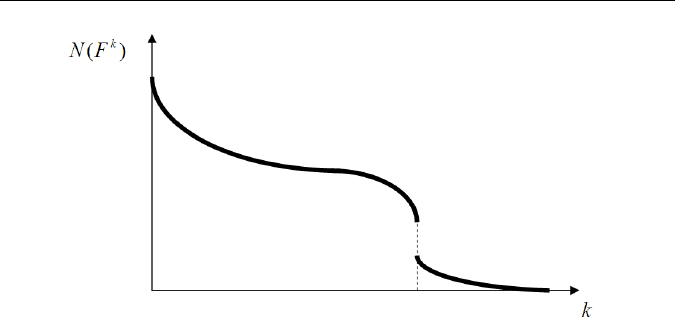
На рис. 14 показан пример типичного поведения подобных мо-

делей. С увеличением количества функциональных отказов

наблю-

дается спад количества выполняемых функций. В общем случае в точ-

ке, которую назовем «критический уровень живучести», происходит

резкий спад (фазовый переход II рода).

4.1. Фазовые переходы

105

Рис. 14. Зависимость количества выполняемых функций

(вертикальная ось) от количества функциональных отказов k

(числа элементов, вышедших из строя)

4.1. Фазовые переходы

Понятие фаз встречается во множестве явлений, приведем не-

сколько примеров. Для воды известно три фазы: жидкая, твердая (лед)

и газообразная (пар). Каждая из них характеризуется своими значе-

ниями параметров. Существенно то, что при изменении внешних ус-

ловий одна фаза (лед) переходит в другую (жидкость). Еще один объ-

ект — ферромагнетик (например, железо или никель). При низких

температурах

360 C

t T

  

никель является ферромагнетиком, при

снятии внешнего магнитного поля он остается намагниченным. При

температуре выше

это свойство теряется, при выключении внеш-

него магнитного поля он переходит в парамагнитное состояние. Здесь,

как и в предыдущем примере, четко видно существование разных фаз

— парамагнитной и ферромагнитной. При изменении температуры

происходит фазовый переход.

В [60] приведен пример из теории перколяции. Случайно выре-

зая из сетки ребра, в конце концов, когда концентрация оставшихся

ребер

станет меньше некоторого значения

, по решетке уже

нельзя будет пройти «из конца в конец». Таким образом, сетка из фа-

зы «протекания» перейдет в состояние фазы «непротекания».

4. Критический уровень живучести систем

106

Из этих примеров ясно, что для каждой из рассмотренных сис-

тем существует так называемый параметр порядка, определяющий, в

какой из фаз находится система. В ферромагнетизме параметр порядка

— намагниченность в нулевом внешнем поле, в теории перколяции —

связность сетки.

Фазовые переходы бывают нескольких типов. Фазовый переход

I рода характеризуется тем, что в системе может одновременно суще-

ствовать несколько фаз. Например, при температуре 0 °С лед плавает

в воде. Если система находится в термодинамическом равновесии (нет

привода и отвода тепла), то лед не тает и не нарастает. Для фазовых

переходов II рода существование одновременно нескольких состояний

невозможно. Сетка со случайно вырезанными ребрами либо связная,

либо нет.

Решающим в создании теории фазовых переходов II рода, нача-

ло которой положил Л.Д. Ландау, было введение параметра порядка



как отличительного признака фазы системы. В одной из фаз, на-

пример парамагнитной,





, а в другой, ферромагнитной,





Для магнитных явлений параметр порядка



— это намагниченность

системы.

Для описания фазовых переходов вводится некоторая функция

параметров, определяющих состояние системы —

( , ,...)

G T



. В фи-

зических системах это энергия Гиббса. В каждом явлении (перколя-

ция, сеть «малых миров» и т.д.) эта функция определятся по-своему.

Главное свойство указанной функции, первое предположение

Л.Д. Ландау — в состоянии равновесия эта функция принимает мини-

мальное значение:

0, 0.

G G

 

 

 

 

В физических системах говорят о термодинамическом равнове-

сии, в теории сложных сетей можно говорить об устойчивости. Заме-

тим, что условие минимальности определяется варьированием пара-

метра порядка.

4.2. Задача теории перколяции

107

4.2. Задача теории перколяции

Одной из важных характеристик сложных сетей является воз-

можность протекания по их ребрам тока, жидкости, информации

(трафика) и т.п. Впервые задача перколяции (англ. percolation — про-

сачивание, протекание) была сформулирована в 1957 г. в работе С.Р.

Бродбента (S.R. Broadbent) и Дж.М. Хаммерсли (J.M. Hammersley)

[61]. В последствии была развита целая область исследований, на-

званная теорией перколяции, имеющая многочисленные применения

на практике. Оказывается, что многие вопросы, которые возникают

при анализе живучести информационных сегментов, также непосред-

ственно относятся к теории перколяции.

Перед теорией перколяции стоят многие вопросы, которые вы-

ходят за стандартные рамки дискретной математики и теории вероят-

ностей [59].

Самая простая формулировка задачи теории перколяций сле-

дующая. Дана решетка из связей, случайная часть которых

—

«черная», проводящая, а остальная — «белая», не проводящая поток.

Необходимо найти такую минимальную концентрацию

«черных»

связей, при которой еще есть связный путь по «черным» связям сквозь

всю решетку, т.е. такую концентрацию, когда решетка в целом прово-

дит поток.

При



все связи решетки «белые» — решетка не проводит

поток. При увеличении концентрации «черных» — проводящих свя-

зей, при

p p



в решетке возникает перколяционный, проникающий

кластер из «черных» связей, соединяющий противоположные края

сетки. При размере сетки, стремящемся к бесконечности, размер этого

кластера также бесконечен, в связи с чем и был введен термин «бес-

конечный кластер». Другие совокупности соединенных между собой

связей конечного размера называются конечными кластерами.

При переходе через порог протекания, т.е. при возникновении

бесконечного кластера, свойства системы, характеризующие ее в це-

лом, резко изменяются. Если, например, «черная» связь проводит ток,

а «белая» нет, то проводимость всей системы

~ 1/

R G

вблизи

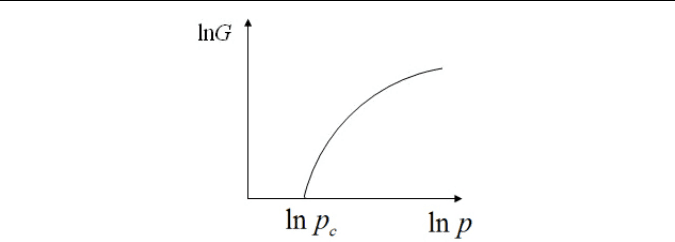
резко уменьшается. Учитывая логарифмический масштаб на рис. 15,

ясно, что вблизи порога протекания пропускная способность сети при

очень небольшом уменьшении

может резко упасть.

4. Критический уровень живучести систем

108

Рис. 15. Проводимость системы вблизи порога протекания

(в логарифмическом масштабе)

Казалось бы простая задача определения

, а «не поддалась»

точным методам теории вероятностей. За редкими исключениями

не удается вычислить аналитически — необходимо численное моде-

лирование.

В настоящее время известно много важных обобщений перко-

ляционной задачи, например, рассматриваются случаи, когда «непро-

водящие» связи проводят, но намного хуже проводящих; можно гово-

рить о значениях проводимости для разных связей; можно рассматри-

вать однонаправленные «диодные связи» и т.п.

К задачам, решаемым в рамках теории перколяции и анализа

сложных сетей, относятся такие, как определение предельного уровня

проводимости (пропускной способности), изменения длины пути и его

траектории (извилистости, параллельности) при приближении к пре-

дельному уровню проводимости, количества узлов, которые необхо-

димо удалить, чтобы нарушить связанность сети.

4.3. Характеристики перколяционных сетей

Существуют важные характеристики ребер сетей, по которым

происходит, например, прохождение тока, жидкости, информации (в

интересующих нас случаях).

Приведем некоторые из них:

( )

P p



— вероятность того, что случайным образом выбранный

узел принадлежит бесконечному кластеру, соединяющему две проти-

4.3. Характеристики перколяционных сетей

109

воположные стороны сети — эта характеристика имеет смысл выше по-

рога протекания, когда существует бесконечный кластер;

( )

s n p

S p

sn p

 



средний размер кластера (англ. — mean

cluster size), где

— число кластеров из

узлов, приходящихся на

один узел решетки — эта характеристика имеет смысл ниже порога

протекания, когда все существующие в системе кластеры имеют ко-

нечный размер;

( )



— корреляционная длина, характеризующая скорость

спада корреляций в решетке. Чтобы ввести ее, необходимо определить

парную корреляционную функцию

( , )

G r p p



(| |, )

i j

G r r p

 

( , )

i j

g r r



, где функция

( , )

i j

g r r

от радиусов векторов узлов

равна единице, если узлы связаны «черными» связями, принадлежа-

щими одному конечному кластеру, и равной нулю во всех остальных

случаях, а угловые скобки означают усреднение по всем узлам. При

 

корреляционная функция

( , )

G r p

убывает экспоненциально,

характерным масштабом при этом как раз и является корреляционная

длина

( , ) : exp[ / ( )]

G r p r p





Отметим, что при

p p



корреляционная длина

( )



расхо-

дится — это полностью соответствует качественным представлениям.

Чем ближе к порогу протекания

( )

p p



, тем меньше «черных» про-

водящих связей, тем существеннее каждая часть кластера, соединяю-

щая две «бесконечности», обрыв одной из них может сказаться далеко

от нее. На самом пороге протекания одна оборванная связь может раз-

рушить весь проводящий путь, называемый бесконечным кластером.

Структура бесконечного кластера не простая, на самом пороге проте-

кания он является фрактальным объектом, состоящим из связей, вхо-

дящих в этот кластер, с размерностью

( 2) / 1,896

d d d

 

    ,

( 3) 2,54.

d d

 

Вводят также и другие характеристики бесконечного кластера

— остов кластера (англ. backbone) — та часть кластера, по которой

4. Критический уровень живучести систем

110

происходит перенос, а также отсеченные «мертвые концы» (англ. dead

ends), и многие другие.

В более развитой и реалистичной теории протекания и «белые»

связи считаются проводящими, с проводимостью намного меньшей

«черных» (принято говорить, что в

раз меньше, где

0 1





При введении параметра

теория протекания может быть сформули-

рована в терминах теории фазовых переходов II рода, одном из самых

сложных разделов теоретической физики.

Описание проводимости перколяционной сети также может

быть сформулировано в терминах теории фазовых переходов II рода.

Для определенности будем говорить о так называемой эффективной

проводимости



, которая характеризует проводимость системы в це-

лом. Роль параметра порядка в этом случае играет



, а близость к

критической точке

( ) /

c c

p p p



  , где

— порог протекания. Со-

ответствующее скейлинговое соотношение для эффективной прово-

димости



имеет вид

( / ),

h f h

 

 



, ,

( ) ~ const, 0,

| | , .

z z

f z z

z z







 









 





В этих формулах

— так называемые критические индексы про-

водимости,

t q



 

Необходимо уточнить, что универсальное скейлинговое поведе-

ние



имеет место только вблизи порога протекания, т.е. при

| | 1





4.4. Перколяция на случайных сетях

Перколяцию можно рассматривать и на случайных сетях Эрдо-

ша–Реньи, Уаттса–Строгатса, и т.п. В этом случае вместо бесконечно-

го перколяционного кластера говорят о гигантской связной компонен-

те (англ. — giant connected component).