Дипломный проект - Проект мостового перехода через реку Селенга
Подождите немного. Документ загружается.

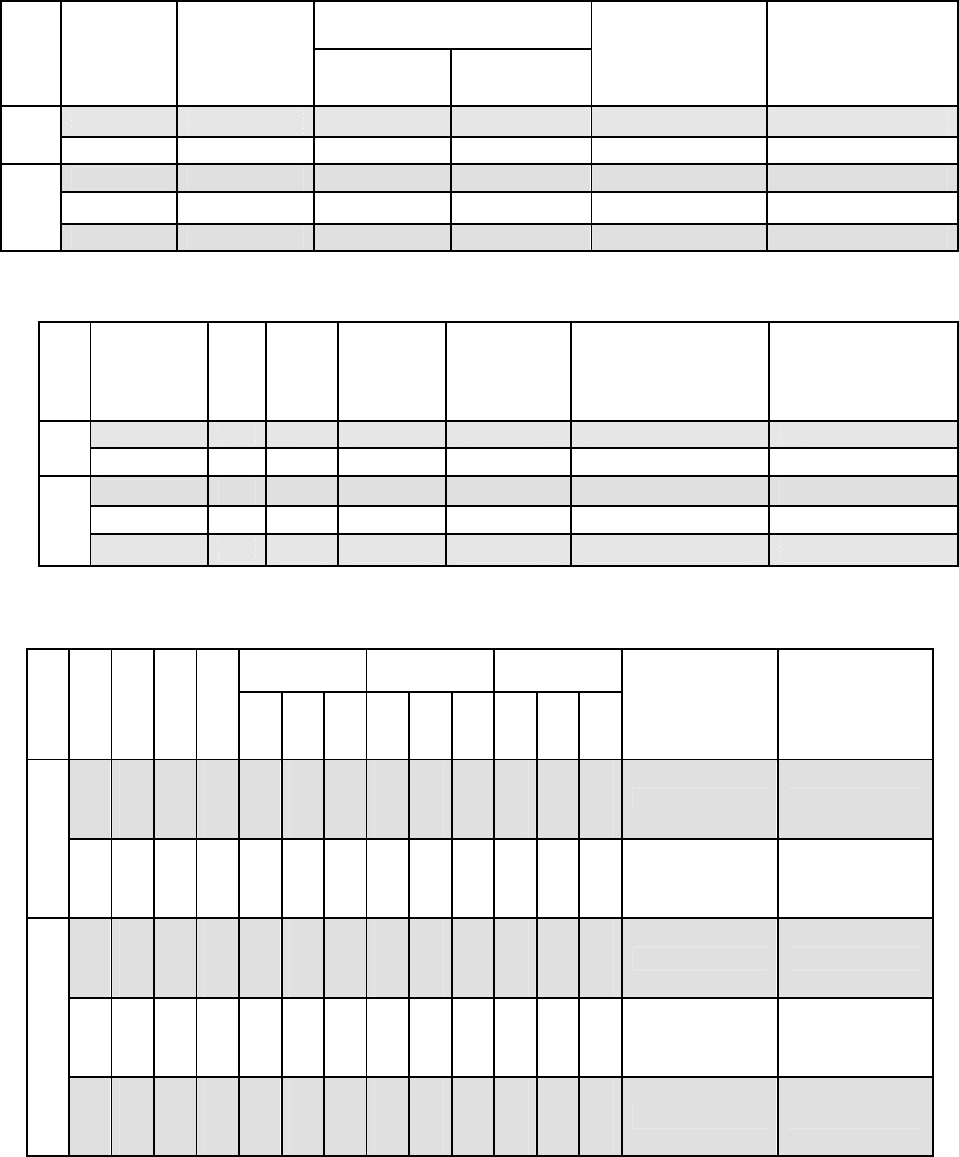
Все промежуточные расчёты сведены в таблицы 2,3,4 и в сводные таблицы 5,6.
Усилия от постоянной нагрузки.
Таблица 2.
Усилия от временной нагрузки НК 80
Таблица 3.
Сечен
Силовые
факторы
η γ
ƒ
(1+µ) ∑y
i
Нормативные
усилия, кНм
(кН)
Расчётные
усилия,
кНм (кН)
M
l/2
1 1 1,05 84,2 16503,2 17328,36
I
Q
l/2
1 1 1,07 1,94 380,24 406,86
M
оп
1 1 1,05 41,71 -8175,16 -8583,92
Q
оп
1 1 1,05 3,94 772,24 810,85
II
R
1 1 1,05 3,96 776,16 814,97
Усилия от временной нагрузки А11+толпа
Таблица 4.
А11 +
тележка
А11 + ν
Толпа
Сечени
Сил.
ф
акто
р
λ, м
ω
max,
м
2
∑y
i
η
γ
ƒ
(1+µ)
η
γ
ƒ
(1+µ)
η
γ
ƒ
(1+µ)
Нормативные
усилия,
S
n
, кНм (кН)
Расчётные
усилия,
S
r
, кНм (кН)
M
l/2
248,4
1246,
45
42,44
2
1,2
1,05
1,6
1,2
1,05
2
1,2
1,05
38034,8 47484,13
I
Q
l/2
186,3
22,74
1,49
2
1,2
1,07
1,6
1,2
1,07
2
1,2
1,96
848,50 1078,24
M
оп
248,4
1636,
2
21,01
2
1,2
1,05
1,6
1,2
1,05
2
1,2
1,96
-42432,6 -52887,77
Q
оп
248,4
70,88
1,99
2
1,2
1,05
1,6
1,2
1,05
2
1,2
1,96
2071,42 2584,98
II
R
248,4
141,7
7
1,99
2
1,2
1,05
1,6
1,2
1,05
2
1,2
1,96
3713,23 4628,66
Постоянная нагрузка,
кН/м
Сечения
Силовые
факторы
ω
с
q
n
q
γƒ
Нормативные
усилия,
S
n
, кНм (кН)
Расчётные
усилия,
S
r
, кНм (кН)
M
l/2
564,69 122,67 135,73 69270,52 76645,37
I
Q
l/2
4,391 122,67 135,73 538,64 595,99
M
оп
-1090,81 122,67 135,73 -133809,66 -148055,64
Q
оп
57,71 122,67 135,73 7079,29 7832,98
II
R
115,42 122,67 135,73 14158,57 15665,96
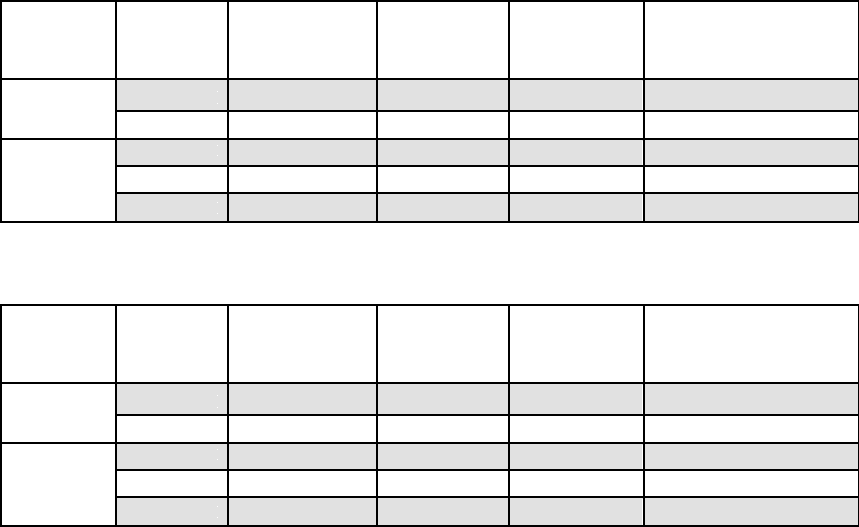
Сводная таблица нормативных усилий в балке от постоянных нагрузок.
Таблица 5.
Сечения
Силовые
факторы
Постоянная
нагрузка,
Sn, кН/м
НК-80,
S
НК ,
кН/м
А11+толпа
S
А11 ,
кН/м
Sn+ S
НК;
Sn+ S
А11;
кНм (кН)
M
l/2
89926,88 16503,2 38034,8 127961,68
I
Q
l/2
699,27 380,24 848,50 1547,77
M
оп
-173711,49 -8175,16 -42432,6 -216144,1
Q
оп
9190,32 772,24 2071,42 11261,74
II
R
18380,64 776,16 3713,23 22093,87
Сводная таблица расчётных усилий в балке от постоянных нагрузок.
Таблица 6.
Сечения
Силовые
факторы
Постоянная
нагрузка,
Sn, кН/м
НК-80,
S
НК ,
кН/м
А11+толпа
S
А11 ,
кН/м
Sn+ S
НК;
Sn+ S
А11;
кНм (кН)
M
l/2
17328,36 96720,10 47484,13 144204,23
I
Q
l/2
406,86 752,09 1078,24 1830,33
M
оп
-8583,92 -186833,94 -52887,77 -239721,71
Q
оп
810,85 9884,57 2584,98 12469,55
II
R
814,97 19769,14 4628,66 24397,8

15.1.2. Определение эффективной ширены главной балки.
Эффективная ширена пояса
efi
b
согласно ф. 145 СниПа:
iiefi
bb ⋅Σ=
ν
,
где ν
I
– коэффициент приведёния неравно распределенных напряжений на ширине участков пояса
i
b и
угловым равномерно распределённым напряжениям по всей эффективной ширине пояса
ef
b ; принимаемый
по таблице 7 Гибшмана;
i
b - ширина участка пояса, заключённая в рассматриваемом сечении между двумя точками с
максимальными напряжениями. При этом должны выполняться условия, оговоренные в формуле 145, стр.
79 СниПа:
)(04,0
)(02,0
бlb
аlb
p
pk
⋅≥
⋅
≥
bк = 3,0м
bк = 3,0м
b2 = 4,25м b2 = 4,25м
рис. К определению эффективной ширены главной балки.
Проверка условия для консоли:
мb
k
0,3
=
и l
p
= 126,0м , подставляя данные в условие (а) получим:
52,20,12602,00,3 =⋅≥
Следовательно, условие
pk
lb
⋅
≥ 02,0
- выполняется. Согласно Гибшман,
ν
К
= 0,98; отношение
024,0
0,126
0,3
==
p
k
l
b
; м
l
X
p
0,63
2
== .
Аналогично выполнялась проверка условия для коробки (
21
,bb ): мbb 25,4
21
=
=
, l
p
= 126,0м Подставляя
в условие (б) получим:
м04,50,12604,025,4
=
⋅
≥ . Условие
p
lb
⋅
≥ 04,0 - не выполняется, значит,
согласно СНиП
ν
2
=
ν
3
= 1,0.
Зная ширину поясов балки определим эффективную ширину балки:
мbb
мbbbbё
H
ef
ef
k
kiefi
В
5,80,125,422
38,140,125,4298,00,3222
3,23,2
3,23,2
=⋅⋅=⋅⋅=
=⋅⋅+⋅⋅=⋅⋅+⋅⋅=⋅Σ=
ν
ννν
Примечание: При определении коэффициента
ν
по таблице 7 подсчитывался коэффициент ортотропности ψ:
,97,0
012,03,0
014,025,0
=
⋅
⋅
=
⋅
⋅
=
⋅
=
ta
th
tа
A
прпрпр
ψ
где А
пр
- площадь продольного ребра, м
2
;
t = 0,012 м – толщина листа настила.
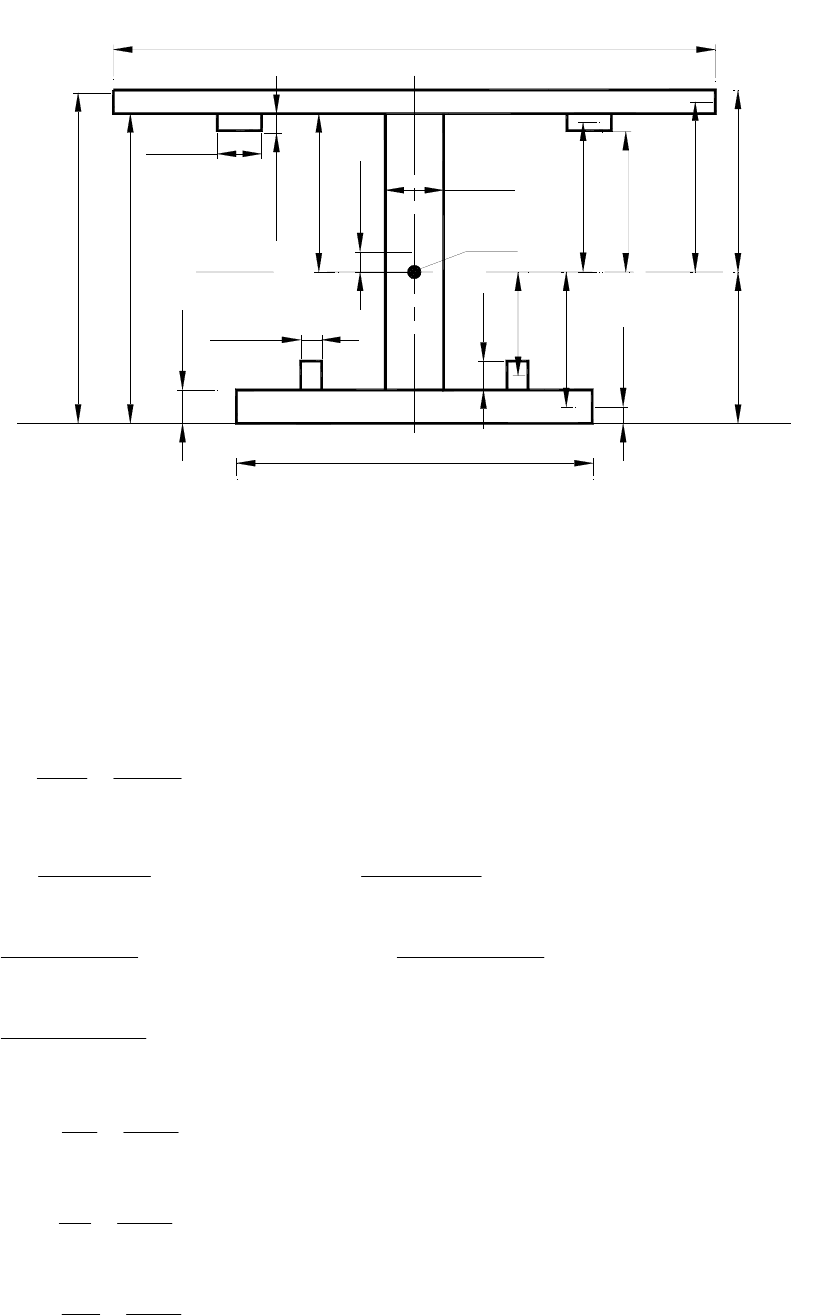
15.1.3. Определение геометрических характеристик поперечного сечения балки.
b = 14,38
b = 8,5
4
,
0
9
OO
4
,
1
0
0,198
0
,
0
2
0
,
0
2
5
0
,
3
2
,
0
3
2
,
1
9
0
,
1
7
Z
=
1
,
9
Z
=
2
,
2
1
,
8
9
2
1
,
7
6
5
0
,
1
6
5
1
,
8
8
8
ц.т.с
Z
'
=
1
,
6
4
0,024
0,34
Рисунок . Приведённое поперечное сечение (размеры даны в м.)
1. Площадь сечения:
2
0
7268,017256,016775,009768,0
1188,017,038,14012,023355,025,007,4024,03,0198,025,8012,0
м
A
=+++
+
=⋅
+
⋅
⋅
+
⋅
+
⋅⋅
+
⋅=
2. Статический момент инерции сечения относительно О-О:
3
5936,1)096,417256,0(
)965,308388,02()045,209768,0()17,00594,02()01,017,0(
м
S
OO
=⋅
+⋅
⋅
+
⋅
+
⋅
⋅+⋅=
−
3. Положение центра тяжести сечения:
м
A
S
X
O
OO
2,219,2
7268,0
5936,1
====
−
4. Момент инерции балки:
()
(
)
()
()
()
()
()
()
()
4
2
3
2
3
2
3
2
3
2
3
081,26203,02622,013749,024567,08153,0896,117256,0
12
012,038,14
765,1083875,0
12
25,03355,0
2165,009768,0
12
024,007,4
03,20594,0
12
3,0198,0
219,217,0
12
)02,0(5,8
м
I
=++++=
⋅+
⋅
+
⋅+
⋅
⋅+
⋅+
⋅
+
⋅+
⋅
⋅+
⋅+
⋅
=
5. Момент сопротивления нижнего сжатого горизонтального ребра:
3
946,0
20,2
081,2
м
Z
I
W
H
H
Z
===
6. Момент сопротивления нижнего сжатого горизонтального ребра:
3
095,1
90,1
081,2
м
Z
I
W
B
B
Z
===
7. Момент сопротивления нижней грани сжатого продольного ребра:
3
'
'
2687,1
64,1
081,2
м
Z
I
W
B
B
Z
===
8. Статический минимальный и максимальный моменты отсечённой части сечения:
3
493,003,20594,019,217,0 мS
MIN
=⋅+⋅= ;

3
51,001612,0493,0165,007,4024,0493,0 мSSS
т
cMINMAX
=+=⋅⋅+=+=
15.1.4. Расчёт главной балки по прочности по нормальным напряжениям.
Расчёт по прочности выполнялся в соответствии с СНиП, стр. 78, ф. 142:
y
z
d
Rm
W
M
⋅≤
⋅
=
χ
σ
,
где M
d
= 144204,23 кH/м – расчётный изгибающий момент сечения;
W
Z
= 1,019 м
3
– момент сопротивления сечения;
m = 1 – коэффициент условия работы;
R
y
= 295 мПа – расчётное сопротивление стали 15ХСНД по текучести;
R
S
= 0,58R
y
= 171,10 мПа.
Согласно СНиП, стр. 78 при определении коэффициента пластических
деформаций, необходимо проверить условие, предварительно определив
среднее касательное напряжение в стенке балки:
2
2/
/0,18738
024,007,4
33,1830
мкН
th
Q
ww
l
d
m
=
⋅
=
⋅
=
τ
где Q
d
= 1830,33 кН – расчётная перерезывающая сила в середине пролёта;
h
w
= 4,07 м – высота балки (без ортотропной плиты настила);
t
w
= 0,024 м – суммарная толщина стенок балки;
Условие
Sm
R25,0≤
τ
- выполняется и коэффициент χ = χ
1
, при этом должно выполняться условие:
1
0
χ
χ
≤≤ . Коэффициент χ
1
= 1,019 согласно СНиП, таблице 61 (определялся по интерполяции в
зависимости от
222
4402,0;17,0;0977,0 мAмAмA
fMINW
=== ). Условие
1
0
χ
χ
≤≤ - выполняется.
Напряжение в верхнем горизонтальном листе:
;20,129
0951,1019,1
1023,144204
3
3
мПа
м
Нм
B
=
⋅
⋅
=
σ
;29520,129 мПамПа
<
Напряжение в нижнем горизонтальном листе:
;60,149
946,0019,1
1023,144204
3
3
мПа
м
Нм
Н
=
⋅
⋅
=
σ
;29560,149 мПамПа
<
Напряжение в нижней грани продольного ребра:
;54,111
2687,1019,1
1023,144204
3
3
'
мПа
м
Нм
B
=
⋅
⋅
=
σ
.29554,111 мПамПа
<
Все найденные напряжения удовлетворяют условию
yi
mR
≤
σ
.
15.1.5 Расчёт главной балки по прочности по касательным напряжениям.
Согласно п. 4.30 СниПа, значение касательных напряжений в сечениях стенки изгибаемых элементов при
0===
YX
MMM должны удовлетворять условию:
mR
tI
SQ
S
W
MAXd
⋅≤
⋅⋅
⋅
=
2
χ
τ
,
значения R
S
, S
MAX
, I, t
W
описаны и определены в п.??????.
χ
2
– коэффициент, определяемый по формуле 160 СниПа:
;07,18
024,008095,2
493,033,1830
,
мПа
tI
SQ
W
MINd
efMIN
=
⋅
⋅
=
⋅
⋅
=
τ

мПа
tI
SQ
W
MAXd
efMAX
7,18
024,008095,2
51,033,1830
,
=
⋅
⋅
=
⋅
⋅
=
τ
;
0084,1
70,18
07,18
25,025,125,025,1
,
,
2
=⋅−=⋅−=
мПа
мПа
efMAX
efMIN
τ
τ
χ
Касательное напряжение в середине пролёта на уровне нейтральной оси:
мПа
м
кНм
мм
мкН
54,18
05036,0
468,933
024,008095,20084,1
51,033,1830
3
3
4
3
==
⋅⋅
⋅
=
τ
15.1.6. Расчёт главной балки по прочности по приведённым напряжениям.
P/2 = 98
a = 0,2
a' = 0,344
t
т. А
P/2
ц.т.с.
т. А
h
=
0
,
0
6
t
=
0
,
0
1
2
Z
'
'
=
1
,
8
8
8
Рисунок . Схема расчёта главной балки по прочности (размеры даны в
м.)
Согласно СНиП , п. 4.31, стр. 80, формула 161 для стенок балок должно
выполняться условие:
mR
Y
XY
YYXX
'222
3)()(
γτσσσσ
≤++−
, при этом mR
Sm
≤
τ
,
где
−
X
σ
нормальное (положительное при сжатии) напряжение в проверяемой точке сечения (т. А)
срединной плоскости стенки, параллейное оси балки;
−
Y
σ
напряжение, перпендикулярное оси балки и определяемое по приложению 16 СниПа;
15,1
'
=
γ
при
0=
Y
σ
и 10,1
'
=
γ
при
0
≠
Y
σ
;
−== мПа
mXY
73,18
τ
τ
среднее касательное напряжение в стенке балки;
−= мПаR
Y
295 расчётное сопротивление стали марки 15ХСНД;
Нормальное напряжение в т. А (в пролёте) определялось по следующей формуле:
мПа
м
мкН
W
M
BZ
l
d
X
42,128
102,1019,1
/23,144204
3
''
2/
=
⋅
=
⋅
=
χ
σ
где
3
4
''
102,1
888,1
08095,2
''
м
м
м
Z
I
W
B
BZ
=== - момент сопротивления сечения;
−= мкНM
d
/23,144204 расчётный момент в пролёте;
−= 019,1
χ
коэффициент пластических деформаций в пролёте.

Напряжения, возникающие от местного воздействия колеса нагрузки НК80 (ввиду
большей величины по сравнению с А11) по формуле:
мПа
мм
кН
a
P
Y
47,33
244,0012,0
2/196
'
2/
=
⋅
=
⋅
=
δ
σ
; mR
YY
<
σ
−
=<= мПаRмПа
YY
0,29547,33
σ
условие выполняется.
где
−= м012,0
δ
толщина стенки балки;
() ( )
−
=
+
⋅+=+⋅+= мhtaa 244,001,0012,022,02' площадь распределения давления на стенку
балки;
a = 0,2 – площадь касания колеса нагрузки НК80;
t = 0,012 м – толщина листа настила;
h = 0,01 м – толщина слоёв дорожной одежды проезжей части.
Проверка условия по п. 4.31:
()
0,12951,173,183)47,33(47,3342,128)42,128(
2
22
⋅⋅≤++⋅− мПа
мПамПа 0,32468,12125 ≤
−≤ мПамПа 0,32412,110 условие прочности выполнено.
Прочность главной балки по приведённым напряжениям обеспечена.
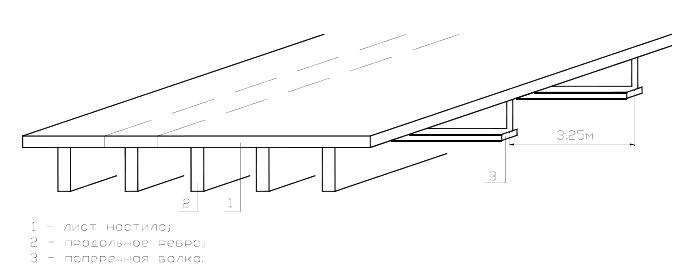
15.2. Расчёт ортотропной плиты проезжей части.
Рисунок . Схема к расчёту ортотропной плиты проезжей части.
Расчёт ортотропной плиты проводился по программе PORT.
Параметры конструкции:
Число полос автомобильной нагрузки N = 2
Расстояние между стенками главных балок L= 8.5 м
Расстояние между поперечными балками l = 3.25 м
Шаг продольных ребер а =0.3 м
Толщина покрытия проезжей части б = 6 см
Расчетная нагрузка от веса покрытия q = 1.38 кН/м^2
Расчетное сопротивление стали Ry = 295 МПа
Характеристики поперечной балки:
Высота стенки h = 800 мм
Толщина стенки б = 16 мм
Ширина нижней полки b = 300 мм
Толщина нижней полки б = 18 мм
Характеристики продольного ребра:
Высота ребра h = 250 мм
Толщина ребра б = 14 мм
*** ЛИСТ НАСТИЛА ***
Минимальная толщина листа настила из условия
совместной работы с покрытием
t(min) = 6.997005 мм
Минимальная толщина листа по условию прочности:
-для листа как неразрезной балки на жестких опорах (по М(оп))
t(h) = 9.857305 мм
(при изгибающем моменте М=-1.528752 кНм от собст. веса и А11)
-для листа как неразрезной балки на упругих опорах (по М(оп))
t(h) = 9.314474 мм
(при характеристике жесткости листа ALFA= 27.48605
и изгибающем моменте М=-1.365015 кНм от собст. веса и А11)
Минимальная толщина листа по условиям
технологии изготовления
t(тех)=12 мм
--------------------------------------------------------------
Окончательно получаем требуемую толщину листа t= 12 мм
ХАРАКТЕРИСТИКИ
ЛИСТА
жесткие
опоры
упругие опоры
( ALFA= 27.48605 )
Толщина проката (мм): 9.857305 9.314474
Площадь поперечного
сечения (м^2): 3.154338E-03 2.980632E-03
Момент инерции (м^4): 2.554132E-08 2.154983E-08
Изгибающие моменты (кН*м):
-опорное сечение: от НК -1.073539 -1.054168
от А11 -1.523972 -1.360576
от собств.веса -4.779896E-03 -4.439198E-03
-в середине пролета: от НК 0.4418545 0.5361981
от А11 0.6468084 0.9417503
от собств.веса 2.740962E-03 2.665186E-03
Толщина проката, принятая
при подсчете собств. веса
и параметра ALFA, (мм): 6.997005 6.997005
Окончательно принята толщина листа t= 12 мм
*** ПРОДОЛЬНОЕ РЕБРО ***
ПРОДОЛЬНОЕ РЕБРО
( лист настила t= 12 мм, высота h= 250 мм, толщина б= 14 мм )
ХАРАКТЕРИСТИКИ
РЕБРА
жесткие
опоры
упругие опоры
( ALFA =
36.64754)
Площадь попер.сечения(м^2): 7.100001E-03 7.100001E-03
Момент инерции(м^4): 4.872711E-05 4.872711E-05
Моменты сопротивления(м^3):
-для верхнего волокна 6.904061E-04 6.904061E-04
-для нижнего волокна 2.545526E-04 2.545526E-04
Изгибающие моменты(кН*м)
-опорное сечение: от НК -30.97778 -18.98626
от А11 -24.02582 -10.99934
от собств.веса -0.9023349 -0.8382526
-в середине пролета: от НК 23.61797 26.00824
от А11 29.2897 29.87086
от собств.веса 0.517431 0.5035439
Нормальные напряжения (МПа):
опорное сечение
-верхнее волокно 46.1759 28.71428
-нижнее волокно -125.2398 -77.87984
в середине пролета
-верхнее волокно -43.17334 -43.99498
-нижнее волокно 117.0962 119.3247
*** ПОПЕРЕЧНАЯ БАЛКА ***
( пролет L = 8.5 м, эффективная ширина пояса l(f) = 2.561 м )
ХАРАКТЕРИСТИКИ
БАЛКИ
р
азрезная
балка
защемлённая
балка
Площадь попер.сечения(м^2): 0.048932 0.048932
ЛИСТ НАСТИЛА
ПОПЕРЕЧНАЯ БАЛКА
Момент инерции(м^4): 4.49733E-03 4.49733E-03
Моменты сопротивления(м^3):
-для верхнего волокна 2.224797E-02 2.224797E-02
-для нижнего волокна 7.163015E-03 7.163015E-03
Изгибающие моменты(кН*м)
-опорное сечение: от НК 0 -621.5789
от А11 0 -700.3585
от собств.веса 0 -75.50957
-в середине пролета: от НК 851.0989 351.1633
от А11 1053.064 393.3383
от собств.веса 113.2644 37.75478
Нормальные напряжения (МПа):
опорное сечение
-верхнее волокно 0 34.87366
-нижнее волокно 0 -108.3159
в середине пролета
-верхнее волокно -52.42405 -19.37674
-нижнее волокно 162.8265 60.18319
ПРОГИБЫ В СЕРЕДИНЕ ПРОЛЕТА ПОПЕРЕЧНОЙ БАЛКИ (ММ)
СХЕМА
НК-80
НАГРУЗКА
А11
разрезная 6.190869 8.161467
балка
защемленная 1.317381 1.730305
балка
--------------------------------------------------------------
При допускаемом прогибе [f] = L/400 = 21.25
15.2.1. Проверка прочности поперечной балки.
Ri Ri
т. С
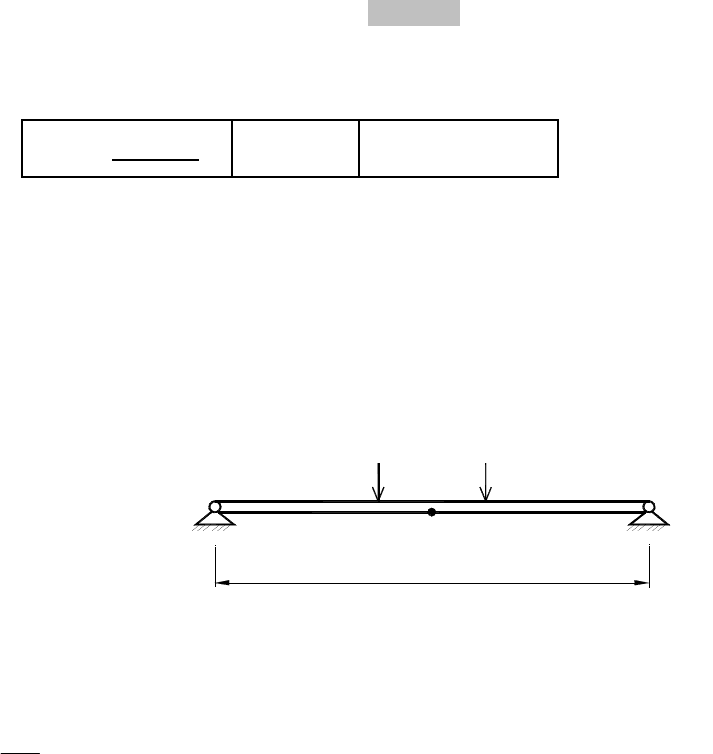
126,00 м
Рисунок . Схема к проверке прочности нижнего волокна балки.
Проверка прочности крайнего нижнего волокна поперечной балки
проводилась в сечении в середине пролёта (т.С) и согласно СНиП прил. 18,
п.8, формула 8:
mR
Y
YP
≤
χ
σ
,
где m = 1 – коэффициент условия работы, принятый по таблице 60 / /;
χ
= 1,019 – коэффициент принятый по таблице 61 / / при расчёте балки по нормальным
напряжениям (в сечении в середине пролёта);
−= мПа
YP
80,162
σ
напряжение в нижнем волокне поперечной балки в сечении в середине пролёта и
определённый по программе PORT;
R
Y
= 295 мПа – расчётное сопротивление стали марки 15 ХСНД.
Проверка условия:
