Дибров М.В. Маршрутизаторы

Подождите немного. Документ загружается.

Пример 15.3 – Информация, выводимая командой show ip ospf database

router

rl# show ip ospf database router 3.3.3.3

OSPF Router with ID (1.1.1.1) (Process ID 2)

Router Link States (Area 0)

Routing Bit Set on this LSA

LS age: 5 (DoNotAge)

Options: (No TOS–capability, DC)

LS Type: Router Links

Link State ID: 3.3.3.3

Advertising Router: 3.3.3.3

LS Seq Number: 80000002

Checksum: 0x3990

Length: 36

Area Border Router

Number of Links: 1

Link connected to: a Virtual Link

(Link ID) Neighboring Router ID: 1.1.1.1

(Link Data) Router Interface address: 6.0.0.3

Number of TOS metrics: 0

TOS 0 Metrics: 65

Пример 15.4 – Информация, выводимая командой debug ip ospf adj

r3# debug ip ospf adj

lw2d: OSPF: Rev hello from 1.1.1.1 area 0 from 0SPF_VL3 5.0.0.1

lw2d: OSPF: 2 Way Communication to 1.1.1.1 on OSPF_VL3, state 2WAY

lw2d: OSPF: Send DBD to 1.1.1.1 on OSPF_VL3 seq 0xD1C opt 0x62 flag 0x7 len 32

lw2d: OSPF: End of hello processing

lw2d: OSPF: Rev DBD from 1.1.1.1 on OSPF_VL3 seq 0x1617 opt 0x22 flag 0x7 len

32 mtu 0 state EXSTART

lw2d: OSPF: First DBD and we are not SLAVE

lw2d: OSPF: Rev DBD from 1.1.1.1 on OSPF_VL3 seq OxDIC opt 0x22 flag 0x2 len

17 2 mtu 0 state EXSTART

lw2d: OSPF: NBR Negotiation Done. We are the MASTER

lw2d: OSPF: Send DBD to 1.1.1.1 on OSPF_VL3 seq 0xD1D opt 0x62 flag 0x3 len

172

lw2d: OSPF: Database request to 1.1.1.1

lw2d: OSPF: sent LS REQ packet to 5.0.0.1, length 36

lw2d: OSPF: Rev DBD from 1.1.1.1 on OSPF_VL3 seq 0xD1D opt 0x22 flag 0x0 len

32 mtu 0 state EXCHANGE

lw2d: OSPF: Send DBD to 1.1.1.1 on OSPF_VL3 seq 0xD1E opt 0x62 flag 0x1 len 32

lw2d: OSPF: Rev DBD from 1.1.1.1 on OSPF_VL3 seq 0xD1E opt 0x22 flag 0x0 len

32 mtu 0 state EXCHANGE

lw2d: OSPF: Exchange Done with 1.1.1.1 on OSPF_VL3

lw2d: OSPF: Synchronized with 1.1.1.1 on 0SPF_VL3, state FULL

lw2d: OSPF: Build router LSA for area 0, router ID 3.3.3.3, seq 0x80000029

lw2d: OSPF: Dead event ignored for 1.1.1.1 on demand circuit OSPF_VL3

261

16 Перераспределение маршрутной информации

16.1 Понятие перераспределения маршрутной информации

В некоторых ситуациях бывает необходимо использовать несколько

протоколов маршрутизации на одном маршрутизаторе. Наиболее распростра-

ненными причинами являются:

– Происходит объединение двух сетей передачи данных, а маршрутиза-

ция в них обеспечивается с помощью различных протоколов маршрутизации.

Если одна из сетей передачи данных перед объединением полностью не пере-

водится на протокол маршрутизации, используемый в другой сети, то в дан-

ной ситуации, по крайней мере, на граничных маршрутизаторах объединяе-

мых сетей передачи данных должны быть запущены оба протокола маршру-

тизации. Для обеспечения связи между данными сетями, пограничные марш-

рутизаторы должны проводить преобразование маршрутной информации

между двумя протоколами маршрутизации.

– Сеть передачи данных переводится с одного протокола маршрутиза-

ции на другой. Если миграция не производиться на всех маршрутизаторах од-

новременно, то на некоторых ключевых маршрутизаторах оба протокола

маршрутизации должны сосуществовать определенное время, которое потре-

буется для полного перехода на новый протокол маршрутизации. В этом слу-

чае, чтобы обеспечить связь между частью сети, которая уже была переведена

на новый протокол маршрутизации, и частью, где это еще не сделано, ключе-

вые маршрутизаторы должны не только позволять сосуществовать обоим

протоколам маршрутизации, но также и выполнять преобразование маршрут-

ной информации между этими протоколами маршрутизации.

– В сети передачи данных могут существовать сервера или рабочие

станции, которым необходимо участвовать в процессе динамической маршру-

тизации, без объявления собственной маршрутной информации. Примером

подобной ситуации могут выступать сервера под управлением ОС Unix или

Windows, которые используют протокол маршрутизации RIP, а сеть передачи

данных реализована на маршрутизаторах Cisco, на которых запущен протокол

маршрутизации EIGRP. В такой ситуации маршрутизаторы, которые подклю-

чены к сегментам сети, в которых имеются интеллектуальные хосты, должны

конвертировать маршрутную информацию протокола EIGRP в протокол RIP.

Существует значительно больше случаев, требующих работы несколь-

ких протоколов маршрутизации на одном маршрутизаторе. Не вдаваясь в по-

дробности каждой из таких ситуаций, очевидно, что все они налагают одно

требование: помимо простого сосуществования, протоколы маршрутизации

должны обмениваться маршрутной информацией.

262

Простого исполнения нескольких протоколов маршрутизации на одном

и том же маршрутизаторе недостаточно для обмена маршрутной информаци-

ей между этими протоколами.

Маршрутизаторы автоматически не производят обмен маршрутной ин-

формации между протоколами маршрутизации запущенными на них. Причи-

на этого заключается в том, что несколько протоколов маршрутизации, даже

присутствуя на одном маршрутизаторе, могут выполнять различные задачи.

Следовательно, обмен маршрутной информацией между ними может быть не-

желателен.

Другой причиной того, что несколько протоколов маршрутизации запу-

щенные на одном маршрутизаторе не обмениваются маршрутной информаци-

ей автоматически, является то, что различные протоколы маршрутизации по-

разному рассчитывают метрики маршрутов, вследствие чего эти метрики не-

совместимы. Например, протоколом RIP в качестве метрики используется ко-

личество переходов до сети получателя, тогда как протокол EIGRP использу-

ет комбинированную метрику. Метрика является одним из важнейших пара-

метров маршрута рассматриваемых протоколом маршрутизации при построе-

нии таблицы маршрутизации. Поскольку метрики несовместимы, не суще-

ствует простого способа адекватно преобразовывать метрики маршрутов рас-

считанных различными протоколами маршрутизации. Неадекватное преоб-

разование может с большой вероятностью привести к возникновению марш-

рутных петель.

Процесс преобразования маршрутной информации между различными

ее источниками называется перераспределением маршрутной информации

(routing information redistribution) или просто перераспределением.

Источники маршрутной информации не ограничиваются динамически-

ми протоколами маршрутизации. Они также включают статические и присо-

единенные маршруты. Однако статические и присоединенные маршруты мо-

гут быть лишь источником маршрутной информации для перераспределения.

По очевидным причинам перераспределение не может производиться в стати-

ческие и присоединенные маршруты.

Включение перераспределения на маршрутизаторе обычно предполага-

ет указание трех следующих компонентов:

– Источника маршрутной информации, которая должна быть перерас-

пределена.

– Получателя маршрутной информации в виде протокола маршрутиза-

ции, в который перераспределяется маршрутная информация.

– Метрик, которые должны использоваться протоколом маршрутизации

при объявлении в домен маршрутизации динамического протокола перерас-

пределенной маршрутной информации.

Последний компонент сводиться, как правило, к указанию одной или

нескольких фиксированных метрик, которые должны использоваться прото-

колом маршрутизации при объявлении перераспределенной маршрутной ин-

263

формации. Если указана лишь одна метрика, протокол маршрутизации будет

использовать ее для всех перераспределяемых сетей получателей, а если ука-

зано несколько, протокол маршрутизации использует каждую из них для ин-

дивидуального подмножества перераспределяемых сетей получателей в соот-

ветствии с отдельно указанными правилами.

Перераспределение маршрутной информации необязательно должно

быть двухсторонним. Если информация одного протокола маршрутизации

перераспределяется в другой, информация последнего не обязательно должна

перераспределяться в первый. Возможно, а в некоторых случаях и желатель-

но перераспределение маршрутной информации только из одного протокола

в другой, но не наоборот.

В качестве примера можно рассмотреть такую ситуацию. В сети переда-

чи данных имеется область, в которой маршрутизация осуществляется при

помощи устаревшего сетевого оборудования, на котором не может быть раз-

вернут основной протокол маршрутизации применяемый в корпоративной

сети передачи данных. В данной ситуации маршрутная информация должна

быть перераспределена из данного сегмента в общий домен маршрутизации, а

обратное перераспределение может привести к перегрузке маршрутной ин-

формацией сетевого оборудования расположенного внутри данной области. В

данном случае обеспечение маршрутной информацией о внешних сетях полу-

чателях маршрутизаторов внутри области, может быть выполнено распро-

странением маршрута по умолчанию на граничный маршрутизатор области,

который обладает полной маршрутной информацией.

16.2 Понятие метрического домена

Различные протоколы маршрутизации используют различные алгорит-

мы расчета метрик. Независимо от конкретного алгоритма расчета метрики,

метрики всех протоколов маршрутизации обладают одним общим свойством

– они увеличиваются с увеличением количества переходов на пути от сети

получателя.

Формально накопительный характер метрики можно описать выраже-

нием (16.1).

∀ d и d` где d`>d, M(d`)>M(d)

(16.1)

где d и d` – количество переходов на пути от сети получателя,

M(x) – функция метрики.

Учитывая это общее свойство метрик протоколов маршрутизации,

определим метрический домен протокола маршрутизации как часть сети

передачи данных, в которой метрики протокола маршрутизации отражают

264

расстояние до сети получателя, и удовлетворяют выражению (16.1). Метрики

рассчитываются в соответствии с алгоритмом, предписанным запущенным на

маршрутизаторах протоколом маршрутизации. Другими словами, любой

маршрутизатор в пределах метрического домена протокола маршрутизации

рассчитывает метрики маршрутов до сетей получателей, находящихся в пре-

делах метрического домена, в соответствии с алгоритмом, предписанным

протоколом маршрутизации. Если маршрутизатор использует любой другой

алгоритм для расчета метрики маршрута до сети получателя, то этот маршру-

тизатор находится за пределами метрического домена, которому принадле-

жит сеть получатель.

172.16.14.0/28

172.16.14.16/28

172.16.14.32/28

172.16.14.64/28

192.168 .1.0/28

Домен 172.16.0.0 Домен 192.168.1.0

RIP v1

Рисунок 16.1 – Пример метрического домена

Примером метрического домена (Рисунок 16.1) протокола RIP v1 яв-

ляется непрерывная группа сегментов, подсети которых принадлежат одной и

той же классовой сети. Граница такого метрического домена для протокола

RIP пролегает по маршрутизатору R1, который, кроме того, имеет подключе-

ние к сегменту, принадлежащему другой классовой сети.

Как мы знаем, при формировании маршрутных обновлений протоколом

RIP, которые должны быть отправлены, через интерфейсы, принадлежащие

другой классовой сети, маршрутизатор производит автоматическое суммиро-

вание маршрутов до маршрута на классовую сеть, метрику которого устанав-

ливает равной 1, отбрасывая тем самым накопленную информацию о метри-

ках частных маршрутов. Очевидно, что любой маршрутизатор не принадле-

жащий классовой сети 172.16.0.0, может получать только суммарный марш-

рут на классовую сеть, а не частные маршруты до сетей получателей. Такие

маршрутизаторы будут воспринимать любую сеть получатель в пределах дан-

ного метрического домена с одной метрикой – той, которая имеется у них для

данной классовой сети. Маршрутизаторы принадлежащие другой классовой

сети больше не вычисляют метрики маршрутов, до сетей получателей в пре-

делах данного метрического домена в соответствии с алгоритмом протокола

265

RIP, а значит, такие маршрутизаторы находятся за пределами метрического

домена 172.16.0.0.

Приведенный выше пример представляет собой естественную границу

метрического домена, обусловленную суммированием маршрутов до сетей

получателей на границе классовой сети.

Граница метрического домена также создается на маршрутизаторах вы-

полняющих, перераспределение маршрутной информации, которое заменяет

накопленные метрики одной или несколькими фиксированными метриками.

В зависимости от протокола маршрутизации, перераспределение может, со-

провождаться или не сопровождаться суммированием маршрутов. Если оно

сопровождаются суммированием, полученная граница метрического домена

не отличается от естественной границы. В обратном случае граница носит

полностью искусственный характер – частные маршруты пересекают границу

не измененным, но их метрики заменяются на фиксированную величину.

Искусственные границы метрических доменов могут негативно влиять

на работу сети передачи данных, создавая маршрутные петли.

16.3 Маршрутные петли

Маршрутные петли (routing loops) представляют собой маршруты в сети

передачи данных, которые приводят на один и тот же маршрутизатор более

одного раза. Маршрутные петли крайне не желательны, поскольку трафику

приходится преодолевать дополнительный путь лишь для того, чтобы при-

быть на тот же самый маршрутизатор. Это в свою очередь приводит к задерж-

ке трафика, или даже к полной невозможности его доставки сетям получате-

лям. Маршрутные петли подвергают сеть передачи данных избыточной на-

грузке и приводят к огромному количеству операций по обработке поступаю-

щего трафика на причастных маршрутизаторах.

Маршрутные петли могут быть классифицированы как:

Короткоживущие маршрутные петли – петли существующие непродол-

жительное время, обычно не более пары минут.

Долгоживущие маршрутные петли – петли существующие продолжи-

тельное время, от нескольких минут до бесконечности.

Возникновение короткоживущих маршрутных петель обусловлено про-

цессами, происходящими во время схождения сети, после произошедших в

ней изменений. Время возможного существования таких маршрутных петель

зависит от скорости схождения сети и от протокола маршрутизации применя-

емого в сети передачи данных. Короткоживущие маршрутные петли имеют

возможность самоустраняться за определенный, не продолжительный период

времени.

Возникновение долгоживущих маршрутных петель обусловлено ошиб-

ками в настройке процесса маршрутизации внутри домена маршрутизации.

266

Обычно долгоживущие маршрутные петли не исчезают, если не принять мер

к устранению тех ошибок в процессе маршрутизации которые привели к их

возникновению. Долгоживущие маршрутные петли могут быть как постоян-

ными, так и периодическими. Постоянные маршрутные петли существую все

время, тогда как периодические проходят через циклы, исчезая и появляясь

вновь.

Протоколы маршрутизации разрабатываются самостабилизирующими-

ся. Тогда как временная нестабильность, вызываемая изменениями в тополо-

гии сети передачи данных и часто сопровождаемая короткоживущими марш-

рутными петлями, зачастую неизбежна. Протоколы маршрутизации преодо-

левают нестабильность и устанавливают маршрутизацию без петель. Ни один

протокол маршрутизации не спроектирован так, чтобы позволить долгоживу-

щим маршрутным петлям образоваться в какой-либо момент работы.

Все протоколы маршрутизации базируются на математических моде-

лях, для которых доказано, что они не вызывают появление долгоживущих

маршрутных петель. Большинство этих математических моделей обеспечива-

ют функционирование без образование петель, посредством соблюдения

условия, что метрики, связанные с местами назначения, растут с добавлением

каждого дополнительного перехода на пути к месту назначения.

Формально можно описать, что если маршрутизатор R1 выбирает

маршрут до сети получателя D через маршрутизатор R2, то M1>M2, где M1 и

M2 являются метриками маршрута до сети получателя D маршрутизаторов

R1 и R2 соответственно. Другими словами, чем дальше место назначения, тем

больше метрика. Если это допущение соблюдается, маршрутная петля образо-

ваться не может.

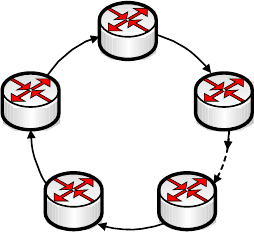
Доказывается это просто. Будем считать, что в сети передачи данных N

все маршрутизаторы выбирают маршруты к сетям получателям на основе вы-

шеупомянутого допущения. Предположим, однако, что петля существует и

имеется маршрутизатор R1, установивший маршрут к сети получателю D че-

рез маршрутизатор R2, который в свою очередь установил маршрут к D через

маршрутизатор R3, и так далее до маршрутизатора Rn, установившего марш-

рут к D через маршрутизатор R1. Такая ситуация показана на рисунке 16.2.

Как мы предположили, допущение соблюдается, следовательно, метри-

ки всех маршрутов должны соответствовать неравенству (16.2).

> M

… M

n-2

> M

n-1

(16.2)

Неравенство (16.2) сводится к M

> M

. Следовательно, наша исходная

предпосылка о том, что петля может существовать даже в том случае, если

все маршрутизаторы соблюдают принятое допущение, неверна.

267

R1 R3

Rn Rn-

Mn-

Mn-1Mn-

Рисунок 16.2 – Предположение об образовании маршрутной петли

Маршрутные петли не возникают в сети передачи данных, в которой

маршрутизация поддерживается средствами одного протокола маршрутиза-

ции, пока не нарушены ограничения протокола, такие как максимальное ко-

личество переходов, в маршруте к сети получателю, а сетевое оборудование и

его программное обеспечение работают в нормальном режиме.

В случае если маршрутизация в сети передачи данных поддерживается

с помощью более чем одного протокола маршрутизации или комбинации ста-

тической и динамической маршрутизации, возникает возможность возникно-

вения маршрутных петель. Эта возможность увеличивается при перераспре-

делении маршрутной информации между протоколами маршрутизации. По-

скольку в процессе перераспределения объединяются домены отдельных про-

токолов маршрутизации, тогда как метрические домены остаются отдельны-

ми. Сети получатели, находящиеся в пределах одного домена протокола

маршрутизации, становятся доступными из домена другого протокола марш-

рутизации с одной и той же метрикой.

16.3.1 Односторонние перераспределение маршрутной информации

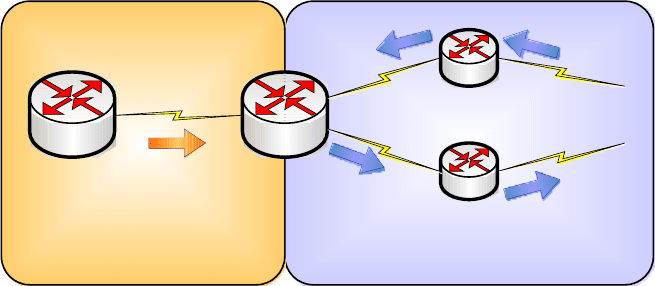
На рисунке 16.3 показана сеть передачи данных, в которой потенциаль-

ным источником маршрутных петель может быть одна точка одностороннего

перераспределения маршрутной информации.

Маршрутизатор R1 объявляет сети получатели, имеющиеся в части сети

передачи данный N1 с использованием протокола маршрутизации RP1 марш-

рутизатору R2, который затем перераспределяет эти сети получатели в прото-

кол маршрутизации RP2. Маршрутизатор R2 объявляет перераспределенные

сети получатели своим соседям, находящимся в части сети передачи данных

N2. Административное расстояние протокола маршрутизации RP1 равно A1,

а административное расстояние протокола маршрутизации RP2 равно A2.

Административные расстояния таковы, что A2<A1.

268

R1 R2

M = M 1

Сеть N1,

Протокол маршрутизации RP1,

Административное расстояние RP1 = A1

A1>A2

Сеть N2,

Протокол маршрутизации RP2,

Административное расстояние RP2 = A2

A2<A1

Рисунок 16.3 – Образование маршрутной петли при одностороннем

перераспределении маршрутной информации

Стрелки внутри N2 показывают поток маршрутных обновлений, кото-

рый, если имеет место, приводит к образованию маршрутной петли для сетей

получателей из N1 внутри N2.

Сначала обсудим сценарий, приводящий к маршрутным петлям, а затем

причины, вызывающие запуск такого сценария.

Маршрутизатор R1 отправляет маршрутное обновление, содержащие

сети получатели, расположенные в N1, маршрутизатору R2. Маршрутизатор

R2 получает маршрутное обновление, устанавливает маршрут к объявленным

сетям получателям и производит перераспределение полученной маршрутной

информации в протокол маршрутизации RP2, средствами которого затем объ-

являет эти сети получатели своим соседям в N2.

Предположим, что сосед R3 получает маршрутное обновление маршру-

тизатора R2 и устанавливает свои маршруты к объявленным сетям получате-

лям через R2. После этого маршрутизатор R3 сам начинает объявлять данные

сети получатели своим соседям. В конечном итоге это маршрутное обновле-

ние поступает на маршрутизатор R4,который после установки маршрутов к

этим сетям получателям, начинает объявлять их средствами протокола марш-

рутизации RP2 маршрутизатору R2.

Теперь маршрутизатор R2 должен заменить существующие у него

маршруты к этим сетям получателям, указывающие на маршрутизатор R1, на

новые маршруты, указывающие на R4. Поскольку маршрутизатор R1 объявил

их средствами протокола маршрутизации RP1, тогда как маршрутизатор R4

объявляет их средствами PR2, административное расстояние которого мень-

ше чем у PR1.

У этого сценария есть небольшое упущение: маршрутизатор R2 должен

объявить сети получатели, полученные им от маршрутизатора R1 всем своим

соседям практически одновременно. То есть маршрутизатор R4 получить пер-

вое маршрутное обновление, содержащие данные сети получатели, от марш-

рутизатора R2, после чего он должен установить свои маршруты до сетей по-

лучателей в N1 через маршрутизатор R2. С этого момента он должен откло-

269

нять все другие маршрутные обновления, если они имеют метрику, большую

метрики маршрутов, пролегающих через маршрутизатор R2.

Несмотря на это упущение, данный сценарий вполне реален и может

наступить, особенно если этому будут способствовать некоторые дополни-

тельные факторы.

– Маршрутизатор R2 может не отправить маршрутное обновление всем

своим соседям одновременно. Он может запланировать сначала отправку

маршрутной информации маршрутизатору R3 и только после этого маршру-

тизатору R4. Если промежуток времени между передачей маршрутных обнов-

лений маршрутизаторам R3 и R4 достаточно велик, маршрутизатор R4 может

получить маршрутное обновление от другого соседа, в этом случае он объ-

явит сети получатели из N1 маршрутизатору R2, что приведет к установке для

них ложных маршрутов.

– Стоимость канала связи между маршрутизаторами R2 и R4 настолько

велика, что маршрутизатор переключиться на какой-либо другой маршрут,

даже если он перед этим установил маршрут до сетей получателей в N1 через

маршрутизатор R2. Если это произойдет, маршрутизатор произведет объявле-

ние сетей получателей маршрутизатору R2, что приведет к удалению истин-

ных и установке ложных маршрутов маршрутизатором R2.

– Если в какой-то момент времени после первоначального объявления

маршрутной информации о сетях получателях расположенных в N1, произой-

дет временное отключение канала связи между маршрутизаторами R2 и R4,

маршрутизатор R4 установит маршруты до N1 через другого соседа. При

восстановлении канала связи маршрутизатор R4 произведет объявление

маршрутной информации маршрутизатору R2, что приведет к образованию

маршрутной петли.

Это наиболее вероятные факторы, способствующие возникновению

маршрутных петель.

Независимо от того, какие обстоятельства привели к переключению

маршрутов маршрутизатором R2, далее события будут развиваться следую-

щим образом:

1. После изменения маршрутизатором R2 направления маршрутов к се-

тям получателям их N1, он перестает использовать при объявлении этих сетей

метрику назначенную при перераспределении, а вместо нее использует мет-

рику которую он получил от маршрутизатора R4, увеличенную на стоимость

канала связи до маршрутизатора R4. Эта метрика выше, чем метрика полу-

ченная при перераспределении, поскольку она представляет собой эту исход-

ную метрику, увеличенную на стоимость каналов связи между маршрутизато-

рами R3 и R4.

2. Когда маршрутизатор R3 обнаружит увеличение метрики, объявляе-

мой маршрутизатором R2, он замораживает свои маршруты, и начинает объ-

являть эти сети получатели с метрикой, равной бесконечности.

270