Денисов-Винский Н.Д. Mathcad при решении задач по Высшей математики. 1 курс

Подождите немного. Документ загружается.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

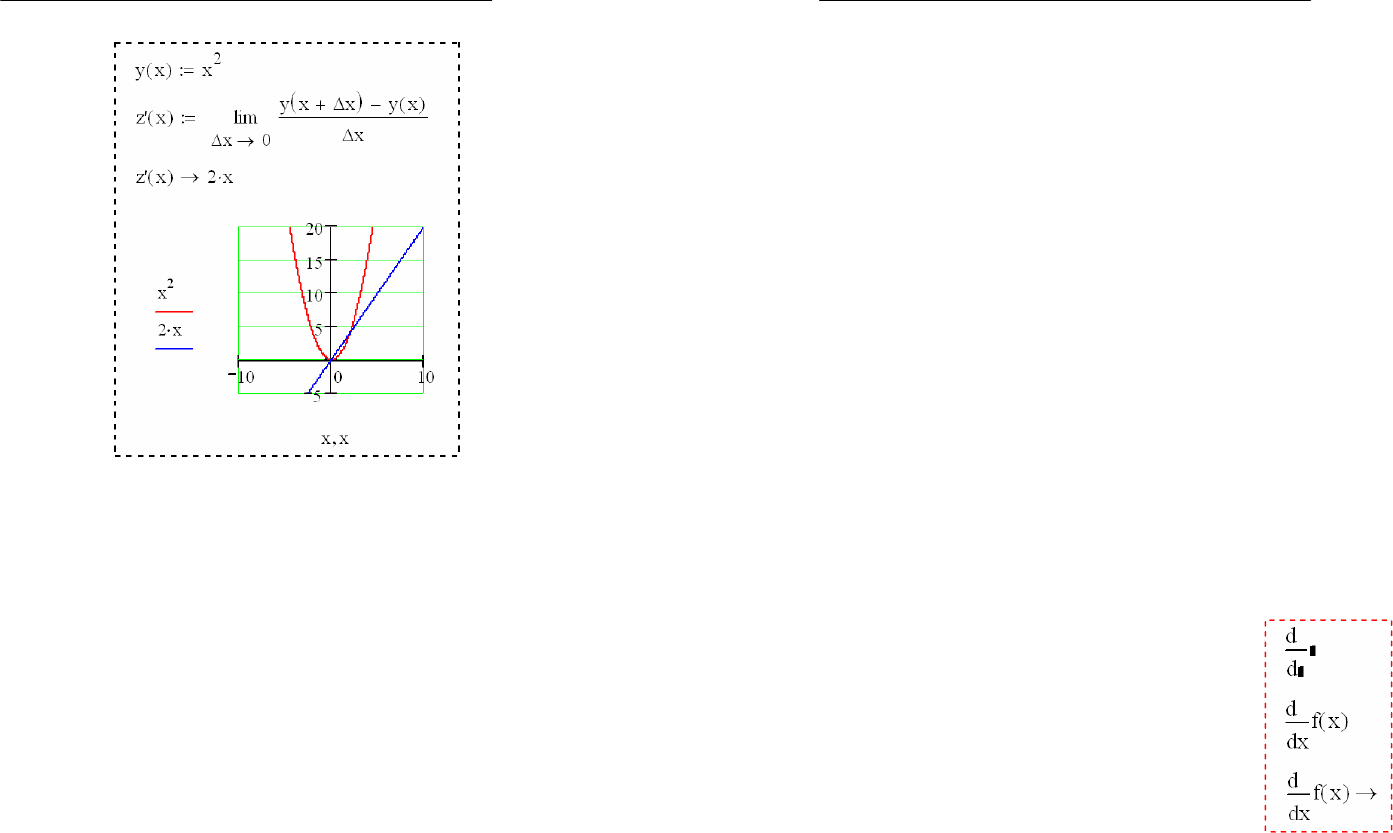
Таким образом, производная непрерывной функции

)(xfy



- это предел, к которому стремиться отношение бес-

конечно малого приращения функции к соответствующему

бесконечно малому приращению аргумента



Если речь идёт о вычислении численного значения произ-

водной, то оно делается в некоторой точке

xx 

. Как извест-

но, значение производной геометрически характеризуется

наклоном касательной в графику

)(xf

в точке

xx 

. Произ-

водную можно рассматривать и как скорость изменения

функции в заданной точке. В экстремумах функций произ-

водная равна нулю.

Помимо производной, часто оперируют понятием диффе-

ренциала:

xxfxdf









)()(

т.е. произведением производной функции на приращение её

аргумента





Если функция имеет производную в точке

xx 

, то она

непрерывная в этой точке. Разрывные функции в точках раз-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

рыва не имеют производных, хотя у них возможны производ-

ные слева и справа от точек разрыва. Непрерывность функ-

ции не является достаточным признаком того, что она имеет

производную. Не все непрерывные функции имеют произ-

водные во всех точках. Существуют непрерывные функции,

вообще не имеющие производных.

Производная от первой производной

(x)f



, т.е. функция

(x)f



, называется производной второго порядка. Могут быть и

производные высшего порядка. Шаблон Mathcad для вычис-

ления производных высшего порядка можно использовать

для вычисления производных до 5-го порядка включительно.

Mathcad вычисляет производные в численном виде адап-

тивным методом Риддера. Он гарантирует 7-8 точных знаков

для первой производной. Вычисление производных высших

порядков – выше пяти – может сопровождаться потерей точ-

ности вычислений и резким возрастанием времени вычисле-

ния. Поэтому лучше всего в этом случае попытаться найти

символьное выражение для производной и затем уже числен-

ное.

8.2 Аналитическое дифференцирование функции

Для того, чтобы аналитически найти производную функ-

ции в Mathcad необходимо – задать в любом

свободном месте окна документа функцию

одной переменной (при этом необходимо

помнить о правилах ввода идентификатора,

т.е. имени на саму функцию и переменную в

этой функции), к примеру:

2:f(x)

 xxx

; после чего вызвать с па-

нели Матанализ оператор Производная. В

данном операторе есть два черных квадрати-

ка, куда необходимо будет вписать имя функции – т.е. её

идентификатор и переменную, от которой она зависит, а так-

же переменную функции, по которой происходит дифферен-

цирование. Таким образом, в черный квадратик около гори-

зонтальной строки вписывается имя функции с переменной, в

черный квадратик под горизонтальной строкой вписывается

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

переменная, по которой происходит дифференцирование.

В данном случае запись символа вычисления производной в

системе Mathcad ни

чем не отличается от традиционного обозначения вычисления

производной в математике. Для того, чтобы вычислить значе-

ние производной – т.е. найти это значение в символьном ви-

де, необходимо после оператора диффе-

ренцирования указать оператор Симво-

лический знак равенства, который

располагается на панели Вычисления.

После чего будет вычислено значение производной в симво-

лическом виде.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Как правило, возникает необходимость не просто вычис-

лить производную от какой-то заданной функции, а задать

функцию, которая является производной от заданной. В этом

случае можно результат вычисления производной – как пра-

вило, результатом также является функция от заданной пере-

менной, присвоить какой-то функции, которая и будет яв-

ляться производной от заданной. К ней будут применимы все

свойства и операции, которые возможны над функциями в

Mathcad.

Во многих случаях при вычислении символьной про-

изводной от какой-то достаточно большой функции символь-

ный процессор Mathcad не упрощает полученное выражение.

Например, при вычислении производной по слагаемым не

приводит ответ к общему знаменателю, что усложняет пони-

мание ответа дифференцирования. Для того, чтобы упростить

получившийся результат дифференцирования (этот способ

может применяться не

только при операции

дифференцирования, а

просто – как способ

приведения к общему

знаменателю) необхо-

димо вызвать команду

simplify, которая рас-

полагается на панели

Символы. В левый

черный квадратик не-

обходимо вписать либо

выражение, либо функ-

цию, которая была за-

дана ранее. После чего оператор с права от себя, после стре-

лочки, выдаст готовый результат.

Необходимо напомнить, что в описанном применении

оператора дифференцирования его результатом является

функция той же переменной

Исходная функция сможет зависеть не только от аргумен-

та

, но и от других аргументов, например

),,,( tzyxf

и т.п. В

этом случае дифференцирование производится точно так же,

причём становится более понятной необходимость определе-

ния переменной дифференцирования (в нижнем местозапол-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

нителе оператора дифференцирования). Расчёты производных

по разным аргументам (в этом случае говорят от частных

производных), разумеется, будут давать совершенно разные

результаты.

8.3 Вычисление производной в точке

Помимо того, что зачастую бывает необходимо считать

производную в общем виде, иногда бывает достаточно знать

значение (т.е. численное значение) этой производной в какой-

то заданной точке.

Для того чтобы рассчитать про-

изводную в точке, необходимо пред-

варительно задать значение аргу-

мента в этой точке. Результатом

дифференцирования в этом случае

будет число — значение производ-

ной в этой

точке. Ес-

ли резуль-

тат удается

отыскать

аналитиче-

ски, то он приводится в виде число-

вого выражения, а для того, чтобы

получить его в форме числа, доста-

точно ввести после выданного вы-

ражения символ числового равенст-

ва «=».

Однако для того, чтобы продифференцировать функцию,

вовсе необязательно предварительно присваивать её какое-

либо имя. Можно определить функцию непосредственно в

операторе дифференцирования.

Ещё раз напомним, что оператор дифференцирования, в

основном, соответствует его общепринятому математическо-

му обозначению, и поэтому его легко использовать интуи-

тивно. Однако в некоторых случаях при вводе оператора

дифференцирования следует проявить осторожность. Рас-

смотрим один показательный пример, который демонстриру-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

ет неправильное применение оператора дифференцирования

для вычисления производной в точке. Вместо вычисления

производной sin(x) при х=2, как этого можно было ожидать,

получено нулевое значение. Это случилось из-за того, что

аргумент функции sin(x) введен не в виде переменной х, а в

виде числа. Поэтому Mathcad воспринимает последнюю стро-

ку как вычисление сначала значения синуса в точке х=2, а

затем дифференцирование этого значения (т. е. константы)

также в точке х=2, в соответствии с требованием первой

строки листинга. Поэтому ответ, на самом деле, неудивителен

— в какой точке ни дифференцируй константу, результатом

будет ноль.

8.4 Дифференцирование в точке

Для того, чтобы численно продифференцировать функ-

цию

f(x)

в некоторой точке, следует использовать оператор

численного вывода (вместо символьного).

Необходимо – определить точку

xx 

, в которой будет

вычислена производная, например

1.0



; далее необходимо ввести

оператор дифференцирования и

обычным образом ввести имя

функции и аргумента на места

черных квадратиков; ввести опе-

ратор численного результата «=».

Необходимо помнить об опре-

делении точки, в которой производится численное дифферен-

цирование – в противном случае будет выдано сообщение об

ошибке, гласящее, что переменная или функция, входящая в

выражение, ранее не определена. Между тем, символьное

дифференцирование не требует обязательного явного задания

точки дифференцирования. В этом случае вместо значения

производной (числа или числового выражения) будет выдана

аналитическая зависимость.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

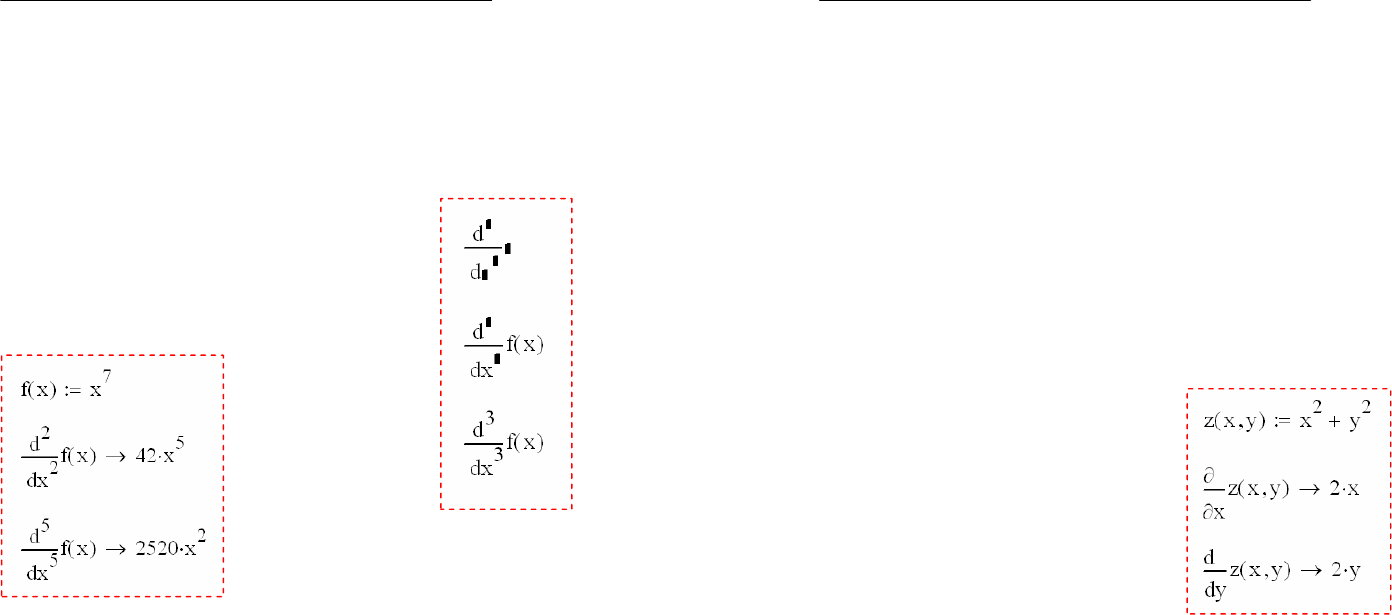
8.5 Производные высших порядков

Mathcad позволяет численно определять производные

высших порядков, от 3-го до 5-го включительно. Чтобы вы-

числить производную функции

f(x)

N-го порядка в точке х,

нужно проделать те же самые действия, что и при взятии пер-

вой производной, за тем исключением, что вместо оператора

Производная необходимо применить опера-

тор Производная N-го порядка. Этот опера-

тор вводится с той же панели Calculus (Вы-

числения), и содержит еще два дополни-

тельных местозаполнителе, в которые следу-

ет поместить число N. В полном соответст-

вии с математиче-

ским смыслом опе-

ратора, определе-

ние порядка произ-

водной в одном из

местозаполнителе

(черненький квад-

ратик) приводит к автоматическому

появлению того же числа в другом

из них.

Очевидно, что "производная"

при N=0 по определению равна самой функции, при N=1 по-

лучается обычная первая производная. Обратите внимание,

что, как и при вычислении обычной производной, необходи-

мо перед оператором дифференцирования присвоить аргу-

менту функции значение, для которого будет вычисляться

производная. А вот для аналитического нахождения произ-

водных высших порядков при помощи оператора символьно-

го вывода, вводить значения аргумента не следует.

Необходимо помнить, что численный метод предусмат-

ривает возможность вычисления производных до 5-го поряд-

ка, а символьный процессор умеет считать производные про-

извольного порядка (конечно, если аналитическое решение

задачи в принципе существует).

Чтобы вычислить производную порядка выше 5-го чис-

ленно, можно последовательно применить несколько раз опе-

ратор N-й производной. Однако следует помнить о том, что

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

численное определение производных высших порядков про-

изводится тем же вычислительным методом Риддера, что и

для первых производных. Поскольку, как уже было сказано,

для первой производной этот метод обеспечивает точность до

7—8 значащих разрядов числа, при повышении порядка про-

изводной на каждую единицу точность падает примерно на

один разряд.

8.6 Частные производные

Как уже было отмечено выше, подавляющее большинство

функций зависят не от одной, а от многих переменных. Для

того, чтобы исследовать функцию, которая зависит от многих

переменных необходимо исследовать её по каждой перемен-

ной, при этом остальные переменные принимать как констан-

ты. Отсюда и вытекает понятие част-

ной производной.

Частные производные вычисляет-

ся в Mathcad таким же образом, как и

обычные производные. Необходимо

задать функцию нескольких пере-

менных, и в нижнем черном квадра-

тике указать по какой переменной

необходимо вычислить производную.

Для того чтобы изменить вид

оператора дифференцирования на представление частной

производной, следует: Вызвать контекстное меню из области

оператора дифференцирования нажатием правой кнопки мы-

ши; выбрать в контекстном меню верхний пункт View De-

rivative As (Показывать производную как); в появившемся

подменю выбрать пункт Partial Derivative (Частная произ-

водная).

8.7 Построение асимптоты графика функции

Асимптотой графика функции называется прямая, рас-

стояние до которой от точки, лежащей на графике, стремить-

ся к нулю при неограниченном удалении от начала координат

этой точки по графику.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Асимптоты могут быть вертикальными, наклонными и

горизонтальными.

Говорят, что прямая



является вертикальной асим-

птотой графика функции

)(xfy



, если





)(lim xf

Уравнение наклонной асимптоты будем искать в виде

bkxy





Необходимо найти численное значение коэффициентов

уравнения прямой

bkxy





Данные коэффициенты находим согласно выражениям:

)(

lim









kxxfb





)(lim

Таким образом, если для функции

)(xfy



существует

асимптота, то коэффициенты

для уравнения прямой

bkxy





находятся

согласно этим фор-

мулам.

Если хотя бы

один из пределов не

существует или равен

бесконечности, то

кривая

)(xfy



на-

клонной асимптоты

не имеет.

В частности, если



, то

)(lim xfb

x 



Поэтому



- урав-

нение горизонталь-

ной асимптоты.

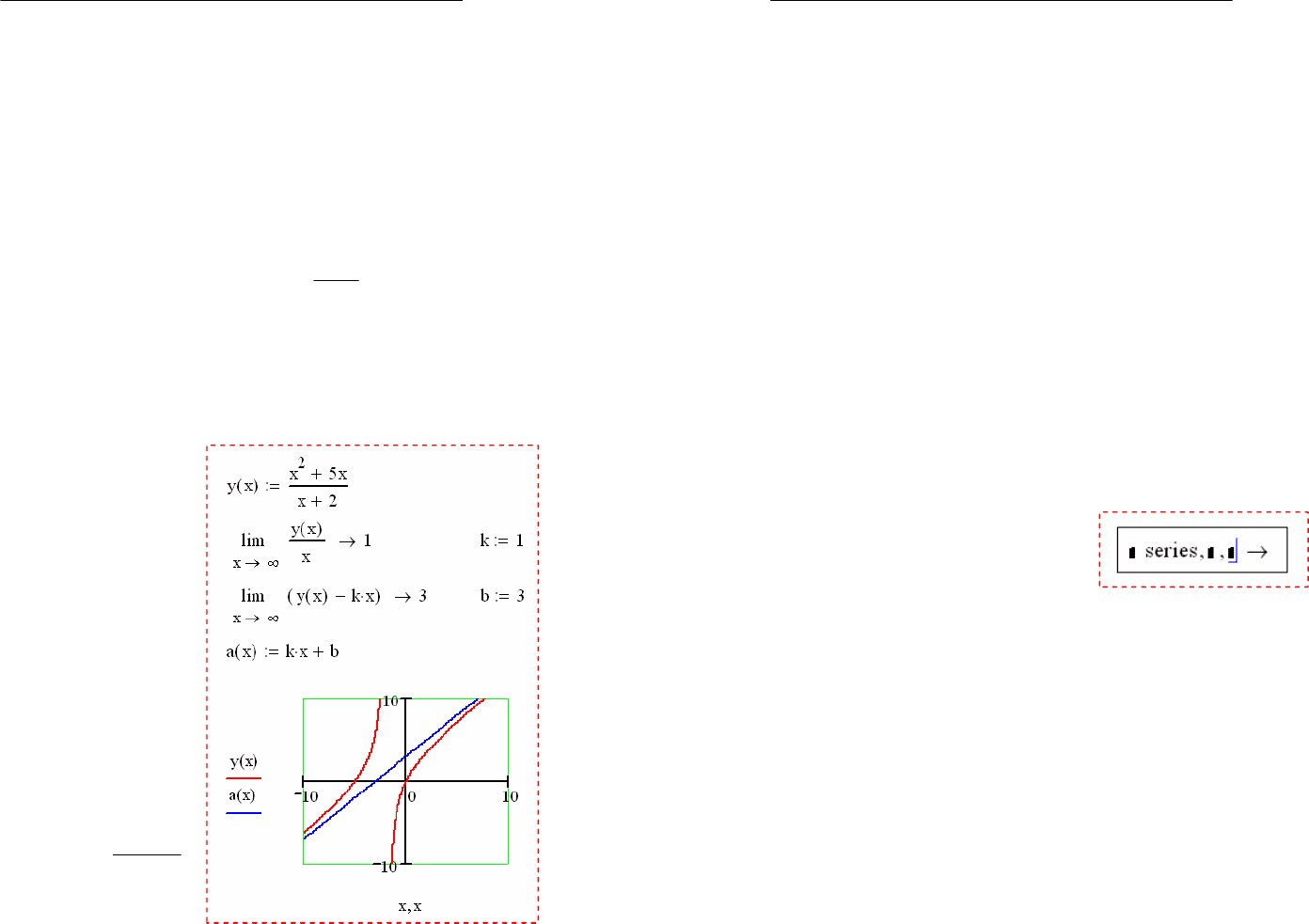
Пусть дана функ-

ция

:y(x)





Построим для неё

асимптоту.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

8.8 Формула Тейлора, Маклорена и

разложение элементарных функций

Формула Тейлора служит для приближения функции

f(x)

многочленом Тейлора. Как правило, достаточно взять 4-5 сла-

гаемых, чтобы ошибка приближения (остаточный член) стала

незначительной в небольшой окрестности заданной точки

Формула Тейлора при



, называется формулой Мак-

лорена. Эти формулы используются в прикладных програм-

мах и калькуляторах для вычисления значений элементарных

функций с большой точностью.

Команда Expand to Series (разложить в ряд) выполняет

разложение выражения в ряд Тейлора относительно выделен-

ной переменной с заданным по запросу числом членов ряда

(число определяется по степеням ряда). По умолчанию задано



. Разложение возможно для функции заданной перемен-

ной. В разложении указывается остаточная погрешность раз-

ложения. Эта команда даёт разложение в ряд в точке



именуемое также рядом Маклорена.

Для того, чтобы разложить заданную функцию в ряд

Маклорена, необходимо вызвать с

панели Символы вызвать команду

Символ разложить последова-

тельно, который на панели ещё

называется как series.

В левый черный квадратик, который находится слева от

символа команды series необходимо вписать функцию, кото-

рую необходимо разложить. Её можно списать туда непо-

средственно, либо вписать название функции, которая была

задана ранее вместе с переменными этой функции. В правый

черный квадратик, который следует непосредственно за клю-

чевым словом series необходимо вписать переменную, отно-

сительно которой будет разложена заданная функция. В са-

мый крайний правый черный квадратик необходимо вписать

количество членов разложения.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

В ряде случаев необходимо не просто получить результат,

записать его в функцию – таким образом надо задать функ-

цию относительно той переменной, относительно которой

необходимо разложить функцию.

IX. Построение графиков

функций в пространстве

9.1 Общие положения

В старых версиях Mathcad при построении графика по-

верхности, представленной функцией

y)z(x,

двух перемен-

ных, приходи-

лось предварительно определять матрицу

аппликат (высот

) её точек. Разумеется, этот способ возможен и более позд-

них версиях Mathcad.

Поскольку элементы мат-

рицы

- индексированные

переменные с целочисленны-

ми индексами, то перед созда-

нием матрицы требуется за-

дать индексы в виде ранжиро-

ванных переменных с цело-

численными значениями, а за-

тем уже из них формировать

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

сетку значений

- и

- координат для аппликат

y)z(x,

. Зна-

чения

при этом обычно должны быть вещественными

числами, нередко как положительными, так и отрицательны-

ми.

Всё это приводит к усложнению алгоритма подготовки

данных для построения трехмерного графика поверхности,

особенно большие трудности это вызывает у студентов – они

не всегда понимают, зачем все эти сложности и как задать

область изменения

, чтобы была построена нужная

часть поверхности.

После того, как была определена функция, график, а точ-

нее поверхность, которую надо построить, необходимо задать

ранжированные переменные. Как правило, их обозначают

через буквы

, которые, если вспомнить курс аналитиче-

ской геометрии, являются ортами координат

. Предел

этих переменных зависит от того, насколько точно пользова-

тель хочет построить поверхность (здесь уместна аналогия с

графиком функции на плоскости, где «плавность» кривой за-

висела от того, какой диапазон будет определён для ранжиро-

ванной переменной). Однако необходимо помнить, что чем

больше будет установлен предел для ранжированной пере-

менной, тем дольше система будет «думать» прежде чем изо-

бразить данную поверхность. Необходимо также учесть, что

поверхность, которая будет построенная Mathcad можно вра-

щать на шаблоне относительно произвольной оси, с целью её

«рассмотрения» со всех сторон. В этом случае также процесс

вращения будет затягиваться из-за того, что система будет

пересчитывать множество точек, количество которых напря-

мую зависит от пределов ранжированных переменных.

После задания ранжированных переменных необходимо

задать матрицу – имя матрицы должно соответствовать всем

правилам задания идентификатора. Для матрицы устанавли-

ваем нижние индексы – первый индекс, как правило, отвечает

за ось

, а второй за ось

- хотя порядок оси также в боль-

шинстве случаев зависит от пользователя. Далее в матрицу

записываем значения функции при всех возможных сочета-

ниях ранжированных переменных.

После указанных выше действий командой График по-

верхности с меню Графики вводится шаблон графика, левый

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

верхний угол которого помещается в место расположения

курсора. Шаблон, в свою очередь, содержит единственное

место ввода – темный прямоугольник у левого нижнего угла

основного шаблона. В него необходимо имя матрицы аппли-

кат поверхности. После этого надо установить указатель мы-

ши в стороне от графического блока и щелкнуть левой кноп-

кой.

В данном случае построена поверхность в виде «прово-

лочного каркаса» со всеми видимыми линиями. В данном

случае от ранжированных переменных зависит, насколько эта

сетка будет гуще или реже.

Наглядность представления поверхностей и трехмерных

фигур зависит от множества факторов: масштаба построений,

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

углов поворота фигуры относительно осей, применения алго-

ритма удаления невидимых линий или отказа от него, исполь-

зование функциональной окраски и т.д.

Применение алгоритма невидимых линий делает рисунок

более наглядным. Дальнейшее повышение наглядности вос-

приятия трехмерных графиков обеспечивается применением

функциональной окраски. По существу она даёт дополни-

тельную информацию о третьем измерении.

С помощью команд изменения формата можно получить

множество разновидностей трехмерной графики. В частно-

сти, возможен вывод координатных осей, «параллелепипеда»,

обрамляющего фигуру, и иных деталей подобных графиков,

например титульных надписей.

Поскольку график строится на основе матрицы, содержа-

щей только координаты высот фигуры, то истинные масшта-

бы по осям

неизвестны и на рисунках не проставляют-

ся. Возможно, впрочем, выводить порядковые номера эле-

ментов матриц в заданном направлении. Необходимо следить

за тем, как сформировать векторы

, чтобы фигура вы-

глядела естественно и была видна нужная часть фигуры в

пространстве. Все это несколько затрудняет быстрое создание

графиков трехмерных поверхностей нужного вида.

9.2 Построение параметрически

заданных поверхностей

Большие возможности даёт несколько иной способ зада-

ния поверхностей – в параметрическом виде. При этом при-

ходится формировать три матрицы,

, и указывать их

в шаблоне в виде





ZY,X,

. В этом случае скобки необходимы,

поскольку в противном случае Mathcad попытается построить

три поверхности по данным матриц

В данном случае параметрический способ построения

объемных тел позволяет без особых затруднений перейти как

в сферическую, так и в цилиндрическую систему координат.

В этом случае все координаты зависят от одной переменной,

которая является параметром. При обычном способе построе-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

ния поверхностей необходимо задавать зависимость коорди-

наты

, как функцию от двух других координат

9.3 Построение трёхмерных фигур с вырезом

Параметрическая форма задания трехмерных фигур от-

крывает ещё одну возможность – представление объемных

фигур с вырезом. Такие фигуры отличаются повышенной на-

глядностью, ибо в вырезе видна внутренняя структура фигур.

Всё что надо для этого построения, - ограничить диапазон

изменения параметрических углов, сделав его меньше обыч-

ного значения



автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

9.4 Построение трехмерных графиков

без задания матрицы

Последние версии системы Mathcad обладает принципи-

ально новой возможностью – допускается построение трёх-

мерных графиков без задания матрицы аппликат поверхно-

сти. В результате построение графиков поверхностей выпол-

няется так же просто, как и построение двумерных графиков.

В данном случае для построения достаточно задать функ-

цию двух переменных и указать её имя (необходимо указать

именно имя функции – т.е. её идентификатор, без указания

входящих в неё переменных) в месте ввода шаблона графика.

Единственным недостатком такого упрощенного метода по-

строения поверхностей является неопределённость в масшта-

бировании, поэтому для получения приемлемого вида графи-

ка требуется форматирование. Впрочем, в любом случае по-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

лучение графика достаточно эффективном виде всегда требу-

ет его форматирования.

9.5 Построение графика поверхности,

заданной в векторной параметрической форме

Описанный выше метод быстрого построения поверхно-

сти может иметь множество вариантов. Один из них – зада-

ние поверхности в векторной параметрической форме.

Данный способ задания графика – называется матричным.

В нём фигурирует две переменные, а каждая строка матрицы

отвечает за свою координату.

Для создания исходного графика не требуется никаких

промежуточных операций. Вид графика можно улучшить пу-

тём форматирования графика мышью.

Для того, чтобы с простотой пользоваться всевозможны-

ми функциями Mathcad для построение фигур и поверхностей

в пространстве, необходимо достаточно уверенно владеть ма-

тематическим аппаратов, в частности таким понятиями как

цилиндрическая система координат, сферическая система ко-

ординат, переход о одной системы координат к другой, - ка-

кой вид имеют те или иные уравнения кривых в пространстве

– в частности шар, эллипсоид, гиперболоид и т.п.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

X. Примеры решения контрольной

работы по математике в Mathcad

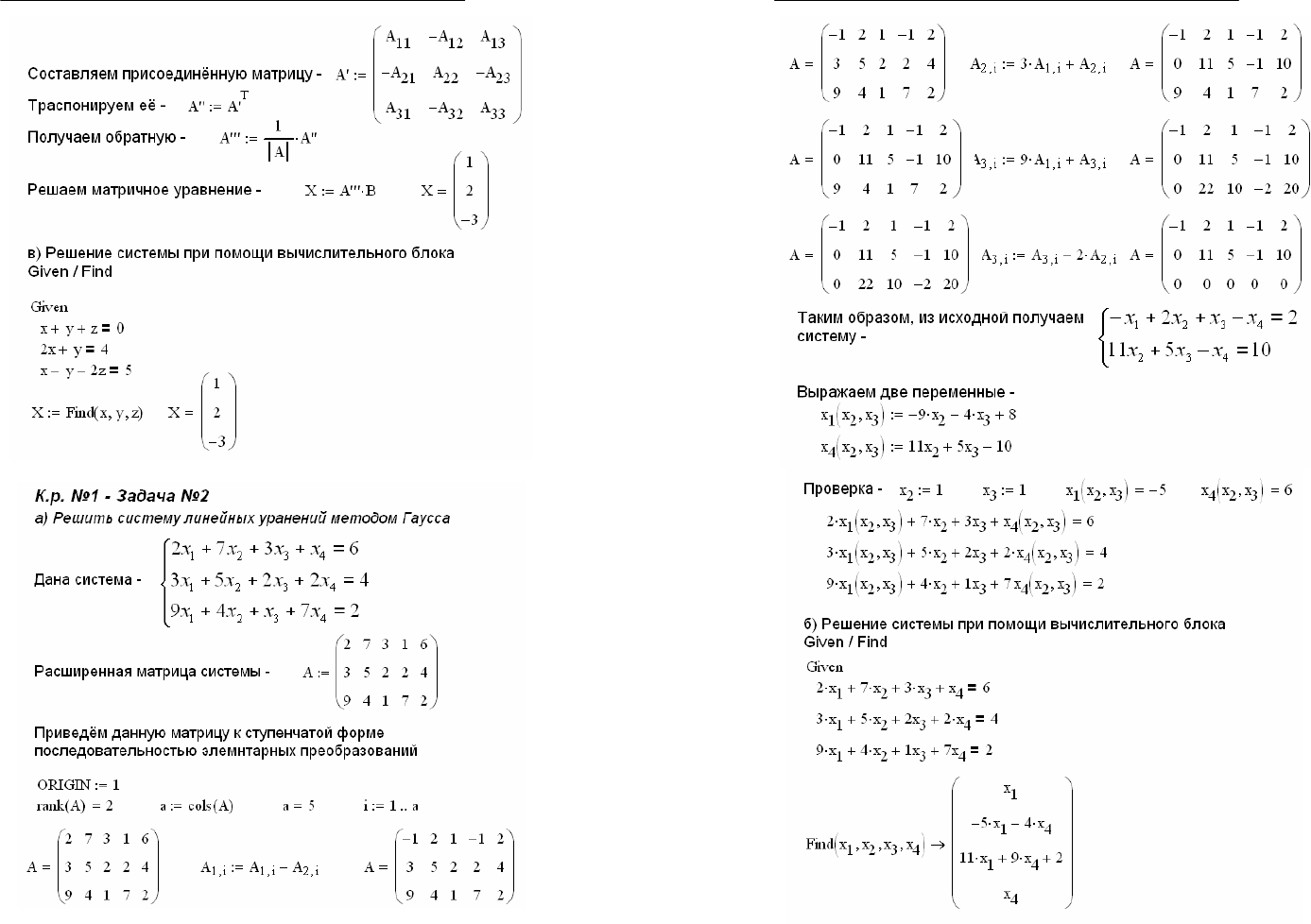
автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru