Денисов-Винский Н.Д. Mathcad при решении задач по Высшей математики. 1 курс

Подождите немного. Документ загружается.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru



; данной свойство справедливо для всех функций в сис-

теме Mathcad;

• Функция last(V) - возвращает номер последнего эле-

мента (только для вектора);

для вектора

получаем -

2last(V1)



; собственно го-

воря, эта функция выводит номер индекса последнего эле-

мента вектора;

• Функция max(V) - возвращает максимальный по зна-

чению элемент вектора или матрицы;

для вектора

получаем -

9max(V1)



; для матрицы

получаем -

9max(M1)



;

• Функция min(V) - возвращает минимальный по значе-

нию элемент вектора или матрицы;

для вектора

получаем -

3min(V2)



; для матри-

цы

получаем -

1min(M1)



;

• Функция identity(n) - создаёт единичную матрицу по-

рядка

; например, для



получаем

)identity(2:E1



, что















• Функция augment(M1,M2) - объединяет в одну две

матрицы

, имеющие одинаковое число строк (объе-

динение идёт по горизонтали); также данная функция может

объединить и два вектора, порядок которых совпадает, в ре-

зультате получится матрица с числом столбцов равно двум и

числом строк, равное числу строк этих векторов; (при ис-

пользовании этой функции необходимо помнить, что число

строк у объединяющих матрицах должно быть равно);

например -

V2),augment(V1:Vaug



, получаем такой ре-

зультат -















Vaug

;

• Функция stack(M1,M2) – объединяет «по вертикали»

две матрицы

, имеющее одинаковое число столбцов;

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

• Функция submatrix(A, ir, jr, ic, jc) – возвращает под-

матрицу, состоящую изо всех элементов, содержащих в стро-

ках с

по

и столбцов с

по

, причём должно выпол-

няться условие (

jrir



jcic



);

Пример -

)M1,0,1,0,1submatrix(:R



, получаем, что















;

• Функция diag(V) - создаёт диагональную матрицу,

элементы главной диагонали которой равны элементам век-

тора

;

2.6 Функции, возвращающие специальные

характеристики матриц

Следующие функции возвращают специальные характе-

ристики матриц:

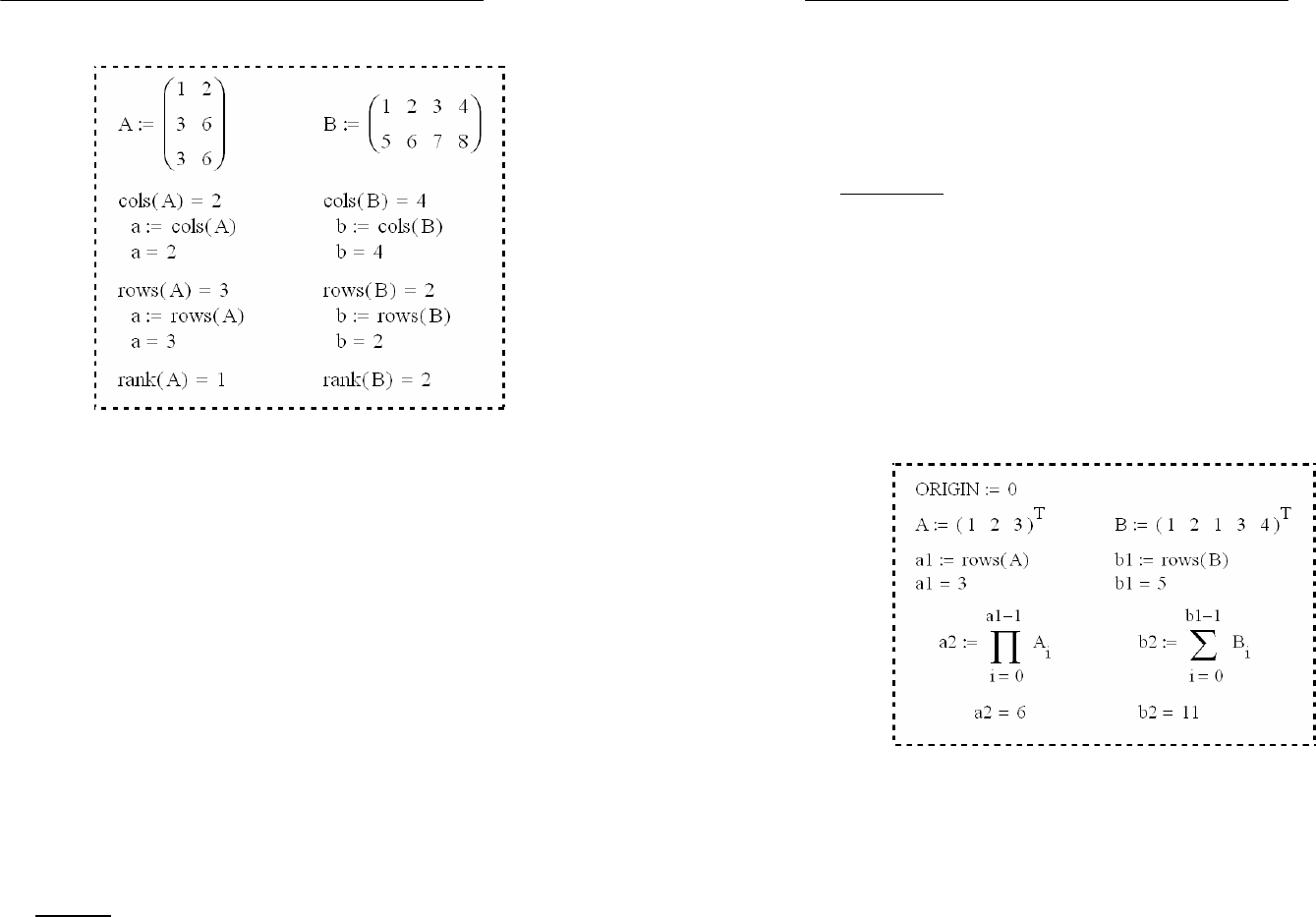
• Функция cols(M) – возвращает число столбцов матри-

цы

;

Обратите внимание на термин «функция возвращает».

Данный термин применяется для всех языков программиро-

вания. Как правило, программа обращается к функции с ка-

ким-либо числом или набором чисел – массивом. В ответ на

обращение функция возвращает как-либо результат вычисле-

ния - в нашем случае число.

• Функция rows(M) – возвращает число строк матрицы

;

• Функция rank(M) – возвращает ранг матрицы

;

• Функция sort(V) – сортировка элементов вектора в по-

рядке возрастания их значения;

Для решения некоторых задач в курсе электротехники и

при выполнении курсового проекта необходимо будет для

достаточно больших векторов или матриц найти сумму или

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

произведение всех или некоторых элементов векторов или

матриц.

Пусть дан вектор

. Необходимо найти сумму и произ-

ведение всех его элементов. При этом необходимо помнить,

что данный вектор может получаться при решении какой-то

задачи. К примеру, порядок этого вектора определяется ка-

ким-то выражением и записывается в переменную

. Т.е.

есть число, соответствующее количеству элементов в этом

векторе. (Когда какие-то параметры задачи задаются в неяв-

ном виде – т.е. через переменные, значения которых будет

определяться из условия конкретной задачи, то такая задача

называется – задача в общем виде). Таким образом, порядок

вектора

может быть сколь угодно большой, и найти сум-

му или произведение его элементов «в ручную» будет очень

сложно.

Для решения этой задачи в Mathcad предусмотрена функ-

ция Суммирование и Произведение, которые находятся на

панели Матанализ. При этом, как и в любой другой функ-

ции, значения этих функций может быть, а в подавляющем

случае и должно, записано в какую-то переменную.

Пример – пусть дан вектор















:V1

. Необходимо най-

ти сумму и произведение его элементов. В этом случае запи-

сываем:

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru





1-n

V1:summa_V1 ,

5summa_V1



;





1-n

V1:ie_V1proizveden ,

6ie_V1proizveden



;

Замечания:

• Символ подчёркивания “_” также очень часто применя-

ется в названиях переменных. Его основная функция – это

функция пробела. Напомним, что в идентификаторе, т.е. име-

ни переменной пробелов быть недолжно.

• Переменная

содержит в себе количество элементов

вектора. При этом индексация элементов вектора начинается

не с «1», а с «0». Поэтому в цикле для Суммы и Произведе-

ния необходимо задать переменную «



», но это только в

том случае, если мы ходим начинать суммировать или умно-

жать с первого элемента, который имеет индекс «0».

• В векторе

мы задаём индекс, по которому будет

осуществляться доступ к данным вектора (или в общем слу-

чае массива)

Таким образом, суммирование или произведение элемен-

тов вектора происходит следующим образом. Оператор берёт

первый элемент с индексом «



», т.е.

, равный какому-

то числу, суммирует или умножает его со следующим эле-

ментом данного вектора

, поле чего действие повторяет до

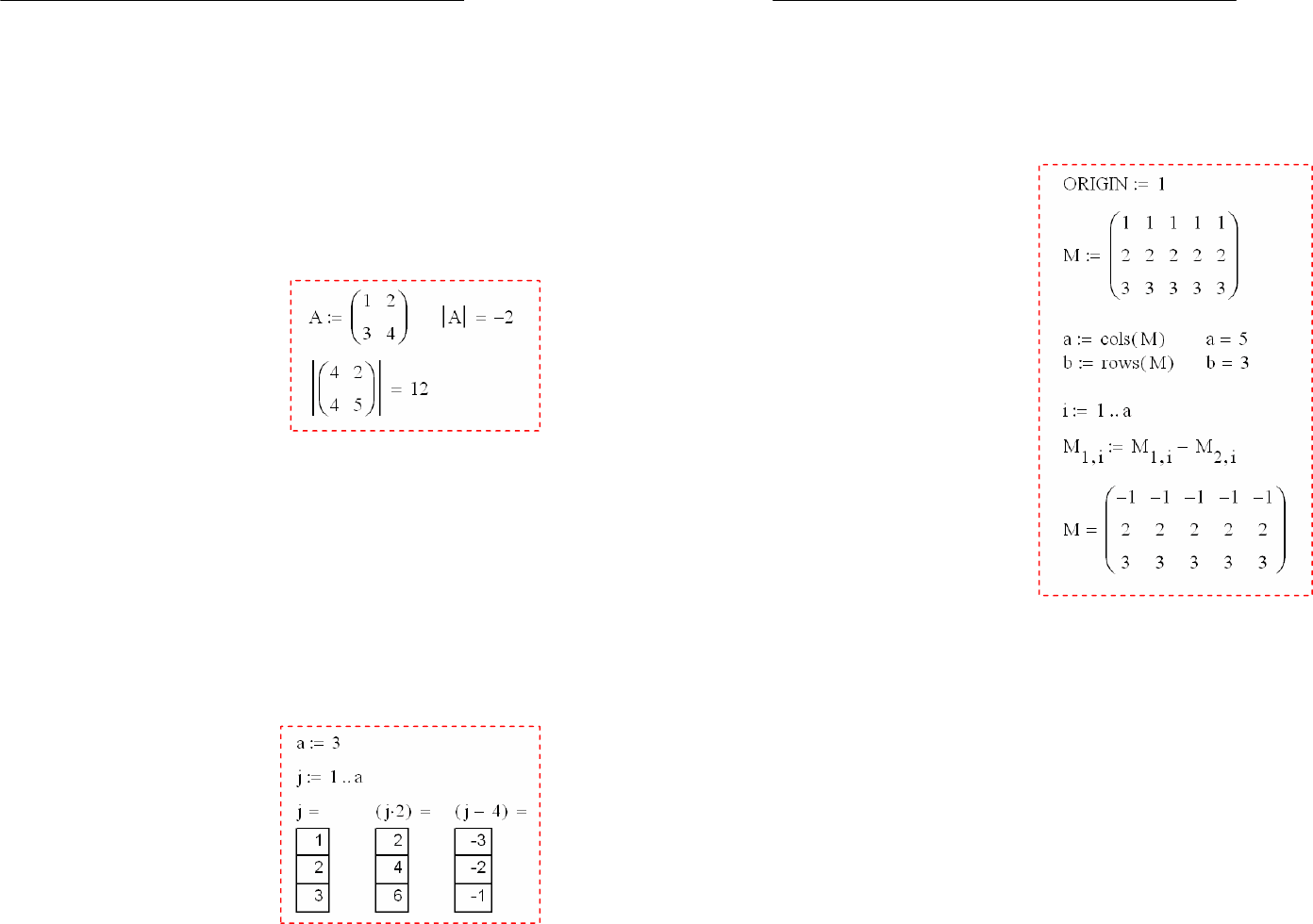
автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

тех пор, пока оператор не прейдет к элементу «

». Резуль-

тат этого сложения или умножения записывается в перемен-

ную, которая стоит перед этим оператором.

При решении задач в общем виде, когда порядок вектора

есть величина переменная, данный способ вычисления (ум-

ножения или суммирование элементов матрицы или вектора)

очень удобен. То же самое относится и к матрицам.

2.6 Вычисление определителя матрицы

Напомним, что каждой

квадратной матрице порядка

можно поставить в соответст-

вие число, называемое опреде-

лителем (обозначается

det(A)

или



Система Mathcad предос-

тавляет возможность вычислять определитель квадратной

матрицы. На панели Матрицы находиться кнопка Вычисле-

ние определителя. Можно непосредственно ввести матрицу

и найти значение определителя, либо задать матрицу в пере-

менную и вычислить определитель от переменной.

2.7 Элементарные преобразования матриц

Напомним, что к элементарным преобразованиям отно-

сятся преобразования следующих типов:

• замена местами двух параллельных рядов матрицы;

• умножение всех эле-

ментов ряда матрицы на

число не равное нулю;

• прибавление (поэле-

ментно) к ряду матрицы

другого параллельного

ряда, умноженного на

число.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

На панели Матрицы находиться кнопка Задать диапазон

дискретной величины, которая позволяет в автоматическом

режиме проходить по элементам вектора или матрицы. Таким

образом, данная команда организует своеобразный цикл с

заданным шагом (по умолчанию шаг равен “1”).

Для задания Диапазона дискретной величины задаётся

переменная, например

ставиться Оператор при-

своения -



, после чего

вызывают оператор Задать

диапазон дискретной ве-

личины – куда в «черные

квадратики» записывается

начало диапазона и его ко-

нец. Таким образом, органи-

зуется цикл по заданному

промежутку.

Для того, чтобы осуще-

ствлять элементарные пре-

образования над матрицами

необходимо задать диапазон

для дискретной величины –

как правило это количество

строк или количество столб-

цов и при помощи операто-

ра присвоения осуществить необходимые преобразования над

элементами строк или столбцов – вычитая, складывая или

умножая на число поэлементно.

2.8 Задание векторов в системе Mathcad

Из курса векторной алгебры известно, что вектор – это

направленный прямолинейный отрезок, т.е. отрезок, имею-

щий определенную длину и определенное направление. Та-

ким образом, чтобы задать вектор на одномерной системе ко-

ординат – на прямой, двумерной системе координат – на

плоскости или трёхмерной системе координат – в простран-

стве, необходимо знать его проекции. Проекции вектора в

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

общем случае можно получить, зная координаты точки нача-

ла и конца вектора. Как правило, координаты точки задаются

радиус-вектором





zyxr ;;

или

kzjyixr 



, где

единичные векторы (орты), выделенные на координатных

осях

соответственно.

В теории линейной алгебры есть так называемая основная

формула векторного исчисления, которая имеет вид

kajaiaa

zyx





и представляет собой разложение век-

тора по ортам координатных осей. Числа

называ-

ются координатами вектора

, т.е. координаты вектора -

проекция на соответствующие координатные оси. Именно

координаты вектора характеризуют его ориентацию в про-

странстве (на плоскости, на прямой) и определяют его длину.

Координаты вектора также можно найти, зная координа-

ты точек конца и начала вектора. Пусть даны координаты

двух точек





111

;; zyxA





222

;; zyxB

. Тогда координаты векто-

ра

имеют вид













kzzjyyixxAB 

121212



В Mathcad векторы являются частным случаем матриц, и

поэтому для них справедливы те же операции, что и для мат-

риц. Вместе с тем для векторов в линейной алгебре преду-

смотрен целый ряд специальных операций, и все они реали-

зованы в системе Mathcad.

Пусть вектор

задан

своими координатами

kjiAB  321



. Для того,

чтобы задать данный вектор в

системе Mathcad и чтобы для

него были доступны все опе-

рации векторной алгебры, необходимо создать матрицу, со-

стоящую из одного столбца и трёх строк (для трёхмерной

системы координат; для двумерной системы координат, т.е.

если вектор задан на плоскости, необходимо создать матрицу,

состоящую из одного столбца и двух строк; если вектор задан

на прямой – т.е. в одномерной системе координат, то необхо-

димо создать матрицу, состоящую из одного столбца и одной

строки; в общем случае для, к примеру, двумерной системы

координат можно задать матрицу, состоящую из одного

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

столбца и трёх строк, но при этом проекция вектора на ось

будет нулевой).

Важно!!! Необходимо помнить, что все векторы в систе-

ме Mathcad задаются именно матрицей столбцом. Если вектор

будет задан матрицей строкой, то после задания матрицы не-

обходимо поставить операцию транспонирования – в против-

ном случае Mathcad не сможет работать с этой матрицей как с

вектором.

В теории линейной алгебры широко применяются вектора

n-мерного пространства. В этом случае размер матрицы

столбца – т.е. количество строк в матрице зависит от того, в

каком n-мерном пространстве задаётся вектор. В этом случае

бывает удобно записать вектор как транспонированную мат-

рицу строку.

2.9 Линейные операции над векторами

Под линейными опе-

рациями над векторами

понимают операции сло-

жения и вычитания век-

торов, а также умножение

вектора на число. В этом

случае линейные опера-

ции над векторами ни чем

не отличаются от линей-

ных операций над матрицами.

Однако должно выпол-

няться условие – вектора, над

которыми выполняется сложе-

ние или вычитание должны

быть одинакового размера.

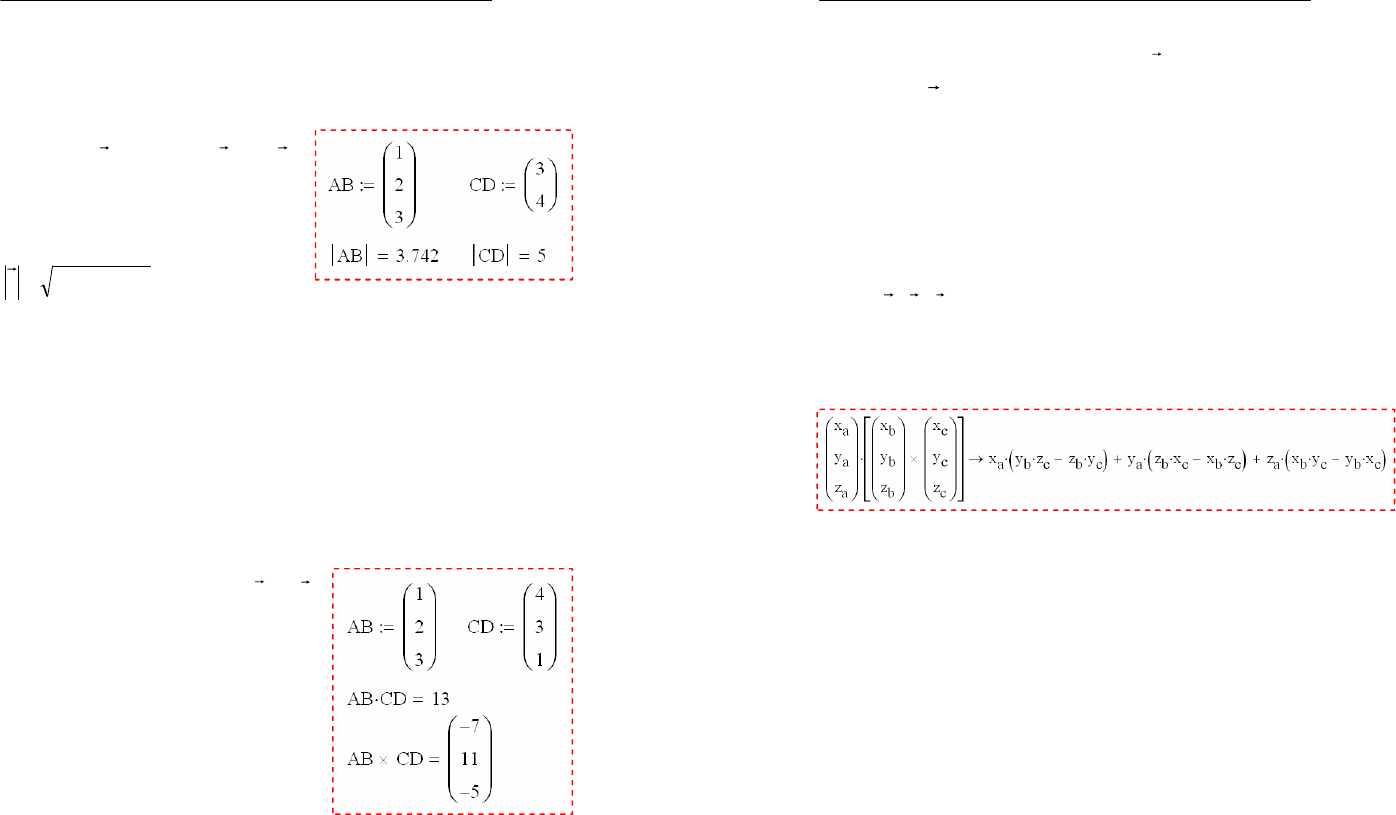
автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

2.10 Длина вектора

Как известно вектор характеризуется не только направле-

нием, но и длиной. Пусть дан

вектор

kajaiaa

zyx





Тогда соответственно

- его координаты и длина его

находится по формуле:

222

zyx

aaaa 

Для того, чтобы найти длину вектора, заданного матри-

цей, в Mathcad необходимо воспользоваться командой Мо-

дуль с панели Арифметика или командой Вычисление оп-

ределителя с панели Матрицы. Однако чтобы не путаться –

лучше пользоваться командой модуля. В этом случае система

выдаст модуль вектора – т.е. его длину.

2.11 Скалярное и векторное произведение

Скалярным произведением

двух ненулевых векторов

называется число, равное произ-

ведению длин этих векторов на

косинус угла между ними. Ре-

зультатом векторного произведе-

ния, является вектор, а точнее его

координаты. В данном случае

Mathcad выдаёт координаты век-

тора, записанные матрицей. В

данном случае последователь-

ность координат зависит от того, в какой последовательности

они были введены в самих векторах (т.е., если первая строка

отвечает за орт



, то и в векторном произведении первая

строка в получившейся матрице тоже будет отвечать за этот

орт). Необходимо помнить, что во всех векторах, между ко-

торыми будут в дальнейшем производиться действия должны

иметь одинаковую последовательность координат в матрице

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

– т.е. первой строке относиться координата орт



, ко второй

строке относиться координата орт

, к третьей строке отно-

ситься орт

. Необходимые операторы Скалярное произве-

дение и Векторное произведение находятся на панели Мат-

рицы.

2.12 Смешанное произведение векторов

Смешанным произведением трех векторов называется

число





cba 

. Здесь второй и третий вектор перемножаться

векторно, а результат умножается на первый скалярно. Такое

произведение называется ещё векторно-скалярным. Оно

представляет собой некоторое число.

III. Решение систем линейных

алгебраических уравнений

3.1 Общие понятия

Линейная алгебра относится к числу наиболее известных

и хорошо отработанных разделов математики. Векторные и

матричные операторы и функции Mathcad позволяют решать

широкий круг задач линейной алгебры. К числу наиболее

важных относится решение систем линейных алгебраических

уравнений (СЛАУ).

Рассмотрим СЛАУ, в которой число уравнений равно

числу неизвестных. Система, записанная в общем виде:

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru













nnnnnn

bxaxaxa

...

............................................

...

2211

22222121

11212111

Данную систему можно записать в матричной форме:





где















nnn

aaa

...

............

...

21n

22221

11211















...















...

В данном случае необходимо найти вектор столбец

который содержит в себе искомые элементы данной системы

уравнений. Исходя из основ линейной алгебры и аналитиче-

ской геометрии, матрица столбец может быть найдена сле-

дующим образом –





1

где матрица

1

- матрица, обратная к матрице

Для того чтобы решить СЛАУ в Mathcad, необходимо для

заданной системы в рабочем поле Mathcad записать две мат-

рицы – матрицу коэффициентов

и матрицу свободных чле-

нов

, которая является матрицей столбцом. После чего за-

писать выражение вида

BA:X

-1



и вывести значения матри-

цы столбца

. Система выдаст матрицу столбец, которая бу-

дет содержать решения СЛАУ. Однако необходимо помнить,

что если определитель матрицы коэффициентов равен нулю,

то такая СЛАУ называется вырожденной и не имеет единст-

венного решения. В этом случае Mathcad сообщит об ошибке.

Это связано с тем, что в процессе решения СЛАУ необходимо

находить матрицу, обратную к матрице коэффициентов

, а

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

она существует только в том случае, если определитель этой

матрицы отличен от нуля.

Пример – необходимо решить СЛАУ -

















3x5x3x

2x4x

1x3x2x

321

Матрица коэффициентов и матрица свободных членов в

Mathcad будет записана так –















531

401

32-1















После чего для искомого вектора неизвестных записыва-

ем такое выражение –

BA:X

-1



После чего для получения ответа, необходимо просто вы-

вести значение вектора

. Получаем –















X .

Для решения этой же системы можно воспользоваться

функцией lsolve(A,B) – которая также выдаёт матрицу стол-

бец, состоящую из найденных решений (в скобках данной

функции задаются имена матриц через запятую). Для данной

функции

- это матрица коэффициентов для СЛАУ, а

матрица свободных коэффициентов. Результатом также будет

найденный, как и в предыдущем случае, вектор

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Для проверки правильности найденного решения мы мо-

жет просто перемножить матрицу коэффициентов СЛАУ на

найденную матрицу-столбец неизвестных –

XA:N





, получаем -















Замечание:

Если вдруг окажется, что какой-то элемент в матрице ко-

эффициентов СЛАУ или матрице-столбце был введён невер-

но, но нет необходимости заново вводить матрицу коэффици-

ентов или матрицу-столбец свободных членов. Для этого

просто необходимо уже в готовой матрице исправить необхо-

димое число и машина автоматически пересчитает уравнение.

Иногда приходиться иметь дело с системами, в которых

число уравнений меньше, чем число неизвестных. Пример

такой системы:













2x7xx4x9

4x2x2x5x3

6xx3x7x2

4321

В курсе линейной алгебры и аналитической геометрии та-

кие системы решаются по методу Гаусса. Этот метод заклю-

чается в том, что мы вначале записываем расширенную мат-

рицу, после чего приводим её к ступенчатой форме последо-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

вательностью элементарный преобразований, затем от матри-

цы ступенчатой формы обратно переходим к системе уравне-

ний. При этом мы всегда получаем, что некоторые перемен-

ные могут принимать любые значения, определяя все реше-

ния системы, и поэтому система имеет бесконечно много ре-

шений.

В Mathcad данные системы можно решать при помощи

операторов Given и Find. Причём оператор Given определяет

начало решения

системы, а опера-

тор Find выводит

решения этой сис-

темы.

Для решения

этой системы при

помощи операто-

ров Given и Find

необходимо на-

брать с клавиату-

ры ключевое сло-

во «Given», при

этом необходимо после последней буквы оператора «Given»

не нажимать пробел, в противном случае Mathcad воспримет

этот оператор как обычную строку. Далее опустить курсор на

две-три позиции вниз и набрать соответствующее уравнение,

как оно записано в самой системе. При записи этого уравне-

ния не забывать

ставить знак Ум-

ножение, который

находится на пане-

ли Арифметика.

После ввода левой

части уравнения

необходимо поста-

вить вместо тради-

ционного Знак ра-

венства на панели

Арифметика, знак

Булево равенство, который располагается на панели Булево.

В правой части ввести оставшийся свободный член уравне-

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

ния, в нашем случае это «6». Таким же образом ввести все

остальные уравнения системы. При этом желательно вводить

их в столбик, один под другим.

После того, как все необходимые уравнения будут введе-

ны, отступаем несколько строк в низ и записываем с клавиа-

туры оператор «Find», где в скобочках, через запятую указы-

ваем переменные, значения которых нам необходимо вывес-

ти. После того, как все переменные будут введены, необхо-

димо закрыть скобку и вместо традиционного Знак равенст-

ва на панели Арифметика ввести Символический знак ра-

венства, который располагается на панели Вычисления и

имеет форму стрелки. После ввода этого знака Mathcad вы-

даст ответ, который будет решением данной системы. В об-

щем случае данная запись будет похожа на пример, приве-

дённый на рисунке справа.

Если при решении данной задачи предполагается, что ка-

кие-то коэффициенты в данной системе будет меняться, то в

самой системе их необходимо вести как переменные, которые

будет принимать какие-то значения, введённые вверху. Для

системы, состоящей из двух уравнений с тремя неизвестны-

ми, данная запись может принять такой вид, как показано на

рисунке слева. Меняя коэффициенты

dc,b,a,

, Mathcad будет

автоматически пересчитывать значения искомых перемен-

ных.

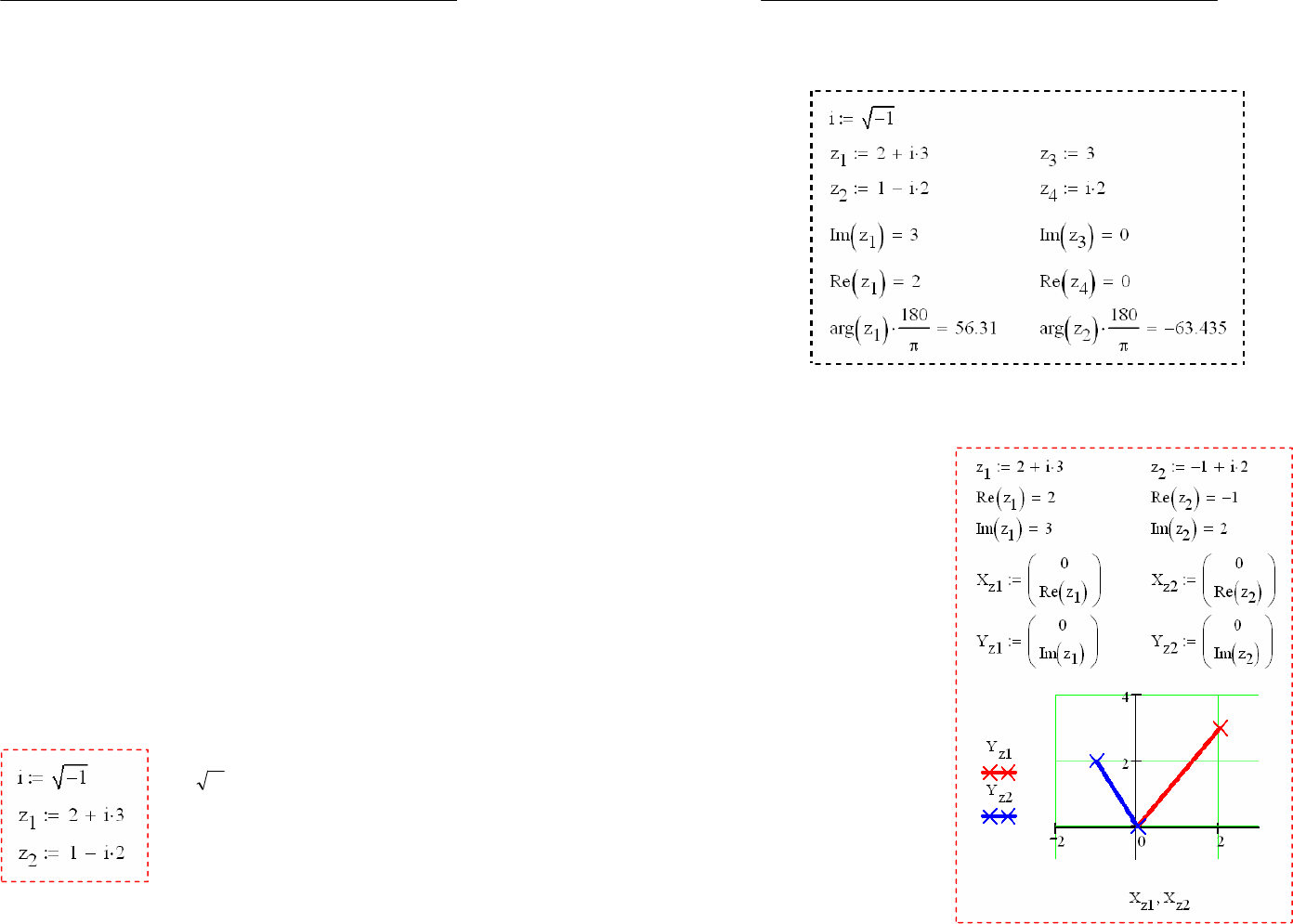
IV. Работа с комплексными числами

4.1 Общие положения

Комплексным числом

называется число вида





где

- действительные числа, а

1-:i

- мнимая единица. Число

назы-

вается действительной частью комплекс-

ного числа

, а

- мнимой частью.

Для того, чтобы начать работать с ком-

плексными числами в Mathcad необходи-

мо в самом начале вычислений задать мнимую единицу. Как

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

правило, в системе Mathcad она обозначается «

» или «

» ,

пользователь сам может выбрать обозначение для нее.

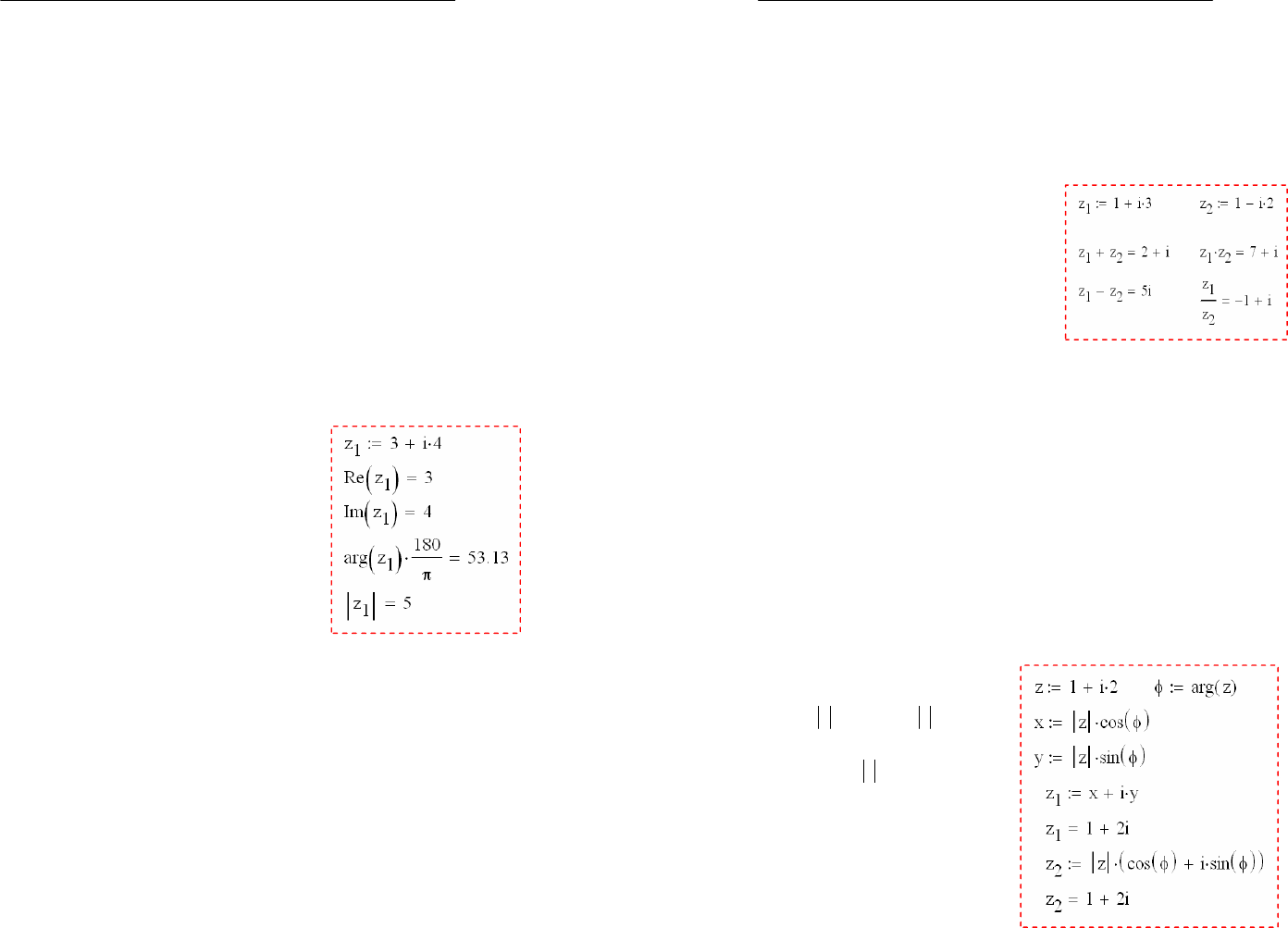
Само комплексное число, состоящее из двух слагаемых,

задаётся действительной частью и комплексной частью, ко-

торая умножается на

мнимую единицу.

Другими словами,

порядок слагаемых

не важен, действи-

тельная и мнимая

часть определяется

не их местом в чис-

ле, а умножением их

на мнимую единицу,

которая и показыва-

ет, что данное сла-

гаемое мнимое, а

отсутствие мнимой

единицы указывает

на то, что это дейст-

вительная часть.

Для упрощения

работы с комплекс-

ными числами в

Mathcad определены

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

некоторые функции:

• arg(z) – вычисление аргумента комплексного числа





;

• Im(z) – выделение мнимой части





;

• Re(z) – выделение действительной части комплексно-

го числа





При изображении комплексного числа на комплексной

плоскости полезно провести аналогию с векторами на плос-

кости. Как известно, для задания вектора на плоскости необ-

ходимо знать проекции этого вектора на оси, которые опре-

деляют эту плоскость. Комплексное число состоит из двух

частей – мнимой части и действительной части, которые од-

новременно являются проекцией вектора (комплексного чис-

ла) на оси комплексной плоскости.

Для того, чтобы изобразить комплексное число на ком-

плексной плоскости в Mathcad’e удобно пользоваться мат-

ричным отображением графиков.

Для этого вводим комплексное чис-

ло, после чего при помощи функций

выделения мнимой и действитель-

ной части комплексного числа вво-

дим матрицы проекций на коорди-

натные оси в последовательности

отображения комплексных чисел.

После этого на графике появятся

отрезки, которые и будут графиче-

ским отображением комплексного числа. Необходимо отме-

тить, что все вектора комплексной плоскости являются ради-

ус-векторами, т.е. координата начала вектора совпадает с на-

чалом системы координат.

Как у любого вектора – у комплексного числа помимо ар-

гумента (т.е. ориентацией вектора в пространстве или други-

ми словами углом) есть ещё и модуль – его длина. В Mathcad

модуль комплексного сила вычисляется также как и модуль

вектора при помощи операции Модуль числа на панели

Арифметика.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

4.2 Сложение, вычитание, умножение и деление

комплексных чисел

Суммой двух комплексных чисел

111

iyxz 

222

iyxz 

называется число









2121213

yyixxzzz 

. Другими сло-

вами, чтобы получить сумму двух комплексных чисел необ-

ходимо сложить их действитель-

ные и мнимые части. Тоже самое

и при вычитании одного ком-

плексного числа из другого:









2121213

yyixxzzz 

При перемножении ком-

плексных чисел необходимо

пользоваться правилом раскры-

тия скобок, при этом надо помнить, что

1-:

i

Арифметические операции над комплексными числами в

среде Mathcad осуществляются точно так же, как и с обыч-

ными числами и выражениями.

4.3 Тригонометрическая и показательная

форма записи комплексного числа

Помимо алгебраической («





» - эта форма записи

комплексного числа называется алгебраической формой запи-

си комплексного числа) существует ещё тригонометрическая

и показательная форма записи комплексного числа.

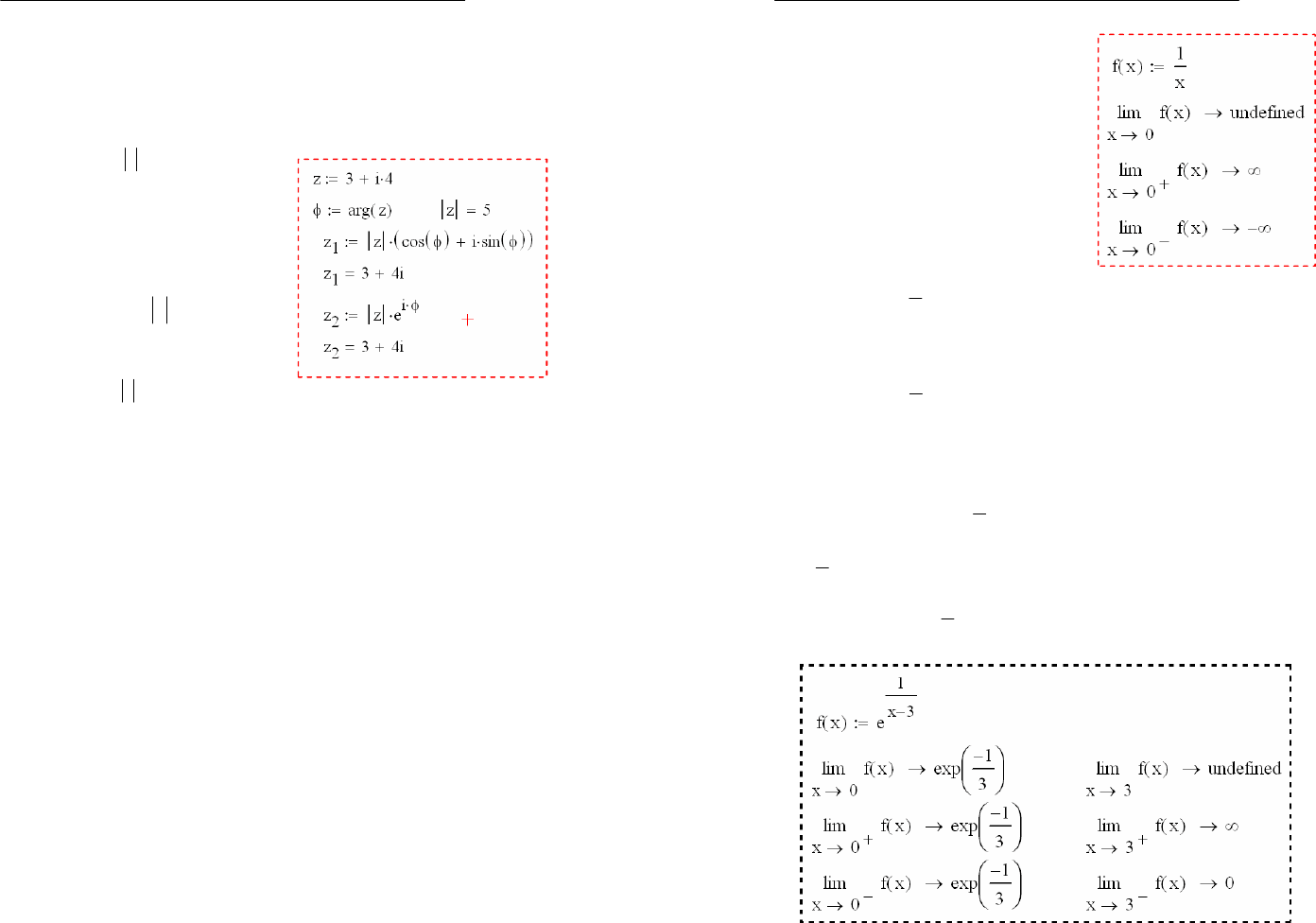
Используя выражения

для модуля и аргумента:

,cos



zх 

,sin



zу 

можно записать

)sin(cos



izz 

Такая запись называется

тригонометрической фор-

мой комплексного числа.

Показательные и триго-

нометрические функции в

области комплексных чисел

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

связаны между собой формулой:





sincos iе

 ,

которая называется формулой Эйлера.

Пусть комплексное число z в тригонометрической форме

имеет вид

)sin(cos



izz 

На основании формулы Эй-

лера выражение в скобках мож-

но заменить показательным вы-

ражением. В результате полу-

чим



ezz 

Эта запись называется по-

казательной формой комплекс-

ного числа,

z

модуль числа;

φ – аргумент числа.

V. Вычисление пределов функций

Общие положения

Пределом функции

f(x)

называют то её значение

, к ко-

торому функция неограниченно приближается в точке



(предел в точке) или слева или справа от неё.

• предел в точке «

» -

bf(x)lim 

ax

;

• предел слева от точки «

» -

bf(x)lim 

ax

;

• предел справа от точки «

» -

bf(x)lim 

ax

При этом подразумевается, что сама функция

f(x)

опре-

делена на некотором промежутке, включающем точку



и во всех точках, близких к ней слева и справа. В последнем

случае предел вычисляется для

k-ax



или

kax





, при

стремящимся к нулю. Пределом может быть число, матема-

тическое выражение и положительная или отрицательная

бесконечность.

автор: Денисов-Винский Н.Д.

E-mail: denisov.vinskiy@yandex.ru

Как правило, предел необхо-

димо вычислять в точках, где

функция существовать не может,

однако необходимо знать поведе-

ние этой функции вблизи этой

точки. При этом необходимо пом-

нить, что, как правило, пределы

вблизи точки, в которой функция

не существует, справа и слева -

различны.

Примеров может служить

функция

f(x) 

. В данном случае на область определения

функции накладывается условие -



. В точке



функ-

ция не существует. Из этого следует, что численное значение

функции

f(x) 

в точке



мы найти не можем. В этом

случае вычислять предел в точке будет не совсем правильно,

т.к. значение функции будет зависеть от того, с какой сторо-

ны от этой точке мы будем устремляться к ней. При

-0x



мы получаем -

















lim

, в тоже время при





















lim

. Таким образом, точка



есть точка разрыва

для функции

f(x) 