Денискина Е.А., Коломиец П.Э. (сост) Статистический анализ данных
Подождите немного. Документ загружается.

41
0,95
1
2
(98) (98) 1,661tt
α
−
==, 661,1)98()98(
05,0
2
−=
=
tt
α
,
4,9961
1,661 99 1,661
2,2657
m
−
−< <
Выражая из неравенства неизвестный параметр m, получим доверительный
интервал для математического ожидания для уровня значимости
1,0=
α
:
4,6178 5,3743m
<
< .
Таким образом, неизвестное математическое ожидание
()
4,6178 ; 5,3743m ∈ с вероятностью 9,0
=
p .
Аналогично найдем доверительные интервалы для математического
ожидания для уровней значимости
0,05
α
=
и 01,0
=
α
.
0,05
α
= : 025,0
2
=
α
, 975,0
2
1 =−
α
, 981991
=
−=−
=
n
k
,
0,975
1
2
(98) (98) 1,984tt
α
−
==,
0,025
2
(98) (98) 1,984tt
α
=
=− ,
4,9961
1,984 99 1,984
2,2657
m
−
−< <.
Выражая из неравенства неизвестный параметр m, получим доверительный
интервал для математического ожидания для уровня значимости
5,0=
α
:
4,5442 5,4479m
<
< .
Таким образом, неизвестное математическое ожидание
()
4,5442 ; 5,4479m ∈ с вероятностью 95,0
=
p .
01,0=
α
: 005,0
2
=
α
, 995,0
2
1 =−
α
,
981991
=
−=−
=
n
k
,
0,995
1
2
(98) (98) 2,627tt
α
−
==,
0,005
2
(98) (98) 2,627tt
α
=
=− ,
4,9961
2,627 99 2,627
2,2657
m
−
−< <.
42
Выражая из неравенства неизвестный параметр
m, получим доверительный
интервал для математического ожидания для уровня значимости
01,0=
α
:
4,3978 5,5948m
<
< .
Таким образом, неизвестное математическое ожидание
()
4,3978 ; 5,5948m ∈ с вероятностью 99,0
=
p .
1.9.2. Определим теперь доверительный интервал для неизвестной
дисперсии
2
σ
нормально распределенной случайной величины X с
неизвестным математическим ожиданием и заданным уровнем значимости
α
.
В этом случае рассматривается статистика
)1(
2
2
0
−= n
S
B
σ
, имеющая
распределение
2
χ
с
1−= n
k
степенями свободы, где n – объем выборки.
Будем искать доверительную область в виде:
∫
−===<<
2
1
1)()(
2
2
1
θ
θ
αθχθ
pdxxfP
kp
.
Рис. 12
Квантили распределения
2
χ
1
p
2
2
α
χ
2
2
1
α
χ
−
)(
x
f
k
0
2/
2/
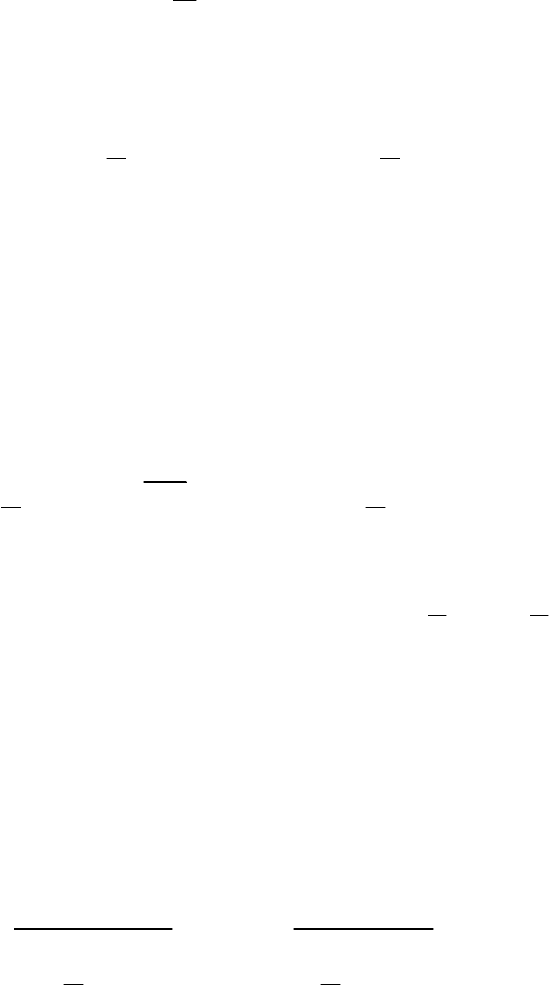
43
Как и в предыдущем случае, будем считать площади под «хвостами»
кривой распределения равными по
2
α
каждая (рис. 12).
Тогда границы интервала совпадут с квантилями:
(
)
2
1
2
1n
α
θχ
=−,
(
)
2
2
1
2
1n
α
θχ
−
=
− .
В таблице П 5 Приложения приведены значения
)(
2
k
p
χ
в зависимости
от доверительной вероятности
p и числа степеней свободы k . Можно также
использовать функцию ХИ2ОБР пакета прикладных программ EXCEL.
Таким образом, получаем
2
22
0
2
1
22
(1) (1) (1)
S
nn n
αα
χχ
σ
−
−< − < −.
Подставив в полученное неравенство значения
2
2
α
χ
,
2
2
1
α
χ
−
,
2
0
S
, n и
разрешив это неравенство относительно
2
σ
, получим доверительный интервал
для неизвестной дисперсии
2
σ
нормально распределенной случайной
величины
X с неизвестным математическим ожиданием и заданным уровнем
значимости
α
:
22
2
00
22
1
22
(1) (1)
(1) (1)
nS nS
nn
αα
σ
χχ
−
−⋅ −⋅
<<
−
−
.
Следует отметить, что если математическое ожидание генеральной
совокупности известно, то доверительный интервал для дисперсии будет иметь
другой вид.
Длина доверительного интервала характеризует точность оценивания и
зависит от объема выборки
n и доверительной вероятности
α
−= 1p . Чем
меньше длина доверительного интервала, тем надежнее оценка. При
увеличении объема выборки длина доверительного интервала уменьшается.

44
П Р И М Е Р 7
(пункт 9 части 1 Задания):
Требуется построить доверительный интервал для неизвестной дисперсии
нормально распределенной генеральной совокупности с параметрами
mx
=
и
0
S=
σ
для уровней значимости 1,0
=
α
, 05,0
=
α
и 01,0
=
α
.
Для построения доверительного интервала для неизвестной дисперсии
2
σ
нормально распределенной генеральной совокупности используется
статистика
)1(
2
2
0
−⋅= n
S
B
σ
, имеющая распределение
2
χ
с
1
−
=
n
k
степенями свободы:
2
2
1
2
2
0
2
2
)1(
αα
χ
σ
χ
−
<−⋅< n
S
.
Вычислим этот интервал для различных уровней значимости.
1,0=
α
: 05,0
2
=
α
, 95,0
2
1 =−
α
, 981991
=
−=
−
=
n
k
.
Так как в таблице П 5 Приложения нет числа степеней свободы
98=
k
, то для
вычисления
)(
2
k
p
χ
можно воспользоваться одним из способов:
1. Известно, что при
30≥
k
2
)12(
)(
2
2
−+
≈
kC
k
p
p
χ
, где
p
C –
квантиль нормального распределения (таблица П 3 Приложения).
По этой формуле получим:
2
0,05
22
0,05
2
( 2 98 1)
(98) (98) 75,882
2
C
α
χχ
+⋅−
=≈ =
,
2
0,95
22
0,95
1
2
( 2 98 1)
(98) (98) 121,824
2
С
α
χχ
−
+⋅−
=≈ =
.
2. Статистическая функция ХИ2ОБР пакета EXCEL дает следующие
значения квантилей распределения хи- квадрат:
(
)
2
0,05
98 76,164
χ
= ,
(
)
2
0,95
98 122,108
χ
= .

45
Следует иметь в виду, что в функции ХИ2ОБР вычисляются
«антиквантили»
(
)
pBP
p
=>
2
χ
. Чтобы получить значение квантили
()
2
0,05
98
χ
, нужно ввести обратную вероятность 95,0
=
p .
В дальнейших расчетах используются значения квантилей, вычисленные
в EXCEL:
108,122)199(
1332,5
164,76
2
<−⋅<
σ
Выражая из неравенства неизвестный параметр
2
σ
, получим
доверительный интервал для дисперсии для уровня значимости
1,0=
α
:
6049,61197,4
2
<<
σ
.
Таким образом, неизвестная дисперсия
2
( 4,1197 ; 6,6049 )
σ
∈ с
вероятностью
9,0=p .
Аналогично найдем доверительные интервалы для дисперсии для
уровней значимости
0,05
α
= и 01,0
=
α
.
0,05
α
= : 025,0
2
=
α
, 975,0
2
1 =−
α
, 981991
=
−=−
=
n
k
,
22
0,025
2
(98) (98) 72,501
α
χχ
==,
22
0,975
1
2
(98) (98) 127, 282
α
χχ
−
==,
282,127)199(
1332,5
501,72
2
<−⋅<
σ
.
Выражая из неравенства неизвестный параметр
2
σ
, получим
доверительный интервал для дисперсии для уровня значимости
05,0=
α
:
9386,69523,3
2
<<
σ
.
Таким образом, неизвестная дисперсия
2
( 3,9523 ; 6,9386 )
σ
∈ с
вероятностью
95,0=p .
01,0=
α
:
005,0
2
=
α
,
995,0
2
1 =−
α
, 981991
=
−=
−
=
n
k
,

46
22
0,005
2
(98) (98) 65,693
α
χχ
==,
22
0,995
1
2
(98) (98) 137,803
α
χχ
−
==,
803,137)199(
1332,5
693,65
2
<−⋅<
σ
.
Выражая из неравенства неизвестный параметр
2
σ
, получим
доверительный интервал для дисперсии для уровня значимости
01,0=
α
:
6576,76505,3
2
<<
σ
.
Таким образом, неизвестная дисперсия
2
( 3,6505 ; 7,6576 )
σ
∈ с
вероятностью
99,0=p
.
Заметим, что полученные ранее выборочное среднее
9961,4=
x
и
выборочная дисперсия
1332,5
2
0
=S
попадают во все найденные
доверительные интервалы соответственно, причем, чем меньше уровень
значимости
α
, то есть больше вероятность
α
−
=
1p , тем больше длина
соответствующего доверительного интервала.
2. СТАТИСТИЧЕСКИЙ АНАЛИЗ ДВУМЕРНЫХ
ДАННЫХ
В практических применениях теории вероятностей очень часто
приходится сталкиваться с задачами, в которых результат опыта описывается
не одной случайной величиной, а двумя или более случайными величинами.
Изучение каждой из этих случайных величин отдельно от другой может
привести к недопустимому упрощению вероятностной модели явления. В
данном разделе рассматриваются такие методы статистического анализа
двумерных данных, как корреляционный и регрессионный анализ.
47
2.1. ФУНКЦИОНАЛЬНАЯ, СТАТИСТИЧЕСКАЯ
И КОРРЕЛЯЦИОННАЯ ЗАВИСИМОСТИ
Рассмотрим зависимость случайной величины Y от одной величины X
(случайной или детерминированной).
Если каждому возможному значению
X соответствует единственное
возможное значение
Y , то Y называют функцией аргумента X . Строгая
функциональная зависимость между двумя случайными величинами
реализуется редко, так как обе величины могут быть подвержены воздействию
случайных факторов.
Статистической называется зависимость, при которой изменение
одной из величин влечет за собой изменение закона распределения другой.
Если статистическая зависимость проявляется в том, что при изменении
одной величины изменяется среднее значение (математическое
ожидание)
другой, то зависимость называется корреляционной.
Между функциональной и корреляционной зависимостями случайных
величин существует связь.
1. Если случайные величины
X и Y функционально зависимы, то они
коррелированы. Обратное утверждение, в общем, не верно.
2. Если
X и Y независимы, то они некоррелированы. Обратное
утверждение, в общем, не верно.
Таким образом, корреляционная зависимость занимает промежуточное
значение между функциональной зависимостью и независимостью. Поэтому
корреляционную зависимость считают «слабой» зависимостью между
случайными величинами.
2.2. ЛИНЕЙНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Пусть имеется n наблюдений случайного вектора
()
YX , . При этом
{}
n
xxxX ,,,
21
K=
и
{}
n
yyyY ,,,
21
K=
.
По данным наблюдениям можно вычислить следующие статистики:
48
∑
=
⋅=
n
i
i
x
n
x
1
1
– выборочное среднее случайной величины X ;
∑
=
⋅=
n
i
i
y
n
y
1
1
– выборочное среднее случайной величины Y ;
∑
=
⋅⋅=⋅
n
i
ii
yx
n
yx
1
1
– выборочное среднее произведений случайных величин;
()
∑
=
−⋅==
n
i
iXX
xx
n
D
1
2
2
1
~
~
σ
– выборочная дисперсия случайной величины X ;
()
∑
=
−⋅==
n
i
iYY
yy
n
D
1
2
2
1
~
~
σ
– выборочная дисперсия случайной величины Y ;
yxyxyyxx
n
K
n
i
iiXY
⋅−⋅=−−⋅=
∑
=1
))((
1
~
– выборочный корреляционный
момент.
Все эти статистики являются оценками соответствующих параметров
генеральной совокупности, вычисленными по данной выборке наблюдений.
Выборочным коэффициентом корреляции
XY
r
~
называется отношение
выборочного корреляционного момента
X
Y
K
~
к произведению выборочных
среднеквадратических отклонений величин
X и Y :
Y
X
Y
X
XY
XY
yxyx
K
r
σσσσ
~~~~
~
~
⋅
⋅−⋅
=
⋅
=
.
Выборочный коэффициент корреляции можно вычислить также с
помощью функции КОРРЕЛ пакета EXCEL.
Если выборочный коэффициент корреляции равен нулю, то случайные
величины называются некоррелированными. Из независимости случайных
величин следует некоррелированность, то есть для независимых случайных
величин коэффициент корреляции равен нулю. Обратное утверждение в общем

49
случае неверно, из коррелированности случайных величин не всегда следует их
независимость.
Выборочный коэффициент корреляции характеризует линейную
зависимость. Линейная вероятностная зависимость случайных величин
заключается в том, что при возрастании одной случайной величины другая
имеет тенденцию возрастать (или убывать) по линейному закону. Если
случайные величины
X и Y связаны точной линейной зависимостью:
baX
Y
+
=
,
то
1
~
±=
XY
r , причем знак «плюс» или «минус» берется в зависимости от того,
положителен или отрицателен коэффициент
a . В общем случае, когда
величины
X и Y связаны произвольной вероятностной зависимостью,
выборочный коэффициент корреляции может иметь значения в пределах:
11
X
Y
r
−
≤≤
%
.
В случае
0
~
>
XY
r говорят о положительной корреляции величин X и Y , в
случае
0
~
<
XY
r – об отрицательной корреляции. Положительная корреляция
между случайными величинами означает, что при возрастании одной из них
другая имеет тенденцию в среднем возрастать; отрицательная корреляция
означает, что при возрастании одной из случайных величин другая имеет
тенденцию в среднем убывать.
По величине коэффициента корреляции можно судить о тесноте связи
между случайными величинами
X и Y : если его значение по модулю близко к
единице, то связь достаточно тесная; если
0
XY
r
≈
%
, то связь между случайными
величинами слабая.
П Р И М Е Р 8
(пункт 1 части 2 Задания):
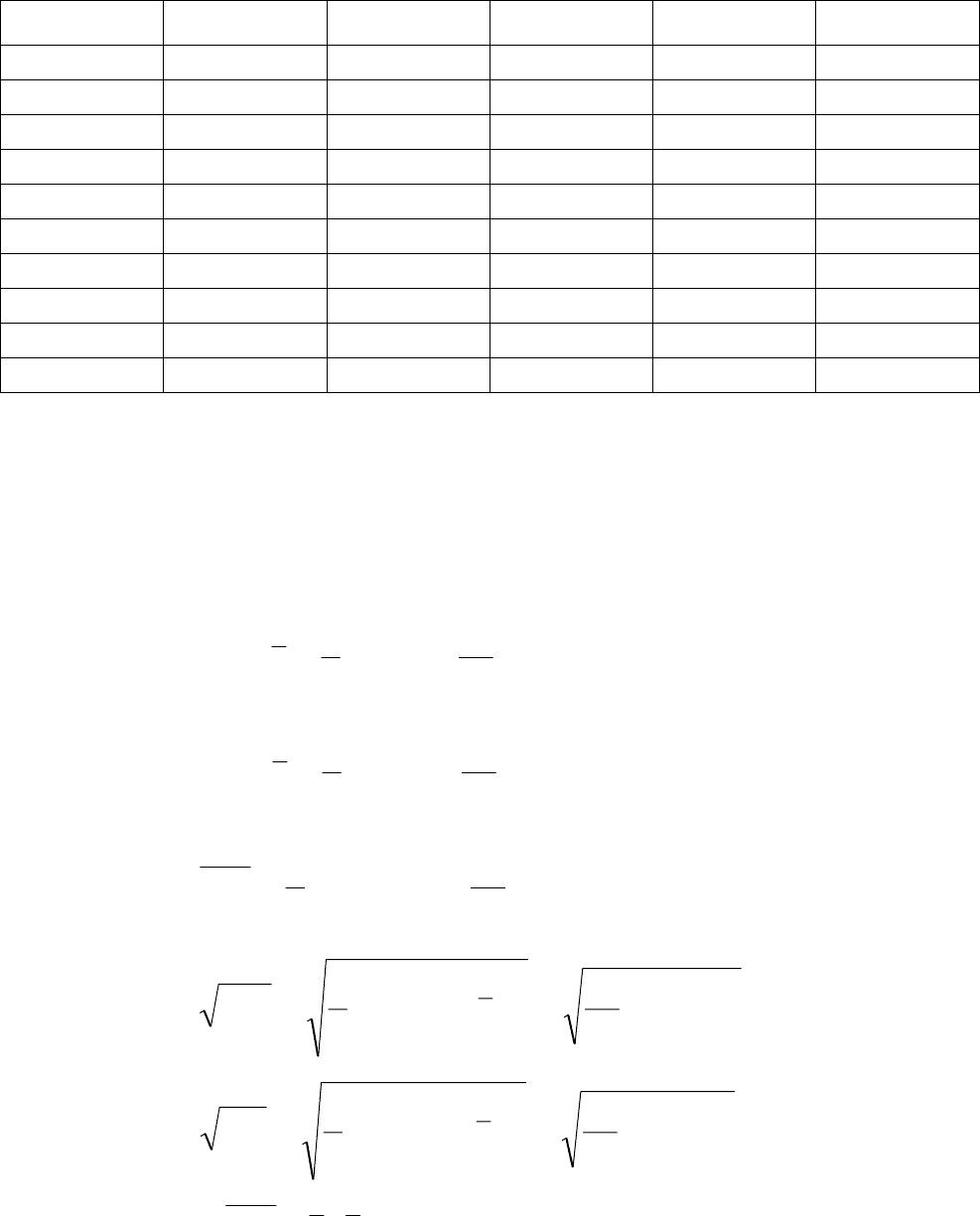
В таблице 12 представлены результаты испытаний двух случайных
величин
X и Y .
50
Таблица 12
i
i
x
i
y
i
i
x
i
y
1
4,08 2,14
11
4,31 6,29
2
6,91 3,00
12
2,34 5,52
3
7,42 1,73
13
3,82 3,11
4
3,58 4,24
14
3,98 5,70
5
5,16 3,27
15
3,24 2,60
6
5,19 2,83
16
2,88 5,13
7
4,10 4,22
17
6,19 1,44
8
5,37 4,40
18
5,86 2,20
9
5,02 2,19
19
2,67 3,58
10
6,19 3,20
20
4,36 3,90
Требуется определить выборочный коэффициент корреляции и
проанализировать результаты.
Вычислим необходимые для нахождения выборочного коэффициента
корреляции оценки параметров распределения генеральной совокупности:
6335,467,92
20
11
1
=⋅=⋅=
∑
=
n
i
i
x
n
x ,
5345,369,70
20
11
1
=⋅=⋅=
∑
=
n
i
i
y
n
y
,
3465,159292,306
20
11
1
=⋅=⋅⋅=⋅
∑
=
n
i
ii
yx
n
yx ,
3725,16767,37
20
1
)(
1
~
~
1
2
=⋅=−⋅==
∑
=
n
i
iXX
xx
n
D
σ
,
3381,18161,35
20
1
)(
1
~
~
1
2
=⋅=−⋅==
∑
=
n
i
iYY
yy
n
D
σ
,
0306,15345,36335,43465,15
~
−=⋅−=⋅−⋅= yxyxK
X
Y
.
Найдем теперь выборочный коэффициент корреляции:
