Давнис В.В., Щепина И.Н. и др. Элементы экономико-математического моделирования
Подождите немного. Документ загружается.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра Информационных Технологий
и математических методов в экономике
Лабораторный практикум
по курсу
Элементы экономико-математического
моделирования
Для студентов 2-4 курсов дневного и вечернего отделений
экономического факультета
Составители: В .В . Давнис
И . Н . Щепина
С.И. Мокшина
О .С. Воищева
С.С. Щекунских
Воронеж 2001

Элементы ЭММ
2
Введение.
Круг вопросов , рассматриваемых в предлагаемом
лабораторном практикуме, включает в себя раскрытие понятий и
методов математического моделирования социально –
экономических систем и процессов . Рассматриваются балансовые
модели в статической постановке, однофакторные и
многофакторные модели регрессии, модель частичного рыночного
равновесия – паутинообразная модель. Кроме того, в
лабораторный практикум включены такие прикладные модели , как
модель формирования производственной функции, модель фирмы
и модель потребления.
Подробно, на примере конкретного задания по каждой теме,
описана последовательность проведения расчетов по
формированию экономико – математической модели . Для
самостоятельной работы студентов предусмотрены лабораторные
задания.
Цель лабораторного практикума – закрепление знаний по
теории и практическому использованию математических моделей
в сложных экономических расчетах и выработка навыков
проведения расчетов с использованием электронных таблиц
EXCEL в среде WINDOWS.
1. Основные операции матричной алгебры в EXCEL
Приведенные ниже упражнения предлагаются студентам для
самостоятельного выполнения с целью повторения и закрепления
навыков работы с табличным процессором EXCEL при
выполнении основных операций матрично-векторной алгебры .
1. Для матрицы А=
−− 325
436
752
найти ее определитель A ,
обратную матрицу
1
A
−
, произведение
1
A
*
A
−
и
A
*
A
1−
.

Элементы ЭММ
3
2. Для матриц С=
213
210
121
и D=
−
−
121
011
132
найти
C
,
D
,
DCCD
и проверить справедливость равенства:
.)DC(C*DD*C)CD(
111111
−
−
−
−
−
−
===
3. Вычислить D=ABC-3E, где А=
−
401
210
321
, В=
3
2
1
,
С=
[
]
502
.
4. Вычислить D=
2'
C)AB( − , где А=
501
243
, В=
50
31
02
,
С=
40
30
.
5. Вычислить матрицу В=
,A)A(*11
''1
+
−
где
А=
−
−−
−
132
111
142
.
6. Найти
,EC*BA*AX
1
++=
−
если
−
−
=
111
012
111
A
,
−
−
=
211
543
150
B
,
−
−=
357
121
123
C
7. Предприятие производит продукцию трех видов и использует
сырье двух типов . Нормы затрат сырья на единицу продукции
каждого вида заданы матрицей А=
431
312
. Стоимость
единицы сырья каждого типа задана матрицей В=
[
]
1510 .
Элементы ЭММ
4
Каковы общие затраты предприятия на производство 100
ед.продукции 1-го вида, 200 ед. продукции 2-го вида и 150 ед .
продукции 3-го вида?
8 .Обувная фабрика специализируется по выпуску изделий трех
видов : сапог , кроссовок и ботинок ; при этом используется сырье
трех типов : S1, S2, S3. Нормы расхода каждого из них на одну
пару обуви и объем расхода сырья на 1 день заданы таблицей:
Нормы расхода сырья на одну
пару , усл.ед.
Вид сырья
Сапоги Кроссовки Ботинки
Расход сырья
на 1 день,
усл.ед.
S1 5 3 4 2700
S2 2 1 1 800
S3 3 2 2 1600
Найти ежедневный объем выпуска каждого вида обуви, решив
систему уравнений методом обратной матрицы.
2. Экономико - математическая модель материального баланса
производства и распределения продукции
2.1. Принципиальная схема межотраслевого баланса и основные
балансовые соотношения.
Предположим, что экономическая система состоит из n
взаимосвязанных отраслей (предприятий, экономических
объектов ). Каждая отрасль выступает в роли поставщика
производимой ею продукции и в роли потребителя продукции
других отраслей системы.
Введем обозначения:
i
- порядковый номер отрасли , производящей продукцию,
(
i
=1,2,… ,n);
j
- порядковый номер отрасли , потребляющей продукцию,
(
=
j
1,2,… ,n);
i
X
- валовой продукт i-ой отрасли
i
Y - конечный продукт j-ой отрасли
ij
x - затраты продукции i-ой отрасли на производство продукции

Элементы ЭММ
5
j-ой отрасли ;
j
V
- условно-чистая продукция j-ой отрасли ;
Вся информация об экономической системе представлена в
таблице:
Отрасли
1 2 …
j …
n Итого Кон .
прод.
Вал.
прод.
1
11
x
12
x
j1
x
n
1
x
∑
j
j1
x
1
Y
1
X
2
21
x
22
x
j2
x
n
2
x
∑
j
j2
x
2
Y
2
X
…
i
1
i
x
2
i
x
ij
x
in
x
∑
j
ij
x
j
Y
j
X
…
n
1
n
x
2
n
x
nj
x
nn
x
∑
j
nj
x
n
Y
n
X
Итого
∑
i
1i
x
∑
i
2i
x
∑
i
ij
x
∑
i
in
x
∑
∑
ij
ij
x
∑
i
i
Y
∑
i
i
X
Услов .-
чистая
прод.
1
V
2
V
j
V
n
V
∑
j
j
V
Валовой
прод.
1
X
2
X
j
X
j
X
∑
j
j
X
Основные балансовые соотношения:
1.
,xYX
n
1j
ijii
∑
=
+=
n
,...,
2
,
1
i
=
(1)
- баланс между производством и потреблением .
2.
,xVX
n
1
i
ijjj
∑
=
+=
n
,...,
2
,
1
j
=
(2)
- стоимостная структура продукции j-ой отрасли .
3.
∑∑
==
=
n
1j
j
n
1i
i
VY
(3)
- равенство суммарного конечного продукта и суммарной условно-
чистой продукции.

Элементы ЭММ
6
4.
∑∑
==
n
1i
n
1j
ij
x
- промежуточный продукт экономической системы.
2.2. Построение математической модели
Введем в рассмотрение коэффициенты прямых затрат или
технологические коэффициенты , рассчитанные по формуле:
,jijij
X/xa
=
n
,...,
2
,
1
j
,
i
=
(4)
Коэффициенты
ij
a
показывают, сколько единиц продукции
i-ой отрасли непосредственно затрачивается в качестве средств
производства на выпуск единицы продукции j-ой отрасли .
Использование коэффициентов прямых затрат позволяет
представить запись баланса (1) в виде:
,XaYX
n
1j
jijii
∑
=
+=
n,...,2,1i
=
(5)
Если ввести следующие обозначения:
=
nn2n1n
n22221
n11211
a...aa
............
a...aa
a...aa
A
,
=
n
2
1
X
...
X
X
X
,
=
n
2
1
Y
...
Y
Y
Y ,
то систему (5) можно записать в матрично-векторной форме:
X
Y
AX
=
+
. (6)
Система уравнений межотраслевого баланса является
отражением реальных экономических процессов , в которых
содержательный смысл могут иметь лишь неотрицательные
значения валовых выпусков . Таким образом, вектор валовой
продукции состоит из неотрицательных компонентов и называется
неотрицательным:
0
X
≥
. Встает вопрос, при каких условиях
экономическая система способна обеспечить положительный
конечный выпуск по всем отраслям . Ответ на этот вопрос связан с
понятием продуктивности матрицы коэффициентов прямых
материальных затрат. Достаточным признаком продуктивности
матрицы А является ограничение на величину ее нормы, т .е. на
величину наибольшей из сумм элементов матрицы А в каждом
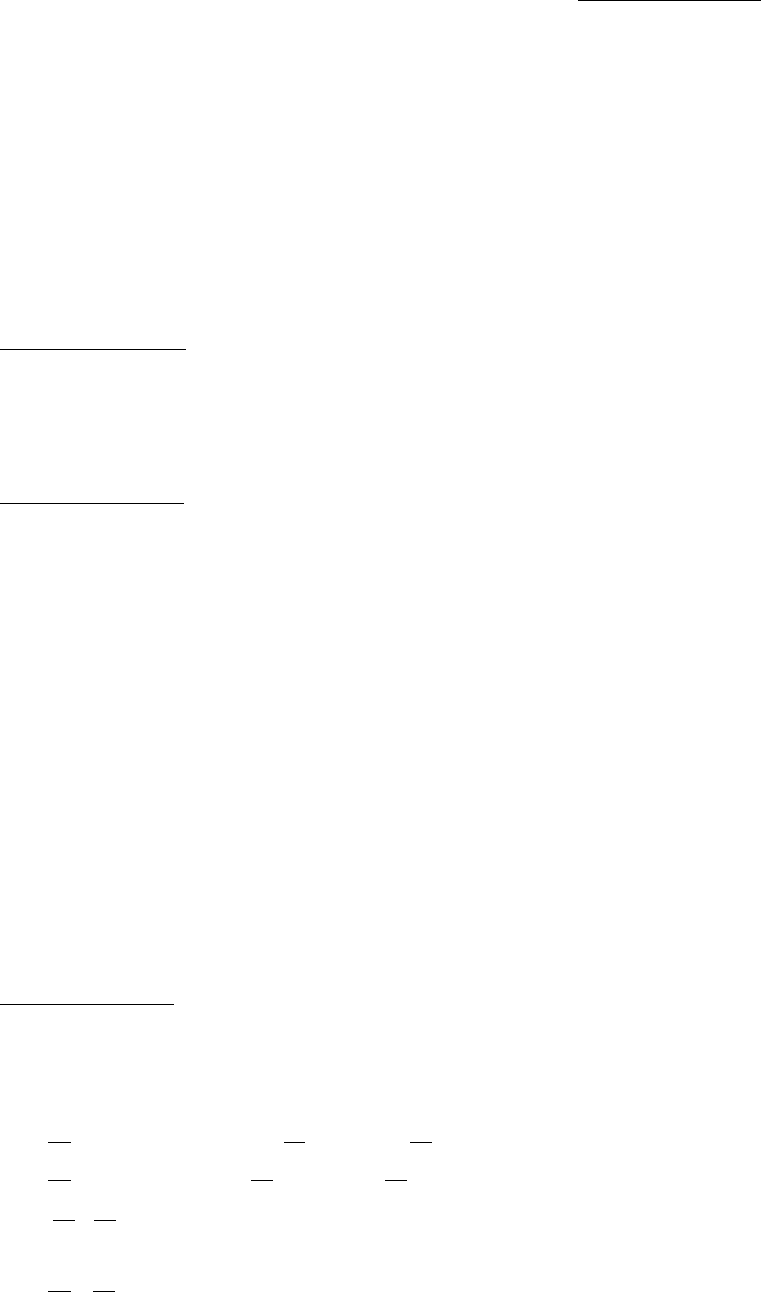
Элементы ЭММ
7
столбце. Если норма матрицы А строго меньше единицы, то эта
матрица продуктивна.
Условие о том , что
ij
a
постоянны в некотором промежутке
времени, охватывающем как отчетный, так и планируемый перио-
ды , позволяет решать задачу , заключающуюся в том, чтобы на
базе данных об исполнении баланса за предшествующий
(отчетный) период определить данные на планируемый период.
Эта задача может быть поставлена в трех вариантах.
Первый вариант: по заданным валовым уровням производства
всех отраслей (задан вектор
X
) определить объемы выпуска
конечной продукции (вектор
Y
). В этом случае систему (6)
удобно записать в виде:
.
X
*
A
X
Y
−
=
(7)
Второй вариант: по заданным уровням конечной продукции
отраслей (вектор
)Y
определить объемы валовой продукции
(вектор
)
X
. В этом случае система (6) переписывается в виде:
,Y*)AE(X
1
−
−= (8)
где
E
- единичная матрица размерности n;
1
)AE(
−
−
- обратная матрица к матрице
A
E
−
.
Элементы этой матрицы есть коэффициенты полных
материальных затрат, показывающие, сколько всего нужно
произвести продукции i-ой отрасли , чтобы получить единицу
конечной продукции j-ой отрасли . Исходя из того, что кроме
прямых затрат существуют косвенные затраты той или иной
продукции на предшествующих стадиях производства, имеет
место следующее определение: коэффициентом полных
материальных затрат называется сумма прямых и косвенных
затрат продукции.
Третий вариант: по отдельным отраслям задаются уровни валовой
продукции, по другим - уровни конечного продукта (в сумме
число заданных величин равно n). Требуется определить значения
остальных n переменных. В этом случае расчет неизвестных
осуществляется по комбинированной схеме:
)X*AY(*)AE(X
2
12
1
1
11
1
+−=
−
(9)
,X*AX*)AE(Y
1
21
2
22
2
−
−
=
(10)
где
2
1
X,Y
- векторы заданных уровней конечного и валового
продуктов ;
2
1
Y,X
- векторы искомых уровней валового и конечного
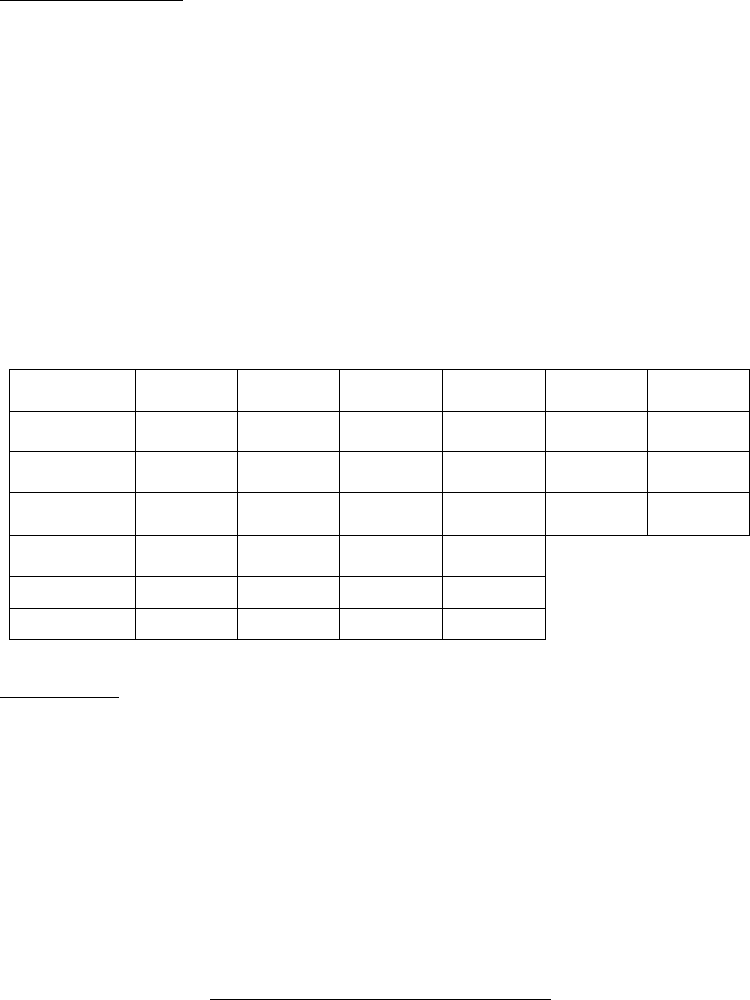
Элементы ЭММ
8
продуктов ;
ik
A
,
2
,
1
k
,
i
=
- блоки разбиения матрицы
коэффициентов прямых затрат А.
2.3. Пример и порядок выполнения лабораторного задания
Располагая следующими данными об экономической системе,
состоящей из трех экономических объектов :
1
P-
промышленность,
2
P
- сельское хозяйство,
3
P
- транспорт :
Отрасли
1
P
2
P
3
P
∑
Y
X
1
P
20 50 200 300
2
P
10 0 40 500
3
P
0 240
∑
310
V
390
X
Требуется:
1. Завершить составление баланса .
2. Рассчитать матрицу коэффициентов прямых затрат, полных
затрат, косвенных затрат.
3. Рассчитать валовые выпуски 1-ой и 2-ой отраслей и конечный
продукт 3-ей отрасли на планируемый период при условии
увеличения конечного продукта первых двух отраслей на 3%,
оставив без изменения объем валового продукта 3-ей отрасли .
4. Рассчитать новую производственную программу каждой
отрасли .
Порядок выполнения задания.
1. Составление баланса .
1.1. Используя баланс между производством и потреблением
продукции отрасли
1
P, найдем ,x
3
1j
j1
∑
=
а затем :x
13
100200300YXx
11
3
1j
j1
=−=−=
∑
=

Элементы ЭММ
9
30)5020(100)xx(xx
1211
3
1j
j113
=+−=+−=
∑
=
1.2. Используя баланс между производством и потреблением
продукции отрасли
,P
2
найдем
,Y
2
предварительно
подсчитав :x
3
1j
j2
∑
=
45050500xXY
5040010x
3
1j
j222
3
1j
j2
=−=−=
=++=
∑
∑
=
=
1.3. Используя соотношение между элементами столбца
∑
,
найдем
:x
n
1j
j3
∑
=
16050100310xxxx
j
j2
j
j1
ij
ij
3
1j
j3
=−−=−−=
∑∑∑∑∑
=
1.4. Используя баланс между производством и потреблением
продукции отрасли ,P
3
найдем :X
3
400160240xYX
j
j333
=
+
=
+
=
∑
1.5. Вычислим суммарные затраты всех трех отраслей на
производство продукции первой отрасли
301020x
3
1j
j1
=+=
∑
=
1.6. Используя стоимостную структуру продукции отрасли
,P
1
найдем ее условно чистую продукцию
:V
1
27030300xXV
3
1j
j111
=−=−=
∑
=
1.7. Используя соотношение (3), получим условно чистую
продукцию отрасли :P
3
230
390270240450200VVYV
21
3
1j
j3
=−−++=−−=
∑
=

Элементы ЭММ
10
1.8. Определим суммарные затраты на производство
продукции отраслей
2
P
и
:P
3
110390500VXx
22
3
1
i
2i
=−=−=
∑
=
170230400VXx
33
3
1
i
3i
=−=−=
∑
=
1.9. Определим затраты продукции отрасли
3
P на
производство продукции
2
P
и на собственные
производственные нужды :
1004030170xxxx
60050110xxxx
2313
3
1i
3i33
2212
3
1i
2i32
=−−=−−=
=−−=−−=
∑
∑
=
=
Окончательно получаем :
Отрасли
1
P
2
P
3
P
∑
Y
X
1
P
20 50 30 100 200 300
2
P
10 0 40 50 450 500
3
P
0 60 100 160 240 400
∑
30 110 170 310
V
270 390 230
X
300 500 400
2. Расчет матрицы коэффициентов прямых затрат, полных затрат и
косвенных затрат.
2.1. Элементы матрицы коэффициентов прямых затрат
рассчитаем по формуле (4), получим:
=
25.012.00
1.00033.0
075.01.0066.0
A
2.2. Проверка условия
∑
i
ij
a
< 1, j=1,2, … ,n , гарантирующего
существование решения:
