Даньшин Ю.В., Поспелов А.И. Кинематическое исследование зубчатых механизмов

МПС РФ

Дальневосточный государственный

университет путей сообщения

Кафедра “Детали машин”

Ю.В. Даньшин

А.И. Поспелов

КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗУБЧАТЫХ

МЕХАНИЗМОВ

Методические указания для выполнения лабораторной работы

по “Теории механизмов и машин”

Хабаровск

2000

1

МПС РФ

Дальневосточный государственный

университет путей сообщения

Кафедра “Детали машин”

Ю.В. Даньшин

А.И. Поспелов

КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗУБЧАТЫХ

МЕХАНИЗМОВ

Методические указания для выполнения лабораторной работы

по “Теории механизмов и машин”

Хабаровск

2000

2

УДК 621.833-231.1 (075.8)

ББК К 44

Д 197

Рецензент:

Кандидат технических наук, заведующий кафедрой “Детали машин”

Хабаровского государственного технического университета

Фейгин А.В.

Даньшин Ю.В., Поспелов А.И.

Д 197 Кинематическое исследование зубчатых механизмов: Методические

указания для выполнения лабораторной работы по курсу “Теория

механизмов и машин”. - Хабаровск: Изд-во ДВГУПС, 2000. - 14 с.

Даны основные положения по кинематическому анализу зубчатых ме-

ханизмов аналитическим методом. Рассмотрена кинематика механизмов с

неподвижными осями, планетарных, дифференциальных, сдвоенных пла-

нетарных и замкнутых дифференциальных механизмов.

Для студентов механических специальностей всех форм обучения.

Рис. 7, список лит. 3 назв.

УДК 621.833-231.1 (075.8)

ББК К 44

 Издательство Дальневосточного государственного

университета путей сообщения (ДВГУПС), 2000

3

1. ВВЕДЕНИЕ. ОБЩИЕ СВЕДЕНИЯ

Целью работы является теоретическое и экспериментальное определе-

ние передаточных отношений зубчатых механизмов.

Передаточным отношением зубчатого механизма называется отношение

угловых скоростей его звеньев. При вычислении передаточного отношения

от звена j к звену k имеем

u

n

jk

j

k

j

k

j

k

= = =

ω

ϕ

, (1)

где ω - угловая скорость звена, с

-1

; n - частота вращения звена, мин

-1

;

ϕ - угол поворота звена за определенный промежуток времени.

Передаточное отношение от звена k к звену j

u

n

kj

k k

j

k

j

= = =

ω

ϕ

.

Очевидно, что между передаточными отношениями u

jk

и u

kj

существует

зависимость

u

jk

j

k k j kj

= = =

ω

ω ω ω

1 1

/

. (2)

Если колеса механизма вращаются в одной плоскости (или в парал-

лельных плоскостях), то имеет смысл различным направлениям вращения

колес присвоить знаки плюс или минус. Условимся положительным считать

вращение колеса, направленное против хода часовой стрелки. Тогда угло-

вая скорость ω

2

колеса 2 (см. рис.1,а) будет отрицательной. Поэтому пе-

редаточное отношение для внешнего зацепления двух колёс, выраженное

через радиусы начальных окружностей или числа зубьев колёс, также будет

отрицательным. При внутреннем зацеплении колеса вращаются в одну сто-

рону (рис.1,б)., передаточное отношение u

12

положительно.

Для механизмов с колёсами, вращающимися в непараллельных плоско-

стях, знак передаточного отношения в указанном смысле не имеет значе-

ния. В этом случае для определения направления вращения ведомого зве-

на используется специальные приёмы [1], [3].

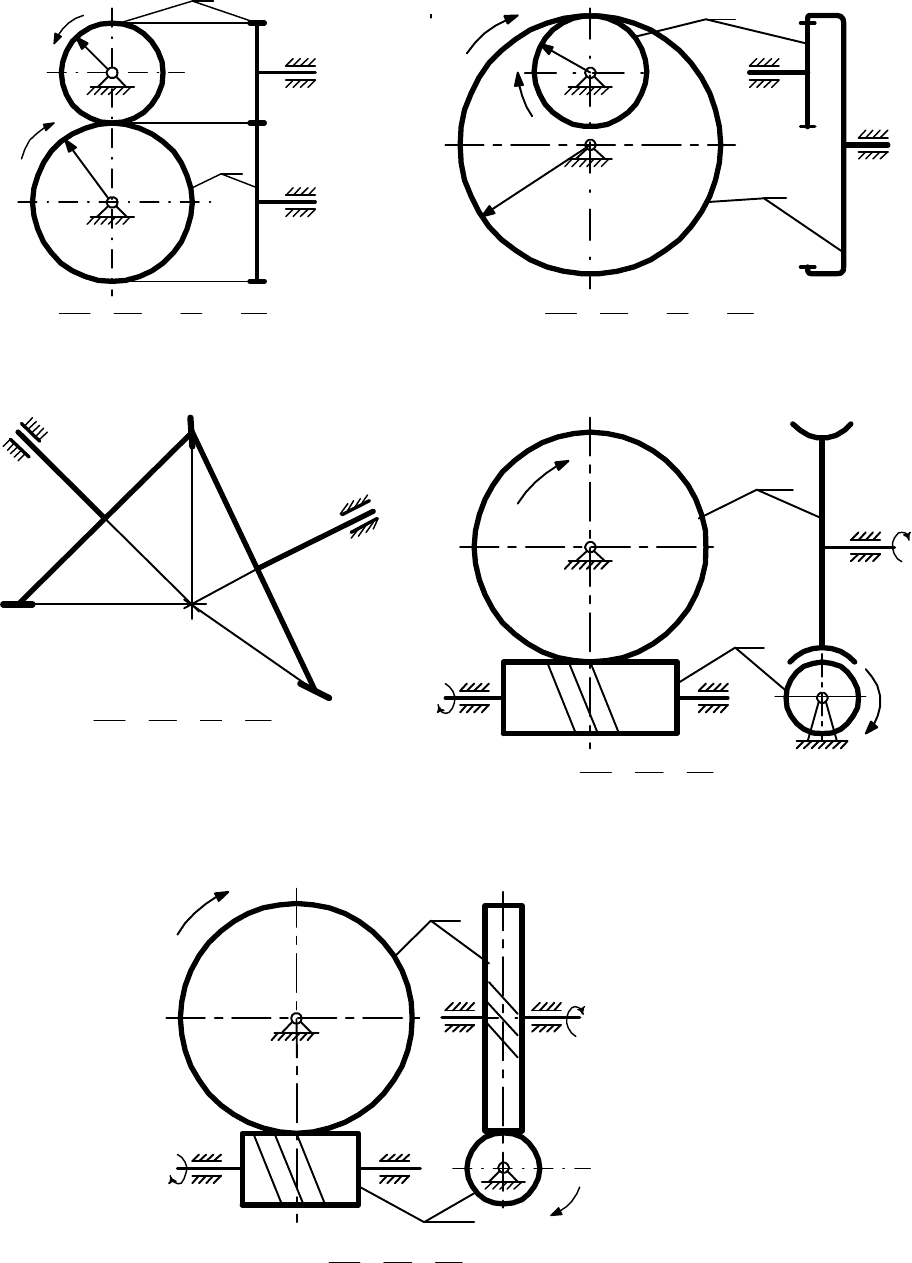
Зубчатые передачи с неподвижными осями колёс разделяются на про-

стые (одноступенчатые) и сложные (многоступенчатые). Простые

механизмы приведены на рис.1, здесь же указаны их передаточные отно-

шения, выраженные через числа зубьев колёс.

4

z

2

z

1

O

1

O

2

r

2

r

1

ω

1

ω

2

а) Внешнее зацепление

O

2

O

1

ω

2

ω

1

r

1

r

2

z

2

z

1

б) Внутреннее зацепление

O

2

O

1

r

2

r

1

z

2

z

1

в). Передача с коническими колесами

O

2

ω

2

ω

1

ω

2

ω

1

z

1

2

г). Червячная передача

O

2

ω

2

ω

1

O

1

ω

1

ω

к

z

2

z

1

д). Передача с винтовыми колесами

u

n

r

z

12

1

2

1

2

1

2

1

= = =+ =+

ω

u

n

r

z

12

1

2

1

2

1

2

1

= = = =

ω

u

n

r

z

12

1

2

1

2

1

2

1

= = =− =−

ω

u

n

z

12

1

2

1

2

1

= = =

ω

u

n

z

12

1

2

1

2

1

= = =

ω

1

2

1

2

1

2

1

Рис. 1. Простые (одноступенчатые) механизмы с неподвижными осями ко-

лес: r

1

, r

2

радиусы начальных окружностей колёс; z

1

, z

2

- числа зубьев ко-

лес.

5

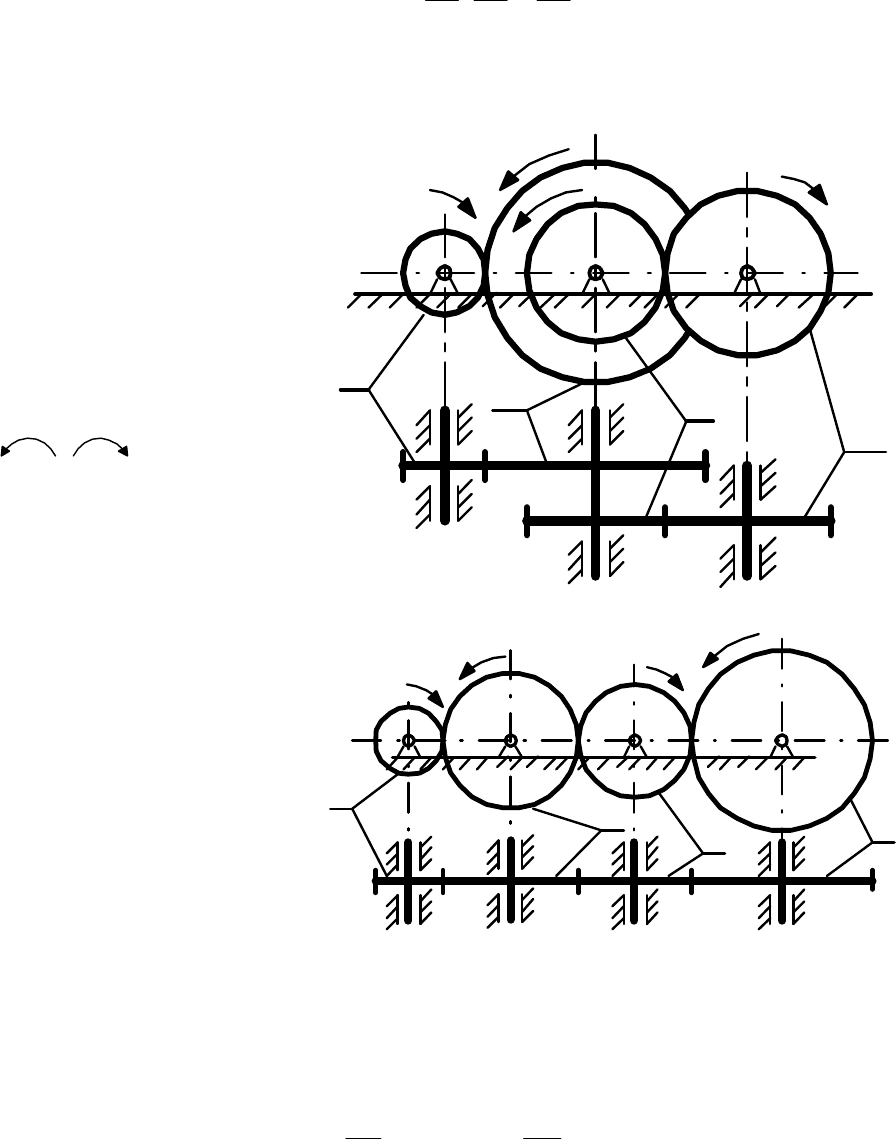
Сложные (многоступенчатые) передачи с неподвижными осями колёс

получаются при соединении нескольких одноступенчатых передач в один

механизм. Нетрудно убедиться, что передаточное отношение сложного

зубчатого механизма равно произведению передаточных отноше-

ний простых механизмов, входящих в его состав.

Для механизма со ступенчатым соединением колес (см. рис. 2,а)

u

14

=u u

12 34

1

2

3

4

1

4

⋅ = ⋅ =

ω

(3)

а)Ступенчатое соеди-

нение колес, в котором

ω

2

=ω

3

Знак

ω

+

-

ω

1

ω

2

ω

3

ω

4

z

3

z

1

z

2

z

4

1

2

3

4

б).

Рядовое

соединение

колес

ω

1

ω

2

ω

3

ω

4

O

1

O

2

O

3

O

4

z

1

z

2

z

3

z

4

1

2

3

4

Рис. 2. Сложные механизмы с неподвижными осями

Передаточное отношение в обратном направлении, т.е. от колеса 4 к ко-

лесу 1 будет

u

41

=

ω

4

1

43 21

14

1

= ⋅ =u u

u

.

6

Аналогично, для механизма с рядовым соединением колес (рис. 2,б),

имеем

u

14

=u u u

12 23 34

1

2

3

4

1

4

⋅ ⋅ = ⋅ ⋅ =

ω

. (4)

Обратим внимание читателя на то, что правило перемножения переда-

точных отношений справедливо только для механизмов, оси вращения ко-

торых неподвижны.

Выразив в формуле (4) передаточное отношение сложного механизма

через числа зубьев колес, получим знак общего передаточного отношения

u

14

=

ω

1

4

12 23 34

2

1

3

2

4

3

4

1

= ⋅ ⋅ =−













−













−













=−u u u

z

.

Знак минус указывает на то, что зубчатые колеса 1 и 4 вращаются в раз-

ные стороны, т.е. угловые скорости ω

1

и ω

4

по знаку противоположны. Это

видно также из рис. 2,б.

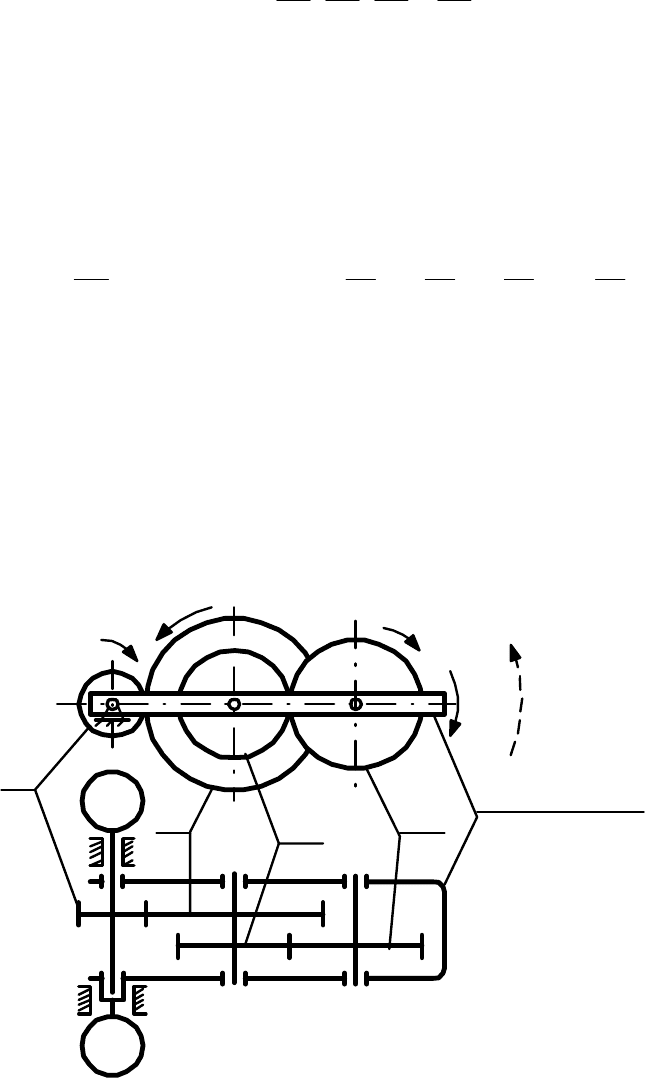
Если в механизме с неподвижными осями стойку привести во вращение

вокруг оси первого колеса, то такой механизм превратиться в дифферен-

циальный (см. рис. 3).

В нём стойка становится новым ведущим звеном - водилом, которое “во-

дит” оси колёс вокруг неподвижной оси 0

1

. Колесо, ось вращения которого

неподвижна, называется центральным колесом (например, колесо 1 на

рис. 3). Зубчатые колёса, оси вращения которых перемещаются по окружно-

сти, называются сателлитами. Степень подвижности дифференциально-

го механизма равна двум, т.к. в нём два ведущих звена - колесо 1 и водило

ω

1

ω

2

=ω

3

ω

4

ω

н

М

2

М

1

−ω

н

z

4

z

3

z

2

z

1

Водило Н

О

3

О

2

О

1

Рис. 3. Дифференциальный механизм

7

Н , которые приводятся во вращение от двух независимых друг от друга

двигателей М

1

и М

2

.

В дифференциальном механизме различают абсолютные и относитель-

ные угловые скорости звеньев. Абсолютные скорости колёс измеряются по

отношению к стойке, относительные - по отношению к водилу. Для кинема-

тического исследования дифференциального механизма используется ме-

тод обращения движения: мысленно всему механизму в целом задаётся

вращение вокруг оси центрального колеса с угловой скоростью, равной уг-

ловой скорости водила, но направленной в противоположную сторону. В та-

ком условном механизме водило Н становится неподвижным, т.к. его угло-

вая скорость будет равна ω

н

+(-ω

н

)=0. Поэтому оси 0

1

, 0

2

, 0

3

всех колёс ста-

нут неподвижными и дифференциальный механизм превратится в меха-

низм с неподвижными осями. Такой механизм называется преобразован-

ным. Угловые скорости колёс 1 и 4 в преобразованном механизме

ω

1

()н

=ω

1

-ω

н

, (5)

ω

4

(н)

=ω

4

-ω

н

, (6)

где ω

1

, ω

н,

ω

4

- абсолютные угловые скорости; ω

1

(н)

, ω

4

(н)

- относительные уг-

ловые скорости 1-го и 4-го колёс. В скобках принято указывать неподвижное

звено.

Передаточное отношение в преобразованном механизме от колеса 4 к

колесу 1:

u

н

41

4

1

4

1

()

.= =

−

ω

ω ω

(7)

Формула (7) называется формулой Виллиса.

Поскольку преобразованный механизм является механизмом с непод-

вижными осями, то его передаточное отношение u

41

(н)

можно вычислить по

известным числам зубьев колес

u u u

z

z z

н

41 43 21

3

4

1

2

1 3

2 4

()

.= ⋅ =−













−













=

⋅

(8)

При кинематическом исследовании дифференциального механизма уг-

ловые скорости ведущих звеньев ω

1

и ω

н

должны быть заданы. После оп-

ределения u

41

(н)

по формуле (8) в соотношении (7) остаётся одно неизвест-

ное - угловая скорость ω

4

ведомого колеса 4. Она легко может быть опре-

делена. После подсчётов, полученный знак ω

4

укажет направление враще-

ния этого колеса.

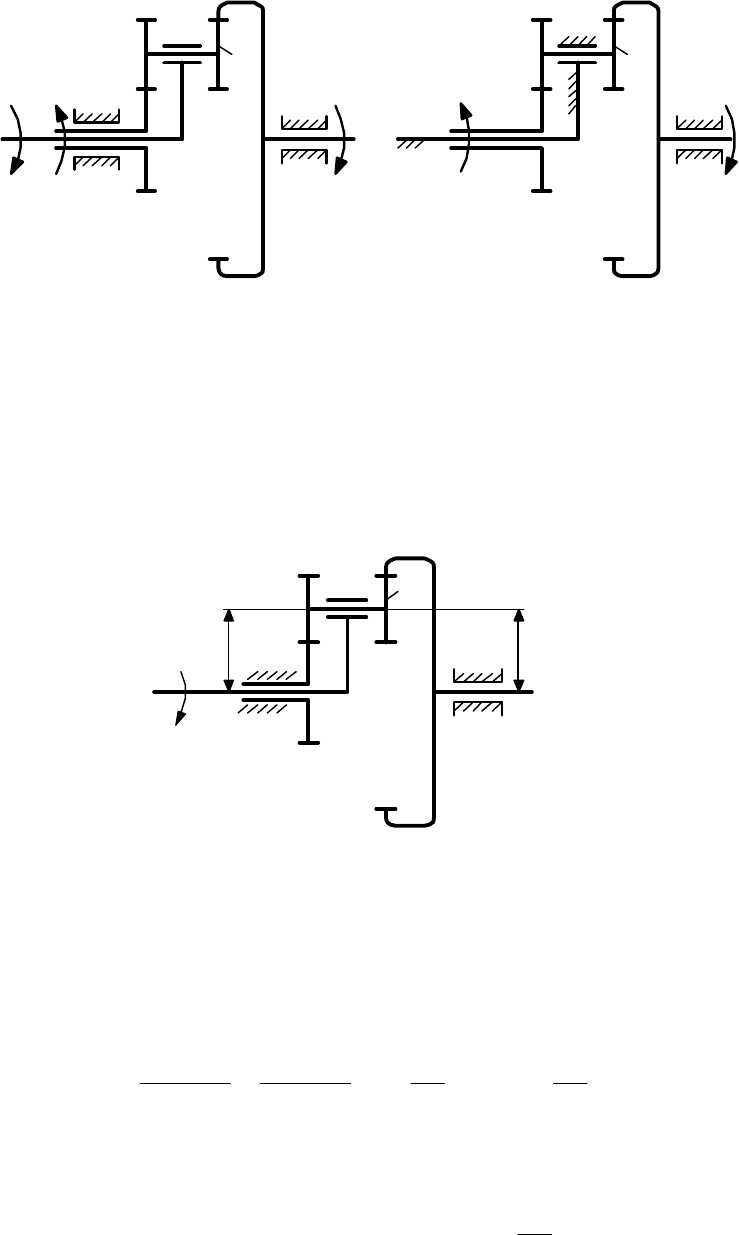
В технических устройствах используются соосные дифференциальные

механизмы, в которых оси ведущего колеса 1 и ведомого 4 совпадают (см.

рис. 4).

8

а) б)

ω

н

ω

4

z

2

H

z

3

z

1

z

4

ω

1

ω

4

(н)

=

ω

4

−ω

н

H

z

1

z

3

z

4

z

2

ω

1

(н)

=

ω

1

−ω

н

Рис. 4. Соосный дифференциальный механизм (а) и соответствующий ему

преобразованный механизм (б).

Если в рассмотренном дифференциальном механизме центральное ко-

лесо 1 сделать неподвижным, то дифференциальный механизм превра-

титься в планетарный (рис. 5).

Следовательно, планетарный механизм является частным случаем

дифференциального, и к нему можно применить все выводы, сделанные

для дифференциальных механизмов. Формула (7) для планетарного меха-

низма (ω

1

=0) примет вид:

u

н

н н

41

4

1

4 4

1

()

;=

−

=

−

=−













+

ω ω

ω

4

1

н

u













=−

()

.

Учитывая, что отношение абсолютных скоростей звеньев есть переда-

точное отношение планетарного механизма

ω

4

1

н

u













=

()

, получим

u u

н

4

1

4

1

()

= − , (9)

где u

н4

1()

- передаточное отношение планетарного механизма при ведомом

водиле и неподвижном колесе 1, т.е. в предложении, что передача движе-

ω

н

2

H

3

1

4

а

w34

а

w

12

Рис. 5. Соосный планетарный механизм

9

ния осуществляется от 4-го колеса к водилу. При этом , от единицы отнима-

ется передаточное отношение преобразованного механизма, которое все-

гда вычисляется от колеса 4 к колесу неподвижному (обратите на это вни-

мание).

Если же водило является ведущим звеном, то следует перейти к фор-

муле (9) по соотношению (2):

u

u u

н

4

1

4 4

4

1

41

1

()

() ()

/

.= = = =

−

ω

ω ω ω

(10)

В соосном механизме межосевые расстояния зацепляющихся колес

равны: а

w12

=a

w34

(см. рис. 5). Поэтому числа зубьев колёс должны соответ-

ствовать условию соосности

m

z z

m

z z

12

1 2

34

4 3

2

( ) ( ).+ = − (11)

При равных модулях зацепления m

12

=m

34

условие соосности (11) примет

вид:

z

1

+z

2

=z

4

-z

3

.

Условие соосности можно использовать для определения числа зубьев

одного из колёс по известным числам зубьев трёх остальных.

Как одноступенчатые механизмы могут образовывать многоступенчатые

передачи (см. рис. 2), так и планетарные механизмы могут составлять

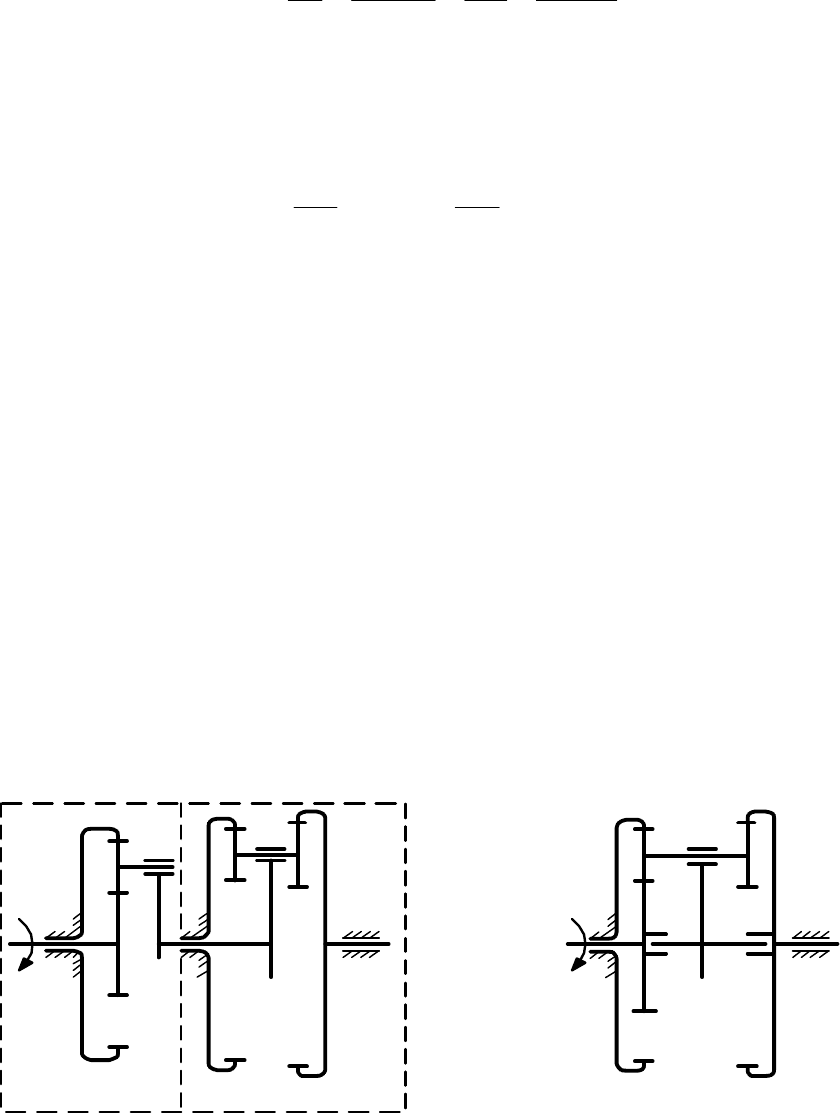
сложные механизмы. На рис. 6,а изображена схема сложного механизма,

состоящего из двух планетарных механизмов. Первым планетарный меха-

низм состоит из колес 1, 2, 3 и ведомого водила Н, а второй - из ведущего

водила Н′

и колёс 2′, 3′, 4, 5. Водило Н первого механизма наглухо прикреп-

лено к водилу Н′ второго, т.е. ω

н

=ω

н′

.

а) Два последовательно включенных

планетарных механизма

б) Сдвоенный планетарный меха-

низм

1-й механизм 2-й механизм

Н`

Н

1

2

3

3`

2` 4

5

Н

z

3

z

4

z

5

ω

1

ω

1

z

2

z

1

Рис. 6. Сложные планетарные механизмы

Даньшин Ю.В., Поспелов А.И. Кинематическое исследование зубчатых механизмов

Подождите немного. Документ загружается.