Даньшин Ю.В., Поспелов А.И. Кинематическое исследование зубчатых механизмов
Подождите немного. Документ загружается.

10
Для определения общего передаточного отношения u
15
сдвоенного
планетарного механизма перемножим передаточные отношения входящих в
него механизмов:
u u u
н
н
15 1
3
5
3
= ⋅
′
′
() ( )
. (12)
Передаточное отношение 1-го планетарного механизма u
1
3
н
()
при ведо-
мом водиле Н по соотношению (9) будет
u u u u
z
z
z
z
z
z
z z
z
н
н
1
3
13 12 23
2
1
3
2
3
1
1 3
1
1 1 1 1
() ()
.=− =− ⋅ =−−
+
=+ =
+
(13)
Передаточное отношение u
′
′
н 5
3( )
2-го планетарного механизма при веду-
щем водиле Н
′
по соотношению (10) равно
u
u u
u u
z
z
z
z
zz
zz
z
z
zz zz
н
н
н
′
′
′
′
′
′
′′
′
′
′
′
′
′ ′
= =
−
=
− ⋅
=
−
=
−
=
−
5
3
5
3
53
54 23
4
5
3
2
43
52
2 5
2 5 3 4
1
1
1
1
1
1
1
1
1
( )
( ) ( )
. (14)
Подставив (13) и (14) в (12), окончательно получим:
u
z
z
z
z
zzz zz
15
1 3 2 5
1 2 5 3 4
=
+
⋅
−
′
′ ′
(
)
( )
. (15)
Если конструктивно механизм выполнить так, чтобы
z
2
=z
2′
, z
3
=z
3′
, (16)
то можно получить сдвоенный планетарный механизм, изображенный на
рис. 6,б. Его передаточное отношение определяется по формуле (15) с уче-
том (16).
Развитие структуры планетарного механизма в радиальном направлении
приводит к бипланетарным механизмам. Бипланетарный механизм со-
стоит из основного планетарного механизма и сателлитного планетарного
механизма. При этом последний связывает между собой сателлиты основ-
ного механизма так, что они входят в сателлитный планетарный механизм,
имеющий собственное водило. Степень подвижности планетарного меха-
низма равна единице, т.е. для его функционирования требуется один двига-
тель. Подробнее о бипланетарных механизмах - см. [3].
Если в дифференциальном механизме (W=2) звенья соединить (замк-
нуть) зубчатой цепью со степенью подвижности W= -1, то получим замкну-
тый дифференциальный механизм. Степень подвижности всего механиз-
ма станет равной единице. При кинематическом исследовании замкнутого
дифференциального механизма следует сначала выделить его составные
11
части. Замыкающую цепь в конструкции механизма найти проще, т.к. она
обычно представляет собой зубчатую передачу с неподвижными осями ко-
лес. Затем для дифференциального механизма следует записать формулу
Виллиса (7), а для замыкающей цепи, как зубчатой передачи с неподвиж-
ными осями, - соотношение типа (4). После этого из полученной системы
двух уравнений можно определить требуемое передаточное отношение.
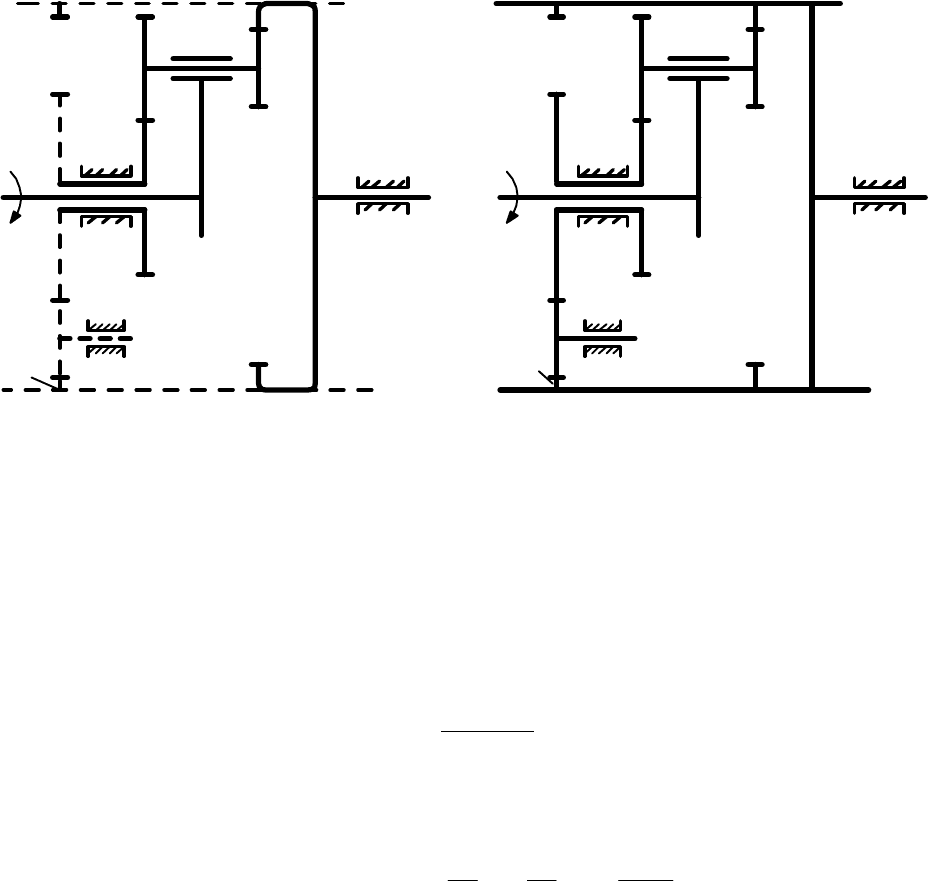
В качестве примера рассмотрим дифференциальный механизм, изобра-
жённый на рис. 4,а. Добавим к нему замыкающую кинематическую цепь, со-
стоящую из зубчатых колёс с числами зубьев z
5
, z
6
и z
7
. Эта цепь на рис. 7,а
показана штриховой линией. Колесо z
5
цепи жестко связано к центральным
колесом z
1
дифференциального механизма, а колесо z
7
- с центральным
колесом z
4
. Поэтому в замкнутом дифференциальном механизме (рис. 7,б)
выполняются соотношения
ω
1
=ω
5
, ω
4
=ω
7
. (17)
ω
н
z
3
z
1
z
2
z
4
ω
н
z
3
z
1
z
2
z
4
z
5
z
6
z
7
Н
z
5
z
6
z
7
Н
а) Схема образования механизма б) Схема замкнутого дифференциаль-
ного механизма
Рис. 7. Замкнутый дифференциальный механизм
Пусть заданы числа зубьев всех колёс и требуется определить переда-
точное отношение u
н4
=ω
н
/ω
4
замкнутого дифференциального механизма. По
формуле Виллиса (7) для дифференциального механизма имеем
u
н
н
н
41
4
1
()
,=
−
−
ω
ω
ω ω
(18)
где
u u u
z
z
z
z
zz
zz
н
41 43 21
3
4
1
2
13
24
()
.= ⋅ =
−
=− (19)
12
Для замыкающей цепи, как для зубчатого механизма с неподвижными
осями, можно записать
ω
ω
ω
ω
1
4
5
7
57
= = u , (20)
где передаточное отношение u
57
известно:
u u u
z
z
z
z
z
z
57
56 67
6
5
7
6
7
5
= ⋅ =−
+
=− . (21)
Соотношение (18) запишем в виде
ω ω
ω
ω
н
н н
u u( ) ( ),
() ()
1 1
41
4
1
4
41
− = −
или, с учетом (20),
ω
ω
н
н
н
u u
u
4
57
41
41
1
1
=
− ⋅
−
()
()
. (22)
Подставив (19) и (21) в соотношение (22), найдем искомое передаточное
отношение замкнутого дифференциального механизма
u
z
z
z
z
z
z
z zz zz
н
н
4
4
245 137
5 24 13
= =
−
+
ω
ω ( )
.
2. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
2.1. По заданной модели вычертить схему механизма. Для планетарного
и дифференциального механизма следует начертить также схему преобра-
зованного механизма.
2.2. Записать формулу и вычислить передаточное отношение механиз-
ма.
2.3. Определить передаточное отношение механизма экспериментально.
Для этого следует повернуть ведущее звено на любое количество оборотов
в положительном направлении и замерить угол поворота ведомого звена.
По формуле (1) подсчитать передаточное отношение и сопоставить его с
найденным ранее.
13
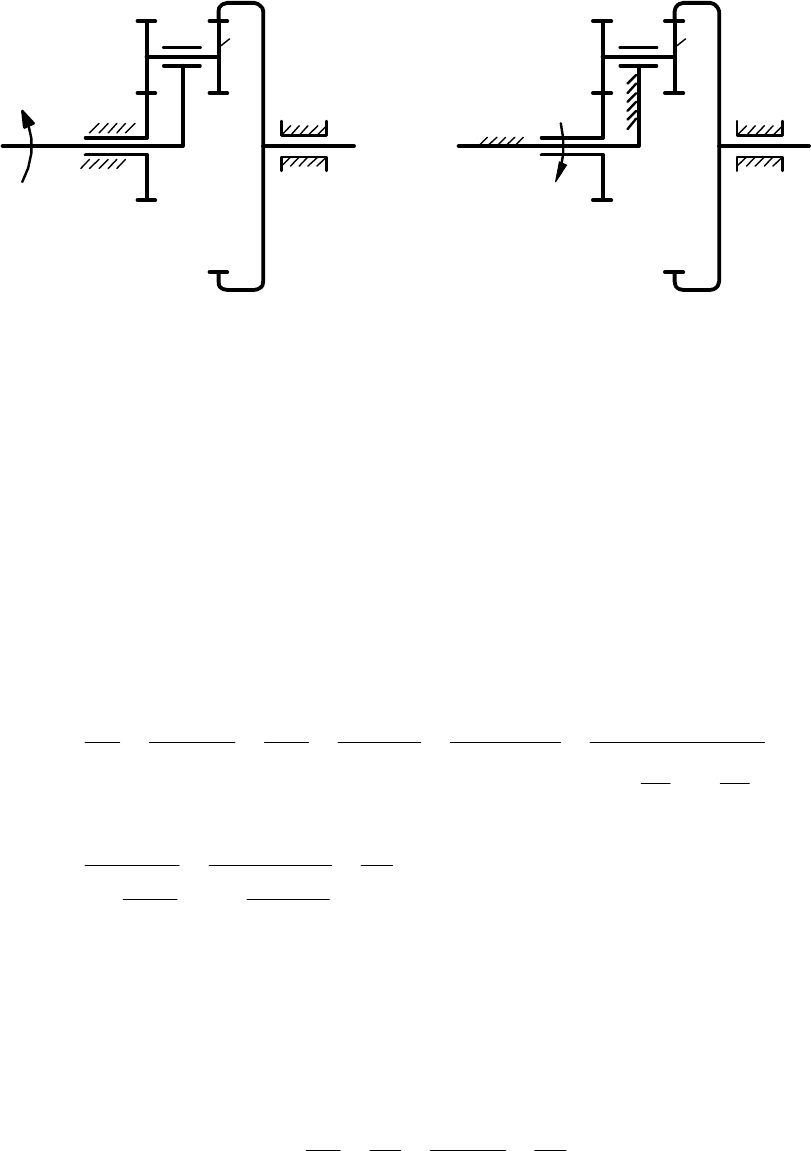
Пример:
1. Схема механизма
ω
н
z
2
H
z
3
z
1
z
4
ω
1
(
н)
=
-
ω
н
2
H
3
1
4
ω
н
=0
z
1
=60,
z
2
=30,
z
3
=60.
а). Планетарный механизм
б). Преобразованный планетарный
механизм
2. По условию соосности (11) определяем число зубьев Z
4
центрального
колеса:
z
4
=z
1
+z
2
+z
3
=60+30+60=150.
Так как ведущим звеном является водило Н (на cхеме ведущее звено
помечается круговой стрелкой), то передаточное отношение находим по
формуле (10):
u
u u
uu
z
z
z
z
zz
zz
н
н
н
н
н
4
1
4 4
4
1
41
43
21
3
4
1
2
13
24
1 1 1
1
1
1
1
1
1
1
1
1
6060
30150
1
18
()
() ()
/
,
.
= = = =
−
=
−
=
−
−
=
=
+
=
+
⋅
⋅
=
ω
ω ω ω
Знак плюс, полученный в передаточном отношении, свидетельствует о
том, что водило и колесо 4 будут вращаться в одну сторону.
3. Выразим передаточное отношение через углы поворота звеньев:
u
н
н н
4
1
4 4
360
650
1
18
()
,
,= = =
+
+
≈
ω
ω
ϕ
ϕ
o
o
где угол поворота ведущего водила был принят равным +360
°
. При этом ве-
домое колесо 4 повернулось на угол 650
°
также против хода часовой стрел-
ки.
14
Сравнение величин передаточного отношения механизма в п. 2 и 3 пока-
зывает, что результаты аналитического подсчета и практического опреде-
ления передаточного отношения в приделах точности эксперимента совпа-
дают.
ЛИТЕРАТУРА
1. Артоболевский И.И. Теория механизмов и машин: Учеб. для втузов. -
4-е изд., перераб. и доп. - М.: Гл. ред. физ.- мат. лит., 1988. - 640 с.
2. Артоболевский И.И., Эдельштейн Б.В. Сборник задач по теории меха-
низмов и машин.-М.: Гл. ред. физ.- мат. лит., 1973. - 256 с.
3. Теория механизмов и машин: Учеб. для втузов / К.В. Фролов, С.А. По-
пов, А.К. Мусатов и др.; Под ред. К.В. Фролова. - М.: Высш. шк., 1987. -
496 с.
ОГЛАВЛЕНИЕ
1.
Введение. Общие сведения................................................................ 3
2.
Порядок выполнения лабораторной работы.......................................
12
Литература.......................................................................................... 14
15
Поз. 1.15
План 2000 г.
Даньшин Юрий Викторович,
Поспелов Александр Иванович.
КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗУБЧАТЫХ МЕХАНИЗМОВ.
Методические указания для выполнения лабораторной работы по “Тео-
рии механизмов и машин”
* * *
Подписано в печать
Лицензия ЛР 02068 от 1 августа 1996 г.
Печать офсетная. Бумага №2. Формат 60×84/16.
Усл. печ. листов 0,9. Зак. 35. Тираж 250 экз.
Цена 4 р.
* * *
Издательство ДВГУПС
16
680021, г. Хабаровск, ул. Серышева, 47.
