Damodaran A. Applied corporate finance

Подождите немного. Документ загружается.

Mean =

= X

j=1

j= n

• The median, which is the mid-point of the series; half the data in the series is higher

than the median and half is lower

• The variance, which is a measure of the spread in the distribution around the mean,

and is calculated by first summing up the squared deviations from the mean, and then

dividing by either the number of observations (if the data represents the entire

population) or by this number, reduced by one (if the data represents a sample)

Variance =

= (X

)

j=1

j= n

The standard deviation is the square root of the variance.

The mean and the standard deviation are the called the first two moments of any data

distribution. A normal distribution can be entirely described by just these two moments;

in other words, the mean and the standard deviation of a normal distribution suffice to

completely characterize it. If a distribution is not symmetric, it is considered to be skewed

and the skewness is the moment that describes both the direction and the magnitude of

the skewness.

Looking for Relationships in the Data

When there are two series of data, there are a number of statistical measures that

can be used to capture how the two series move together over time.

Correlations and Covariances

The two most widely used measures of how two variables move together (or do

not) are the correlation and the covariance. For two data series, X (X

, X

,.) and Y(Y,Y...

), the covariance provides a non-standardized measure of the degree to which they move

together, and is estimated by taking the product of the deviations from the mean for each

variable in each period.

Covariance =

= (X

) (Y

)

j=1

j= n

The sign on the covariance indicates the type of relationship that the two variables have.

A positive sign indicates that they move together and a negative that they move in

opposite directions. While the covariance increases with the strength of the relationship,

it is still relatively difficult to draw judgments on the strength of the relationship between

two variables by looking at the covariance, since it is not standardized.

The correlation is the standardized measure of the relationship between two

variables. It can be computed from the covariance –

Correlation =

) (Y

)

j=1

j= n

)

j=1

j=n

j=1

j=n

)

The correlation can never be greater than 1 or less than minus 1. A correlation close to

zero indicates that the two variables are unrelated. A positive correlation indicates that

the two variables move together, and the relationship is stronger the closer the correlation

gets to one. A negative correlation indicates the two variables move in opposite

directions, and that relationship also gets stronger the closer the correlation gets to minus

1. Two variables that are perfectly positvely correlated (r=1) essentially move in perfect

proportion in the same direction, while two assets which are perfectly negatively

correlated move in perfect proportion in opposite directions.

Regressions

A simple regression is an extension of the correlation/covariance concept. It

attempts to explain one variable, which is called the dependent variable, using the other

variable, called the independent variable.

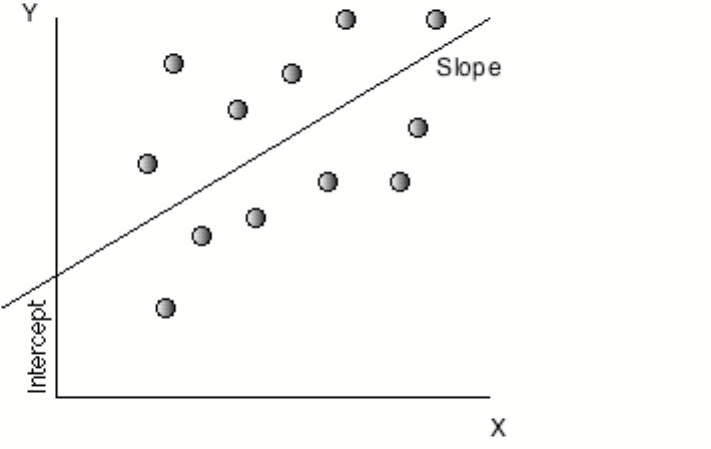
Scatter Plots and Regression Lines

Keeping with statistical tradition, let Y be the dependent variable and X be the

independent variable. If the two variables are plotted against each other, with each pair of

observations representing a point on the graph, you have a scatter plot, with Y on the

vertical axis and X on the horizontal axis.

In a regression, we attempt to fit a line through the points that best fits the . In its

simplest form, this is accomplished by finding a line that minimizes the sum of the

squared deviations of the points from the line. Consequently, it is called ordinary least

squares (OLS) regression. When such a line is fit, two parameters emerge – one is the

point at which the line cuts through the Y-axis, called the intercept of the regression, and

the other is the slope of the regression line.

Y = a + b X

The slope (b) of the regression measures both the direction and the magnitude of the

relationship between the dependent variable (Y) and the independent variable (X). When

the two variables are positively correlated, the slope will also be positive, whereas when

the two variables are negatively correlated, the slope will be negative. The magnitude of

the slope of the regression can be read as follows - for every unit increase in the

dependent variable (X), the independent variable will change by b (slope).

Estimating Regression Parameters

While there are statistical packages that allow us to input data and get the

regression parameters as output, it is worth looking at how they are estimated in the first

place. The slope of the regression line is a logical extension of the covariance concept

introduced in the last section. In fact, the close linkage between the slope of the

regression and the correlation/covariance should not be surprising since the slope is

estimated using the covariance –

Slope of the Regression = b =

Covariance

Variance of X

The intercept (a) of the regression can be read in a number of ways. One interpretation is

that it is the value that Y will have when X is zero. Another is more straightforward, and

is based upon how it is calculated. It is the difference between the average value of Y,

and the slope adjusted value of X.

Intercept of the Regression = a =

- b * (

)

Regression parameters are always estimated with some error or statistical noise, partly

because the relationship between the variables is not perfect and partly because we

estimate them from samples of data. This noise is captured in a couple of statistics. One is

the R-squared of the regression, which measures the proportion of the variability in the

independent variable (Y) that is explained by the dependent variable (X). It is a direct

function of the correlation between the variables –

R - squared of the Regression = Correlation

An R-squared value closer to one indicates a strong relationship between the two

variables, though the relationship may be either positive or negative. Another measure of

noise in a regression is the standard error, which measures the "spread' around each of the

two parameters estimated- the intercept and the slope. Each parameter has an associated

standard error, which is calculated from the data –

Standard Error of Intercept = SE

( X

) (Y

" bX

)

j=1

j= n

(

)

j=1

j=n

(n "1) (X

)

j=1

j= n

Standard Error of Slope = SE

" bX

)

j=1

j= n

(

)

(n "1) (X

)

j=1

j= n

If we make the additional assumption that the intercept and slope estimates are normally

distributed, the parameter estimate and the standard error can be combined to get a "t

statistic" that measures whether the relationship is statistically significant.

T statistic for intercept = a/SE

T statistic from slope = b/SE

For samples with more than 120 observations, a t statistic greater than 1.66 indicates that

the variable is significantly different from zero with 95% certainty, while a statistic

greater than 2.36 indicates the same with 99% certainty. For smaller samples, the t

statistic has to be larger to have statistical significance.

Using Regressions

While regressions mirror correlation coefficients and covariances in showing the

strength of the relationship between two variables, they also serve another useful purpose.

The regression equation described in the last section can be used to estimate predicted

values for the dependent variable, based upon assumed or actual values for the

independent variable. In other words, for any given Y, we can estimate what X should be:

X = a + B (Y)

How good are these predictions? That will depend entirely upon the strength of the

relationship measured in

From Simple to Multiple Regressions

The regression that measures the relationship between two variables becomes a

multiple regression when it is extended to include more than one independent variables

(X1,X2,X3,X4..) in trying to explain the dependent variable Y. While the graphical

presentation becomes more difficult, the multiple regression yields output that is an

extension of the simple regression.

Y = a + b X1 + c X2 + dX3 + eX4

The R-squared still measures the strength of the relationship, but an additional R-squared

statistic called the adjusted R squared is computed to counter the bias that will induce the

R-squared to keep increasing as more independent variables are added to the regression.

If there are k independent variables in the regression, the adjusted R squared is computed

as follows –

The actual values that t statistics need to take on can be found in a table for the t distribution, which is

reproduced at the end of this book as an appendix.

R squared =

" bX

)

j=1

j= n

(

)

n - 1

Adjusted R squared =

" bX

)

j=1

j= n

(

)

n - k

Multiple regressions are powerful weapons that allow us to examine the determinants of

any variable.

Regression Assumptions and Constraints

Both the simple and multiple regressions that we have described in this section

also assume linear relationships between the dependent and independent variables. If the

relationship is not linear, we have two choices. One is to transform the variables, by

taking the square, square root or natural log (for example) of the values and hope that the

relationship between the transformed variables is more linear. The other is run non-linear

regressions that attempt to fit a curve through the data.

There are implicit statistical assumptions behind every multiple regression that we

ignore at our own peril. For the coefficients on the individual independent variables to

make sense, the independent variable needs to be uncorrelated with each other, a

condition that is often very difficult to meet. When independent variables are correlated

with each other, the statistical hazard that is created is called multicollinearity. In its

presence, the coefficients on independent variables can take on unexpected signs

(positive instead of negative, for instance) and unpredictable values.

There are simple diagnostic statistics that allow us to measure how far the data

that we are using in a regression may be deviating from our ideal. If these statistics send

out warning signals, we ignore them at our own peril.

Conclusion

In the course of trying to make sense of large amounts of contradictory data, there

are useful statistical tools that we can draw on. While we have looked at the only most

basic ones in this chapter, there are far more sophisticated and powerful tools that we can

draw on.

APPENDIX 2

FINANCIAL STATEMENTS

Financial statements provide the fundamental information that we use to analyze

and answer valuation questions. It is important, therefore, that we understand the

principles governing these statements by looking at four questions:

• How valuable are the assets of a firm? The assets of a firm can come in several forms

– assets with long lives such as land and buildings, assets with shorter lives such

inventory, and intangible assets that still produce revenues for the firm such as patents

and trademarks.

• How did the firm raise the funds to finance these assets? In acquiring these assets,

firms can use the funds of the owners (equity) or borrowed money (debt), and the mix

is likely to change as the assets age.

• How profitable are these assets? A good investment, we argued, is one that makes a

return greater than the hurdle rate. To evaluate whether the investments that a firm

has already made are good investments, we need to estimate what returns we are

making on these investments.

We will look at the way accountants would answer these questions, and why the answers

might be different when doing valuation. Some of these differences can be traced to the

differences in objectives – accountants try to measure the current standing and immediate

past performance of a firm, whereas valuation is much more forward looking.

The Basic Accounting Statements

There are three basic accounting statements that summarize information about a

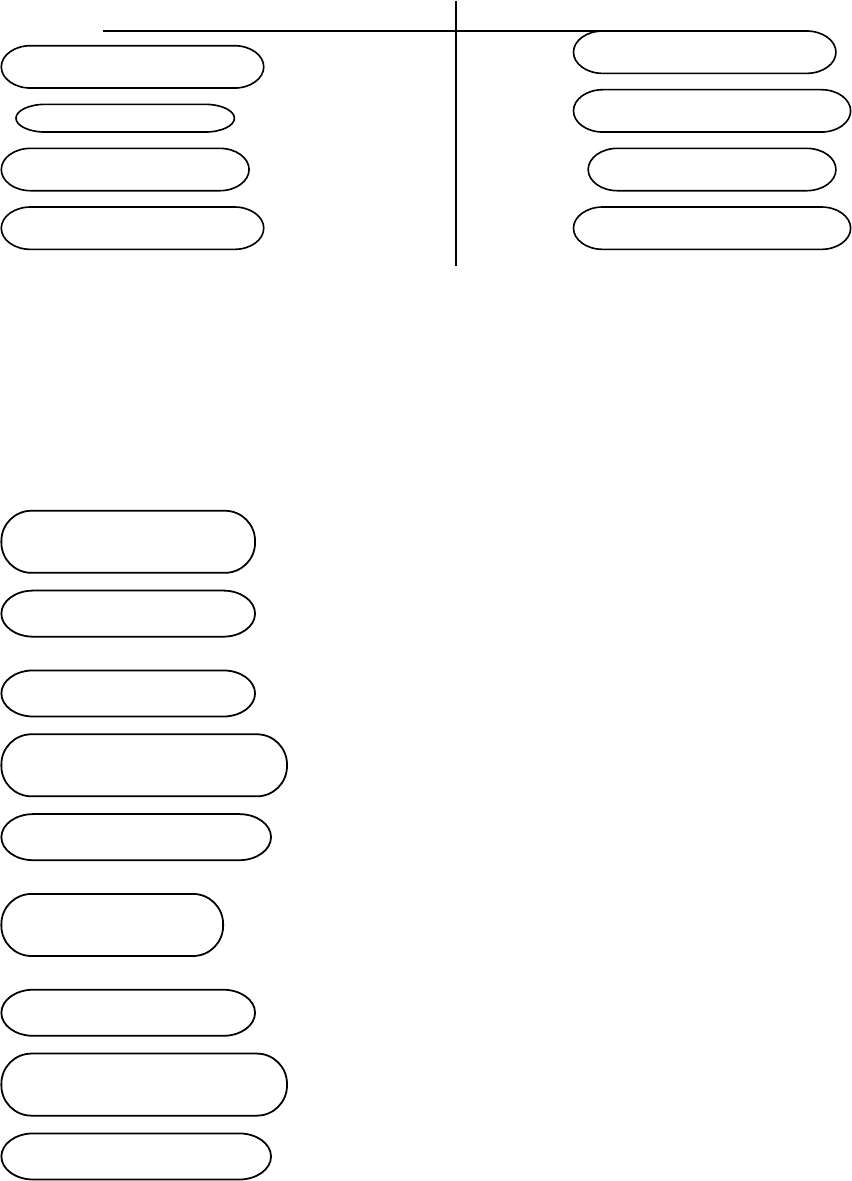
firm. The first is the balance sheet, shown in Figure 3.1, which summarizes the assets

owned by a firm, the value of these assets and the mix of financing, debt and equity, used

to finance these assets at a point in time.

Assets

Liabilities

Fixed Assets

Debt

Equity

Short-term liabilities of the firm

Intangible Assets

Long Lived Real Assets

Assets which are not physical,

like patents & trademarks

Current Assets

Financial Investments

Investments in securities &

assets of other firms

Short-lived Assets

Equity investment in firm

Debt obligations of firm

Current

Liabilties

Other

Liabilities

Other long-term obligations

Figure 1: The Balance Sheet

The next is the income statement, shown in Figure 3.2, which provides information on

the revenues and expenses of the firm, and the resulting income made by the firm, during

a period. The period can be a quarter (if it is a quarterly income statement) or a year (if it

is an annual report).

Figure 2: Income Statement

Revenues

Gross revenues from sale

of products or services

- Operating Expenses

Expenses associates with

generating revenues

= Operating Income

Operating income for the

period

- Financial Expenses

Expenses associated with

borrowing and other financing

- Taxes

Taxes due on taxable income

= Net Income before extraordinary items

Earnings to Common &

Preferred Equity for

Current Period

- (+) Extraordinary Losses (Profits)

Profits and Losses not

associated with operations

- Income Changes Associated with Accounting Changes

Profits or losses associated

with changes in accounting

rules

- Preferred Dividends

Dividends paid to preferred

stockholders

= Net Income to Common Stockholders

Finally, there is the statement of cash flows, shown in figure 3.3, which specifies the

sources and uses of cash of the firm from operating, investing and financing activities,

during a period.

Cash Flows From Operations

+ Cash Flows From Investing

+ Cash Flows from Financing

Net cash flow from operations,

after taxes and interest expenses

Includes divestiture and acquisition

of real assets (capital expenditures)

and disposal and purchase of

financial assets. Also include

acquisition of other firms.

Net cash flow from the issue and

repurchase of equity, from the

issue and repayment of debt and after

dividend payments

= Net Change in Cash Balance

Figure 3: Statement of Cash Flows

The statement of cash flows can be viewed as an attempt to explain how much the cash

flows during a period were, and why the cash balance changed during the period.

Asset Measurement and Valuation

When analyzing any firm, we would like to know the types of assets that it owns,

the values of these assets and the degree of uncertainty about these values. Accounting

statements do a reasonably good job of categorizing the assets owned by a firm, a partial

job of assessing the values of these assets and a poor job of reporting uncertainty about

asset values. In this section, we will begin by looking at the accounting principles

underlying asset categorization and measurement, and the limitations of financial

statements in providing relevant information about assets.

Accounting Principles Underlying Asset Measurement

An asset is any resource that has the potential to either generate future cash

inflows or reduce future cash outflows. While that is a general definition broad enough to

cover almost any kind of asset, accountants add a caveat that for a resource to be an asset.