Цветков В.Я. Геоинформационные системы и технологии
Подождите немного. Документ загружается.


Рассмотрим наиболее общие классы проекционных
преобразований [2] для решения задач в ГИС.
Преобразования картографических проекций применяют для
перехода от исходной (хранимой в базе данных) картографической
композиции к задаваемой пользователем. В частности, когда
цифровая карта (слой), выполненная в известной проекции и
соответствующая ее теоретическим координатам, должна быть
преобразована в географические координаты либо в другую
картографическую проекцию.
Достоинством моделирования в ГИС является возможность
трансформирования космического (или аэро-) снимка
непосредственно в картографическую проекцию, минуя построение
фотограмметрической модели или традиционное
фотограмметрическое трансформирование снимков. Эта
возможность предоставляется в пакетах ГИС, в первую очередь
связанных с обработкой данных дистанционного зондирования.
Выделение подгруппы преобразования проекций связано с
необходимостью интефации данных из различных
картофафических источников с разнородной математической
основой. Карты могут отличаться моделью Земли, примененной
при создании карты; картографической проекцией; системой
координат, привязанной к используемой модели Земли.
Технологически для проекционных преобразований в ГИС
необходимо создать файл описания картографической проекции и
выбрать исходный файл. Из набора типов преобразований
выбирают необходимое, задают требуемые параметры, и
проекционное преобразование осуществляется автоматически
путем создания новой картографической проекции в заданном слое
и соответствующем файле.
Проекционные преобразования требуют рассмотрения
различных классов проекций, применяемых для создания карт[2].
Картографические проекции классифицируют по различным
признакам, например в зависимости от характера и размера
искажений.
Равноугольные проекции (conformal projection) сохраняют без
искажений углы и формы малых объектов, но в них резко
деформируются длины и площади объектов. В математике такие
преобразования называют конформными.
Равновеликие проекции (equivalente projection) не искажают
площадей, но в них искажены углы и формы объектов. Первый вид
проекций приемлем для прокладки маршрутов транспортных
средств, второй -для определения площадей и землепользования.
Произвольные проекции (arbitrary projection) имеют искажения
углов, площадей и длин, но эти искажения распределены по карте,
напри
мер,
так,
124

что минимальные искажения имеются в центральной части и
возрастают к краям. Среди произвольных проекций выделяют
равнопрамежуточные (equidistant projection), в которых
искажения длин отсутствуют по одному из направлений: вдоль
меридиана или вдоль параллели.
Конические проекции (konical projection). По характеру
искажений конические проекции могут быть различными.
Наибольшее распространение получили равноугольные и
равнопромежуточные проекции.
Образование конических проекций можно представить как
проектирование земной поверхности на боковую поверхность
конуса, определенным образом ориентированного относительно
земного шара (эллипсоида) (рис. 5.1, а). В прямых конических
проекциях оси земного шара и конуса совпадают. При этом конус
берется или касательный, или
секущий.
После проектирования боковая поверхность конуса
разрезается по одной из образующих и развертывается в
плоскость (рис. 5.1, б). При проектировании по методу линейной
перспективы получаются перспективные конические проекции,
обладающие только промежуточными свойствами по характеру
искажений.
Другой метод образования конических проекций -
аналитический. В его основу положены уравнения проекций,
вытекающие из их определения и формулы общей теории
искажений. В конических проекциях имеются две постоянные
проекции а и с. Постоянная а равняется синусу широты
стандартной параллели или, что то же самое, синусу угла при
вершине конуса.
В зависимости от размеров изображаемой территории в
конических проекциях принимаются одна или две параллели,
вдоль которых сохраняются длины без искажений. Одна
параллель (касательная) принимается при небольшом протяжении
по сироте; две параллели (секущие) -при большом протяжении
для уменьшения уклонений масштабов от единицы. В литературе
их называют стандартными параллелями.
Коническая проекция данной группы вполне определяется,
если заданы постоянные проекции или любые величины, с ними
связанные. Это могут быть широты стандартных или крайних
параллелей. В последнем случае, например, может быть
дополнено условие, чтобы масштабы на крайних параллелях и на
параллели с наименьшим масштабом были равны по абсолютной
величине.
Азимутальные проекции (azimuthal projection). В них
парал
лели
(альм
укант
араты
)
изобр
ажаю
тся
конце
нтрич
еским
и
окру
жност
ями, а
мерид
ианы
(верт
икал
ы) -
пучко
м
прям
ых,
исход
ящих
из
центр
а
(рис.
5.2,
а).
125
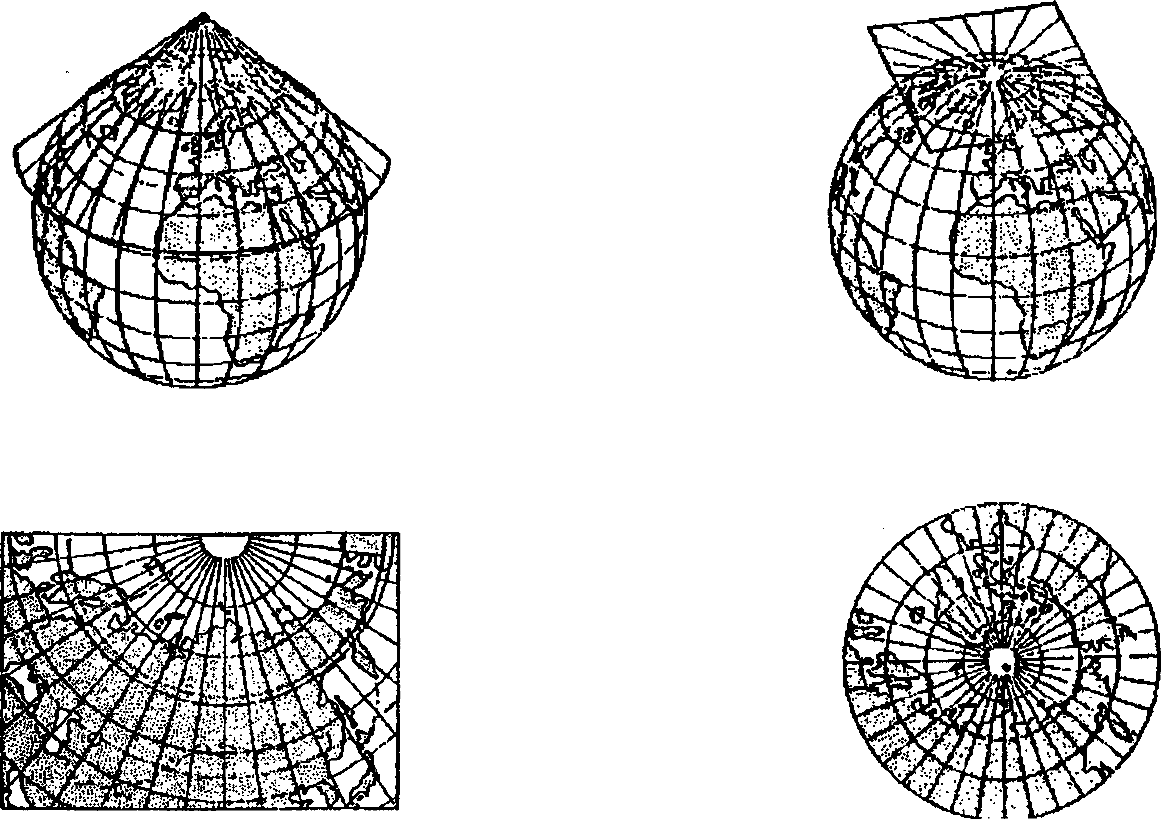
а

Рис. 5.1. Коническая
проекция:
а - принцип построения
проекции;
б - вид проекции
Рис. 5.2. Азимутальная
проекция:
а - принцип построения
проекции;
б - вид проекции
Углы между меридианами проекции равны
соответствующим па, ностям долго, Промежутки между
параллелями определяются принятым характером изображения
(равноугольным или другими способом проектирования точек
земной поверхности на картинную плоскость.
Нормальная сетка азимутальных проекций ортогональна. Их
мож-но рассматривать как частный случай конических
проекций, в которых а=1. Применяются прямые, косые и
поперечные азимутальные проекции, что определяется широтой
центральной точки проекции, выбор которой зависит от
расположения
территорий. Меридианы и параллели в косых и поперечных
проекциях изображаются кривыми линиями,
за исключением среднего мередиана, на котором находится
центральная точка проекции. В поперечных проекциях
прямо изображается также экватор: он является второй осью
семетрии.
В зависимости от искажений азимутальные проекции
подразделяются на
равноугольные, равновеликие и с промежуточными свойствами.
В проекции масштаб длин может сохранятся в точке или в одной
их параллелей (вдоль альмукантарата).
В первом случае предполагается касательная картинная
плоскость, во втором - секущая. В прямых проекциях формулы
даются для поверхности эллипсоида или шара
(в зависимости от масштаба карт), в косых и поперечных -
только для
поверхности шара (рис.5.2, 6).
Цилиндрические проекции
(cylindrical projection). В
прямых цилиндрических
проекциях параллели и
меридианы изображаются
двумя
семействами параллельных
прямых линий, перпендикулярных
друг другу. Таким образом
задается прямоугольная сетка
цилиндрических проекций
(рис.5.3,а). Промежутки между
параллелями пропорциональны
разностям долгот. Промежутки
между меридианами определяются
принятым характером
изображения или способом
проектирования точек земной
поверхности на боковую
поверхность цилиндра. Из
определения проекций
следует, что их сетка меридианов
и параллелей ортогональна.
Цилиндрические проекции
можно рассматривать как частный
случай конических при а=0
(вершина конуса в
бесконечности) .
По свойствам изображения
проекции могут быть
равноугольными,
равновеликими и произвольными.
Применяются прямые, косые и
поперечные
цилиндрические проекции в
зависимости от расположения
изображаемой области. В косых и
поперечных проекциях
меридианы и па-
а

б
Рис. 5.3. Цилиндрическая проекция:
а - принцип построения проекции;
б - вид проекции

раллели изображаются различными кривыми, но средний меридиан
проекции, на котором располагается полюс косой системы, всегда
прямой.
. Существуют разные способы образования цилиндрических
проекций. Наглядным представляется проектирование земной
поверхности на боковую поверхность цилиндра (рис. S.3, а),
которая затем развертывается на плоскости [2] (рис.5.3, б).
Цилиндр может быть касательным к земному шару или секущим
его. В первом случае длины сохраняются по экватору, во втором -
по двум стандартным параллелям, симметричным относительно
экватора.
Цилиндрические проекции применяются при составлении карт
мелких и крупных масштабов - от общегеографических до
специальных. Так, например, аэронавигационные маршрутные
полетные карты чаще всего составляются в косых и поперечных
цилиндрических равноугольных проекциях (на шаре).
В прямых цилиндрических проекциях одинаково изображаются
одни и те же участки земной поверхности вдоль линии разреза - по
восточной и западной рамкам карты (дублируемые участки карты)
и обеспечивается удобство чтения по широтным поясам (например,
на картах растительности, осадков) или по меридианальным зонам
(например, на картах часовых поясов).
Косые цилиндрические проекции при широте полюса косой
системы, близкой к полярным широтам, имеют географическую
сетку, дающую представление о сферичности земного шара. С
уменьшением широты полюса кривизна параллелей увеличивается,
а их протяжение уменьшается, поэтому уменьшаются и искажения
(эффект сферичности).
В прямых проекциях полюс показывается прямой линией, по
длине, равной экватору, но в некоторых из них (проекции
Меркатора, Уэтча) полюс изобразить невозможно. Полюс
представляется точкой в косых и поперечных проекциях. При
ширине полосы до 4,5° можно использовать касательный цилиндр,
при увеличении ширины полосы следует применять секущий
цилиндр, т.е. вводить редукционный коэффициент.
Поликонические проекции (policonic projection). В них паралле-
ли изображаются дугами эксцентрических окружностей с центрами
на среднем (прямолинейном) меридиане или его продолжении, а
меридианы - кривыми, симметричными относительно среднего
меридиана (рис. 5.4).
Рис. 5.4. Поликоническая проекция
Частным случаем поликонических проекций являются
собственно поликонические проекции, для которых принимаются
дополнительные условия, и круговые проекции с меридианами в
виде дуг эксцентрических окружностей.
К поликоническим проекциям в широком понимании относятся
проекция Таича (определялась аналитически) и проекции
Гинзбурга (получены численными методами).
Видоизмененная простая поликоническая проекция. Она при-
меняется как многогранная. Земная поверхность, принимаемая за
поверхность эллипсоида вращения, делится линиями меридианов и
параллелей на трапеции.
При рассмотрении данной проекции учтем особенности ее
применения при создании карты масштаба 1:1 000 000.
Трапеции изображаются на отдельных листах в одной и той же
проекции (для карты масштаба 1:1 000 000 - в видоизмененной
простой поликонической).
Листы международной карты мира масштаба 1:1 000 000 имеют
определенные размеры сторон трапеций: по меридианам - 4°, по
параллелям - 6°; на широте от 60 до 76° листы сдваивают, они
имеют размеры по параллелям 12°; выше 76° листы счетверяют, их
протяжение по параллелям - 24°.
Применение проекции как многогранной определяет
необходимость введения номенклатура - системы обозначения
отдельных листов.

Для карты масштаба 1:1 000 000 установлено обозначение
трапеций по широтным поясам в направлении от экватора к
полюсам буквами латинского алфавита (А, В, С, D и т.д.) и по
колоннам - арабскими цифрами (1, 2, 3, 4 и т.д.), которые считают
от меридиана с долготой 180° (по Гринвичу) против часовой
стрелки.
Номенклатура сдвоенных и счетверенных листов карты
складывается из обозначений широтного пояса и соответственно
двух или четырех колонн.
Отметим особенности видоизмененной простой
поликонической проекции и распределение искажений в пределах
отдельных листов карты масштаба 1:1 000000.
Меридианы изображаются прямыми линиями. Длина двух
меридианов, отстоящих от среднего на ±2° по долготе (на ±4° на
сдвоенных листах и на ±8° на счетверенных), искажений не имеет.
Крайние параллели каждого листа (северная и южная)
являются дугами окружностей, центры этих параллелей находятся
на среднем меридиане, длина их не искажается.
Для построения внутренних параллелей используют способ
Хинкса, т. е. проводят эти параллели через точки, полученные
путем деления всех меридианов на четыре равные части.
Картографическая сетка строится через 1° по широте и по
долготе, на сдвоенных листах - по долготе через 2°, на
счетверенных - через 4°. Таким образом, все листы карты масштаба
1:1 000 000 имеют пять параллелей и семь меридианов.
Криволинейные меридианы простой поликонической проекции
заменяются в видоизмененной поликонической проекции
прямыми, соединяющими соответствующие точки крайних
параллелей, поэтому масштабы на внутренних параллелях будут
меньше единицы.
Минимальный масштаб получают на средней параллели
каждого листа карты. Для карты масштаба 1 : 1 000 000 искажение
длины средней параллели каждого листа Vn-0,06%.
Масштабы по меридианам и параллелям для этой карты могут
быть приняты за экстремальные (а и b), так как сетка проекции
практически ортогональна. На каждом листе имеются четыре
точки, в которых отсутствуют искажения всех видов; эти точки
находятся на пересечении крайних параллелей листа с
меридианами, удаленными от среднего на 2° к западу и востоку.
Максимальное искажение площади V
р
находится в середине
листа, оно имеет знак минус и может достигать -0,14 %. Изоколы
нулевых искажений
132

площади имеют вид кривых, проходящих через точки, в которых
отсутствуют искажения, и вытянутых вдоль крайних
меридианов.
Достоинством видоизмененной простой поликонической
проекции, применяемой как многогранная, является небольшая
величина искажений. Анализ в пределах листа карты показал,
что искажения длин не превышают 0,10 %, площади -0,15 %,
углов - 5' и являются практически неощутимыми. Недостаток
этой проекции - появление разрывов при соединении листов по
меридианам и параллелям.
Псевдоцилиндрические проекции. В прямых
псевдоцилиндрических проекциях параллели изображаются в
виде прямых параллельных линий, меридианы - в виде кривых
(дуг, синусоид, гипербол, парабол, эллипсов и т.д.) ,
симметричных относительно среднего прямолинейного
меридиана (рис.5.5).
Рис. 5.5. Псевдоцилиндрическая проекция
Промежутки между параллелями определяются принятым
законом изображения земной поверхности на плоскости.
Промежутки между меридианами в равновеликих проекциях
пропорциональны разностям долгот, в других проекциях они
могут убывать или, значительно реже, возрастать от среднего
меридиана к востоку и западу.
Полюс в псевдоцилиндрических проекциях изображается
точкой или полярной линией, длина которой устанавливается
или получается из задания. Поэтому сетка меридианов и
параллелей не ортогональна, в силу чего эти проекции не могут
быть равноугольными.
133

При рассмотрении цилиндрических проекций как частного
случая псевдоцилиндрических проекций, когда меридианы
изображаются прямыми параллельными линиями,
ортогональными к параллелям, цилиндрическую равноугольную
проекцию Меркатора можно считать равноугольной
псевдоцилиндрической проекцией.
Из-за неортогональности сетки экстремальные масштабы не
совпадают с направлением меридианов и параллелей, за
исключением среднего меридиана и экватора.
Псевдоцилиндрические проекции в основном применяются
для изображения всей земной поверхности или значительных ее
частей в мелких масштабах, поэтому земная поверхность
принимается за поверхность шара с радиусом R. Эти проекции
имеют две оси симметрии - экватор и средний меридиан
нормальной сетки. Косые и поперечные псевдоцилиндрические
проекции используются крайне редко.
Проекция Гаусса-Крюгера. К.Ф. Гаусс в 1820 - 1830 гг.
разработал "двойную" равноугольную проекцию, сохраняющую
длины на среднем меридиане. Л.Крюгер в 1912 и 1919 гг.
предложил способ непосредственного отображения эллипсоида
взамен определения, указанного двойной проекцией, и эту
проекцию стали называть проекцией Гаусса-Крюгера (Gauss -
Kruger projection). Она была принята в СССР ( на эллипсоиде
Бесселя) в 1928 г. для всех геодезических и топографических
работ. В ней создавали топографические карты масштабов
крупнее 1:500 000, а с 1939 г. проекция Гаусса-Крюгера стала
применяться и для карты масштаба 1:500 000.
В апреле 1946 г. постановлением правительства были
утверждены размеры референц-эллипсоида Красовского и
новые исходные даты, характеризующие систему координат
1942 г.
Проекция Гаусса-Крюгера не является строго
равноугольной, так как при ее получении использовано
разложение в такой ряд, для которого выполняется только одно
из условий Коши-Римана.
При введении в уравнение проекции еще одного
дополнительного члена ряда начинает выполняться второе
условие, а первое, которое сохранялось ранее, не выполняется.
Проекция при сохранении в ее формулах достаточного
количества (7-8) членов является практически равноугольной,
поэтому можно считать, что в ней соблюдаются условия
ортогональности сетки и равенства масштабов.
В проекции Гаусса-Крюгера поверхность эллипсоида на
плоскости отображается по меридианным зонам, ширина
которых равна 6° (для
