Curry G.L., Feldman R.M. Manufacturing Systems Modeling and Analysis

Подождите немного. Документ загружается.

1.4 Important Distributions 23

with mean

and variance

. (Notice that the name arrises because the random

variable deﬁned by the natural log of Y ; namely ln(Y ), is normally distributed.) This

distribution is always non-negative and can have a relatively large right-hand tail.

It is often used for modeling repair times and also for modeling many biological

characteristics. It is not difﬁcult to obtain the mean and variance of the log-normal

distribution from the characteristics of the normal:

= e

, and

×(e

−1) . (1.22)

Because t he distribution is skewed to the right (long right-hand tail), the mean is

to the right of the mode which is given by e

−

. If the mean and variance of the

log-normal distribution is known, it is straight forward to obtain the characteristics

of the normal random variable that generates the log-normal, speciﬁcally

= ln(c

+ 1 ) , and

= ln(

) −

, (1.23)

where the squared coefﬁcient of variation is given by c

Skewness: Before moving to the discussion of more than one random variable,

we mention an additional descriptor of distributions. The ﬁrst moment gives the

central tendency for random variables, and the second moment is used to measure

variability. The third moment, that was not discussed previously, is useful as a mea-

sure of skewness (i.e., non-symmetry). Speciﬁcally, the coefﬁcient of skewness,

for a random variable T with mean

and standard deviation

is deﬁned by

E[(T −

)

]

, (1.24)

and the relation to the other moments is

E[(T −

)

]=E[T

] −3

E[ T

]+2

A symmetric distribution has

= 0; if the mean is to the left of the mode,

< 0

and the left-hand side of the distribution will have the longer tail; if the mean is to

the right of the mode,

> 0 and the right-hand side of the distribution will have

the longer tail. For example,

= 0 for the normal distribution,

= 2fortheex-

ponential distribution,

= 2/

√

k for a type-k Erlang distribution, and for a gamma

distribution, we have

= 2/

√

. The Weibull pdf’s shown in Fig. 1.12 have skew-

ness coefﬁcients of 3.9 and 0.63, respectively, for the solid line ﬁgure and dashed

line graphs. Thus, the value of

can help complete the intuitive understanding of a

particular distribution.

• Suggestion: Do Problems 1.15–1.19.

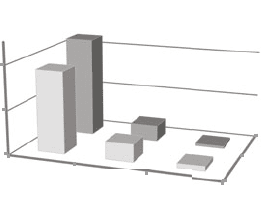
24 1 Basic Probability Review

Fig. 1.14 Probability mass

function for the two discrete

random variables from Exam-

ple 1.12

R=0

R=1

0.2

0.4

N=0

N=1

N=2

1.5 Multivariate Distributions

The analysis of physical phenomena usually involves many distinct random vari-

ables. In this section we discuss the concepts involved when two random variables

are deﬁned. The extension to more than two i s left to the imagination of the reader

and the numerous textbooks that have been written on the subject.

Deﬁnition 1.12. The function F is called the joint cumulative distribution function

for X

and X

F(a,b)=Pr{X

≤ a, X

≤ b}

for a and b any two real numbers.

In a probability statement as in the right-hand-side of the above equation, the

comma means intersection of events and is read as “The probability that X

is less

than or equal to a and X

is less than or equal to b”. The initial understanding of

joint probabilities is easiest with discrete random variables.

Deﬁnition 1.13. The function f is a joint pmf for the discrete random variables X

and X

f (a,b)=Pr{X

= a, X

= b}

for each (a, b) in the range of (X

For the single-variable pmf, the height of the pmf at a speciﬁc value gives the

probability that the random variable will equal that value. It is the same for the

joint pmf except that the graph is in three-dimensions. Thus, the height of the pmf

evaluated at a speciﬁed ordered pair gives the probability that the random variables

will equal those speciﬁed values (Fig. 1.14).

It is sometimes necessary to obtain from the joint pmf the probability of one

random variable without regard to the value of the second random variable.

1.5 Multivariate Distributions 25

Deﬁnition 1.14. The marginal pmf for X

and X

, denoted by f

and f

, respec-

tively, are

(a)=Pr{X

= a} =

∑

f (a,k)

for a in the range of X

, and

(b)=Pr{X

= b} =

∑

f (k,b)

for b in the range of X

Example 1.12. We return again to Example 1.1 to illustrate these concepts. The ran-

dom variable R will indicate whether a randomly chosen box contains radio phones

or plain phones; namely, if the box contains radio phones then we set R = 1 and

if plain phones then R = 0. Also the random variable N will denote the number of

defective phones in the box. Thus, according to the probabilities deﬁned in Exam-

ple 1.1, the joint pmf,

f (a, b)=Pr{R = a,N = b} ,

has the probabilities as listed in Table 1.1. By summing in the “margins”, we obtain

Table 1.1 Joint probability mass function of Example 1.12

N = 0 N = 1 N = 2

R = 0 0.37 0.08 0.02

R = 1 0.45 0.07 0.01

the marginal pmf for R and N separately as shown in Table 1.2. Thus we see, for

Table 1.2 Marginal probability mass functions of Example 1.12

N = 0 N = 1 N = 2 f

(·)

R = 0 0.37 0.08 0.02 0.47

R = 1 0.45 0.07 0.01 0.53

(·) 0.82 0.15 0.03

example, that the probability of choosing a box with radio phones (i.e., Pr{R = 1})is

53%, the probability of choosing a box of radio phones that has one defective phone

(i.e., Pr{R = 1,N = 1}) is 7%, and the probability that both phones in a randomly

chosen box (i.e., Pr{N = 2}) are defective is 3%. 

Continuous random variables are treated in an analogous manner to the discrete

case. The major difference in moving from one continuous random variable to two

is that probabilities are given i n terms of a volume under a surface instead of an area

under a curve (see Fig. 1.15 for representation of a joint pdf).

Deﬁnition 1.15. The functions g, g

, and g

are the joint pdf for X

and X

,the

marginal pdf for X

, and the marginal pdf for X

, respectively, as the following

26 1 Basic Probability Review

Fig. 1.15 Probability density

function for the two contin-

uous random variables from

Example 1.13

y=0

y=0.5

y=1

0.0

1.0

2.0

3.0

x=0

x=0.5

x=1

hold:

Pr{a

≤ X

≤ b

≤ X

≤ b

} =



g(s

)ds

(a)=



∞

−∞

g(a,s)ds

(b)=



∞

−∞

g(s,b)ds ,

where

Pr{a ≤ X

≤ b} =



(s)ds

Pr{a ≤ X

≤ b} =



(s)ds .

We return now to the concept of conditional probabilities (Deﬁnition 1.3). The

situation often arises in which the experimentalist has knowledge regarding one

random variable and would like to use that knowledge in predicting the value of the

other (unknown) random variable. Such predictions are possible through conditional

probability functions

Deﬁnition 1.16. Let f be a joint pmf for the discrete random variables X

and X

with f

the marginal pmf for X

. Then the conditional pmf for X

given that X

= b

is deﬁned, if Pr{X

= b} = 0, to be

1|b

(a)=

f (a, b)

(b)

where

Pr{X

= a|X

= b} = f

1|b

(a) .

1.5 Multivariate Distributions 27

Deﬁnition 1.17. Let g be a joint pdf for continuous random variables X

and X

with g

the marginal pdf for X

. Then the conditional pdf for X

given that X

= b

is deﬁned to be

1|b

(a)=

g(a,b)

(b)

where

Pr{a

≤ X

≤ a

= b} =



1|b

(s)ds .

The conditional statements for X

givenavalueforX

are made similarly to

Deﬁnitions 1.16 and 1.17 with the subscripts reversed. These conditional statements

can be illustrated by using Example 1.12. It has already been determined that the

probability of having a box full of defective phones is 3%; however, let us assume

that it is already known that we have picked a box of radio phones. Now, given a

box of radio phones, the probability of both phones being defective is

2|a=1

(2)=

f (1,2)

(1)

0.01

0.53

= 0.0189 ;

thus, knowledge that the box consisted of radio phones enabled a more accurate

prediction of the probabilities that both phones were defective. Or to consider a

different situation, assume that we know the box has both phones defective. The

probability that the box contains plain phones is

1|b=2

(0)=

f (0,2)

(2)

0.02

0.03

= 0.6667 .

Example 1.13. Let X and Y be two continuous random variables with joint pdf given

f (x,y)=

+ y) for 0 ≤ x ≤1, 0 ≤ y ≤1 .

Utilizing Deﬁnition 1.15, we obtain

(x)=

+ 0.5) for 0 ≤ x ≤1

(y)=

(y + 0.25) for 0 ≤ y ≤ 1 .

To ﬁnd the probability that Y is less than or equal to 0.5, we perform the following

steps:

Pr{Y ≤ 0.5} =



0.5

(y)dy



0.5

(y + 0.25)dy =

28 1 Basic Probability Review

To ﬁnd the probability that Y is less than or equal to 0.5 given we know that X = 0.1,

we perform

Pr{Y ≤ 0.5|X = 0.1} =



0.5

2|0.1

(y)dy



0.5

0.1

+ y

0.1

+ 0.5

0.1255

0.501

≈



Example 1.14. Let U and V be two continuous random variables with joint pdf given

g(u,v)=8u

v for 0 ≤ u ≤ 1,0 ≤ v ≤ 1 .

The marginal pdf’s are

(u)=4u

for 0 ≤ u ≤ 1

(v)=2v for 0 ≤ v ≤ 1 .

The following two statements are easily veriﬁed.

Pr{0.1 ≤V ≤ 0.5} =



0.5

0.1

2vdv = 0.24

Pr{0.1 ≤V ≤ 0.5|U = 0.1} = 0.24 .



The above example illustrates independence. Notice in the example that knowl-

edge of the value of U did not change the probabilities regarding the probability

statement of V .

Deﬁnition 1.18. Let f be the joint probability distribution (pmf if discrete and pdf

if continuous) of two random variables X

and X

. Furthermore, let f

and f

be the

marginals for X

and X

, r espectively. If

f (a,b)= f

(a) f

(b)

for all a and b, then X

and X

are called independent.

Independent random variables are much easier to work with because of their

separability. However, in the use of the above deﬁnition, it is important to test the

property for all values of a and b. It would be easy to make a mistake by stopping

after the equality was shown to hold for only one particular pair of a,b values. Once

independence has been shown, the following property is very useful.

1.5 Multivariate Distributions 29

Property 1.6. Let X

and X

be independent random variables. Then

E[X

]=E[X

]E[X

]

and

V [X

+ X

]=V [X

]+V [X

] .

Example 1.15. Consider again the random variables R and N deﬁned in Example

1.12. We see from the marginal pmf’s given in that example that E[R]=0.53 and

E[N]=0.21. We also have

E[R ·N]=0 ×0 ×0 .37 + 0 ×1 ×0.08 + 0 ×2 ×0.02

+ 1 ×0 ×0.45 + 1 ×1 ×0.07 + 1 ×2 ×0.01 = 0.09 .

Thus, it is possible to say that the random variables R and N are not independent

since 0.53 ×0.21 = 0.09. If, however, the expected value of the product of two

random variables equals the product of the two individual expected values, the claim

of independence is not proven. 

We close this section by giving two ﬁnal measures that are used to express the

relationship between two dependent random variables. The ﬁrst measure is called

the covariance and the second measure i s called the correlation coefﬁcient.

Deﬁnition 1.19. The covariance of two random variables, X

and X

, is deﬁned by

cov(X

)=E[(X

−E[X

])(X

−E[X

])] .

Property 1.7. The following is often helpful as a computational aid:

cov(X

)=E[X

] −

where

and

are the means for X

and X

, respectively.

Comparing Property 1.6 to Property 1.7, it should be clear that random variables

that are independent have zero covariance. However, it is possible to obtain random

variables with zero covariance that are not independent. (See Example 1.17 below.)

A principle use of the covariance is in the deﬁnition of the correlation coefﬁcient,

that is a measure of the linear relationship between two random variables.

Deﬁnition 1.20. Let X

be a random variable with mean

and variance

.LetX

be a r andom variable with mean

and variance

.Thecorrelation coefﬁcient ,

denoted by

,ofX

and X

is deﬁned by

30 1 Basic Probability Review

cov(X

)



V (X

)V (X

)

E[ X

] −

The correlation coefﬁcient is always between negative one and positive one. A

negative correlation coefﬁcient indicates that if one random variable happens to be

large, the other random variable is likely to be small. A positive correlation coef-

ﬁcient indicates that if one random variable happens to be large, the other random

variable is also likely to be large. The following examples illustrate this concept.

Example 1.16. Let X

and X

denote two discrete random variables, where X

ranges

from 1 to 3 and X

ranges from 10 to 30. Their joint and marginal pmf’s are given

in Table 1.3.

Table 1.3 Marginal probability mass functions of Example 1.16

= 10 X

= 20 X

= 30 f

(·)

= 1 0.28 0.08 0.04 0.4

= 2 0.04 0.12 0.04 0.2

= 3 0.04 0.08 0.28 0.4

(·) 0.36 0.28 0.36

The following facts should not be difﬁcult to verify:

= 2.0,

= 0.8,

20.0,

= 72.0, and E[X

]=44.8. Therefore the correlation coefﬁcient of X

and

is given by

44.8 −2 ×20

√

0.8 ×72

= 0.632 .

The conditional probabilities will help verify the intuitive concept of a positive cor-

relation coefﬁcient. Figure 1.16 contains a graph illustrating the conditional prob-

abilities of X

given various values of X

; the area of each circle in the ﬁgure is

proportional to the conditional probability. Thus, the ﬁgure gives a visual represen-

tation that as X

increases, i t is likely (but not necessary) that X

will increase. For

example, the top right-hand circle represents Pr{X

= 30|X

= 3} = 0.7, and the

middle right-hand circle represents Pr{X

= 20|X

= 3} = 0.2.

As a ﬁnal example, we switch the top and middle right-hand circles in Fig. 1.16

so that the appearance is not so clearly linear. (That is, let Pr{X

= 3, X

= 20} =

0.28, Pr{X

= 3,X

= 30} = 0.08, and all other probabilities the same.) With this

change,

and

remain unchanged,

= 18,

= 48 .0, cov(X

)=2.8 and

the correlation coefﬁcient is

= 0.452. Thus, as the linear relationship between X

and X

weakens, the value of

becomes smaller. 

If the random variables X and Y have a linear relationship (however “fuzzy”),

their correlation coefﬁcient will be non-zero. Intuitively, the square of the corre-

lation coefﬁcient,

, i ndicates that amount of variability that is due to that linear

relationship. For example, suppose that the correlation between X and Y is 0.8 so

that

= 0.64. Then 64% of the variability in Y is due the variability of X through

their linear relationship.

1.5 Multivariate Distributions 31

Fig. 1.16 Graphical rep-

resentation for conditional

probabilities of X

given X

from Example 1.16,where

the correlation coefﬁcient is

0.632

Fig. 1.17 Graphical rep-

resentation for conditional

probabilities of X

given X

from Example 1.17,wherethe

correlation coefﬁcient is zero

123

Example 1.17. Let X

and X

denote two discrete random variables, where X

ranges

from 1 to 3 and X

ranges from 10 to 30. Their joint and marginal pmf’s are given

in Table 1.4.

Table 1.4 Marginal probability mass functions of Example 1.17

= 10 X

= 20 X

= 30 f

(·)

= 1 0.28 0.08 0.04 0.4

= 2 0.00 0.02 0.18 0.2

= 3 0.28 0.08 0.04 0.4

(·) 0.56 0.18 0.26

Again, we give the various measures and allow the reader to verify their accuracy:

= 2,

= 17, and E[X

]=34. Therefore the correlation coefﬁcient of X

and

is zero so there is no linear relation between X

and X

; however, the two random

variables are clearly dependent. If X

is either one or three, then the most likely value

of X

is 10; whereas, if X

is 2, then it is impossible for X

to have the value of 10;

thus, the random variables must be dependent. If you observe the representation of

the conditional probabilities in Fig. 1.17, then the lack of a linear relationship is

obvious. 

• Suggestion: Do Problems 1.21–1.26.

32 1 Basic Probability Review

1.6 Combinations of Random Variables

This probability review is concluded with a discussion of a problem type that will be

frequently encountered in the next several chapters; namely, combinations of ran-

dom variables. The properties of the sum of a ﬁxed number of random variables is

a straightforward generalization of previous material; however when the sum has a

random number of terms, an additional variability factor must be taken into account.

The ﬁnal combination discussed in this section is called a mixture of random vari-

ables. An example of a mixture is the situation where the random processing time

at a machine will be from different probability distributions based on the (random)

product type being processed. Each of these three combinations of random variables

are considered in turn.

1.6.1 Fixed Sum of Random Variables

Consider a collection of n random variables, X

,··· ,X

and let their sum be

denoted by S; namely,

S =

∑

i=1

. (1.25)

By a generalization of Property 1.3,wehave

E[ S]=E[X

+ X

+ ···+ X

]

= E[X

]+E[X

]+···+ E[X

] . (1.26)

Note that (1.26) is valid even if the random variables are not independent.

The variance of the random variable S is obtained in a similar manner to the

expected value

V [S]=E[(S −E[S])

]

= E[S

] −E[S ]

= E[(X

+ X

+ ···+ X

)

] −(E[ X

]+E[X

]+···+E[X

])

∑

i=1

E[X

]+2

∑

i=1

∑

j>i

E[ X

] −(E[X

]+E[X

]+···+ E[X

])

∑

i=1



E[ X

] −E[X

]



+ 2

∑

i=1

∑

j >i

(E[X

] −E[X

]E[X

])

∑

i=1

V [X

]+2

∑

i=1

∑

j>i

cov[X

] . (1.27)