Crank J. Free and Moving Boundary Problems

342

Numerical solution

of

free-boundary problems

by

{x}o

and

the

process is halted when

I{X}o+1_{X}ol~B,

for some pre-

scribed accuracy

B.

The solutions

{x}o+1

and

y~

do

not sati'lfy

the

remain-

ing equation

fn+1(X1,

X2,

...

,Xn,

Yc)

= 0

and depending on the sign of

fn+1({X}0+1,

y~),

y~

i'l

increased

or

decreased

to

give a new trial value y

~

for the next stage of the iteration cycle, which

continues until successive iterates differ by

les.'I

than a prescribed amount.

The initial trial value

y~

was taken

to

be

!(H

+ h).

In order

to

facilitate completely automatic me'lh generation, Finn and

VarogIu (1977) started from a rectangular me'lh of constant

4>

and

constant

y lines in a rectangular

4>,

y domain (Fig. 8.7) where a nodal

point

(~,

yJ

is

given by

~

=

(I

-

Yc)/(Yc

-

H),

=

(</>;

- yc)/(h -

H),

YI

=

yJI'

Yc

~</>;

~H,

h

~</>;

~yc'

(8.57)

(8.58)

To

each node

(~,

Yi)

in the

4>,

y plane there corre'lponds a node

(</>;,

yJ

in

the

x,

y plane depending on

the

unknowns

Yc

and

x;.

An

initial set of trial

values of

x coordinate value'l associated with the

(<1>1,

yJ

values is also

needed

to

start the iterative solution. These x values are arbitrary except

that they must preserve

the

sequential ordering of equipotential lines, i.e.

if

<1>1>

<1>2

>

<1>3,

the

trial x values cannot

be

such as

to

put

<1>3

between

<1>1

and

<1>2'

Finn and Varoglu (1977) de'lcribed one satisfactory procedure.

They took

the

free surface initially

to

be

the straight line BC.

The

equipotential line

=

y~

is

assumed to be the line

CF

which is normal

to

BC and intersects the base

AE

in F (Fig. 8.8a). All other equipoten-

tialline'l were assumed

to

be

straight initially and were located as follows.

The

equipotential line

= constant corre'lponding

to

a specific line

4>

=

constant is taken to intersect

the

free surface BC

or

the seepage face

CD

in a point at which y =

<1>.

The

other

end of the assumed straight line

= constant

is

at G on AF, where

(H

-

)/(<1>

-

y~)

= AG/GF. A similar

jl

1.0

-1.0

1.0

FIG. 8.7. Mesh for numerical examples

in

the

,"b-y

plane

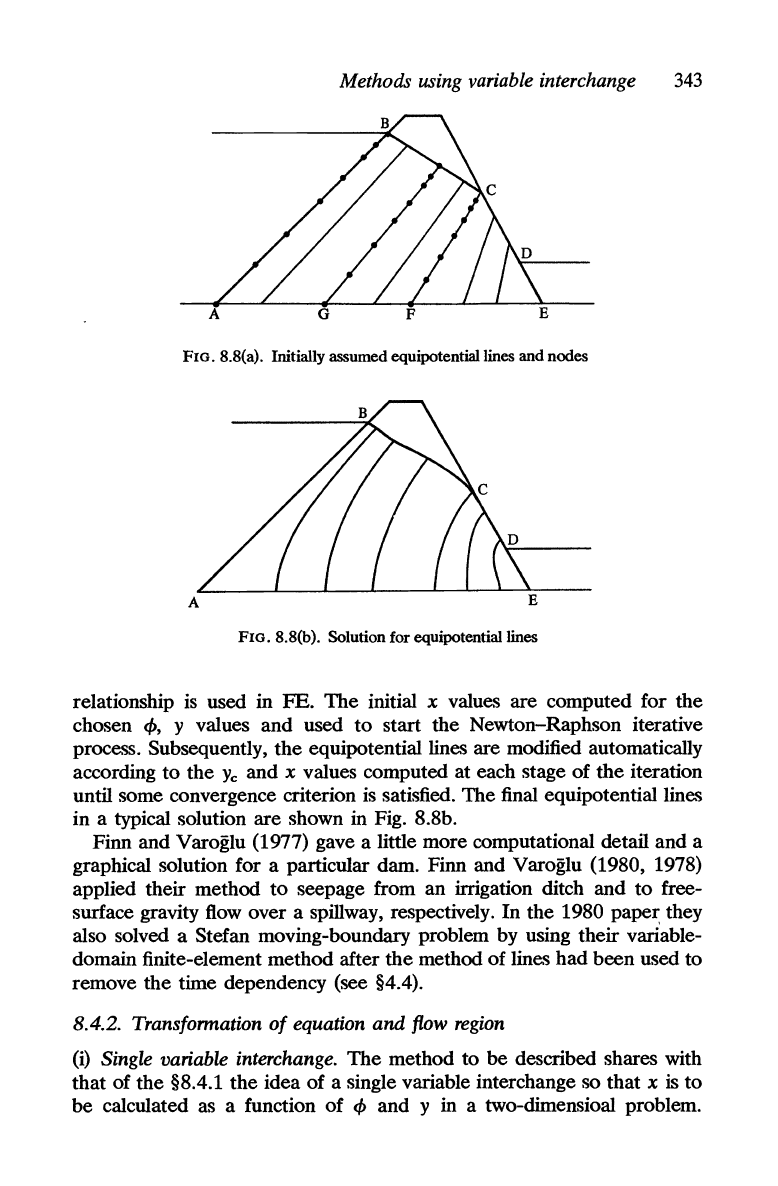
Methods using variable interchange

343

A

FIG. 8.8(a). Initially assumed equipotential lines and nodes

A

E

FIG. 8.8(b). Solution for equipotential lines

relationship

is

used in

FE.

The

initial x values are computed for the

chosen

q"

y values and used

to

start the Newton-Raphson iterative

process. Subsequently,

the

equipotential lines are modified automatically

according

to

the

Yc

and x values computed at each stage of

the

iteration

until some convergence criterion

is

satisfied. The final equipotential lines

in a typical solution are shown in Fig. 8.8b.

Finn and Varoglu (1977) gave a little more computational detail and a

graphical solution for a particular dam. Finn and Varoglu (1980, 1978)

applied their method

to

seepage from an irrigation ditch and

to

free-

surface gravity flow over a spillway, respectively. In the 1980 paper they

also solved a Stefan moving-boundary problem by using their varlable-

domain finite-element method after

the

method of line'! had been used to

remove

the

time dependency (see §4.4).

8.4.2. Transformation

of

equation

and

flow region

(i)

Single variable interchange. The method to be described shares with

that of the §8.4.1

the

idea of a single variable interchange so that x is

to

be calculated as a function

of

q,

and y in a two-dimensioal problem.

344

Numerical solution

of

free-boundary problems

Crank and Ozis (1980), however, transformed the elliptic equation and

solved

the

new equation for x = x(q" y) subject

to

appropriately rewritten

conditions

on

the

boundaries of a fixed domain in the

q"

y plane which is

a transformation

of

the

flow

region in the

x,

y plane.

The

idea is well trie4

in fluid-flow problems and has been applied to moving boundary prob-

lems under the name Isotherm Migration Method (IMM) as described in

§5.4.

The

need to determine the position

of

the whole

of

the free

boundary in

the

physical plane is reduced to locating the position of

the

separation point

on

a fixed, straight-line boundary in

the

transformed

plane.

An

iterative algorithm approximates within each single loop both a

finite-difference solution

of

the elliptic partial differential equation and

the position

of

the

free boundary.

The simple

dam

problem

of

Fig. 2.1 and equations (2.7-12) are used as

an example. Crank and Ozis (1980) transformed

the

appropriate form

of

(2.7), i.e.

into

aZq,

_

aZx

(ax)-3

=0

ayZ

aq,z

aq,

(8.59)

(8.60)

by changing

the

variables only in

the

first

term

of (8.59). They then

treated the

;Pq,/ayz

term in (8.60) by

an

interpolation procedure.

Later

work by Crank

and

Sabouri, reported by Ozis (1981), showed that both

accuracy and convergence were improved by a complete transformation

of

(8.59) following Boadway's (1976) treatment

of

fluid-flow problems

presented in

§5.4.2(ii). With suitable change

of

nomenclature and by

putting

az/at

= 0,

the

fully transformed form

of

(8.59) follows immediately

from the two-dimensional version

of

(5.76) and is

aZx

(ax)Z +

aZx

{1 +

(ax)Z}

_ 2

aZx

ax

=

O.

(8.61)

ayZ

aq,

aq,z

ay

aq,

ay

aq,

Apart from the differences in the finite-difference discretizations

of

(8.60) and (8.61), Crank and Sabouri used

the

same algorithm as

that

of

Crank and Ozis (1980).

In

general,

on

a boundary y = g(x) we have

g'<bx-~

q,n

= [1 +

(g')Z,

' g' = dy/dx, (8.62)

where, for example,

<bn

=

aq,/an

and n is

the

outward normal

to

y = g(x).

Provided

g'=j=O,

we have

on

the free boundary

PD,

in Fig. 2.1,

g'

aq,/ax-aq,/ay

=0,

y =

q,.

(8.63)

But

(aq,/aY)x=-(ax/ay)/(ax/a</J)

and

(aq,/ax)y=l/(ax/aq,)y

so that

g' +

(ax/aY)

= 0, y =

q,.

(8.64)

Methods using variable interchange

345

It

is

true

that g' =

00

at the separation point D but condition (8.64)

is

not

applied

at

that point.

On

the impervious base

AB

we have

aX/ay

=0,

y=O.

(8.65)

The

other boundary conditions are

x=O,

</>

= 1

onAF,

X=Xh

</>

=

Y2'

0~Y~Y2

onBC,

(8.66)

X=Xh

</>=y

on CD.

(8.67)

We

now wish

to

solve (8.61)

or

(8.60), subject

to

conditions (8.64-67)

in

the

region

A'FD'CB'

in Fig. 8.9 in the

</>,

y plane. All the boundaries

are fixed.

The

original free boundary

FD

has become the known straight

boundary,

FD',

y =

</>.

What we do not know, however, is the position of

D'

on

FC

corresponding

to

the separation point D in Fig. 2.1, at which

the

boundary condition changes from x = Xl

to

the

condition (8.64).

The

transformed region in Fig. 8.9

is

covered with a

meo;h

of spacings

8</>,

8y

and X;j

denote.o;

x(i8</>,

j8y).

For a typical internal node

i,

j the

Jacobi-type iterative process

wao;

used

to

solve (8.61)

in

the form

4[(X~I,j-

xr-l,j?+4(8y)2+

(x~j+1

-

XY_I)2]x~r

= [2(XY+I +

XY-I)(X~I,j-

Xr-l,j?+

2(X~+I,j+

X~-IJ)

x {4(8y)2 +

(X~j+l

-

X~j-I?}-{(X~+1J+I

- Xr-IJ+I)

-

(X~+1,j-1

-

Xr-I,j-I)}(X~j+1

-

X~j-I)(X~I,j-

Xr-l,j)],

(8.68)

where

X~j

is

the

nth

iterative value of X;J. Correspondingly,

on

the bound-

ary

FC,

y =

</>

we use either X = Xl

or

n+l_

n 2(8y)2

Xj,j

- Xj,j-l - n n

Xj+l,/+l -

Xj-IJ-I

from (8.64), where a one-sided difference replacement of

(iJx/iJY)<t>

is

used

FIG. 8.9. Transfonned plane

346

Numerical solution

of

free-boundary problems

to

avoid fictitious points outside

the

region. Application

of

(8.68)

to

points

on

the lower boundary y = 0, i.e. j = 0, introduces ficitious points

on

the line j =

-1,

one

step outside

the

region; these can

be

eliminated

from (8.68) since (8.65) implies

Xi,-l =

Xi,l

for all

i.

The

iteration can

be

started by assuming

the

separation point

D'

to

be

at one of

the

mesh points

on

FC

in Fig. 8.9.

It

follows that x =

Xl

along

B'C

and C'D', and we know

that

X = 0

on

A'F.

For

every

other

mesh

point within the region and

on

the

remaining parts

of

the boundary we

have derived an equation. We can carry

out

one

iterative cycle

by

sweeping along successive j-lines from left

to

right in Fig. 8.9 in

the

order

j =

0,1,2,

...

, where y = j = 0

is

the

lower boundary.

The

new values of

Xij

are retained for use in the next cycle subject

to

the

proviso

that

on

the

boundary

FC

we take

the

new value

x~tl

to

be

since we know

Xi.i

:S;;Xl'

We

proceed with successive iterative loops,

improving

the

solution, which through

the

Xi,i

values

on

FC

includes

the

position of

the

free boundary and

the

position of

the

separation point,

until some prescribed convergence criterion is satisfied.

In

the

absence of

any prior knowledge of the position of

D',

the

iterative process can

be

started by assuming

D'

to

be

at

C,

its lowest possible position. This

ensures

that

D'

is

always approached from below its true position in

the

iterative cycle.

The

initial values

of

x along

FD'

were taken by

Crank

and

Ozis (1980)

to

be

linear interpolates between x = 0

at

F and x =

Xl

at

D'.

On

each line y = constant they

took

linear interpolates between

the

end

values

on

B'CD'

and

NF

for

the

initial values of x

at

internal mesh

points.

Ozis (1981) reported an improved

rate

of iterative convergence by

starting from parabolic interpolated values

of

x

both

along

FD'

and

inside the domain.

The

parabolic form allows certain physical properties

to

be

taken into account. Thus along

the

free surlace

FD',

iJrJ>/ax

= 0

at

F

and this can

be

incorporated in a parabolic expression for

the

x-values

along

FD'

which fits x = 0

at

F,

x =

Xl

at

D'.

A similar set of parabolic

interpolates for initial x-values along any mesh line of constant

y can

be

obtained which has

arJ>/ax

= 0 along

A'F

and

which has x =

Xl

along

B'CD'

and x has

the

interpolated initial values along

FD'

just obtained.

For

the particular

dam

used by various

other

authors in which

Xl

= 2/3,

Y2

= 1/6 relative

to

a water depth of unity

on

the

inlet side, Table 8.3

compares values

of

10

4

x

at

chosen values

of

y

on

the free boundary,

obtained by solving (8.61) for two mesh sizes

h = 1/18 and h = 1/30 with

values computed from the analytical solution of Polubarinova-Kochina

(1962).

Other

solutions and comparisons are

to

be

found in

Crank

and

Ozis (1980) and Ozis (1981).

Crank and Ozis (1980) described

the

use

of

a 'parabolic tail' in an

attempt

to

improve

the

position of

the

estimated separation point by

Methods using variable interchange

347

TABLE

S.3

Comparison

of

free-boundary position

by variable interchange with analytic

solution

10

4

X

104y

h=

1/18

h=1/30

Analytic

5284

6667

6667 6667

5333

6667

6652

5667

6667

6508

6467

6000

6251

6213

6231

6333

5966

5942 5957

6667

5695

5618

5651

7000

5326 5276

5311

7333

4950

4901 4940

7667 4560

4497

4535

8000

4118 4059

4093

8333

3651

3582

3611

8667 3107

3061

3083

9000

2523

2484

2498

9333

1853

1831

1829

9667

1061

1067

ensuring that the gradient

of

the free boundary, dx/dy, should approach

zero

at

D'. H an accurate solution is required near D', however, Aitchi-

son's singularity solution given

in

equation (S.35) above needs

to

be

incorporated.

Crank and

Ozis (19S1) extended their variable-interchange method to

a model three-dimensional problem, which was

the

seepage of fluid

through a circular porous dam. Although the problem had circular

symmetry Crank and Ozis ignored this and treated it as a general

three-dimensional problem in three cartesian space variables,

x,

y,

z.

Afterwards, and quite independently, they solved the two-dimensional

problem reformulated in the

r-z

plane in order to compare the two

results.

The

mathematical formulation

of

the problem illustrated in Fig. S.10

is

as follows:

V

2

ef>

=

cief>

+

cief>

+

cief>

= 0 in AEDCLMFG,

iJx

2

iJy2

iJz2

ef>

=H

on AEFG,

iJcf>/iJn

= 0

on

EDMF,

ef>

= h on DMPN,

ef>

= y

On

CNPL, the seepage surface,

iJef>/dn

= 0 on

ABDE

and GFMK,

ef>

=

y,

iJef>/iJn

= 0

on

ACLG, the free surface,

where n

is

the outward normal.

(S.69a)

(S.69b)

(S.69c)

(S.69d)

(S.6ge)

(S.69f)

(S.69g)

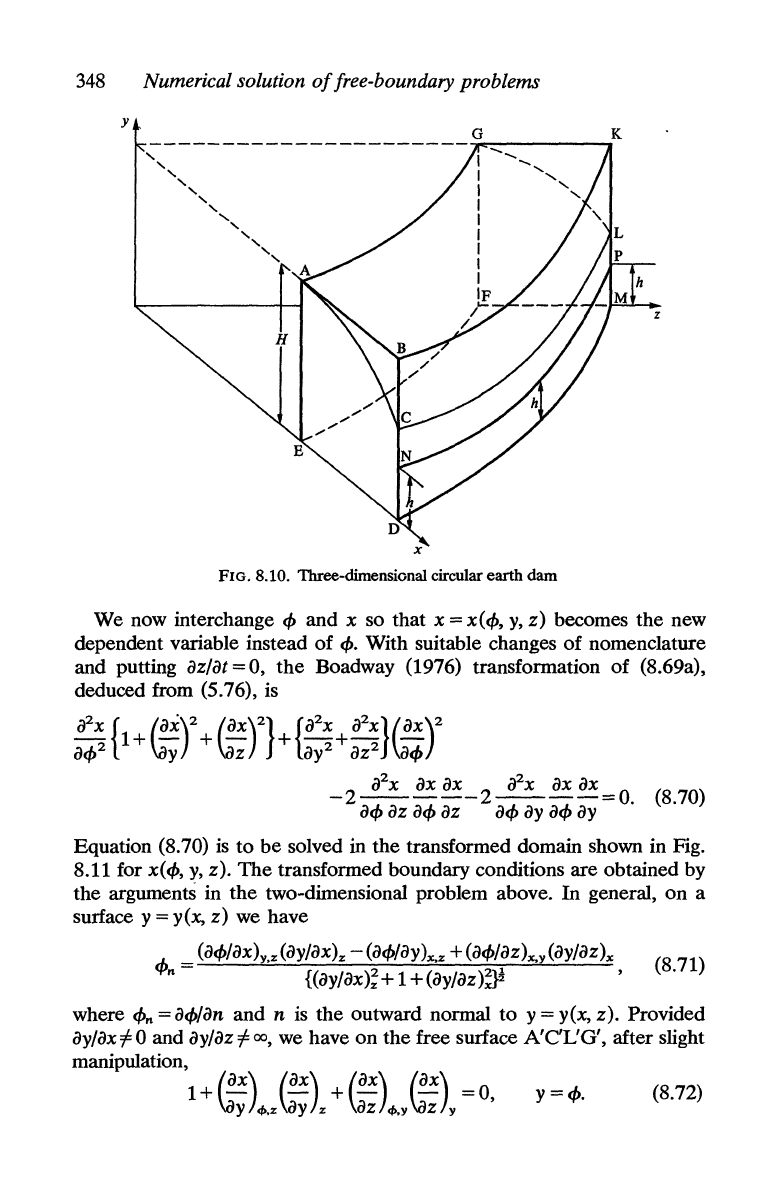
348

Numerical solution

of

free-boundary problems

y

x

FIG. 8.10. Three-dimensional circular earth dam

We

now interchange

q,

and

x so

that

x = x(q"

y,

z)

becomes

the

new

dependent variable instead

of

q,.

With suitable changes

of

nomenclature

and putting

iJz/iJt

= 0,

the

Boadway (1976) transformation

of

(8.69a),

deduced from (5.76), is

iJ

2

x

{1

+

{~i)2

+ (iJX)2}+ {iJ

2

X +

iJ

2

x}

(iJX)2

iJq,2

\ay

\az

iJy2

iJ

z

2

iJq,

_ 2

iJ

2

x

iJx iJx

_ 2

iJ

2

x

iJx iJx

=

O.

iJq,

iJz

iJq,

iJz

iJq,

iJy

iJq,

iJy

(8.70)

Equation (8.70) is

to

be

solved in

the

transformed domain shown

in

Fig.

8.11 for x(q"

y,

z).

The

transformed boundary conditions

are

obtained by

the

argumentS in

the

two-dimensional problem above.

In

general,

on

a

surface y = y(x,

z)

we have

q,

= (iJq,/iJx\'z(iJy/iJx)z -(iJq,/iJy)x.z +

(iJq,/iJz)x,y(iJy/iJz)x

(8.71)

n {(iJy/iJx);+ 1

+(iJy/iJz)~

,

where

q,n

=

iJq,/iJn

and

n is

the

outward normal

to

y = y(x, z). Provided

iJy/iJxf=O

and

iJy/iJzf=oo,

we have

on

the

free surface A'C'L'G', after slight

manipulation,

1 + (iJX) (iJX) + (iJX) (iJX) = 0 Y =

q,.

(8.72)

\ay

.z

iJy

z

iJz

.y

\az

y ,

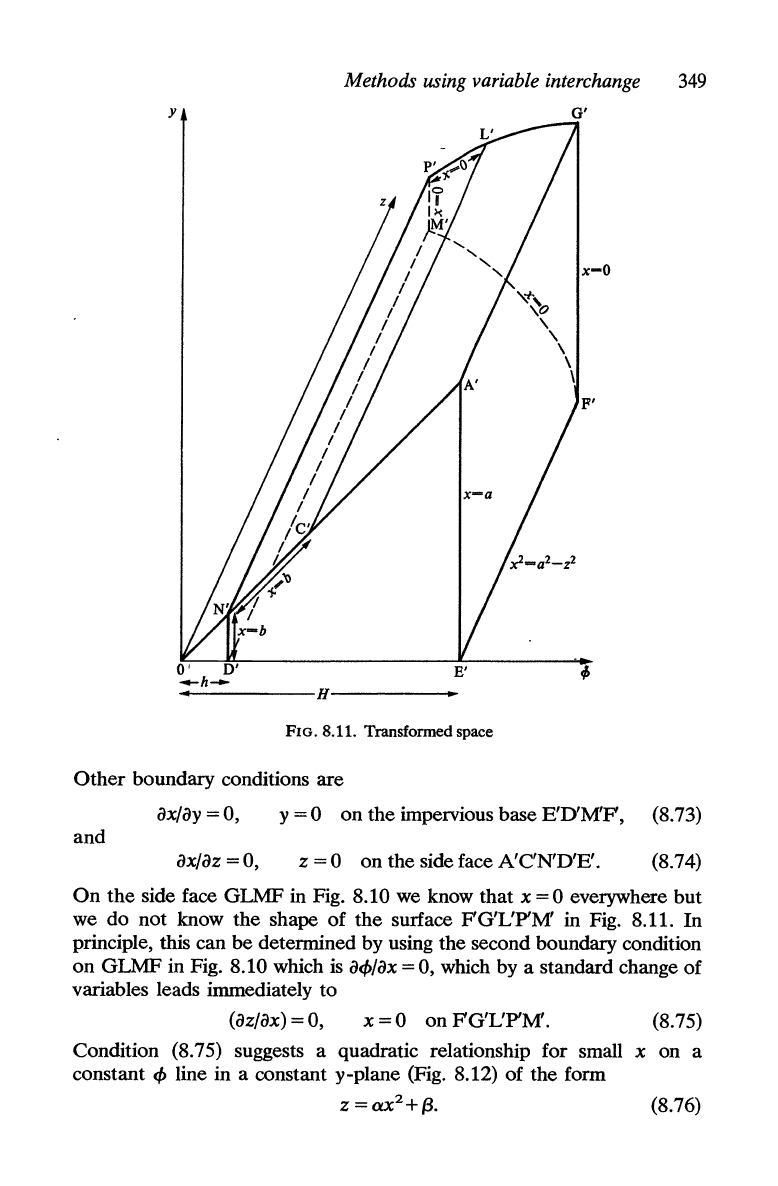
Methods using variable interchange

349

y

G'

~----------H----------·

FIG. 8.11. Transfonned space

Other

boundary conditions are

ax/ay

=0,

y

=0

on

the impervious base

E'D'M'P,

(8.73)

and

ax/az

=0,

z = 0

on

the side face

A'

C'N'D'E'.

(8.74)

On

the

side face GLMF in Fig. 8.10 we know

that

x = 0 everywhere but

we

do

not know the shape

of

the surface

FG'L'P'M

in Fig. 8.11.

In

principle, this can

be

determined by using the second boundary condition

on

GLMF

in Fig. 8.10 which

is

acb/ax

= 0, which by a standard change

of

variables leads immediately to

(az/ax)

=0,

x=O

onFG'L'P'M'.

(8.75)

Condition (8.75) suggests a quadratic relationship for small

x on a

constant

cb

line in a constant y-plane (Fig. 8.12) of the form

(8.76)

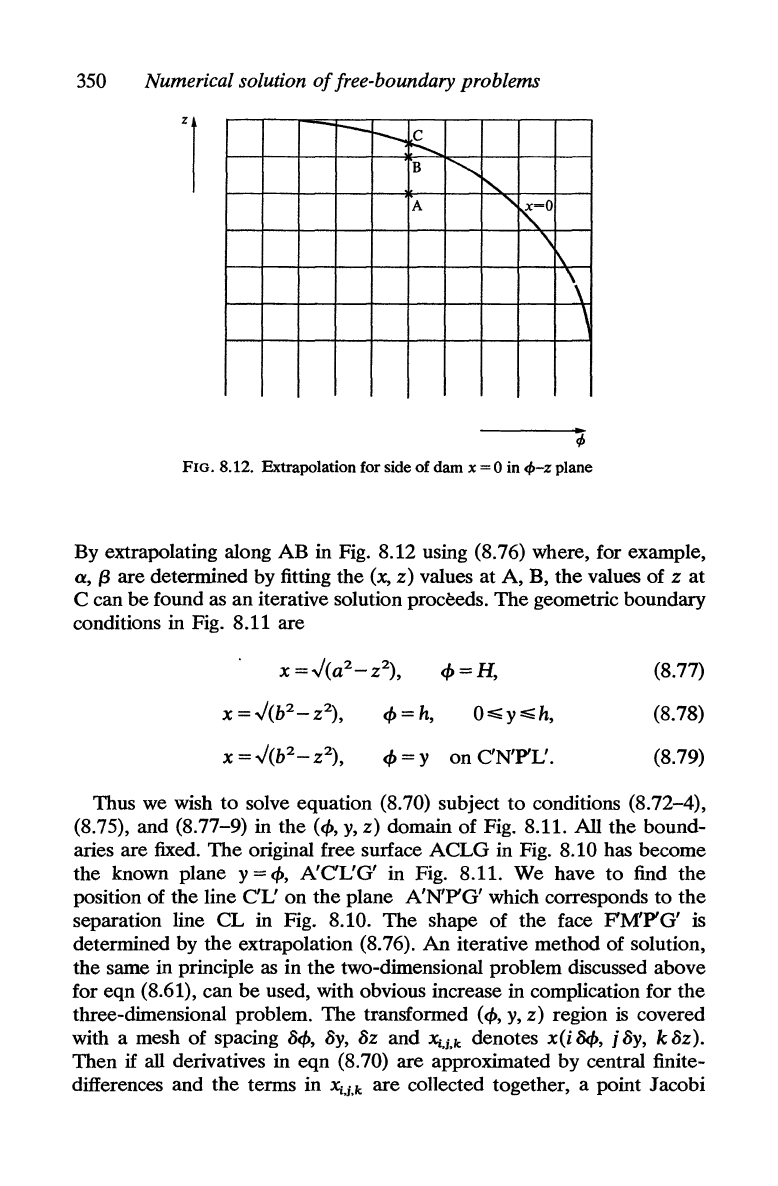
350

Numerical solution

of

free-boundary problems

-

r--

F----

B

~

'"

A

......

x-O

"-

\

\.

\

~

FIG.

8.12. Extrapolation for side of dam

x=O

in

cf>-z

plane

By extrapolating along

AB

in Fig. 8.12 using (8.76) where, for example,

a,

(3

are determined by fitting the

(x,

z)

values

at

A,

B,

the

values of z

at

C can

be

found as

an

iterative solution proceeds.

The

geometric boundary

conditions in Fig. 8.11 are

x =

.j(b

2

-

Z2),

X =

.j(b

2

-

Z2),

</>

=H,

</>

=

h,

</>

= y

on

CN'P'L'.

(8.77)

(8.78)

(8.79)

Thus we wish

to

solve equation (8.70) subject

to

conditions (8.72-4),

(8.75),

and (8.77-9) in

the

(</>,

y,

z) domain

of

Fig. 8.11. All

the

bound-

aries are fixed.

The

original free surface

ACLO

in Fig. 8.10 has become

the known plane

y =

</>,

A'CL'O'

in Fig. 8.11. We have

to

find

the

position of the line

CL'

on

the

plane

A'N'P'O'

which corresponds

to

the

separation line

CL

in Fig. 8.10.

The

shape

of

the face

FM'P'O'

is

determined by

the

extrapolation (8.76).

An

iterative method of solution,

the same in principle

as

in

the

two-dimensional problem discussed above

for eqn

(8.61), can

be

used, with obvious increase in complication for

the

three-dimensional problem.

The

transformed

(</>,

y,

z)

region is covered

with a mesh

of

spacing

&/>,

By,

Bz

and

X;,j,k

denotes

x(i

&/>,

j

By,

k Bz).

Then

if

all derivatives in

eqn

(8.70) are approximated by central finite-

differences and

the

terms in

X;,j,k

are collected together, a point Jacobi

Methods using variable interchange

351

iterative formula corresponding to (8.68) can

be

written

[2(5~2

- 5!2 )

(5X:P2

+ 5!2

{1

+

(5x~f+

(5x;)~

]X~t(

=

(5X~)2{(X~)2_(X;)2}+

(x~f{(5x~)2_(5x;)2+

l}

+ 2

5x~

5x~{xi'+1,j+1,k

-

Xi'+lj-1,k

-

X;:'l,j+l,k

+

Xi'-1,j-1,J

- 2

5x;

5x~{Xi'+l,j,k+l

-

Xi'+l,j,k-1

-

Xi'-1,j,k+1

+

Xi'-1,j,k-1}'

(8.80)

For

convenience,

5x:t = (XI+l,j,k -

x;:'1,j,J/(2

&f»,

etc. have been introduced and

X~j,k

is

the nth iterative value

of

Jii,j,k'

On

the

free surface we have either x = .J(b

2

-

Z2)

or

n+1

n 2(5y f

_1.

(5

y

)2

~:X~j'k+1

=

X~'k-1f

(8.81)

Xi,j,k

=

xi,i-1,k

Xl+1,i+l,k

-

Xi'-lj-1,k

2 5z

Xi+1,i+1,k

Xi-1,i-1,k

from

eqn

(8.72); as in the two-dimensional problem, a one-sided differ-

ence replacement of

(ax/ay)c/>,z

is used to avoid fictitious points. Corres-

ponding modified forms of (8.80) are applied at all mesh points one step

below

the

plane A'N'P'G' and

on

the lower impervious boundary, y =

O.

Use of the extrapolation (8.76) leads to unequal mesh sizes in eqn (8.80)

for points

one

step inside the side face FM'P'G', and in eqn (8.81) for

points

one

step inside the curve P'G'

on

which x =

O.

For

points in the line

A'N', i.e. z = k = 0, fictitious points can

be

avoided when using (8.81)

because

of

(8.74).

The

iterative cycle

is

started by assuming the separation line

eL'

to

be

at

N'P', its lowest possible position, unless prior knowledge suggests a

better

starting position. We thus ensure that the final position of C'L' is

approached from below. We then know that x = .J(b

2

-

Z2)

on

the face

D'N'P'M' and

on

C'N'P'L' and also

that

x = .J(a

2

-

Z2)

on

the face

E'A'G'F.

For

every

other

mesh point within the region and

on

the

remaining parts

of

the boundary, an equat,ion has been derived.

One

iterative cycle involves sweeping along successive i-planes in the order

i = 0, 1, 2,

...

, where i = y = 0 is the lower boundary.

In

each consecutive

plane each mesh point

is

covered in the order i = 0, k = 0, 1, 2,

...

; i = 1,

k

= 0, 1, 2,

...

, and so on.

The

new values

X~tk1

are retained for use in

the

next cycle subject to the proviso

that

on

the boundary plane we take

the

new value

x~N

to

be

X!,;I"l

= min(.J(b

2

-

Z2)

X!,;I"l)

hJ.k

,

1~I.k

since we know

that

Jii,j,k

~.J(b2-

Z2).

On

FG'P'M' new values of Z are

retained for use in the next cycle. Values

of

the solution and of the

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.