Crank J. Free and Moving Boundary Problems
Подождите немного. Документ загружается.


192
Front-fixing methods
moving boundary
that
do not contain s
are
less amenable directly,
but
implicit conditions can
be
rendered explicit by
the
Schatz (1969) transfor-
mation
or
by
repeated
differentiation (Crank
and
Gupta
1972a).
Furzeland (1980) gave detailed comparisons of
the
boundary-fixing
methods in
one
space dimension for
three
test problems from
the
points
of view of accuracy, computing time, convenience of use, etc. Some
of
these results
are
given in Tables
6.2
and
6.3.
5.2. Body-fitted
curvilinear
coordinates
The
one-dimensional coordinate transformations introduced
in
§S.1 are
simple cases
of
the
more
general transformation
of
a curved-shaped
region in two
or
more
dimensiohs into a fixed, rectangular domain. Since
the
new coordinates
are
chosen
to
fit
the
shape of
the
original region,
they
are
commonly called 'body-fitted'
or
'natural' coordinates.
The
original coordinate system (x, y) is transformed into a new system
(~,
1),
which may
be
orthogonal
or
non-orthogonal, such
that
the
curved bound-
aries in
the
(x, y) plane become
(~,
1) coordinate lines. Corresponding
to
the
regular straight-lined
(~,
1) mesh is a curvilinear (x, y) mesh as in Fig.
S.l.
In
moving-boundary problems
the
region changes with time,
but
a fixed
(~,
1) mesh which corresponds
to
a moving (x,
y)
mesh can
be
used for all
time.
The
movements
of
the
boundary
and
of
the
mesh points in
the
original region
appear
only as changes in x
and
y
at
the
corresponding,
fixed,
(~,
1) points
at
each time step.
The
attractions of working in a
simple, straight-lined fixed region such as a rectangle with
no
loss
of
accuracy
in
discretization
near
curved boundaries
are
offset
to
some
eXtent by
the
increased complexity of
the
transformed partial differential
equation
and
boundary conditions, together with
the
additional work
of
generating
the
curvilinear mesh
at
each time step.
But
it is
an
advantage
to
have direct control over
the
(x, y) mesh spacing so that, for example, a
y
o
y.(x)
P'4
(=,
(x,y).
11-11
(x,y)
x-x
«(,11)
"y-y«(,l1)
x
FIG. 5.1. Transfonnation to rectangular mesh
p'
3

Body-fitted curvilinear coordinates
193
finer mesh can
be
used in regions of special interest such as
near
the
moving boundary
or
a singularity.
Following a
pioneer
paper
by
Winslow (1967), extended by
Chu
(1971), successive authors have proposed various ways of using a cur-
vilinear grid. Useful lists of references were given by Thompson, Thames,
and
Mastin (1974)
and
by
Furzeland
(1977a).Oberkampf
(1976) discus-
sed some useful generalized mapping functions. Furzeland
(1977b) sum-
marized some
of
the
transformations, orthogonal
and
non-orthogonal,
that
have
been
proposed.
For
moving-boundary problems attention has
been
focussed mainly
on
non-orthogonal transformations, which
are
conveniently introduced through Laplace's equation for a general depen-
dent
variable
q,
=
q,(x,
y) =
q,(~,
TJ)
satisfying
iPq,
iPq,
-+-=0
ax
2
ay2
.
The
following standard differential relationships exist:
~x
=
YTl/J,
~y
= -x,p,
TJx
= -y,iJ,
TJ
y
=
Xf./J,
(5.21)
(5.22)
(5.23)
where
~
=
a~/ax,
etc.,
and
J is
the
Jacobian
Xf.YTl
-
~YE
=1=
O.
For
example,
given
x =
x(~,
TJ),
we
have
(5.24)
By
solving (5.24) for
d~
and
dTJ
we
obtain
d~
Y
TI
dx-~
dy
=
YTi
dx-~
d
y
,
xEYTl-~YE
J
from which
the
first
of
(5.22) follows immediately and, similarly,
the
other
derivatives in (5.22)
and
(5.23).
Then
we have
dq,
=
q,E
d~
+
q,TI
dTJ
and
so
(5.25)
on
using (5.22).
The
second derivative follows
in
the
standard way since
(5.26)

194
Front-fixing methods
and
similarly for
other
higher derivatives. Using these derivative rela-
tions, Laplace's equation for q,(x, y) transfonns into
where
A =
~~+~~=
(x~+y~)/J2,
B =
2(~TJx
+
~yTJy)
= -2(xl;x" +
YEy
...
)/J
2
,
C =
TJ~+
TJ~
=
(x~+
y~)fJ2,
D =
~
+
~yy,
E =
TJ=
+
TJyy.
(5.27)
(5.28)
(5.29)
(5.30)
(5.31)
Chu (1971)
quoted
expressions for C
and
D
in
tenns
of
xI;,
YI;,
etc. and,
together with Oberkampf (1976), derived similar expressions for
more
general equations
than
Laplace's.
Nonnal
derivatives of
q,
on
a boundary
Y =
g(x)
are
given
by
A..
_
g'
q,x
-
q,y
_ 1 {A.. ( , ) _
A..
('
+
)}
'I'n
-
{1
+
(g')2}~
-
J{l
+
(g')2~
x
'1"1;
g Y
...
+ x" '1"
...
g
YI;
~
(5.32)
where
g'
= dy/dx.
Time derivatives
of
q,(x,
y,
t)
are
transfonned
from a given point (x, y)
to
the
corresponding
(~,
TJ)
point
by
the
relationship
1
(q,t)x,y
=
(<bt)I;
....
-j
(y
...
q,1;
-
YI;q,
...
)(:x:r)E.
...
1
-j
(Xj;q,
...
-
x"q,I;)
(Yt)E.
....
(5.33)
Thus all derivatives of q,(x,
y,
t) can
be
expressed
in
terms of derivatives
at fixed points in
the
transfonned region, whether
the
original (x, y)
domain
and
mesh
are
time dependent
or
not.
Of
the
various transfonnations mentioned by Furzeland (1977b)
the
simplest
one
to
use
in moving-boundary problems is
due
to
Oberkampf
(1976), who chose
~=
x-xe(Y)
x..(y)-xe(Y)
,
Y-Ye(x)
Yu(x)-Ye(x) ,
(5.34)
where Xe.
x..,
Yeo
Yu
are
the
four curved sides in Fig. 5.1.
Even
if, for
example,
the
upper
boundary
Yu
is moving,
the
second
of
(5.34) ensures
that
it is
the
stationary coordinate line
TJ
= 1
in
the
transfonned plane.
In
general, Xe etc. represent sets of discrete values
of
boundary points
and
can
be
deliberately chosen
to
give any required mesh spacing, a facility
which is not available
if
orthogonal transfonnations are used.
It
follows
from (5.34)
that
~,
TJ
are
then
known discrete functions
of
x
and
y,
and
Example
of
use
of
body-fitted coordinates
195
that
the
derivatives
~,
~Y'
etc. needed in
the
coefficients
A-E
are
available as suitable discrete approximations. Finite elements with
bivariate blending functions (Gordon and Hall 1973) provide alternative
mappings
to
(5.34)
and
so do isoparametric curvilinear coordinates (Zien-
kiewicz
and
Phillips 1971).
5.3.
Example
of
use
of
body-fitted coOrdinates
Furzeland (1977b)
took
the
one-phase two-dimensional problem of
Bonnerot
and
Jamet
(1977) set
out
in equations (4.24-28) in §4.3.3 as an
example, with A = 1 in (4.28).
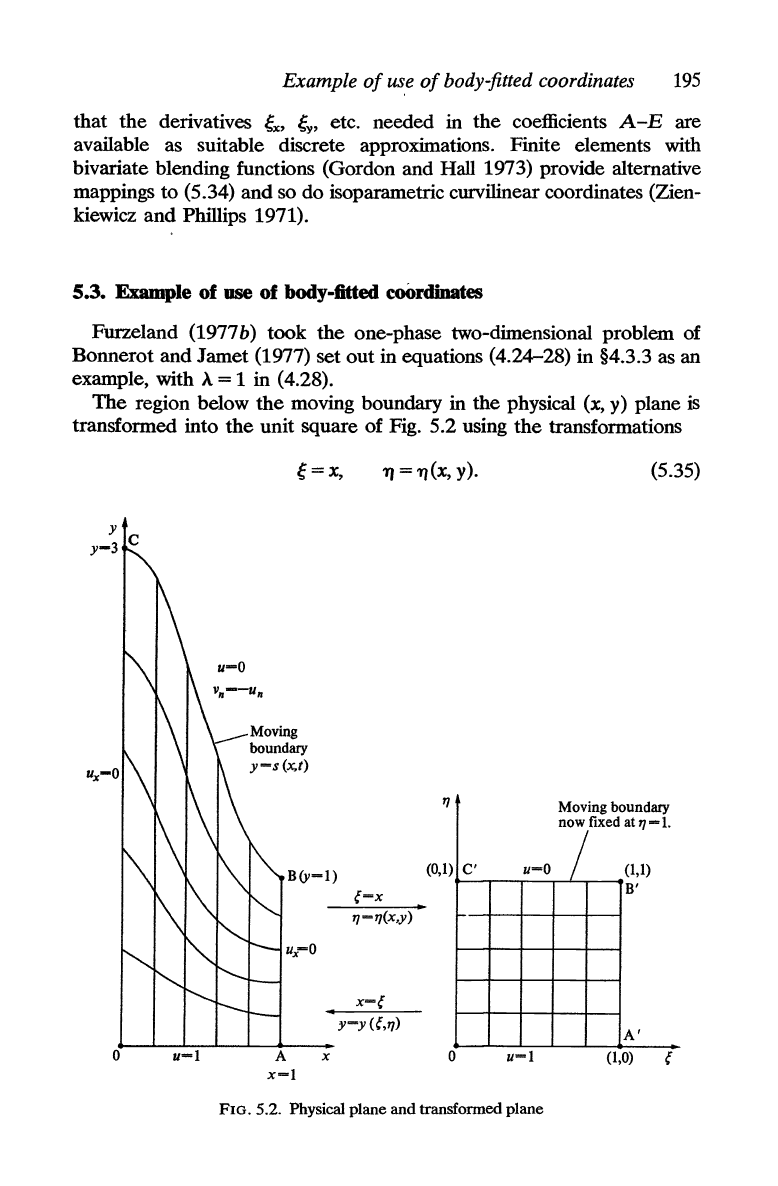
The
region below
the
moving boundary in
the
physical (x, y) plane
is
transformed into
the
unit
square
of
Fig. 5.2 using
the
transformations
~=x,
1/
= 1/(x, y).
(5.35)
u=o
___
Moving
boundary
y-s(x,t)
TJ
Moving boundary
B(y-I)
(0,1)
(-x
nj"'''.'-L
C'
u-O
(1,1)
B'
TJ-TJ(x,y)
ux-O
x=(
y-y«(,TJ)
A'
0
u=1
A
x
0
u-I
(1,0) (
x-I
FIG. 5.2. Physical plane and transformed plane

196 Front-fixing methods
Combining (5.27) and (5.33)
the
heat equation (4.24) becomes
Uc
=
Au~
+
Bu~
+
~"l
+
D'u~
+
E'~,
O:s;;;g:S;;;l,
t>o, (5.36)
where
D'
= D+(XqYt -
Y"l~)/J,
E'
= E +
(y~~
- x,;Yt)/J
(5.37)
and
A-E
are given by (5.28-31) inclusive.
If
now
the
Oberkampf
transformations (5.34) appropriate for this problem are used, i.e.
g=x,
TI
= y/s(x, t),
the
transformed equation (5.36) becomes
Uc
=
au~~
+
bu~
+ c~ +
d~
+
e~,
O:s;;;g:s;;;l,
where
a = 1, b =
-2ys~/S2,
e =
(y/s)~~
+ yJs,
having used
the
facts that
Y"l
= S,
Y~
=
ys~/s
from (5.38).
Similarly, the derivative conditions are
su~
-(ys~~/s)
=0,
g=o,
1,
and
the
moving boundary conditions are
u
=0,
Yt
=-(1
+st)uJs,
(5.38)
t>o, (5.39)
d=O,
(5.40)
(5.41)
(5.42)
Duda
et al. (1975) used
the
transformations (5.38). Hsu, Sparrow,
and
Patankar (1981) combined it with an energy-conserving finite-difference
scheme which was applied by Sparrow
and
Hsu
(1981) to a freezing
problem outside a tube carrying coolant.
With reference
to
an
Nl
X
N2
mesh of size h in
the
square domain of
Fig. 5.2 and denoting
gk
=
kh,
k = 0, 1,
...
,
Nb
and
Tie
=
eh,
e =
0, 1,
...
,N
2
,
suitable approximations for
s€
and
s~~
are
s~~
= (Sk+1-2sk +Sk_l)/h
2
,
k = 1, 2,
...
, N
-1.
(5.43)
At
k = ° and N,
s~
= ° since
Ux
= ° and u = 0.
The
numerical solution
proceeds in time steps
8t
so
that
t = t
n
= n 8t, n = 0,
1,2,
...
, and suitable
approximations are used for the derivatives of
u over the square.
If
the
velocity of
the
moving boundary,
Yt,
on
TI
= 1
at
the
point
9c
is denoted by
(Yt)k>
then
(5.44)
where
(Yt)k
is approximated from (5.42) by using
the
first of (5.43) for
s~

Example
of
use
of
body-fitted coordinates
197
and
either a three-point, end-on formula for
Uq
on
1'/
= 1
or
the standard
'fictitious-point' approximation suggested
by
Furzeland (1977b)
to
pre-
serve
O(h2) accuracy.
The
numerical algorithm becomes:
(i)
given u and s
at
time level n, compute (x, y) values at each
({;,1'/)
mesh point using (5.38);
(ii) compute
the
new position of the moving boundary at time
(n
+
1)
using (5.44) with a discretized form of (5.42);
(iii) use the second of (5.38)
to
calculate the corresponding changes in y
at all mesh points ({;,1'/);
(iv)
solve
the
heat
eqn
(5.39) with coefficients (5.40) by suitably
discretizing
the
time
and
space variables. Return to step (ii) and
repeat for each time level.
Furzeland
(1977b) presented numerical results based
on
this algorithm
and
on
the
use of an alternative 'equipotential' transformation of Wins-
low (1967) instead of the Oberkampf transformation (equation (5.38)).
The
Winslow transformation
is
more expensive in computer time because
an
additional subsidiary equation has to
be
solved
at
each time step, but it
does offer a smoother and more flexible control over
the
curvilinear mesh
spacing. Furzeland
(1977b) found that both his algorithms compared well
with
the
results of Bonnerot and Jamet (1977). Further applications of
the
general method were discussed by Hoffman (1977, Volume
III).
Saithoh (1978) used a version of
the
transformation (5.34) in radial
coordinates which provides a useful way of handling a phase-change
boundary problem within an arbitrarily shaped region.
He
referred to the
earlier work of
Duda
et al. (1975). With reference to Fig. 5.3, where the
coordinates are
r,
</>,
the
region within the fixed boundary r =
B(</»
is
initially occupied by liquid
at
the
freezing temperature.
The
solidification
r
FIG. 5.3. Boundary fixing in radial coordinates

198
Front-fixing methods
boundary is defined by r =
F(
ef>,
t).
In
appropriate non-dimensional terms
the
relevant
set
of equations is
au
=V2U=.!.~
(r
au)
+_1_
cru
at
r ar
ar
r2ef>~
aef>2
'
au
·-=0
aef>
'
ef>
=
0,1,
u
~
uw(ef>,
t),
r=B(ef»,
aF
[
(1
aF)2]
au
u=o
-=St
1+
--
-
, at
ef>oF
aef>
ar
'
r=F(ef>,
t),
where
ef>o
is
the
angular width of the region and St is Stefan's number.
In
two space dimensions
the
new variable
r-
F(ef>,
t)
.,.,
=
B(ef»-
F(ef>,
t)
fixes
the
moving boundary
at
.,.,
= 0
and
the
outer, fixed boundary
at
.,.,
= 1.
The
corresponding transformation in
three
dimensions is
{ = r -
F(
ef>,
6,
t) ,
B(ef>,
6)-F(ef>,
6,
t)
where
(r,
ef>,
6)
are
radial coordinates.
In
the
two-dimensional case
the
transformed system is
au
{1
1 (a.,.,)2} a
2
u
at
=
(B-F)2+
R
aef>
a.,.,
2
{
1
a.,.,
1 a
2
.,.,}
au 2
a.,.,
a
2
u 1 a
2
u
+ r(B -
F)
aef>
+ R
aef>2
a.,.,
+ R
aef> aef>
a.,.,
+ R
aef>2
,
aulaef>
=0,
ef>=0,1; u=uw(ef>,t), .,.,=1;
aF
= St au
_1_
{1 +
()
a!:\
2}
at
a.,.,
B - F
\Fef>o
a;f, J '
R =
(ef>or)2.
u=O,
.,.,=0,
Thus,
the
transformed partial differential equation has
to
be
solved in
the
fixed rectangular region
0~ef>~1,
O~.,.,
~1.
Any
point at which
the
fixed boundary r =
B(ef»
is
not smooth, such as
the
comer
of a square, needs special consideration.
For
the latter case, for
example, Saitoh
(1978) substituted
the
equation
au 1 a
(au)
1
(au)
ar
=
-;:
ar
r
ar
+ r
def>
aef>
-

Isotherm migration method
199
where
(au/acfJ)_
is
the
value
of
the
derivative
at
q,
= 'IT/4-dq,; this
equation expresses
the
heat
balance
of
an element between
r,
r+dr
and
'IT/4,
'IT/4-dq,.
Saitoh (1978) compared his numerical solution for
the
solidification of
a square region
of
liquid with values measured experimentally
and
found
good
agreement.
He
also presented calculated values for some triangular
regions.
5.4. Isotherm migration method
A particular case
of
the
curvilinear transformation depicted in Fig. 5.1
is
one
in which
the
dependent variable u is interchanged with
one
of
the
space-variables, e.g. u = u(x, y) becomes x
=x(u,
y).
In
a one-dimensional time-dependent heat-flow problem
the
tempera-
ture
u can
be
interchanged with
the
space variable x, so
that
the
solution
evaluates
x(u,
t) instead
of
the
more traditional u(x, t).
The
latter expres-
ses
the
time dependence
of
temperature
at
chosen values
of
x;
the
former
denotes how a specified temperature u moves through
the
medium: in
other
words how isotherms migrate. This so-called Isotherm Migration
Method
(IMM) was proposed by Chernousko (1970), independently by
Dix
and
Cizek (1970),
and
subsequently developed
and
extended
to
two
space dimensions by
Crank
et al. (1973, 1975, 1978, 1979)
and
by
Turland
and
Wilson (1977)
and
Turland (1979).
The
IMM
is
particularly suited
to
melting
and
freezing problems since
the
phase
boundary is itself
an
isotherm, provided
the
phase change takes
place
at
a constant temperature.
The
IMM
is, in fact, a boundary-fixing
method
and, in
one
space dimension, x
is
evaluated
at
successive times in
the
fixed domain
O:OS;
u
:os;
1, for example.
As
the
governing equations
are
discretized in temperature
u,
mesh lines are isotherms along which
temperature-dependent
heat
parameters are known in advance
and
so
can
be
handled simply
and
efficiently.
In
other methods they
are
coupled
with
the
evaluation
of
U,
say, in
the
(x,
t) plane.
5.4.1.
IMM
in one space dimension
Consider as
an
illustration
the
one-phase Stefan problem
au=a
2
u.ds=_A
au
u=O,
x=s(t).,
at ax
2
'dt
ax'
u=l,
x=O,
t>O;
u=O,
X>O,
t=O.
(5.45)
Instead
of
writing u = u(x, t) we
take
x = x(u, t) as a new dependent
variable.
By
the
usual partial-derivative relations we have
(5.46)

200
Front-fixing methods
where
(ax/at}u
signifies
the
rate
of change of x with t at constant
u,
i.e.
denotes
the
movement of an isotherm, and finally
(5.47)
Use of (5.46) and (5.47) transforms (5.45) to
ax (aX)-2a2x
at
=
au
au
2
'
O<u<l,
t>o,
(5.48)
dS=_..\exr
1
dt
au'
u=o,
t>o,
(5.49)
x=o,
u=l,
t>o,
(5.50)
and a starting solution is needed for small times as with most finite-
difference methods when there
is
a singularity at x = 0, t = 0.
The
derivatives in (5.48) can
be
approximated by finite differences
to
give, for example, an explicit expression for
xi'+l,
the value of x at
u
= i
8u,
t = (n +
1)
8t in terms of values already available at
(i
8u, n 8t).
The computation proceeds on a mesh of size 8u, 8t in
the
(u, t) plane (Fig.
5.4) and values of
xi'
are calculated
at
the
mesh points using
n+l
n
4'"
(xi'+1-
2X
i'+Xi'-1)
Xi
=
Xi
+
ut
(n
n}2
Xi-l-Xi+l
(5.51)
in general, and from (5.49) on u
= 0, i = 0,
n+l
n ..\8t8u
s
=s
----.
xo-xi
(5.52)
A rigorous analysis of
the
stability of
the
non-linear difference scheme
has not been attempted. Dix and Cizek (1970) applied the heuristic
argument that since a virtual increase in
xi'
must produce an increase in
FIG. 5.4. IMM transformed plane

Isotherm migration method
201
xi+
1
so
the
coefficient
of
xi in (5.51) must be positive and hence
5t
<!(X;-l
-
X;+J
2
.
(5.53)
Inclusion of
the
criterion (5.53) in the computer algorithm gives a simple
way for
the
time step 5t to
be
adjusted automatically as
the
solution
proceeds.
Dix
and Cizek (1970) showed the truncation
error
of
this IMM
is proportional
to
5t
and (5U)2. Crank and Phahle (1973) showed satisfac-
tory agreement between isotherm positions at selected times obtained by
the
IMM with those obtained from the well-known analytical solution
(see (3.12), (3.14».
Conditions
on
a fixed boundary, different from u = 1
on
x = 0 in (5.45)
for example, would call for some but not
a major modification of the
method. Thus a boundary condition
u = g(t) on x = 0, t > 0 would result
in a known
but
curved boundary in
the
(u,
t) plane
on
which x =
O.
Conditions involving derivatives can also be handled.
The
condition
au/ax = 0
on
x = 0 clearly causes difficulties in (5.48) but the value of u at
which
x = 0 at each time level can easily
be
found by expressing u as
the
parabola u = ax
2
+
b,
where a and b are obtained by inserting
the
computed values of x at the two mesh points neighbouring
the
boundary.
This
u value
is
then used in
the
solution of (5.48) at
the
next time level,
albeit with
an
unequal interval in
u.
5.4.2. IMM in multi-dimensional problems
(i)
Partial transformation
of
variables. Crank and
Gupta
(1975) extended
the
IMM
to
the
solution of general heat-flow problems in two space
dimensions with particular reference to Stefan problems.
As
an example,
they computed numerical results for
the
solidification
of
a square prism of
fluid initially at
the
melting temperature, u =
1,
throughout and the
surface
of
which
is
subsequently maintained at u = 0 below
the
melting
temperature.
Solutions are required of
the
equation
au
a
2
u a
2
u
-=-+-
at
ax
2
ay2 ,
subject
to
the
boundary conditions
u
=0
on
g(x, y) =
(x
2
-1)(y2_1)
=0,
t;;O:O,
where
the
prism occupies
the
space -1.,;;x.;;;1, -1";;y.,;;1, and
u=l
on
f(x,
y, t) = 0,
t>O
(5.54)
(5.55)
(5.56)
where
f(x,
y,
t) = 0
is
the
phase-change surface at time
t.
Initially we have
f(x,
y,O)=g(x,
y)=O,
t=O.
(5.57)
