Crank J. Free and Moving Boundary Problems

142

Analytical solutions

where the surface of the cylinder, r =

a,

is

maintained at temperature

- U(t),

Yo

is

the solution of

and

4K

f'

yolnyo+1-Yo=Lpa2-'o

Udt',

(3.169)

(3.170)

The

first

tenn

in (3.168)

is

again the steady-state approximation to

y,

since the appropriate steady-state solution

is

u=

U In(s/r)

In(s/a) ,

from which (3.169) follows

on

using the usual conditions

au/ar=

(Lp/K)

ds/dt, u = 0 on the solidification boundary

and

integrating the

resulting differential equation,

(Lp/K)

ds/dt = - U/{s In(s/a)}, remember-

ing that

y = (s/a)2. )

Pekeris and Slichter (1939) show graphs of

Yo

In

Yo

+ 1 -

Yo

and of

f(yo)/Yo for

Yo

ranging between 0 and 700, together with a plot of the

growth of ice according

to

the steady-state approximation for a choice of

physical conditions.

The

idea of postulating temperature profiles was extended to multi-

dimensional problems of crystal growth by Horie and Chehl (1975). They

chose the profiles either by introducing a 'penetration depth'

or

by using

the heat-flow equation itself.

3.6.2. Spatial subdivision

Solomon (1978) extends

the

Megerlin method in a manner analogous

to

Bell's (1978) extension of

the

heat-balance method by spatial subdivi-

sion. Whereas Bell divided

the

temperature range into equal intervals,

Solomon uses equal subdivisions of the space range and postulates

an

approximate temperature profile in each subdivision.

Taking the one-phase Stefan melting problem

he

denotes the

jth

subdivision by

Xj-l

<x<Xj,

j=1,2,

...

,N,

(3.171)

where

Xj(t) =

(jfN)s(t),

j = 0, 1, 2,

...

,

N,

and lets

(3.172)

Approximate solutions

143

Continuity of u

i

and of its first derivative are required at x = Xj, where u

i

also satisfies

the

heat-flow equation. Also u

1

and

UN

satisfy the conditions

u(O, t) =

Uo>

Ut,

- K

dU(S,

t)/dX =

pL

ds/dt respectively, where

Uf

is

the

freezing temperature. From a series of recurrence relations for the

llj, b

j

,

and the assumptions that the

Uj

are a constant for each j, and that

s

=

2A

.J(kt), Solomon derives the following transcendental equation for a

root

A,

which depends on

N:

C A

2

[ {

2A

2

} N (

2{3A

2)

L

(Uo-uJ=

N

1+3

1+

3~

11

1

+

N2

N-l

N (

UA2)]

+2

L

11

1+-

. (3.173)

/3=2t'=/3+1

~

Writing

c(Uo-Ut)/(L.J7T)=F

N

(A) from (3.173) Solomon tabulates

FN,N=O,

1,2,3,

for

0:,;;:;A.;;;2

at intervals of 0.2 and notes slow con-

vergence but concludes that

limits of 10

per

cent relative accuracy are

given by

f4

for

N=

1,

L~1T

(uo-uJ-

4

5

.6 for

N=2,

for

N=3.

However, this range of apparently up to 1000

OF

even for N = 1

is

not a

serious practical limit for

the

melting of ice

or

a typical wax. However,

caution is advised for

the

recrystallization of iron, say from a

to

'Y

type,

where the allowable temperature range would

be

around 100

OF

for N = 1

and 130

OF

for N =

3.

This approach, based on spatial subdivision,

is

closely similar to the use

of cubic splines by Crank and Gupta

(1972b).

Solomon applied spatial subdivision to

the

constant boundary-flux

problem for which results obtained by the Megerlin method without

subdivision have been given in Table 3.5.

In

fact, he used equation

(3.166) as a starting solution for a Runge-Kutta scheme for handling the

spatial-subdivision equations. Some of his results are shown in Table 3.6

TABLE

3.6

Moving-boundary

position

s(t)

N=1

N=2

N=5

0 0 0

0

4

2.404

2.244 2.241

8 4.094

3.708

3.723

12 5.5549

4.928 4.961

16 6.865

6.009 6.058

20 8.085 6.995 7.058

24

9.233

7.911 7.987

28 10.324 8.772

' 8.860

144

Analytical solutions

for various values

of

N. Solomon concluded

that

N

==

2 produces accepta-

ble accuracy, though a heat-balance check reveals

heat

discrepancies for

N

= 2 of around

16

per

cent for t = 4 rising to 35

per

cent for t = 28,

but

reducing

to

3.6

per

cent for N = 4

and

only 2

per

cent for N = 6

and

10.

3.6.3.

The inverse Stefan problem

Kreith

and

Romie (1955) described

an

iterative

method

for improving

the

steady-state approximation for

the

inward solidification

of

a cylinder

and

a sphere when

the

rate

of

movement

of

the

interface is constrained

to

be

constant.

The

problem is

to

determine

the

necessary

temperature-time

dependence which must

be

imposed

on

the

surface

of

the

cylinder

or

sphere

to

maintain a constant

rate

of

solidification.

The

physical condition

on

the

interface is - K aTtaR =

pL

dS/d-T

with aTtaR = g = constant, T =

time,

and

S is

the

thickness

of

the

frozen zone.

Expressed in non-dimensional terms,

the

cylinder

problem

requires

the

solution

of

the

following equations with G = gcro/L, where

ro

is

the

radius

of

the

cylinder, c is specific

heat,

and

T-T

f

u=--

rog ,

R

r=-

ro'

KgT

t=--

pLro'

S

s=-,

ro

G=gcr

o

L'

where

T

f

is the fusion

temperature

and

To

is

the

temperature

on

the

outer

surface R =

ro:

!~

(r

au) = G au,

r

ar

at

au/ar=

-ds/dt=

+1, u

=0,

r=

1-s,

u=o, s=o,

t=O.

(3.174)

(3.175)

(3.176)

It

is clear from (3.175)

and

(3.176)

that

the

position

of

the

solidification

interface

at

time t is given

by

r = 1 - s = 1 +

t.

Kreith

and

Romie express

the

temperature u

by

the

series

(3.177)

each

term

of

which is related

to

the

preceding

term

by

the

equation

!~(r

au,,) = G au,,-1 (3.178)

r

ar

at

and

hence, after integration,

by

u,,=G

r

drI'

J

1

+

t

r

1+t

au,,-1 d

r--

r

at

'

n>l.

(3.179)

The

first term U1

of

the

series is

obtained

by

setting G = 0

in

(3.178),

which leads immediately

to

r

au/ar

= constant = 1 - s, since

on

r = 1 - s,

Approximate solutions

145

au/ar

= 1, and so, remembering that u = 0 on

1-

s,

it follows that

U1

=

</>

In(r/</»,

</>=1+t.

(3.180)

This term

is

the steady-state approximation and the new variable

</>

is

the

radius of the solidification front. The next four terms given by Kreith and

Romie are

r<1(r2

) r

</>2

r2}

U2=-'l

4+~</>2

In

</>

+"2-2"

U

3

=

G2{(-&</>3+i</>~)ln

.!:.+~</>3_-&</>r2_~}

</>

64</>

U4

=

-G

3

{

C31f4</>4

+

H</>2r2

+ rlsr4)ln ;

~-I.4

.l1.

2 2 7 4

r6

2}

+

2304'1'

-

256</>

r -

128

r

+ 2304

</>

_

G4{(.l2.a.-I.5+~-I.3

2+..12.

4-1.)1

r

Us

-

9216'1'

384'1'

r

512

r

'I'

n

</>

2325 5 31 3 2

77

4

+ 73728

</>

+ 4608

</>

r - 2048 r

</>

1r

6

1

r8}

1536

</>

73 728

</>

(3.181)

For

values of

G;;;;.

-1.5

the

first

five

terms are stated by Kreith

and

Romie

to

give

the

temperature U to an accuracy within one

or

two

per

cent of

the exact value.

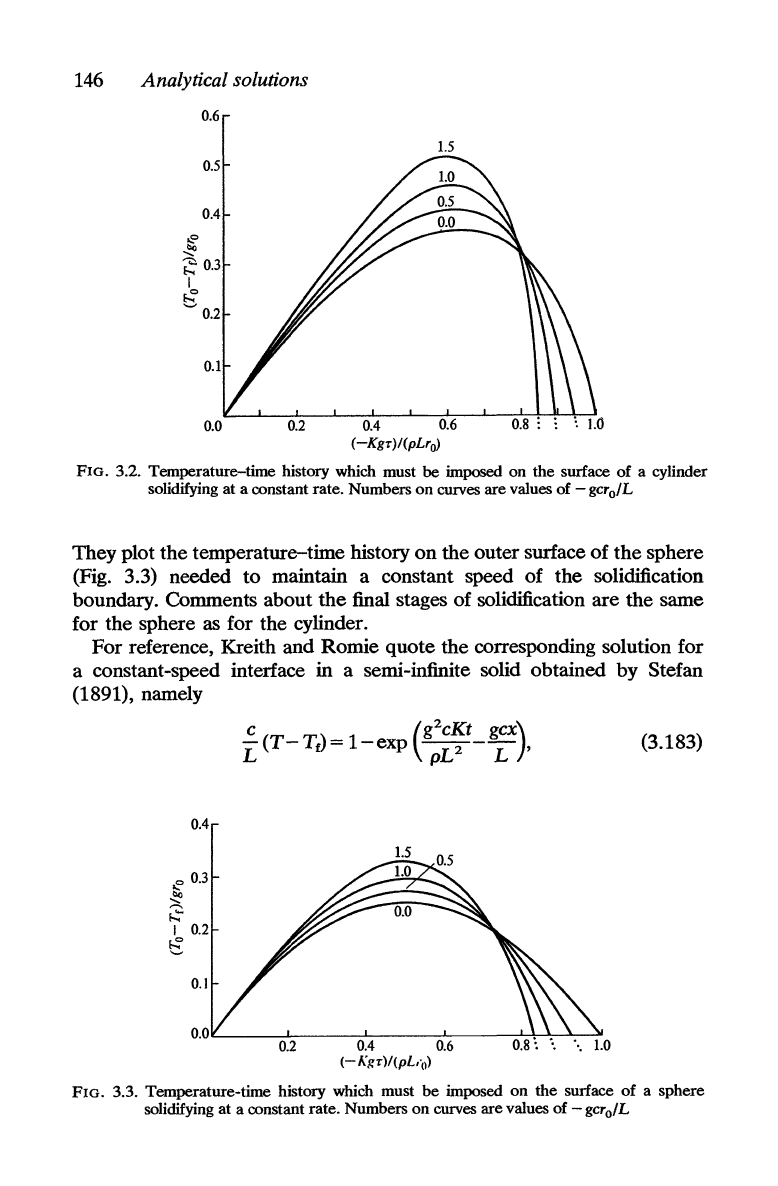
They plot the required temperature-time histories on the cylinder

surface for values of G from zero to

-1.5,

i.e. a range of constant speeds

of the solidification front. These are reproduced in Fig. 3.2. They show

that in order

to

solidify the cylinder completely in such a way that the

interface maintains a constant speed

to

the end, the surface temperature

has

to

be raised above the melting temperature. Such a condition

is

not

allowed for in the problem as formulated in equations

(3.174-6). This

behaviour, of course,

is

a consequence of the speeding up of the interface

as it approaches the centre when

the.

outer surface temperature

is

maintained constant.

By the same method, Kreith and Romie

(1955) obtain

the

temperature

profile for a constant-speed solidification front in a sphere expressed as

U = _

~

G

n

r

n

+

1

n

,+

~ ~

(_

W-1Gi+1ri-1</>i+2

2.i

+ j

~

.

n=l

(n+2).

i=-lj=O

(,+2).J.

(3.182)

146

Analytical solutions

~

0.6

0.5

0.4

~

0.3

I

~

0.2

1.5

0.2

0.4 0.6

(-Kgr)/(pLro)

FIG. 3.2. Temperature-time history which must

be

imposed on the surface of a cylinder

solidifying at a constant rate. Numbers

on

curves are values of

-gcro/L

They plot the temperature-time history on the outer surface of

the

sphere

(Fig. 3.3) needed to maintain a constant speed of

the

solidification

boundary. Comments about

the

final stages of solidification are the same

for the sphere as for the cylinder.

For reference, Kreith and Romie quote the corresponding solution for

a constant-speed interface in a semi-infinite solid obtained by Stefan

(1891), namely

0.4

e

0.3

~

I

0.2

C

0.1

c

(g2cKt

gCX)

-(T-T

f

)=1-exp

----

L

pL

2

L'

(3.183)

0.2

0.4

0.6

(-

K[:r)/(pLio)

FIG. 3.3. Temperature-time history which must be imposed on the surface

of

a sphere

solidifying at a constant rate. Numbers

on

curves are values of - gcro/L

Approximate solutions

147

where

U£

is

the

melting temperature and T

is

time.

The

temperature

on

the

outer

surface, x = 0, clearly has

to

be

L (

g2

c

Kt\

To=Tf+;

1-exp

pL

2

)'

i.e.

it

takes negative values which increase exponentially with time.

3.6.4. Fictitious diffusivity approximations

Churchill

and

Gupta

(1977) based approximate solutions of Stefan

problems

on

classical solutions of

the

heat-flow equation in the absence of

phase changes. They introduced fictitious heat diffusivities.

As

an

exam-

ple,

the

two-phase Neumann problem set out in equations (3.1-6) in §3.2

reduces

to

a simple heat-flow problem in

the

special case

of

zero latent

heat

and

uniform properties.

The

solidification boundary, as such, no

longer exists

but

the

motion

of

the melting temperature is derivable from

the

well-known solution of

the

simple heat-flow problem satisfying all the

boundary conditions for

L =

O.

It is convenient

to

rewrite

the

problem

of

§3.2 in terms

of

a melting temperature U

m

and so

to

rewrite the solutions

(3.12) and (3.13) as

U

1

-

Ul

erf{x/2(klt)~}

U

1

-

U

m

erfA

U2

- U

2

_

erfc{x/2(~t)!}

U

m

-U

2

-

erfc{A(kl/~~}'

(3.184)

(3.185)

where

the

condition (3.5) has

been

replaced by U = U

2

, X

~CO,

t ... O and

U

1

>

Um>

U

2

;

also A

=a/(2kt)

so that (3.10) has become s

=2A(k

1

t);

and

hence

the

equation for A is now

_e___

2 - m

2P2

C

2

e 1 2

'IT

(3 186)

-).2

(U

U

){K

}!

-).2k

/k

!L

A erf A U

m

-

U

1

K1PICl

A erfc{A(k

1

/k

2

)!}

Cl(U

m

-

U

1

) •

instead of (3.11). From (3.184) we find that the flux F on x = 0 is

F=-K

1

aUl=Kl(U\-U~.

(3.187)

ax

(-7Tk

1

t)"erf A

For

L = 0, A = co, SUbscripts can

be

dropped and instead

of

(3.184) and

(3.185) we have

the

standard solution (Crank 1975, p. 32)

U1-u

{X}

U

1

-

U

2

erf

2(kt)!

(3.188)

and

(3.187) is replaced by

F =

K(

U

1

-

U

2

)/(

'lTkt)t.

(3.189)

148

Analytical solutions

Putting u =

Urn

in (3.188) gives for

the

motion

of

the

Urn

isotherm, which

is

the

solidification boundary, in

the

hypothetical case

of

zero latent

heat

(3.190)

Comparison

of

(3.187)

and

(3.189) shows

that

the

latter equation would

give

the

exact surface

heat

flux for a finite latent

heat

if

Kpc = KIPICI{(U

I

-

U~/(UI-

U

2

)erf

AV,

which can

be

secured by letting K =

KI

and

taking a fictitious value k

f

for

the

thermal diffusivity k given

by

k =

(kl(U

I

-

U~erf

,\.)2

f

(UI-U~

.

(3.191)

An

alternative interpretation is

that

a fictitious

heat

capacity

Cf

is

to

be

used where

CI(UI-U~

Cf =

{(UI

-

U~erf

,\.}2 ,

(3.192)

coupled with putting

Kp

=

KIPI'

These

procedures cannot yield

the

complete temperature distribution

correctly. However,

the

exact value for

the

position s(t) of

the

solidifica-

tion boundary can

be

obtained from equation (3.190), for U

I

=/=

Urn,

by

choosing

k. = ki

~rrl{(UI-

~~/(U2-

UI}t

(3.193)

Churchill

and

Gupta

(1977) proposed

that

these fictitious properties

can

be

used

to

approximate

the

behaviour in

other

geometries

and

for

different boundary conditions.

In

this way,

the

solutions for non-linear

Stefan problems can

be

deduced from

the

well-known analytical

and

numerical solutions of simple heat-flow problems.

The

choice

of

k

f

or

k.

depends

on

whether accuracy in

the

surface

heat

flux

or

in

the

location of

the

phase-change interface is desired. H

both

quantities

are

important,

both

fictitious values

can

be

employed. Churchill and

Gupta

(1977) cited

the

problems of

the

freezing

of

a liquid outside a cylinder and

the

freezing

of

a quarter-space as examples

of

satisfactory agreement between results

obtained using

the

fictitious

heat

parameters defined

in

(3.191)

and

(3.193)

and

those

that

other

authors

have

calculated by numerical

methods.

Churchill

and

Evans (1971) tabulated

and

plotted values of

,\.

and

erf,\.

for a wide range of

the

parameters

L/{CI(U

I

-

U~},

{(U

2

-

U~/(Um

UI)){(K2C2P~/(KICIPI)}!'

and

kIlk2

which facilitate

the

use of

the

fictiti-

ous

heat

parameters.

Their

values for

104,\.

are

tabulated in

Table

3.7

to

Approximate solutions

149

TABLE

3.7

Values

of

10

4

A,

the solution

of

(3.186),

for

values

of

L/C

1

(U

1

-

Urn),

kl/k2'

and p

={(U

2

-

UrJ/(U

m

-

Ul)}{(K2C2P2)/(KlClPl)}~

L

C1(UI-UrJ

kl/k2

p=0.5

p=1.0

p=1.5

p=2.0

p=3.0 p=5.0

p=10.0

0.0

9451

6584

4991

3982

2803

1731

0.0 0.5

7371

5137

3973

3245

2376

1547

0.0

1.0

6841

4769

3708

3046

2253

1488

0.0

1.5

6504 4536

3538

2917

2172

1447

0.0

2.0

6256

4365

3413

2821

2110

1415

0.5

5686 4403

3010

0.5

1.0

5456

4179

3392

2855

2168

1461

803

0.5 1.5

5295

4028

3266

2752

2096

1422

789

0.5

2.0

5168

3912

3170

2673 2041

1392

778

0.5

3.0

4972 3738

2555

0.5

4.0

4822

3607

2467

0.5

5.0

4700

3502

2397

0.5 6.0 4596

3415

2338

1.0

0.5

4835

3933

2826

1.0

4699

3778

3152

2701

2092

1435

793

1.0

1.5

4599

3669 3054

2615

2029

1399

780

1.0

2.0

4519

3584

2977

2548

1981 1371

770

1.0

3.0

4391

3452

2448

1.0

4.0

4290

3351

2371

1.0

5.0

4205

3268

2310

1.0

6.0

4133

3198

2258

1.5

1.0

4198

3480

2961

2571

2026

1411

793

1.5

4129 3396

2881

2498

1969 1377

780

1.5

2.0

4072

3330

2818

2442

1925 1350

777

2.0

0.5

3903

3338

2550

2.0

1.0

3834

3246

2804

2461

1966 1389

789

2.0

1.5

3782 3180

2737

2398

1915 1356

776

2.0

3739 3126

2683

2348

1875

1331

766

2.0

3.0

3612 3041

2271

2.0

4.0

3669

2974 2212

2.0

5.0

3564 2918

2163

2.0

6.0

3521

2870

2121

3.0

1.0

3329 2899

2557

2280

1863 1347

780

3.0

1.5

3296

2853

2507

2232

1821

1318

768

3.0

2.0

3268

2815

2467

2193

1787

1295

758

5.0

1.0

2732

2455

2220

2021

1702

1276

764

5.0

1.5

2715

2428

2189

1988

1671

1252

753

5.0

2.0

2700

2405

2163

1962

1646

1233

744

10.0

1.0

2037

1891 1761

1643

1442

1143

728

10.0

1.5

2030

1880

1746 1627

1424

1127

719

10.0

2.0

2024

1870

1734

1613

1410 1113

711

150 Analytical solutions

three

or

four significant figures with

the

headings adjusted

to

the

present

nomenclature.

Ockendon (1975) drew attention to

the

possible non-unifonnity of

the

limit for zero latent

heat

in one-phase problems.

3.6.5. Perturbation methods; asymptotic solutions; stability

There

appear

to

be

very few solutions of Stefan problems in

the

form

of series expansions derived by perturbation methods. Even for

one-

dimensional problems, the analysis

is

very complicated and often prohibi-

tive beyond

the

first approximation. Fox (1975) quotes Jiji (1970), who

succeeded in obtaining only

the

zero-order approximation in a problem

of

the solidification of a fluid surrounding a cold solid cylinder. Fleishman,

Gingrich, and

Mahar

(1978) and Fleishman and Mahar (1977)

report

applications of perturbation linearization methods to obtain approximate

solutions of two-dimensional steady-state free-boundary problems. Ellip-

tic partial differential equations of

the

form div(K grad u) + f = 0

are

considered in which K and/or f depend discontinuously

on

u and a small

parameter e appears in a boundary condition. References

are

given by

Fleishman

et al. (1978) to earlier papers

on

the

one-dimensional versions

of similar problems.

Friedman (1964), Ockendon (1975), and Elliott and Ockendon (1982)

draw attention

to

the

value

of

asymptotic methods in which either

the

space

or

time variables

or

some physical parameters are taken

to

be

large

or

small. They can sometimes illuminate aspects of behaviour

not

re-

vealed by weak and variational methods. Indeed, numerical methods in

general frequently need

to

be

supplemented by small

or

large time

or

distance solutions near singularities

at

zero time, for example,

or

when

approaching a boundary

at

infinity. Rubinstein (1971), Evans

et

al.

(1950), Cannon and

Hill

(1967), Cannon, Douglas, and

Hill

(1967), and

others have studied asymptotic expansions for large and small indepen-

dent variables. Howarth and Poots (1976), in considering

the

solidifica-

tion of a half-space of liquid cooling by black-body radiation, obtained

both large and small-time series solutions. They then applied a process of

renormalization in which certain coefficients in the large-time series

are

chosen so

that

this solution, when formally expanded for small times, is

made

to

agree as far as possible with

the

small-time solution. A useful

uniformly valid expansion

is

obtained.

Ockendon (1980) and Elliott and Ockendon (1982) explored certain

instabilities of moving boundaries in a selection of problems by perturba-

tion and asymptotic techniques. Chadam and Ortoieva (1982) adapted

Rubinstein's

(1982b) stability analysis

to

show

that

planar melting

is

stable but planar solidification

is

unstable unless surface tension

is

included. Small amplitude perturbations are also analysed by Turland and

Approximate solutions

151

Peckover (1980), who refer to several earlier

paper-s

including an exten-

sive non-linear stability analysis of

the

freezing of a dilute binary alloy by

Wollkind and Segel (1970).

Rasmussen and McGeough (1981) examined non-linear stability in

electro-forming problems by perturbation and numerical techniques.

We discuss now in some detail the application of perturbation techni-

ques

to

two problems in which the ratio of the latent heat

to

the sensible

or specific

heat

is

large, as it often

is

in practice.

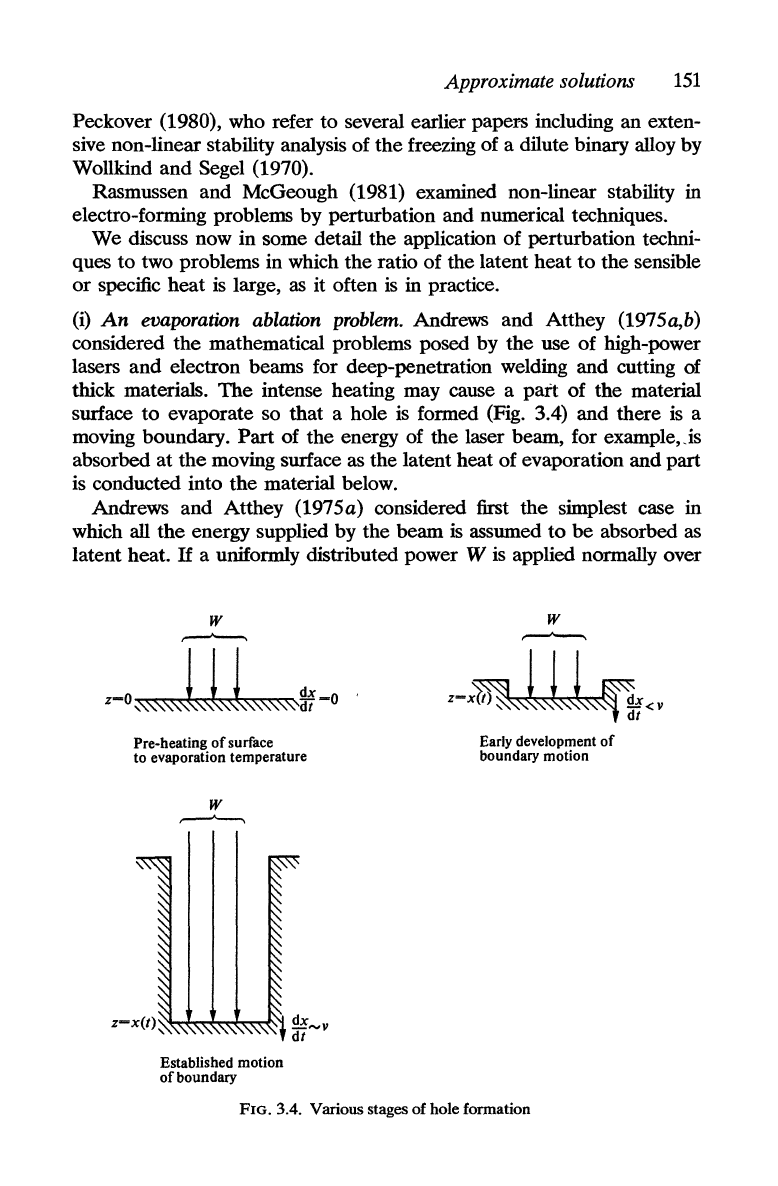
(i)

An

evaporation ablation

problem.

Andrews and Atthey (1975a,b)

considered

the

mathematical problems posed by the use of high-power

lasers

and

electron beams for deep-penetration welding and cutting of

thick materials.

The

intense heating may cause a part of the material

surface

to

evaporate so that a hole

is

formed (Fig. 3.4) and there

is

a

moving boundary.

Part

of the energy of the laser beam, for example,js

absorbed at

the

moving surface as the latent heat of evaporation and part

is conducted into

the

material below.

Andrews and Atthey

(1975a) considered first the simplest case

in

which all

the

energy supplied by the beam

is

assumed

to

be

absorbed as

latent heat. H a uniformly distributed power W

is

applied normally over

w

,.---"-.

~~%~~-M-<l

Pre-heating

of

surface

to evaporation temperature

Established motion

of

boundary

w

z-x~

I I I

~~<v

rW~I

Early development

of

boundary motion

FIG. 3.4. Various stages of hole formation

Crank J. Free and Moving Boundary Problems

Подождите немного. Документ загружается.