Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.


23. Illumination of the moon’s surface: The table
given indicates the percent of the Moon that is
illuminated for the days of a particular month, at a
given latitude. (a) Use a graphing calculator to find
a sinusoidal regression model. (b) Use the model to
determine what percent of the Moon is illuminated
on day 20. (c) Use the maximum and minimum
values with the period and an appropriate horizontal
shift to create your own model of the data. How do
the values for A, B, C, and D compare?
model shown, where D(t) is the distance t min after
entering orbit. Negative values indicate it is south
of the equator, and the distance D is actually a two-
dimensional distance, as seen from a vantage point
in outer space. The value of B depends on the
speed of the satellite and the time it takes to
complete one orbit, while represents the
maximum distance from the equator. (a) Find the
equation model for a satellite whose maximum
distance north of the equator is 2000 miles and that
completes one orbit every 2 hr ( ). (b) How
many minutes after entering orbit is the satellite
directly above the equator ? (c) Is the
satellite north or south of the equator 257 min after
entering orbit? How far north or south?
26. Biorhythm theory: P(d) 50 sin(Bd) 50
Advocates of biorhythm theory believe that human
beings are influenced by certain biological cycles
that begin at birth, have different periods, and
continue throughout life. The classical cycles and
their periods are physical potential (23 days),
emotional potential (28 days), and intellectual
potential (33 days). On any given day of life, the
percent of potential in these three areas is
purported to be modeled by the function shown,
where P(d) is the percent of available potential on
day d of life. Find the value of B for each of the
physical, emotional, and intellectual potentials and
use it to see what the theory has to say about your
potential today. Use day
since last birthday.
27. Verifying the amplitude formula: For the
equations from Examples 1 and 2, use the
minimum value (x, m) to show that
is equal to . Then verify this
relationship in general by substituting for
A, for D.
M m
2
M m
2
1
y D
A
m D
A
d 365.251age2 days
3D1t2 04
P 120
A
710 Modeling With Technology III Trigonometric Equation Models MWTIII–10
24. Connections between weather and mood: The
mood of persons with SAD syndrome (seasonal
affective disorder) often depends on the weather.
Victims of SAD are typically more despondent in
rainy weather than when the Sun is out, and more
comfortable in the daylight hours than at night. The
table shows the average number of daylight hours
for Vancouver, British Columbia, for 12 months of
a year. (a) Use a calculator to find a sinusoidal
regression model. (b) Use the model to estimate the
number of days per year (use )
with more than 14 hr of daylight. (c) Use the
maximum and minimum values with the period and
an appropriate horizontal shift to create a model of
the data. How do the values for A, B, C, and D
compare?
Source: Vancouver Climate at www.bcpassport.com/vital.
1 month 30.5 days
25. Orbiting distance north or south of the equator:
D(t) A cos(Bt) Unless a satellite is placed in a
strict equatorial orbit, its distance north or south of
the equator will vary according to the sinusoidal
Day % Illum. Day % Illum.
128 1934
455 22 9
782 25 0
10 99 28 9
13 94 31 30
16 68
Month Hours Month Hours
1 8.3 7 16.2
2 9.4 8 15.1
3 11.0 9 13.5
4 12.9 10 11.7
5 14.6 11 9.9
6 15.9 12 8.5
College Algebra & Trignometry—
cob19529_ch0MWT_701-710.qxd 12/29/08 11:49 AM Page 710 epg HD 049:Desktop Folder:NSS_28-12-08:

Applications of
Trigonometry
CHAPTER OUTLINE
7.1 Oblique Triangles and
the Law of Sines 712
7.2 The Law of Cosines; the
Area of a Triangle 724
7.3 Vectors and Vector Diagrams 736
7.4 Vector Applications and
the Dot Product 752
7.5 Complex Numbers in
Trigonometric Form 765
7.6 De Moivre’s Theorem and
the Theorem on nth Roots 776
7
7
CHAPTER CONNECTIONS
When an airline pilot charts a course, it’s not
as simple as pointing the airplane in the right
direction. Wind currents must be taken into
consideration, and compensated for by
additional thrust or a change of heading to
equalize the force of the wind and keep the
plane flying in the desired direction. The
effect of these forces working together can be
modeled using a carefully drawn vector
diagram, and with the aid of trigonometry, a
pilot can easily determine any adjustments in
navigation needed. This application appears
as Exercise 85 in Section 7.3
Check out these other real-world connections:
Tracking Large Game in a Wildlife Preserve
(Section 7.1, Exercise 50)
Calculating Distances between Cities
Using Satellite Information
(Section 7.2, Exercise 37)
Forces Required to Tow a Van out of a Ditch
(Section 7.3, Exercise 81)
Measuring Forces Used by Contestents
in a Tough-Man Contest
(Section 7.4, Exercise 37)
711
College Algebra & Trignometry—
cob19529_ch07_711-723.qxd 11/19/08 2:20 AM Page 711 epg HD 049:Desktop Folder:Satya 18/11/08:

Many applications of trigonometry involve oblique
triangles, or triangles that do not have a angle. For
example, suppose a trolley carries passengers from
ground level up to a mountain chateau, as shown in
Figure 7.1. Assuming the cable could be held taut,
what is its approximate length? Can we also determine
the slant height of the mountain? To answer questions
like these, we’ll develop techniques that enable us to
solve acute and obtuse triangles using fundamental
trigonometric relationships.
A. The Law of Sines and Unique Solutions
Consider the oblique triangle ABC pictured in
Figure 7.2. Since it is not a right triangle, it seems
the trigonometric ratios studied earlier cannot be
applied. But if we draw the altitude h (from
vertex B), two right triangles are formed that share
a common side. By applying the sine ratio to angles
A and C, we can develop a relationship that will help
us solve the triangle.
For we have or For
we have or Since both products are equal to h, the transitive
property gives which leads to
since
divide by ac
simplify
Using the same triangle and the altitude drawn from C (Figure 7.3), we note a
similar relationship involving angles A and B: or and
or . As before, we can then write If is obtuse,
the altitude h actually falls outside the triangle, as shown in Figure 7.4. In this case,
consider that from the difference formula for sines (Exercise 55,
Section 6.3). In the figure we note yielding h c sin sin1180° 2
h
c
sin ,
sin1180° 2 sin
A
sin A
a
sin B
b
.h a sin Bsin B
h
a
h b sin A,sin A
h
b
sin A
a
sin C
c
c sin A
ac
a sin C
ac
h h c sin A a sin C
c sin A a sin C,
h a sin C.sin C
h
a
C
h c sin A.sin A
h
c
A
90°
712 7-2
Learning Objectives
In Section 7.1 you will learn how to:
A. Develop the law of
sines, and use it to
solve ASA and AAS
triangles
B. Solve SSA triangles (the
ambiguous case) using
the law of sines
C. Use the law of sines to
solve applications
7.1 Oblique Triangles and the Law of Sines
College Algebra & Trignometry—
23 67
2000 m
Figure 7.1
h
b
A
B
C
ac
Figure 7.2
h
b
A
B
C
a
c
Figure 7.3
h
a
A
C
B
b
c
180 ␣
␣
Figure 7.4
WORTHY OF NOTE
As with right triangles,
solving an oblique triangle
involves determining the
lengths of all three sides and
the measures of all three
angles.
cob19529_ch07_711-723.qxd 11/19/08 2:20 AM Page 712 epg HD 049:Desktop Folder:Satya 18/11/08:
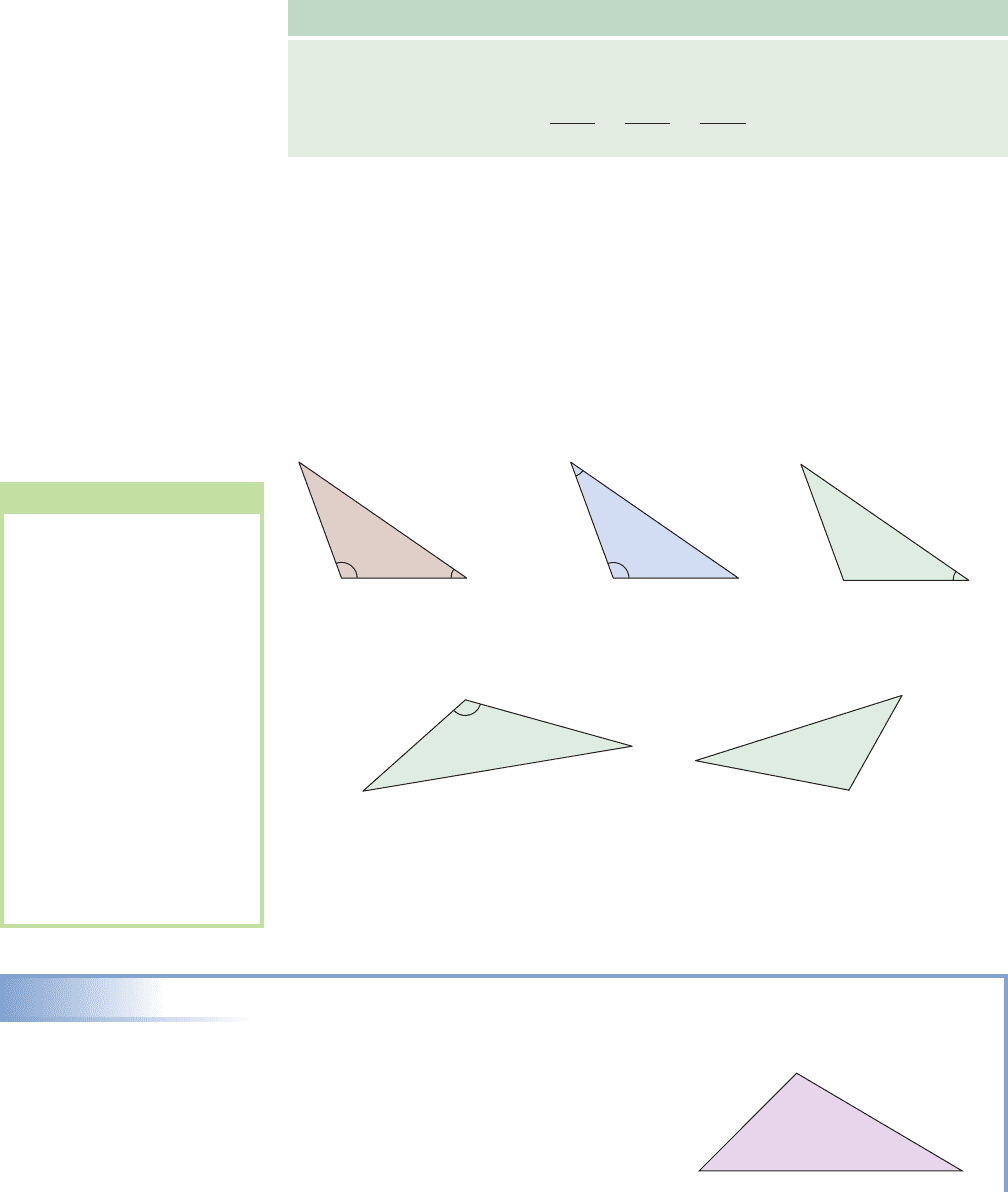
College Algebra & Trignometry—
7-3 Section 7.1 Oblique Triangles and the Law of Sines 713
and the preceding relationship can now be stated using any pair of angles and corre-
sponding sides. The result is called the law of sines, which is usually stated by combing
the three possible proportions.
The Law of Sines
For any triangle ABC, the ratio of the sine of an angle to the side opposite that angle
is constant:
As a proportional relationship, the law requires that we have three parts in order
to solve for the fourth. This suggests the following possibilities:
1. two angles and an included side (ASA)
2. two angles and a side opposite one of these angles (AAS)
3. two sides and a angle opposite one of these sides (SSA)
4. two sides and an included angle (SAS)
5. three sides (SSS)
Each of these possibilities is diagrammed in Figures 7.5 through 7.9.
sin A
a
sin B
b
sin C
c
WORTHY OF NOTE
When working with triangles,
keeping these basic proper-
ties in mind will prevent
errors and assist in their
solution:
1. The angles must sum to
.
2. The combined length of
any two sides must exceed
the length of the third side.
3. Longer sides will be
opposite larger angles.
4. This sine of an angle
cannot be greater than 1.
5. For , the
equation y sin has two
solutions in ( ) that
are supplements.
0°, 180°
y 10, 12
180°
Since applying the law of sines requires we have a given side opposite a known
angle, it cannot be used in the case of SAS or SSS triangles. These require the law of
cosines, which we will develop in Section 7.2. In the case of ASA and AAS triangles,
a unique triangle is formed since the measure of the third angle is fixed by the two
angles given (they must sum to ) and the remaining sides must be of fixed length.
EXAMPLE 1
Solving a Triangle Using the Law of Sines
Solve the triangle shown, and state your answer using a table.
Solution
This is not a right triangle, so the standard
ratios cannot be used. Since and
are given, we know
With
and side a, we have
A180° 1110° 32°2 38°.
A C
B
180°
B
C
A
Angle
Side
Angle
ASA
B
C
A
Angle
Angle
Side
AAS
B
C
A
Side
Side
Angle
SSA
Side
Side
Angle
SAS
Side
Side
Side
SSS
Figure 7.5
Figure 7.8 Figure 7.9
Figure 7.6 Figure 7.7
b
A
B
C
c
110
39.0 cm
32
cob19529_ch07_711-723.qxd 11/19/08 2:20 AM Page 713 epg HD 049:Desktop Folder:Satya 18/11/08:
714 CHAPTER 7 Applications of Trigonometry 7-4
law of sines applied to and
substitute given values
multiply by 39b
divide by
result
Repeating this procedure using shows side In table
form we have
Now try Exercises 7 through 24
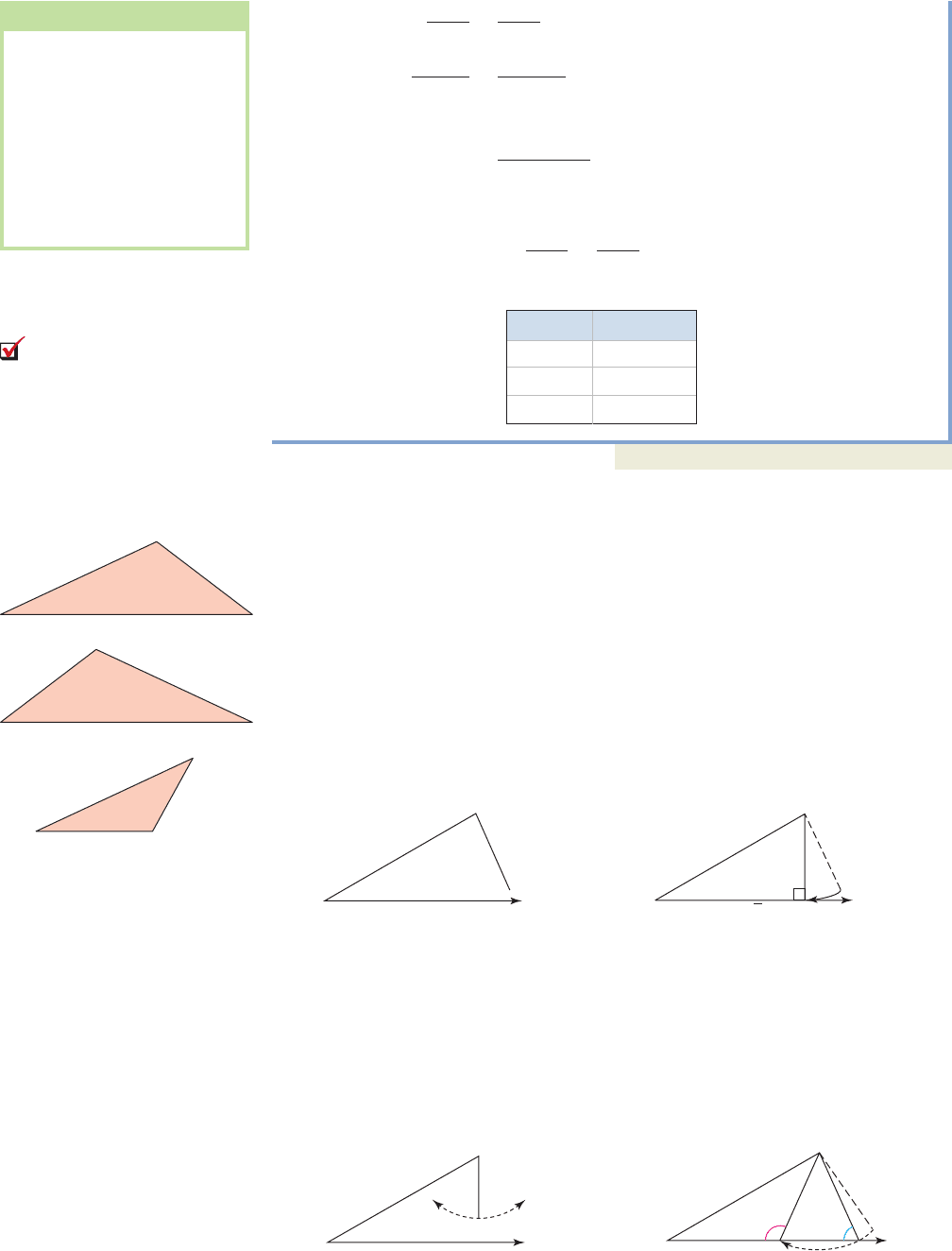
B. Solving SSA Triangles—The Ambiguous Case
To understand the concept of unique and nonunique solutions regarding the law of
sines, consider an instructor who asks a large group of students to draw a triangle with
sides of 15 and 12 units, and a nonincluded angle. Unavoidably, three different
solutions will be offered (see Figure 7.10). For the SSA case, there is some doubt as
to the number of solutions possible, or whether a solution even exists.
To further understand why, consider a triangle with side
and side a opposite the angle (Figure 7.11—note the length of side b is yet to be
determined). From our work with 30-60-90 triangles, we know if it is
exactly the length needed to form a right triangle (Figure 7.12).
a 15 cm,
30°
c 30 cm, A 30°,
25°
c 33.6 cm.
sin A
a
sin C
c
b 59.5
sin 38° b
39 sin 110°
sin 38°
b sin 38° 39 sin 110°
sin 38°
39
sin 110°
b
BA
sin A
a
sin B
b
Angles Sides (cm)
c 33.6C 32
b 59.5
B 110
a 39.0
A 38°
WORTHY OF NOTE
Although not a definitive
check, always review the
solution table to ensure
the smallest side is opposite
the smallest angle, the
largest side is opposite the
largest angle, and so on. If
this is not the case, you
should go back and check
your work.
A. You’ve just learned to
develop the law of sines and
use it to solve ASA and AAS
triangles
15
15
15
12
12
12
25
25
25
30
C
A
B
c 30 cm
a
b
30
60
One
solution
C
A
B
c 30 cm
b 15√3
a 15 cm
30
C
A
B
c 30 cm
a 10 cm
No
solution
b
30
C
1
A
B
c 30 cm
b
a 20 cm
Two
solutions
C
2
By varying the length of side a, we note three other possibilities. If side
no triangle is possible since a is too short to contact side b (Figure 7.13),
while if two triangles are possible since side a will then
intersect side b at two points, C
1
and C
2
(Figure 7.14).
For future use, note that when two triangles are possible, angles C
1
and C
2
must
be supplements since an-isosceles triangle is formed. Finally, if side it willa 7 30 cm,
15 cm 6 side a 6 30 cm,
a 6 15 cm,
Figure 7.10
Figure 7.11 Figure 7.12
Figure 7.13
Figure 7.14
College Algebra & Trignometry—
cob19529_ch07_711-723.qxd 11/19/08 2:20 AM Page 714 epg HD 049:Desktop Folder:Satya 18/11/08:

7-5 Section 7.1 Oblique Triangles and the Law of Sines 715
intersect side b only once, forming the obtuse triangle shown in Figure 7.15, where
we’ve assumed Since the final solution is in doubt until we do further work,
the SSA case is called the ambiguous case of the law of sines.
EXAMPLE 2
Analyzing the Ambiguous Case of the Law of Sines
Given triangle ABC with and side
a. What length for side a will produce a right
triangle where ?
b. How many triangles can be formed if side
c. If side how many triangles
can be formed?
d. If side how many triangles
can be formed?
Solution
a. Recognizing the sides of a 45-45-90 triangle are in proportion according to
1x:1x: side a must be 100 mm for a right triangle to be formed.
b. If it will be too short to contact side b and no triangle is possible.
c. As shown in Figure 7.16, if it will contact side b in two distinct
places and two triangles are possible.
d. If it will contact side b only once, since it is longer than side c
and will “miss” side b as it pivots around (see Figure 7.17). One triangle is
possible.
Now try Exercises 25 and 26
For a better understanding of the SSA (ambiguous) case, scaled drawings can ini-
tially be used along with a metric ruler and protractor. Begin with a horizontal line
segment of undetermined length to represent the third (unknown) side, and use the pro-
tractor to draw the given angle on either the left or right side of this segment (we chose
the left). Then use the metric ruler to draw an adjacent side of appropriate length,
choosing a scale that enables a complete diagram. For instance, if the given sides are
3 ft and 5 ft, use 3 cm and 5 cm instead If the sides are 80 mi and
120 mi, use 8 cm and 12 cm and so on. Once the adjacent side is drawn,
start at the free endpoint and draw a vertical segment to represent the remaining side.
A careful sketch will often indicate whether none, one, or two triangles are possible (see
the Reinforcing Basic Concepts feature on page 751).
11 cm 10 mi2,
11 cm 1 ft2.
B
a 145 mm,
a 120 mm,
a 90 mm,
12
x,
a 145 mm,
a 120 mm,
a 90 mm?
C 90°
c 10012
mm,A 45°
a 35 cm.
Figure 7.15
Figure 7.16 Figure 7.17
B
b
A
C
c 30 cm
30
a 35 cm
45
C
A
B
a
?? mm
c 100√2
45
C
1
C
2
A
B
a 120 mm
c 100√2
45
Misses
side b
B
b
A
C
1
a 145 mm
c 100√2
College Algebra & Trignometry—
WORTHY OF NOTE
The case where three angles
are known (AAA) is not con-
sidered since we then have a
family of similar triangles,
with infinitely many solutions.
cob19529_ch07_711-723.qxd 11/19/08 2:20 AM Page 715 epg HD 049:Desktop Folder:Satya 18/11/08:
716 CHAPTER 7 Applications of Trigonometry 7-6
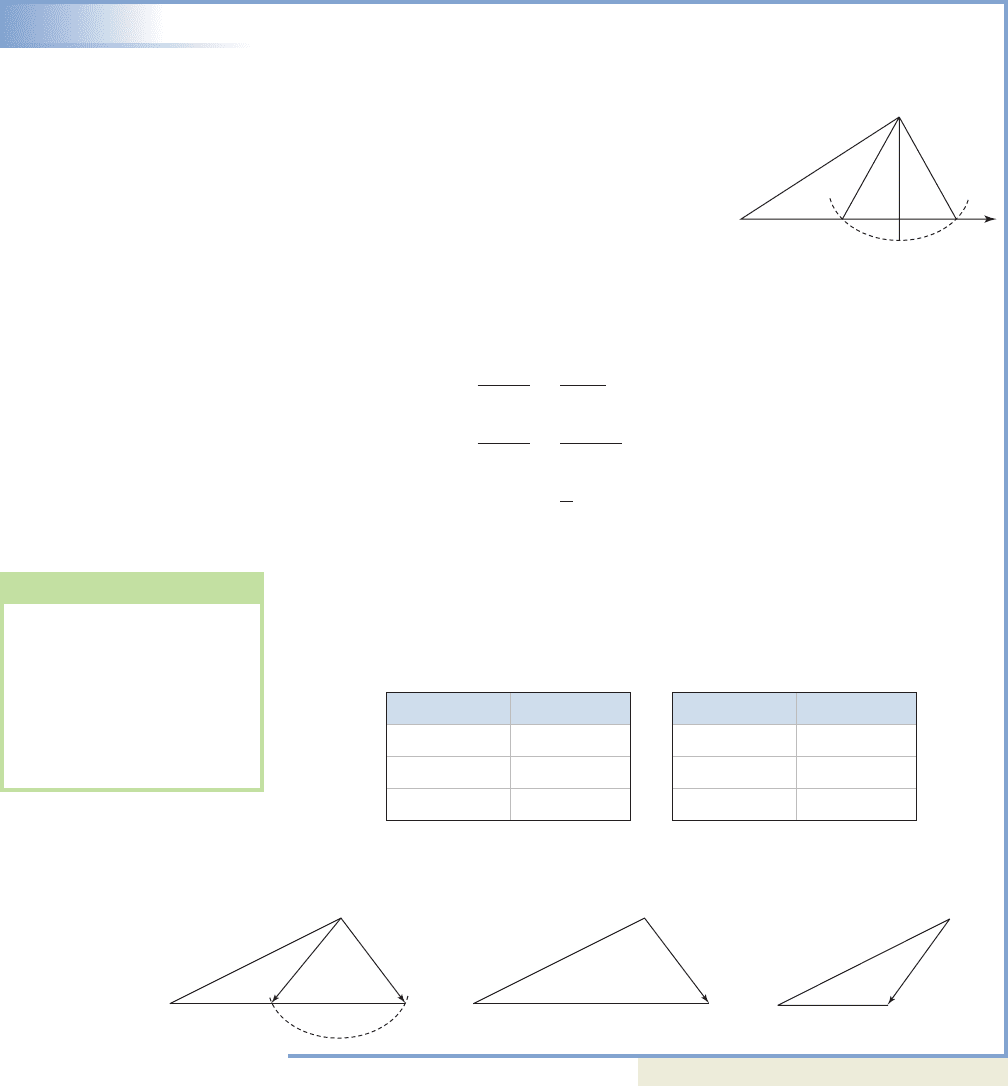
EXAMPLE 3
Solving the Ambiguous Case of the Law of Sines
Solve the triangle with side ft, side ft, and
Solution
Two sides and an angle opposite are given (SSA),
and we draw a diagram to help determine the
possibilities. Draw the horizontal segment of
some length and use a protractor to mark
Then draw a segment 10 cm long
(to represent ft) as the adjacent side of
the angle, with a vertical segment 6 cm long from
the free end of b (to represent ft). It seems
apparent that side c will intersect the horizontal side in two places (see figure), and
two triangles are possible. We apply the law of sines to solve the first triangle,
whose features we’ll note with a subscript of 1.
law of sines
substitute
solve for sin B
1
apply arcsine
Since we know These values give and
as the measures of and , respectively. By once again applying the
law of sines to each triangle, we find side ft and ft. See
Figure 7.18.
Now try Exercises 27 through 32
Admittedly, the scaled drawing approach has some drawbacks—it takes time to
draw the diagrams and is of little use if the situation is a close call. It does, however,
offer a deeper understanding of the subtleties involved in solving the SSA case. Instead
of a scaled drawing, we can use a simple sketch as a guide, while keeping in mind the
properties mentioned in the Worthy of Note on page 713.
a
2
51.0a
1
125.7
A
2
A
1
23.5°
100.5°B
2
128.5°.B
1
B
2
180°,
B
1
51.5°
sin B
1
5
3
sin 28°
sin B
1
100
sin 28°
60
sin B
1
b
sin C
c
c 60
b 100
C 28°.
C 28.0°.c 60b 100
28
C
A
c 60 ft
b 100 ft
B
1
Angles Sides (ft)
c 60
C 28
b 100
B
2
128.5°
a
2
51.0A
2
23.5°
Angles Sides (ft)
c 60
C 28
b 100
B
1
51.5°
a
1
125.7°A
1
100.5°
WORTHY OF NOTE
In Example 3, we found
using the property that states
the angles in a triangle must
sum to We could also
view B
1
as a QI reference
angle, which also gives a
QII solution of
1180 51.52128.5.
180.
B
2
28.0
B
1
C
B
2
A
c 60 ft
b 100 ft
100.5
51.5
a
1
≈ 125.7 ft
First solution
28.0
B
1
C
A
1
c 60 ft
b 100 ft
23.5
128.5
a
2
≈ 51.0 ft
Second solution
28.0
B
2
C
A
2
c 60 f
t
b 100 ft
Figure 7.18
College Algebra & Trignometry—
cob19529_ch07_711-723.qxd 11/19/08 2:20 AM Page 716 epg HD 049:Desktop Folder:Satya 18/11/08:
7-7 Section 7.1 Oblique Triangles and the Law of Sines 717
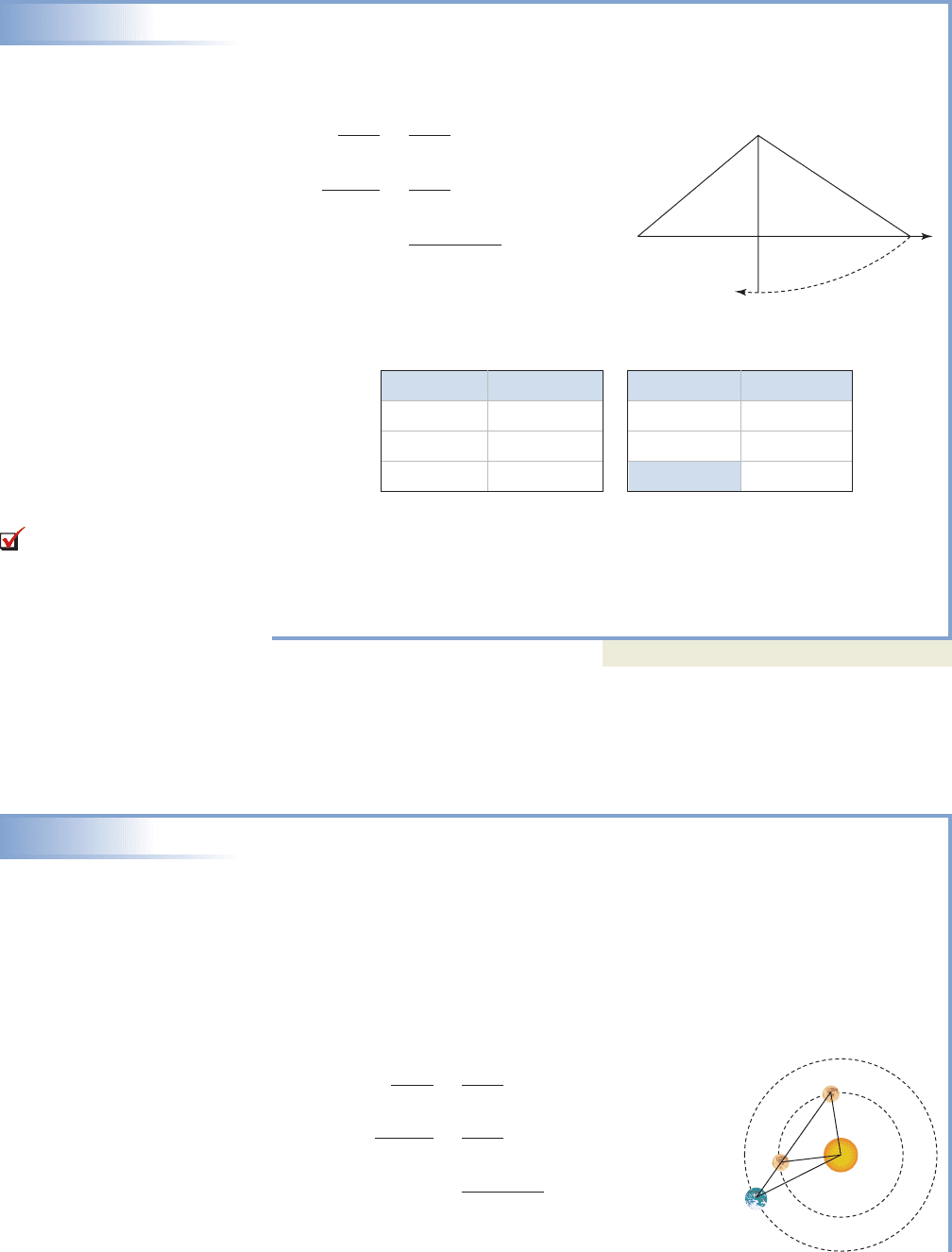
EXAMPLE 4
Solving the Ambiguous Case of the Law of Sines
Solve the triangle with side ft, side ft, and
Solution
The information given is again SSA, and we apply the law of sines with this in mind.
law of sines
substitute
solve for sin B
apply arcsine
This is the solution from Quadrant I. The QII solution is about
At this point our solution tables have this form:
It seems reasonable to once again find the remaining angles and finish by
reapplying the law of sines, but observe that the sum of the two angles from the
second solution already exceeds This means no
second solution is possible (side a is too long). We find that and
applying the law of sines gives a value of ft.
Now try Exercises 33 through 44
C. Applications of the Law of Sines
As “ambiguous” as it is, the ambiguous case has a number of applications in engi-
neering, astronomy, physics, and other areas. Here is an example from astronomy.
EXAMPLE 5
Solving an Application of the Ambiguous Case—Planetary Distance
The planet Venus can be seen from Earth with the naked eye, but as the diagram
indicates, the position of Venus is uncertain (we are unable to tell if Venus is in the
near position or the far position). Given the Earth is 93 million miles from the Sun
and Venus is 67 million miles from the Sun, determine the closest and farthest
possible distances that separate the planets in this alignment. Assume a viewing
angle of and that the orbits of both planets are roughly circular.
Solution
A close look at the information and diagram shows a SSA case. Begin by applying
the law of sines where Earth, Venus, and Sun.
law of sines
substitute given values
solve for sin V
apply arcsine
V 25.4°
sin V
93 sin 18°
67
sin 18°
67
sin V
93
sin E
e
sin V
v
S SV SE S
18°
c
1
331.7
C
1
104.3°,
180°: 40° 144.3° 188.3°!
1180 35.72° 144.3°.
B
1
35.7°
sin B
200 sin 40°
220
sin 40°
220
sin B
200
sin A
a
sin B
b
A 40°.b 200a 220
Angles Sides (ft)
c
1
C
1
b 200
B
1
35.7°
a 220
A 40
Angles Sides (ft)
c
2
C
2
b 200
B
2
144.3°
a 220
A 40
40
B
1
A
a
C
a 220 ft
b 200 ft
B. You’ve just learned how
to solve SSA triangles (the
ambiguous case) using the
law of sines
Sun
Venus
Venus
Earth
67
67
93
College Algebra & Trignometry—
cob19529_ch07_711-723.qxd 11/19/08 2:20 AM Page 717 epg HD 049:Desktop Folder:Satya 18/11/08:

718 CHAPTER 7 Applications of Trigonometry 7-8
This is the angle V
1
formed when Venus is farthest away. The angle V
2
at the closer
distance is . At this point, our solution tables have this form:
For S
1
and S
2
we have (larger angle) and
(smaller angle). Re-applying the law of sines
for s
1
shows the farther distance between the planets is about 149 million miles.
Solving for s
2
shows that the closer distance is approximately 28 million miles.
Now try Exercises 47 and 48
EXAMPLE 6
Solving an Application of the Ambiguous Case— Radar Detection
As shown in Figure 7.19, a radar ship is 30.0 mi off shore when a large fleet of
ships leaves port at an angle of
a. If the maximum range of the ship’s radar is 20.0 mi,
will the departing fleet be detected?
b. If the maximum range of the ship’s radar is 25.0 mi,
how far from port is the fleet when it is first detected?
Solution
a. This is again the SSA (ambiguous) case. Applying the
law of sines gives
law of sines
solve for
result
No triangle is possible and the departing fleet will not be detected.
b. If the radar has a range of 25.0 mi, the radar beam will intersect the projected
course of the fleet in two places.
law of sines
solve for
apply arcsine
This is the acute angle related to the farthest point from port at which the
fleet could be detected (see Figure 7.20). For the second triangle, we
have (the obtuse angle) giving a measure of
for angle . For d as the side opposite
we have
law of sines
solve for d
simplify
This shows the fleet is first detected about 7.6 mi from port.
Now try Exercises 49 and 50
There are a number of additional, interesting applications in the exercise set
(see Exercises 51 through 70).
7.6
d
25 sin 11.9°
sin 43°
sin 43°
25
sin 11.9°
d
180° 1125.1° 43°2 11.9°
180° 54.9° 125.1°
54.9°
sin sin
30 sin 43°
25
sin 43°
25
sin
30
sin 1.02299754
sin sin
30 sin 43°
20
sin 43°
20
sin
30
43.0°.
S
2
180 118 154.6°2 7.4°
S
1
180 118 25.4°2 136.6°
180° 25.4° 154.6°
Angles Sides (10
6
mi)
s
1
S
1
v 93
V
1
25.4°
e 67E 18
Angles Sides (10
6
mi)
s
2
S
2
v 93
V
2
154.6°
e 67E 18
Radar
20 mi
Radar
ship
Por
t
Fleet
30 mi
43.0
Figure 7.19
Radar
25 mi
Radar
ship
Port
30 mi
125.1
43.0
␣
Figure 7.20
C. You’ve just learned how
to use the law of sines to
solve applications
College Algebra & Trignometry—
cob19529_ch07_711-723.qxd 11/19/08 2:20 AM Page 718 epg HD 049:Desktop Folder:Satya 18/11/08:
7.1 EXERCISES
Fill in each blank with the appropriate word or phrase.
Carefully reread the section if needed.
1. For the law of sines, if two sides and an angle
opposite one side are given, this is referred to as
the case, since the solution is in doubt
until further work.
2. Two inviolate properties of a triangle that can be
used to help solve the ambiguous case are: (a) the
angles must sum to and (b) no sine ratio
can exceed .
3. For positive k, the equation has two
solutions, one in Quadrant and the other
in Quadrant .
sin k
4. After a triangle is solved, you should always check
to ensure that the side is opposite the
angle.
5. In your own words, explain why the AAS case
results in a unique solution while the SSA case
does not. Give supporting diagrams.
6. Explain why no triangle is possible in each case:
a.
b.
a 7–, b 9–, c 22–
A 42°, B 57°, C 81°,
a 14¿, b 22¿, c 18¿
A 34°, B 73°, C 52°,
7-9 Section 7.1 Oblique Triangles and the Law of Sines 719
CONCEPTS AND VOCABULARY
DEVELOPING YOUR SKILLS
Solve each of the following equations for the unknown
part (if possible). Round sides to the nearest hundredth
and degrees to the nearest tenth.
7. 8.
9. 10.
11. 12.
Solve each triangle using the law of sines. If the law of
sines cannot be used, state why. Draw and label a
triangle or label the triangle given before you begin.
13. side cm 14. side m
15. side in.
16.
17.
B 60°
A 30°
b 1013
A 108° B 64°
B 47° A 38°
b 385a 75
sin 38°
125
sin B
190
sin C
48.5
sin 19°
43.2
sin B
3.14
sin 105°
6.28
sin 63°
21.9
sin C
18.6
sin 52°
b
sin 30°
12
sin 32°
15
sin 18.5°
a
18.
19. 20.
side mi
side mi
21. 22.
side km
23.
24.
C 19.6°
a 42.7
B 103.4°
B 63.4°c 1512
c 12.9B 45°
A 20.4°A 45°
7.2 m
98
27
19 in.
33
102
89 yd
29
121
126.2 mi
13
22
0.8 cm
56
112
27.5 cm
37
47
College Algebra & Trignometry—
cob19529_ch07_711-723.qxd 12/27/08 15:34 Page 719
