Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.

cob19413_ch03_399-410.qxd 22/10/2008 08:46 AM Page 410 EPG 204:MHDQ069:mhcob%0:cob2ch03:

Exponential and
Logarithmic
Functions
CHAPTER OUTLINE
4.1 One-to-One and Inverse Functions 412
4.2 Exponential Functions 424
4.3 Logarithms and Logarithmic Functions 436
4.4 Properties of Logarithms; Solving
Exponential/Logarithmic Equations 451
4.5 Applications from Business, Finance, and
Science 467
4
4
CHAPTER CONNECTIONS
The largest purchase that most individuals
will make in their lifetime is that of a car or
home. The monthly payment P required to
amortize (pay off) the loan can be calculated
using the formula
where A is the amount financed; t is the time
in years; and , where r is the annual
rate of interest. This study of exponential
and logarithmic functions will help you
become a more knowledgeable consumer.
This application appears as Exercise 53 in
Section 4.5.
Check out these other real-world connections:
Calculating the Effects of Inflation
(Section 4.2, Exercises 87 and 88)
Calculating the Intensity of Sound
(Section 4.3, Exercises 87 to 90)
Calculating the Proper Ventilation of a Home
(Section 4.3, Exercise 97)
Calculating Freezing Time for Water Puddles
(Section 4.4, Exercise 120)
R
r
12
P
AR
1 11 R2
12t
411
College Algebra—
cob19413_ch04_411-490.qxd 29/10/2008 08:59 AM Page 411 EPG 204:MHDQ069:mhcob%0:cob2ch04:
Consider the function . If , the equation becomes
and the corresponding value of x can be found using inverse operations. In this section,
we introduce the concept of an inverse function, which can be viewed as a formula for
finding x-values that correspond to any given value of f(x).
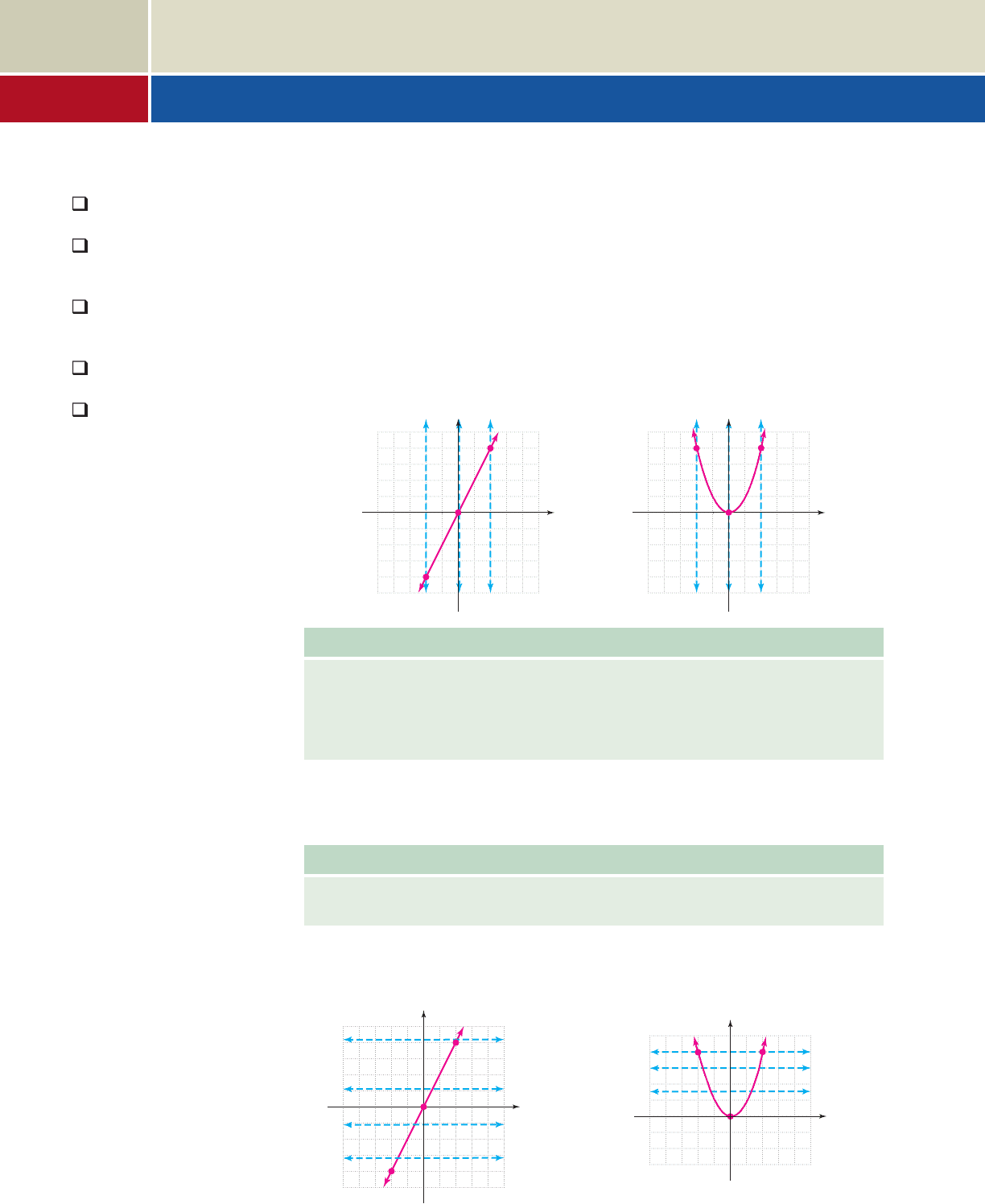
A. Identifying One-to-One Functions
The graphs of and are shown in Figures 4.1 and 4.2. The dashed, ver-
tical lines clearly indicate both are functions, with each x-value corresponding to only
one y. But the points on have one characteristic those from do not—
each y-value also corresponds to only one x (for , 4 corresponds to both and
2). If each element from the range of a function corresponds to only one element of
the domain, the function is said to be one-to-one.
Figure 4.1 Figure 4.2
One-to-One Functions
A function f is one-to-one if every element in the range corresponds to only one
element of the domain.
In symbols, if then , or
if , then .
From this definition we note the graph of a one-to-one function must not only pass a
vertical line test (to show each x corresponds to only one y), but also pass a horizon-
tal line test (to show each y corresponds to only one x).
Horizontal Line Test
If every horizontal line intersects the graph of a function in at most one point, the
function is one-to-one.
Notice the graph of (Figure 4.3) passes the horizontal line test, while the
graph of (Figure 4.4) does not.y x
2
y 2x
f 1x
1
2 f 1x
2
2x
1
x
2
x
1
x
2
f 1x
1
2 f 1x
2
2
5
5
5
5
(2, 4)
(0, 0)
(2, 4)
x
y
5
5
5
5
(0, 0)
(2, 4)
(2, 4)
x
y
2y x
2
y x
2
y 2x
y x
2
y 2x
2x 3 7,f 1x2 7f 1x2 2x 3
4.1 One-to-One and Inverse Functions
412 4-2
College Algebra—
Learning Objectives
In Section 4.1 you will learn how to:
A. Identify one-to-one
functions
B. Explore inverse
functions using ordered
pairs
C. Find inverse functions
using an algebraic
method
D. Graph a function and its
inverse
E. Solve applications of
inverse functions
55
5
1
5
x
y
(0, 0)
(2, 4)
(2, 4)
542135 4 3 2 1
3
2
1
5
4
3
2
1
x
y
Figure 4.3
Figure 4.4
cob19413_ch04_411-490.qxd 23/10/2008 01:51 PM Page 412 EPG 204:MHDQ069:mhcob%0:cob2ch04:
4-3 Section 4.1 One-to-One and Inverse Functions 413
EXAMPLE 1
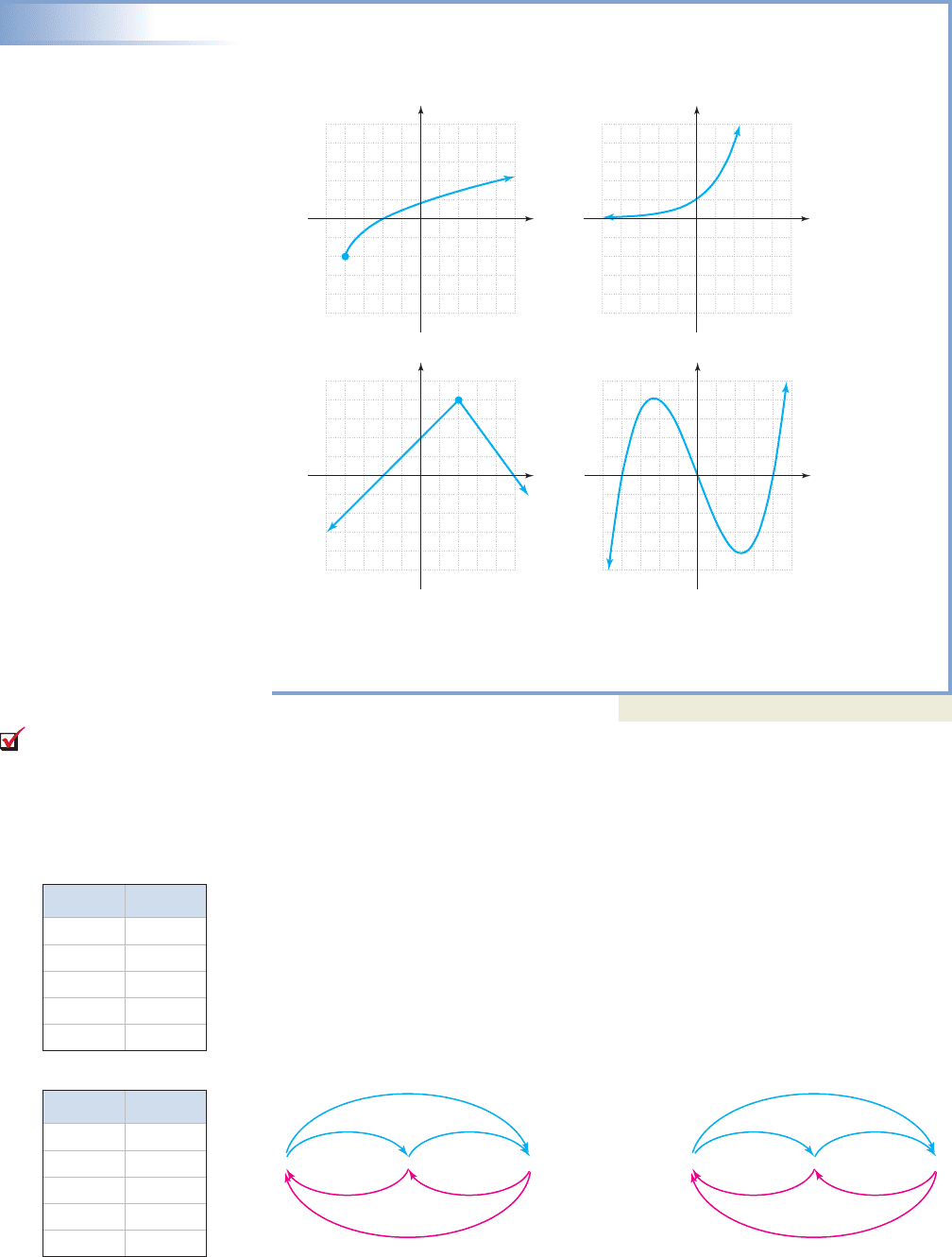
Identifying One-to-One Functions
Use the horizontal line test to determine whether each graph is the graph of a one-
to-one function.
a. b.
c. d.
Solution
A careful inspection shows all four graphs depict a function, since each passes the
vertical line test. Only (a) and (b) pass the horizontal line test and are one-to-one
functions.
Now try Exercises 7 through 28
If the function is given in ordered pair form, we simply check to see that no given
second coordinate is paired with more than one first coordinate.
B. Inverse Functions and Ordered Pairs
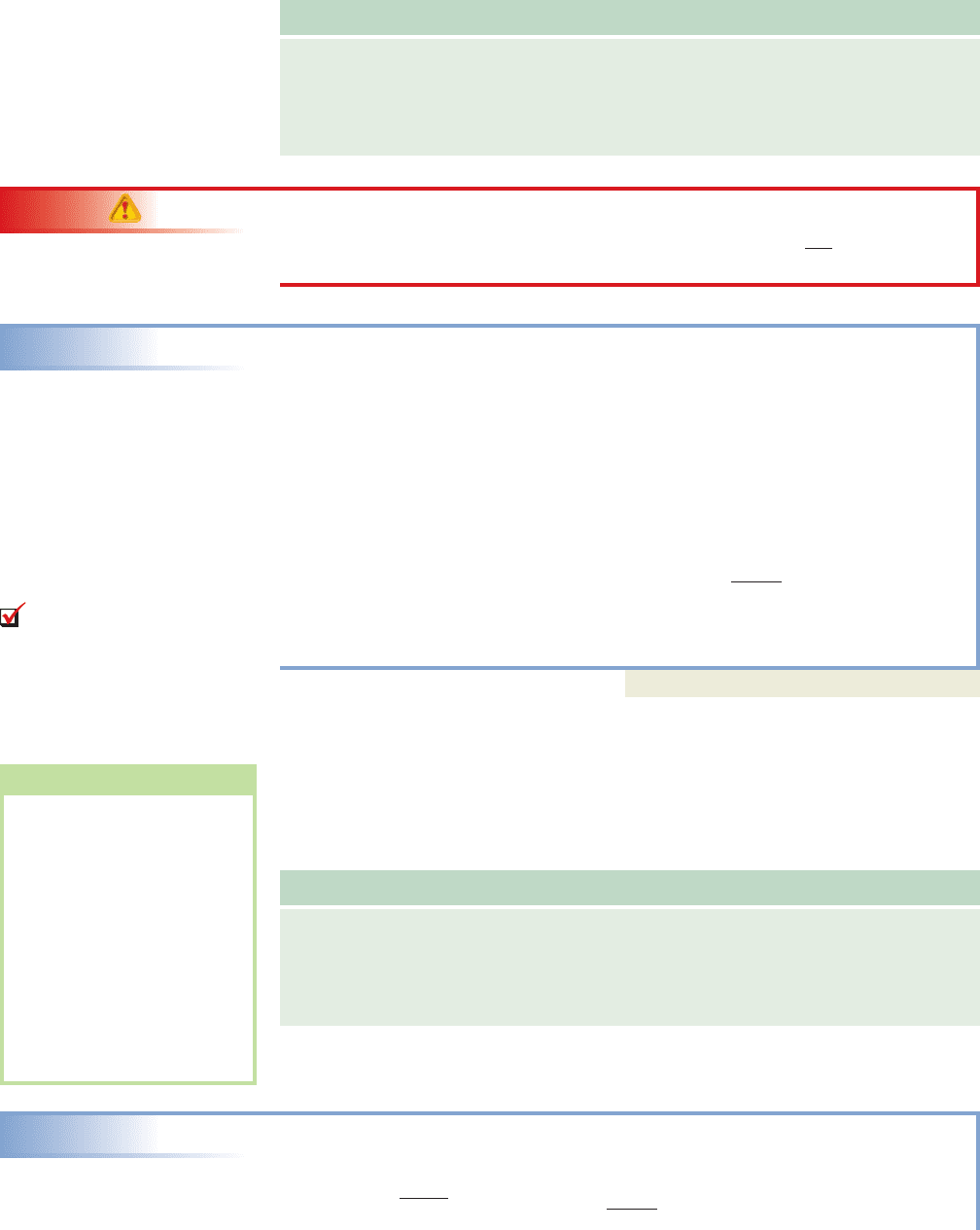
Consider the function and the solutions shown in Table 4.1. Figure 4.5
shows this function in diagram form (in blue), and illustrates that for each element of
the domain, we multiply by 2, then subtract 3. An inverse function for f is one that
takes the result of these operations (elements of the range), and returns the original
domain element. Figure 4.6 shows that function F achieves this by “undoing” the oper-
ations in reverse order: add 3, then divide by 2 (in red). A table of values for F(x) is
shown (Table 4.2).
f 1x2 2x 3
55
5
5
x
y
55
5
5
x
y
55
5
5
x
y
55
5
5
x
y
A. You’ve just learned
how to identify a one-to-one
function
x
2x
Multiply by 2
Divide by 2
Subtract 3
Add 3
y 2x 3
f
F
5 10
Multiply by 2
Divide by 2
Subtract 3
Add 3
7
f
F
Figure 4.5
Figure 4.6
xf(x)
0
21
57
813
3
93
Table 4.1
xF(x)
0
12
75
13 8
3
39
Table 4.2
cob19413_ch04_411-490.qxd 23/10/2008 01:51 PM Page 413 EPG 204:MHDQ069:mhcob%0:cob2ch04:
414 CHAPTER 4 Exponential and Logarithmic Functions 4-4
From this illustration we make the following observations regarding an inverse
function, which we actually denote as .
Inverse Functions
If f is a one-to-one function with ordered pairs (a, b),
1. is a one-to-one function with ordered pairs (b, a).
2. The range of f will be the domain of .
3. The domain of f will be the range of .
CAUTION
The notation is simply a way of denoting an inverse function and has nothing to
do with exponential properties. In particular, does not mean .
EXAMPLE 2
Finding the Inverse of a Function
Find the inverse of each one-to-one function given:
a.
b.
Solution
a. When a function is defined as a set of ordered pairs, the inverse function
is found by simply interchanging the x- and y-coordinates:
.
b. Using diagrams similar to Figures 4.5 and 4.6, we reason that will
subtract 2, then divide the result by . As a test, we find
that ( , 8), (0, 2), and (3, ) are solutions to p(x), and note that (8, ),
(2, 0), and ( , 3) are indeed solutions to .
Now try Exercises 29 through 40
C. Finding Inverse Functions Using an Algebraic Method
The fact that interchanging x- and y-values helps determine an inverse function can be
generalized to develop an algebraic method for finding inverses. Instead of inter-
changing specific x- and y-values, we actually interchange the x- and y-variables, then
solve the equation for y. The process is summarized here.
Finding an Inverse Function
1. Use y instead of f(x).
2. Interchange x and y.
3. Solve the equation for y.
4. The result gives the inverse function: substitute for y.
In this process, it might seem like we’re using the same y to represent two different
functions. To see why there is actually no contradiction, see Exercise 103.
EXAMPLE 3
Finding Inverse Functions Algebraically
Use the algebraic method to find the inverse function for
a. b. g1x2
2x
x 1
f 1x2 1
3
x 5
f
1
1x2
p
1
1x27
272
3: p
1
1x2
x 2
3
p
1
1x2
f
1
1x2 5113, 42, 17, 12, 15, 02, 11, 22, 15, 52, 111, 826
p1x23x 2
f 1x2 514, 132, 11, 72, 10, 52, 12, 12, 15, 52, 18, 1126
1
f1x2
f
1
1x2
f
1
1x2
f
1
1x2
f
1
1x2
f
1
1x2
f
1
1x2
WORTHY OF NOTE
If a function is not one-to-
one, no inverse function
exists since interchanging the
x- and y-coordinates will
result in a nonfunction. For
instance, interchanging the
coordinates of ( , 4) and
(2, 4) from results in
(4, ) and (4, 2), and we
have one x-value being
mapped to two y-values,
in violation of the function
definition.
2
y x
2
2
B. You’ve just learned how
to explore inverse functions
using ordered pairs
College Algebra—
cob19413_ch04_411-490.qxd 23/10/2008 01:51 PM Page 414 EPG 204:MHDQ069:mhcob%0:cob2ch04:
4-5 Section 4.1 One-to-One and Inverse Functions 415
Solution
a. given function
use y instead of f(x)
interchange x and y
cube both sides
solve for y
the result is
For
b.
given function
use y instead of f(x)
interchange x and y
multiply by and distribute
gather terms with y
factor
solve for y
the result is
For .
Now try Exercises 41 through 48
In cases where a given function is not one-to-one, we can sometimes restrict the
domain to create a function that is, and then determine an inverse. The restriction we use
is arbitrary, and only requires that the result still produce all possible range values. For
the most part, we simply choose a limited domain that seems convenient or reasonable.
EXAMPLE 4
Restricting the Domain to Create a One-to-One Function
Given , restrict the domain to create a one-to-one function, then
find . State the domain and range of both resulting functions.
Solution
The graph of f is a parabola, opening upward with the
vertex at (4, 0). Restricting the domain to
(see figure) leaves only the “right branch” of the
parabola, creating a one-to-one function without
affecting the range, . For ,
, we have
given function
use y instead of f(x)
interchange x and y
take square roots
solve for y, use since
The result shows , with domain and range
(the domain of f becomes the range of , and the range of f becomes
the domain of ).
Now try Exercises 49 through 54
f
1
f
1
y 34, q2
x 30, q2f
1
1x2 1x 4
x 41x 1x 4 y
1x
y 4
x 1y 42
2
y 1x 42
2
f 1x2 1x 42
2
x 4
f 1x2 1x 42
2
y 30, q2
x 4
f
1
1x2
f 1x2 1x 42
2
g1x2
2x
x 1
, g
1
1x2
x
2 x
g
1
1x2
x
2 x
g
1
1x2
x
2 x
y
x y12 x2
x 2y xy
y 1 xy x 2y
x
2y
y 1
y
2x
x 1
g1x2
2x
x 1
f 1x2 1
3
x 5, f
1
1x2 x
3
5.
f
1
1x2 x
3
5 f
1
1x2
x
3
5 y
x
3
y 5
x 1
3
y 5
y 1
3
x 5
f 1x2 1
3
x 5
5
5
5
x
y
College Algebra—
cob19413_ch04_411-490.qxd 25/10/2008 11:23 AM Page 415 EPG 204:MHDQ069:mhcob%0:cob2ch04:
416 CHAPTER 4 Exponential and Logarithmic Functions 4-6
While we now have the ability to find the inverse of a function, we still lack a defin-
itive method of verifying the inverse is correct. Actually, the diagrams in Figures 4.5
and 4.6 suggest just such a method. If we use the function f itself as an input for ,
or the function as an input for f, the end result should simply be x, as each func-
tion “undoes” the operations of the other. From Section 2.8 this is called a composi-
tion of functions and using the notation for composition we have,
Verifying Inverse Functions
If f is a one-to-one function, then the function exists, where
EXAMPLE 5
Finding and Verifying an Inverse Function
Use the algebraic method to find the inverse function for Then
verify the inverse you found is correct.
Solution
Since the graph of f is the graph of shifted 2 units left, we know f is one-
to-one with domain and range This is important since
the domain and range values will be interchanged for the inverse function. The
domain of will be and its range
given function;
use y instead of f(x)
interchange x and y
solve for y (square both sides)
subtract 2
the result is ; D: R:
Verify
is an input for f
f adds 2 to inputs, then takes the square root
substitute for
simplify
✓
since the domain of is )
Verify
f(x) is an input for
squares inputs, then subtracts 2
substitute for f(x)
simplify
✓
result
Now try Exercises 55 through 80
D. The Graph of a Function and Its Inverse
Graphing a function and its inverse on the same axes reveals an interesting and useful
relationship—the graphs are reflections across the line (the identity function).
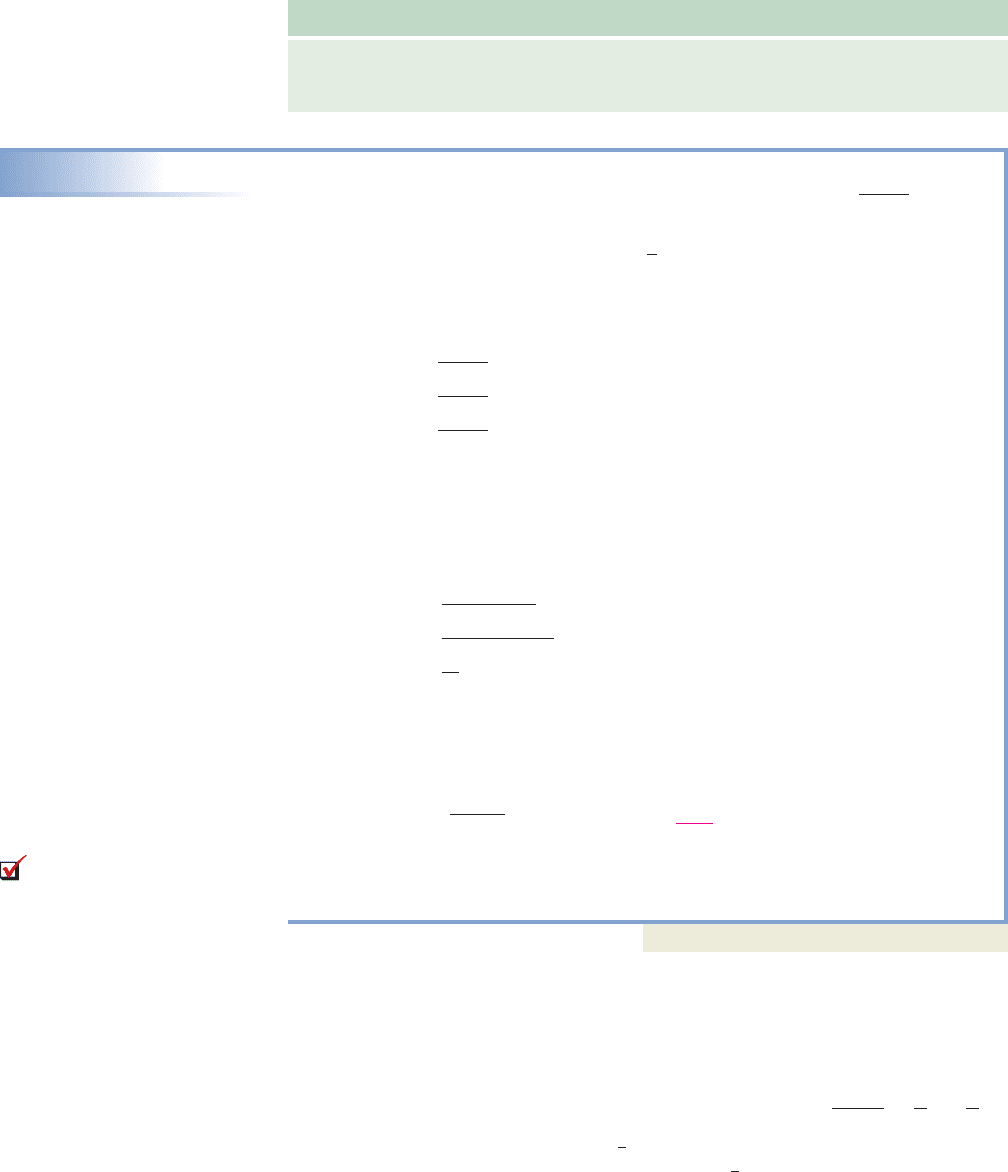
Consider the function , and its inverse . In
Figure 4.7, the points (1, 5), (0, 3), ( , 0), and ( ) from f (see Table 4.3) are
graphed in blue, with the points (5, 1), (3, 0), (0, ), and ( ) (see Table 4.4)5, 4
3
2
4, 5
3
2
f
1
1x2
x 3
2
1
2
x
3
2
f 1x2 2x 3
y x
x
x 2 2
1x 2 32 x 2 4
2
2
f
1
3f 1x24
2
2
f
1
1f
1
f 21x2 f
1
3f 1x24
x 30, qf
1
1x 2 x
2x
2
f
1
1x2x
2
2 21x
2
22 2
2f
1
1x2 2
f
1
1x 2 1f f
1
21x2 f 3f
1
1x24
y 32, q2x 30, q2,f
1
1x 2 f
1
1x2 x
2
2
x
2
2 y
x
2
y 2
x 1y 2
y 1x 2
x 2 f 1x2 1x 2
y 32, q2.x 30, q2f
1
y 30, q2.x 32, q2
y 1x
f 1x2 1x 2.
1f f
1
21x2 x
and
1f
1
f 21x2 x
f
1
f
1
f
1
C. You’ve just learned how
to find inverse functions using
an algebraic method
College Algebra—
cob19413_ch04_411-490.qxd 23/10/2008 01:51 PM Page 416 EPG 204:MHDQ069:mhcob%0:cob2ch04:
4-7 Section 4.1 One-to-One and Inverse Functions 417
from graphed in red (note the x- and y-values are reversed). Graphing both lines
illustrates this symmetry (Figure 4.8).
f
1
Figure 4.7Table 4.3
xf(x)
1
5
0
3
0
54
3
2
Table 4.4
xf
1
(x)
5
1
3
0
0
45
3
2
y x
f(x) 2x 3
542135 4 3 2 1
5
4
3
2
1
5
4
3
2
1
x
y
f
1
(x)
x 3
2
542135 4 3 2 1
5
4
3
2
1
5
4
3
2
1
x
y
y x
f(x) 2x 3
f
1
(x)
x 3
2
Figure 4.8
Figure 4.9 Figure 4.10
542135 4 3 2 1
5
4
3
2
1
5
4
3
2
1
x
y
f
1
(x) x
2
2
y x
f(x) x 2
542135 4 3 2 1
5
4
3
2
1
5
4
3
2
1
x
y
f
1
(x) x
2
2
y x
f(x) x 2
(2, 4)
(0, 1)
(1, 2)
f(x)
55
5
5
x
y
(4, 2)
(1, 0)
(2, 1)
f(x)
55
5
5
x
y
f
1
(x)
Figure 4.12Figure 4.11
College Algebra—
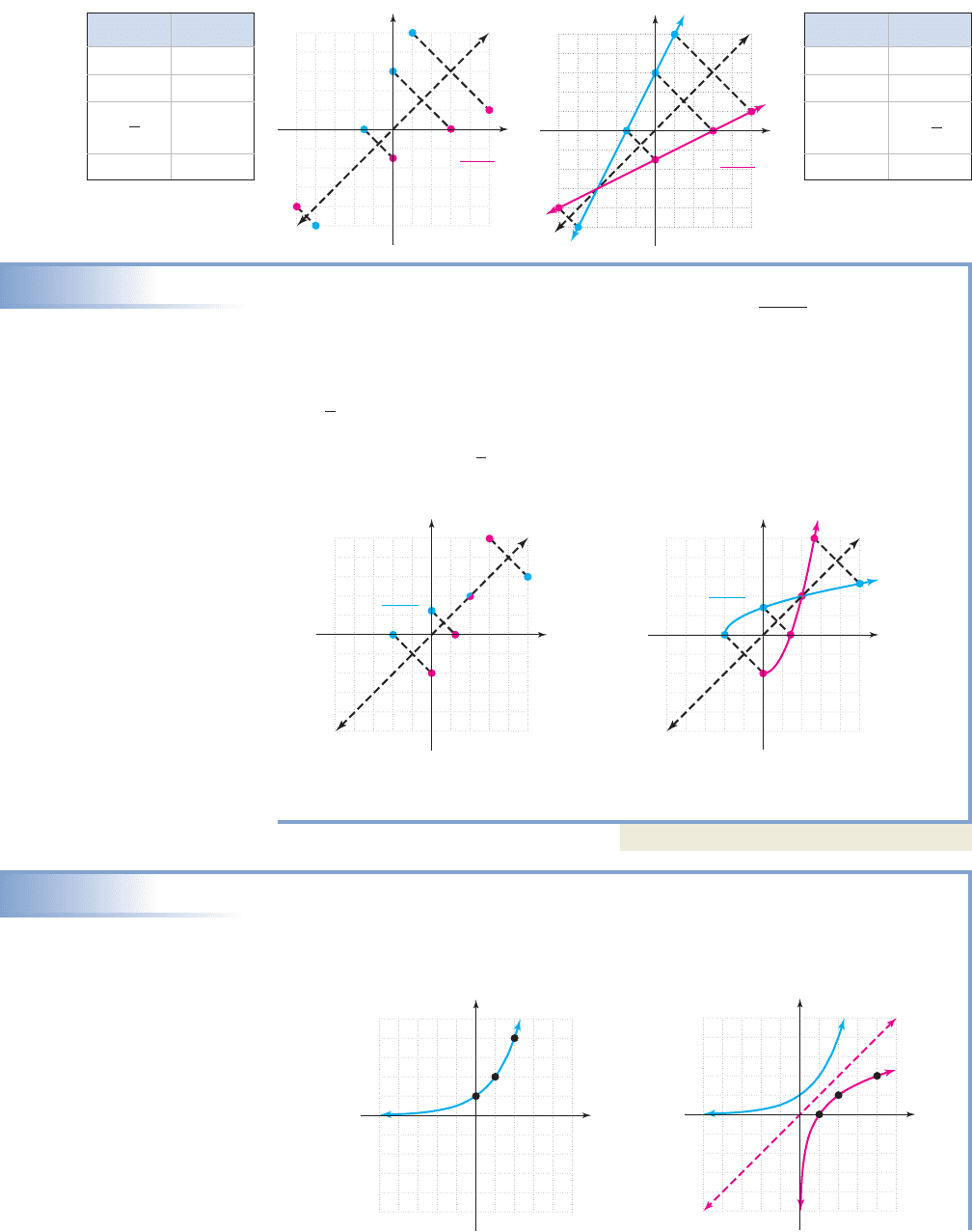
EXAMPLE 6
Graphing a Function and Its Inverse
In Example 5, we found the inverse function for was
Graph these functions on the same axes and comment on how the
graphs are related.
Solution
The graph of f is a square root function with initial point a y-intercept of
and an x-intercept of (Figure 4.9 in blue). The graph of
is the right-hand branch of a parabola, with y-intercept at
and an x-intercept at (Figure 4.9 in red).112
, 02
10, 22x
2
2, x 0
12, 0210, 12
2,
12, 02,
x
2
2, x 0.
f
1
1x2f 1x2 1x 2
Connecting these points with a smooth curve indeed shows their graphs are
symmetric to the line (Figure 4.10).
Now try Exercises 81 through 88
EXAMPLE 7
Graphing a Function and Its Inverse
Given the graph shown in Figure 4.11, use the grid in Figure 4.12 to draw a graph
of the inverse function.
y x
cob19413_ch04_411-490.qxd 23/10/2008 01:51 PM Page 417 EPG 204:MHDQ069:mhcob%0:cob2ch04:

418 CHAPTER 4 Exponential and Logarithmic Functions 4-8
Solution
From the graph, the domain of f appears to be and the range is
This means the domain of will be and the range will be To
sketch , draw the line interchange the x- and y-coordinates of the
selected points, then plot these points and draw a smooth curve using the domain
and range boundaries as a guide.
Now try Exercises 89 through 94
A summary of important points is given here followed by their application in Example 8.
Functions and Inverse Functions
1. If the graph of a function passes the horizontal line test, the function is
one-to-one.
2. If a function f is one-to-one, the function exists.
3. The domain of f is the range of , and the range of f is the domain of .
4. For a function f and its inverse , and
5. The graphs of f and are symmetric with respect to the line .
E. Applications of Inverse Functions
Our final example illustrates one of the many ways that inverse functions can be
applied.
EXAMPLE 8
Using Volume to Understand Inverse Functions
The volume of an equipoise cylinder (height equal to diameter)
is given by (since ), where v(x)
represents the volume in units cubed and x represents the radius
of the cylinder.
a. Find the volume of such a cylinder if
b. Find , and discuss what the input and output variables
represent.
c. If a volume of is required, which formula would be easier to use to
find the radius? What is this radius?
Solution
a. given function
substitute 10 for x
, exact form
With a radius of 10 ft, the volume of the cylinder would be .
b.
given function
use y instead of v(x)
interchange x and y
solve for y
result
The inverse function is . In this case, the input x is a given volume,
the output is the radius of an equipoise cylinder that will hold this volume.
v
1
1x2
v
1
1x2
A
3
x
2
B
3
x
2
y
x
2
y
3
x 2y
3
y 2x
3
v1x2 2x
3
2000 ft
3
10
3
1000 2000
v1102 21102
3
v1x2 2x
3
1024 ft
3
v
1
1x2
x 10 ft.
h d 2rv1x2 2x
3
y xf
1
1f
1
f 21x2 x.1f f
1
21x2 xf
1
f
1
f
1
f
1
y x,f
1
y .x 10, q2f
1
y 10, q2.x
D. You’ve just learned how
to graph a function and its
inverse
College Algebra—
cob19413_ch04_411-490.qxd 11/23/08 13:47 Page 418
4-9 Section 4.1 One-to-One and Inverse Functions 419
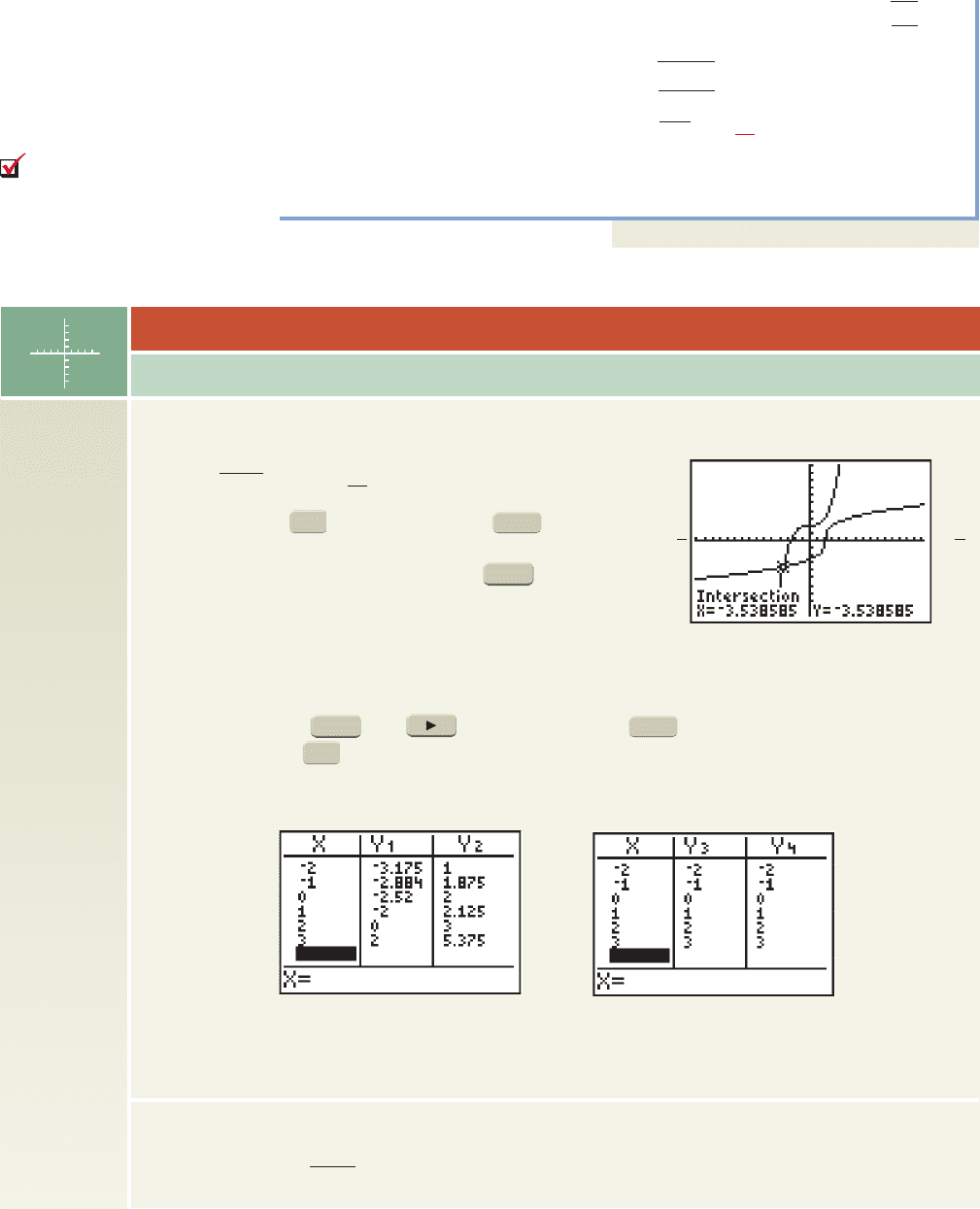
Investigating Inverse Functions
TECHNOLOGY HIGHLIGHT
Many important ideas from this section can be illustrated
using a graphing calculator. To begin, enter the function
and (which appear to be inverse
functions) on the screen, then press
5:ZSquare. The graphs seem to be reflections across the
line (Figure 4.13). To verify, use the feature
with inputs , 0, 1, 2, and 3. As shown in
Figure 4.14, the points (1, ), (2, 0), and (3, 2) are on Y
1
,
and the points ( , 1), (0, 2), and (2, 3) are all on Y
2
. While
this seems convincing (the x- and y-coordinates are interchanged), the technology can actually
compose the two functions to verify an inverse relationship. Function names Y
1
and Y
2
can be
accessed using the and keys, then pressing . After entering and
on the screen, we observe whether one function “undoes” the other using the
TABLE feature (Figure 4.15).
Y =
Y
4
Y
2
1Y
1
2
Y
3
Y
1
1Y
2
2
ENTER
VARS
2
2
x 2, 1
TABLE
y x
ZOOM
Y =
Y
2
x
3
8
2Y
1
22
3
x 2
10
10
15
5
31
15
5
31
c. Since the volume is known and we need the radius, using
would be more efficient.
substitute for x in
result
The radius of the cylinder would be 8 ft.
Now try Exercises 97 through 102
8
2
2
1 1
3
512
v
1
1x21024 v
1
110242
B
3
1024
2
v
1
1x2
A
3
x
2
Figure 4.13
Figure 4.14 Figure 4.15
College Algebra—
For the functions given, (a) find , then use your calculator to verify they are inverses by
(b) using ordered pairs, (c) composing the functions, and (d) showing their graphs are symmetric
to .
Exercise 1: Exercise 2:
Exercise 3: h1x2
x
x 1
g1x2 x
2
1; x 0f 1x2 2x 1
y x
f
1
1x2
E. You’ve just learned how
to solve an application of
inverse functions
cob19413_ch04_411-490.qxd 23/10/2008 01:51 PM Page 419 EPG 204:MHDQ069:mhcob%0:cob2ch04:
