Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.


190 CHAPTER 2 Relations, Functions, and Graphs 2-40
MAINTAINING YOUR SKILLS
116. (2.2) Determine the domain:
a.
b.
117.
(1.5) Solve using the quadratic formula. Answer in
exact and approximate form: .
118. (1.1) Three equations follow. One is an identity,
another is a contradiction, and a third has a
solution. State which is which.
21x 52 13 1 9 7 2x
21x 42 13 1 9 7 2x
21x 52 13 1 9 7 2x
3x
2
10x 9
y
5
2x
2
3x 2
y 12x 5
119. (R.7) Compute the area of the circular sidewalk
shown here. Use your calculator’s value of and
round the answer (only) to hundredths.
8 yd
10 yd
and y-intercept using the general form (solve for y).
Based on what you see, when does the intercept
method work most efficiently?.
115. Match the correct graph to the conditions stated for
m and b. There are more choices than graphs.
a. b.
c. d.
e. f.
g. h.
m 0, b 6 0m 7 0, b 0
m 6 0, b 0m 0, b 7 0
m 7 0, b 7 0m 6 0, b 7 0
m 7 0, b 6 0m 6 0, b 6 0
x
y
x
y
x
y
(4) (5) (6)
x
y
x
y
x
y
(1) (2) (3)
In this section we introduce one of the most central ideas in mathematics—the concept
of a function. Functions can model the cause-and-effect relationship that is so impor-
tant to using mathematics as a decision-making tool. In addition, the study will help
to unify and expand on many ideas that are already familiar.
A. Functions and Relations
There is a special type of relation that merits further attention. A function is a relation
where each element of the domain corresponds to exactly one element of the range. In
other words, for each first coordinate or input value, there is only one possible second
coordinate or output.
Functions
A function is a relation that pairs each element from the domain
with exactly one element from the range.
Learning Objectives
In Section 2.4 you will learn how to:
A. Distinguish the graph of
a function from that of a
relation
B. Determine the domain
and range of a function
C. Use function notation
and evaluate functions
D. Apply the rate-of-change
concept to nonlinear
functions
2.4 Functions, Function Notation, and the Graph of a Function
College Algebra—
cob19413_ch02_151-282.qxd 11/21/08 23:28 Page 190 User-S178 MAC-OSX_1:Users:user-s178:Desktop:Abhay_21/11/08_Dont-del:cob2ch02:
2-41 Section 2.4 Functions, Function Notation, and the Graph of a Function 191
If the relation is defined by a mapping, we need only check that each element of
the domain is mapped to exactly one element of the range. This is indeed the case for
the mapping from Figure 2.1 (page 152), where we saw that each person cor-
responded to only one birthday, and that it was impossible for one person to be born
on two different days. For the relation shown in Figure 2.6 (page 153), each
element of the domain except zero is paired with more than one element of the range.
The relation is not a function.
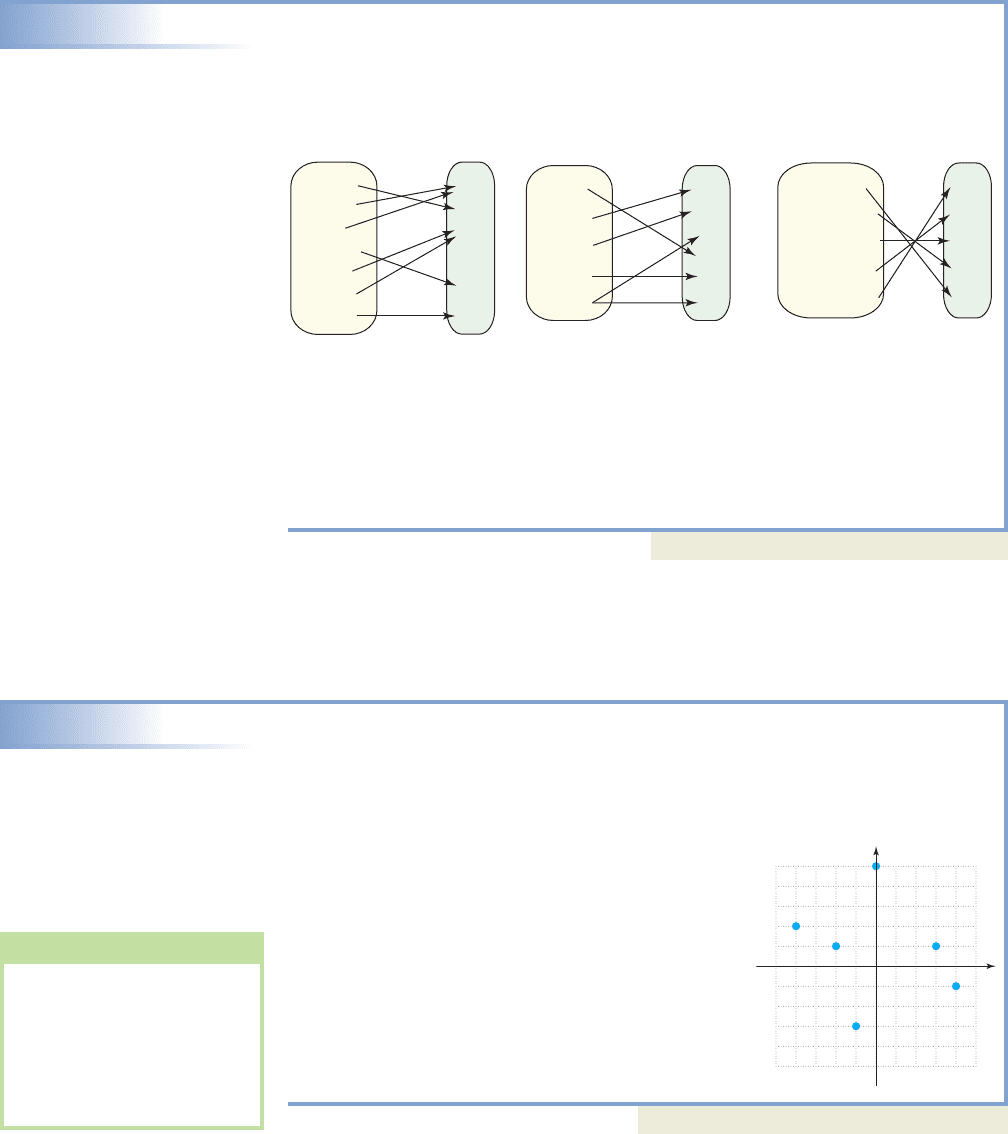
EXAMPLE 1
Determining Whether a Relation Is a Function
Three different relations are given in mapping notation below. Determine whether
each relation is a function.
a. b. c.
Solution
Relation (a) is a function, since each person corresponds to exactly one room. This
relation pairs math professors with their respective office numbers. Notice that
while two people can be in one office, it is impossible for one person to physically
be in two different offices. Relation (b) is not a function, since we cannot tell
whether Polly the Parrot weighs 2 lb or 3 lb (one element of the domain is mapped
to two elements of the range). Relation (c) is a function, where each major war is
paired with the year it began.
Now try Exercises 7 through 10
If the relation is defined by a set of ordered pairs or a set of individual and distinct
plotted points, we need only check that no two points have the same first coordinate
with a different second coordinate.
EXAMPLE 2
Identifying Functions
Two relations named f and g are given; f is stated as a set of ordered pairs, while g
is given as a set of plotted points. Determine whether each is a function.
( ), and (6, 1)
Solution
The relation f is not a function, since is paired
with two different outputs: ( and ( .
The relation g shown in the figure is a function.
Each input corresponds to exactly one output,
otherwise one point would be directly above the
other and have the same first coordinate.
Now try Exercises 11 through 18
3, 223, 02
3
4, 510, 12,f: 13, 02, 11, 42, 12, 52, 14, 22, 13, 22, 13, 62,
x
y
x
y
P S B
Marie
Pesky
Bo
Johnny
Rick
Annie
Reece
270
268
274
276
272
282
Person Room
Fido
Bossy
Silver
Frisky
Polly
450
550
2
40
8
3
Pet Weight (lbs)
War Year
Civil War
World War I
World War II
Korean War
Vietnam War
1963
1950
1939
1917
1861
College Algebra—
(4, 2)
(2, 1)
(1, 3)
(0, 5)
(4, 1)
(3, 1)
x
y
55
5
5
g
WORTHY OF NOTE
The definition of a function
can also be stated in ordered
pair form: A function is a set
of ordered pairs (x, y), in
which each first component
is paired with only one
second component.
cob19413_ch02_151-282.qxd 11/21/08 23:04 Page 191 User-S178 MAC-OSX_1:Users:user-s178:Desktop:Abhay_21/11/08_Dont-del:cob2ch02:
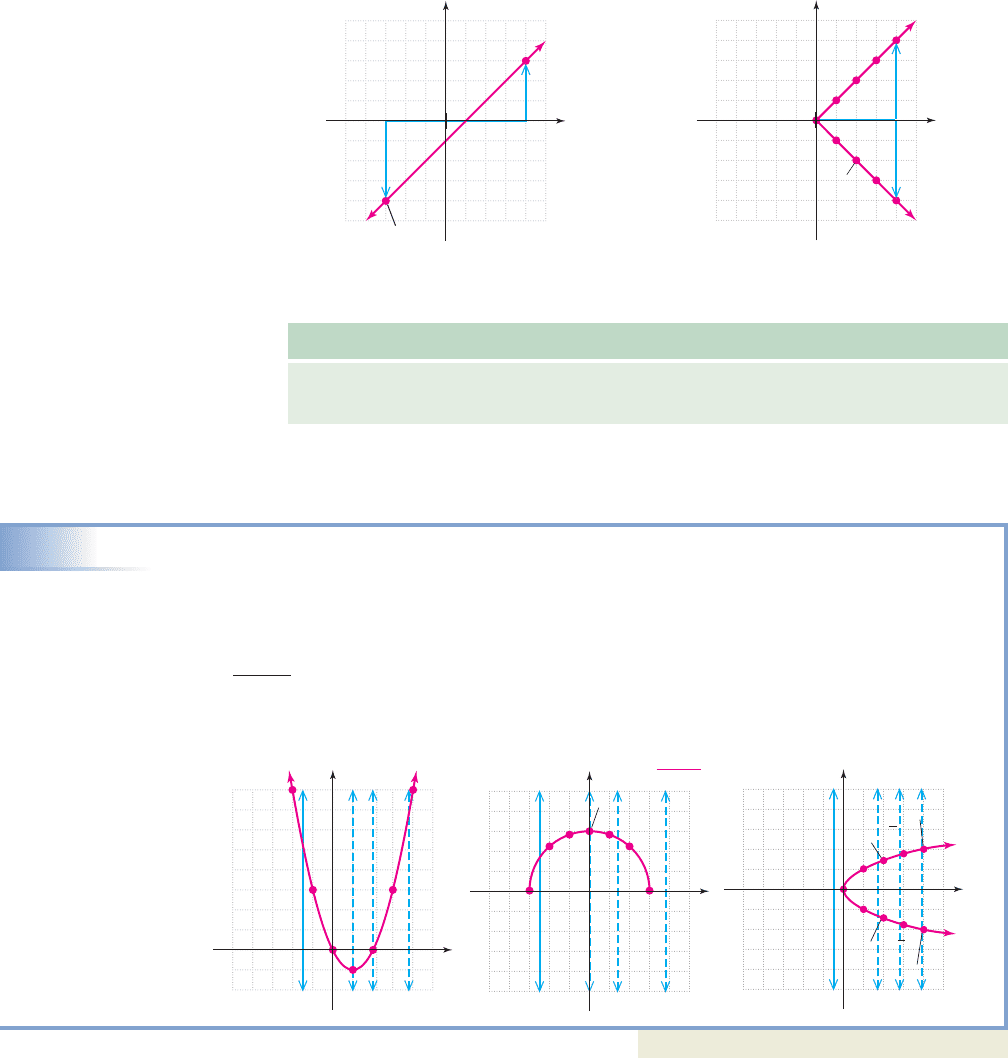
The graphs of and from Section 2.1 offer additional insight into
the definition of a function. Figure 2.23 shows the line with emphasis on
the plotted points (4, 3) and The vertical movement shown from the x-axis
to a point on the graph illustrates the pairing of a given x-value with one related
y-value. Note the vertical line shows only one related y-value ( is paired with
only ). Figure 2.24 gives the graph of highlighting the points (4, 4) and
(4, ). The vertical movement shown here branches in two directions, associating one
x-value with more than one y-value. This shows the relation is also a func-
tion, while the relation is not.
This “vertical connection” of a location on the x-axis to a point on the graph can
be generalized into a vertical line test for functions.
Vertical Line Test
A given graph is the graph of a function, if and only if every
vertical line intersects the graph in at most one point.
Applying the test to the graph in Figure 2.23 helps to illustrate that the graph of
any nonvertical line is a function.
EXAMPLE 3
Using the Vertical Line Test
Use the vertical line test to determine if any of the relations shown (from Section 2.1) are functions.
Solution
Visualize a vertical line on each coordinate grid (shown in solid blue), then mentally shift the
line to the left and right as shown in Figures 2.25, 2.26, and 2.27 (dashed lines). In Figures 2.25
and 2.26, every vertical line intersects the graph only once, indicating both and
are functions. In Figure 2.27, a vertical line intersects the graph twice for any
The relation is not a function.
Now try Exercises 19 through 30
x y
2
x 7 0.
y 29 x
2
y x
2
2x
x
y
y x 1
4
x
y
,y 3
x 4
13, 42.
y x 1
x
y
y x 1
(4, 3)
y x 1
(3, 4)
x
y
55
5
5
(2, 2)
(4, 4)
(0, 0)
(2, 2)
(4, 4)
x y
x
y
55
5
5
Figure 2.23
Figure 2.24
(2, 0)
(3, 3)
(2, 8)
(1, 3)
(0, 0)
(1, 1)
y x
2
2x
x
y
55
2
5
(4, 8)
(3, 0) (3, 0)
(0, 3)
y 9 x
2
x
y
55
5
5
(4, 2)
(2, 2)
(2, 2)
(4, 2)
y
2
x
x
y
55
(0, 0)
5
5
Figure 2.25 Figure 2.26 Figure 2.27
192 CHAPTER 2 Relations, Functions, and Graphs 2-42
College Algebra—College Algebra—
cob19413_ch02_151-282.qxd 11/21/08 23:05 Page 192 User-S178 MAC-OSX_1:Users:user-s178:Desktop:Abhay_21/11/08_Dont-del:cob2ch02:
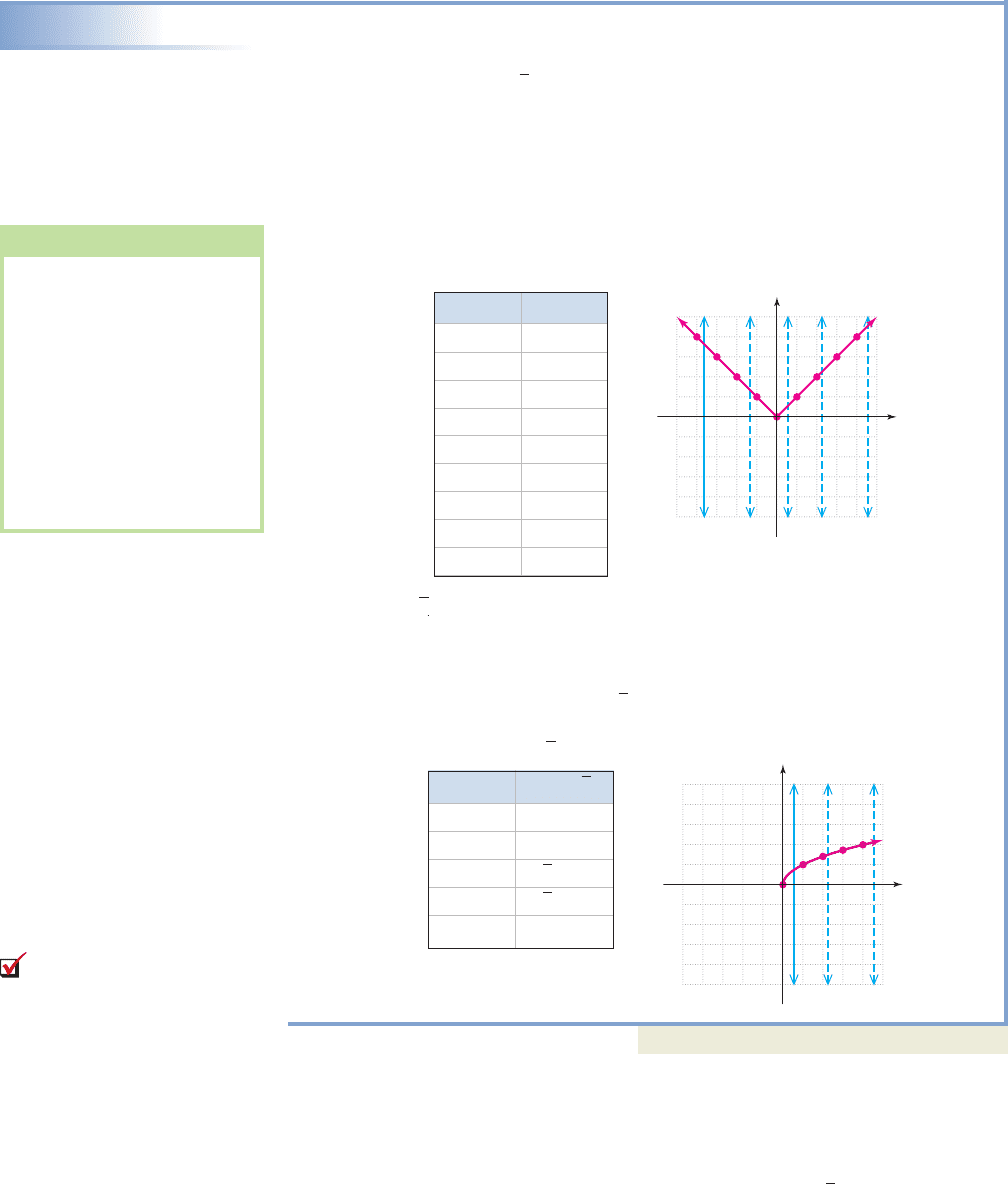
2-43 Section 2.4 Functions, Function Notation, and the Graph of a Function 193
EXAMPLE 4
Using the Vertical Line Test
Use a table of values to graph the relations defined by
a. b. ,
then use the vertical line test to determine whether each relation is a function.
Solution
a. For , using input values from to produces the following
table and graph (Figure 2.28). Note the result is a V-shaped graph that “opens
upward.” The point (0, 0) of this absolute value graph is called the vertex.
Since any vertical line will intersect the graph in at most one point, this is the
graph of a function.
b. For , values less than zero do not produce a real number, so our
graph actually begins at (0, 0) (see Figure 2.29). Completing the table for
nonnegative values produces the graph shown, which appears to rise to the
right and remains in the first quadrant. Since any vertical line will intersect this
graph in at most one place, is also a function.
Now try Exercises 31 through 34
B. The Domain and Range of a Function
Vertical Boundary Lines and the Domain
In addition to its use as a graphical test for functions, a vertical line can help determine
the domain of a function from its graph. For the graph of (Figure 2.29), a ver-
tical line will not intersect the graph until , and then will intersect the graph for all
values (showing the function is defined for these values). These vertical bound-
ary lines indicate the domain is . For the graph of (Figure 2.28), a ver-
tical line will intersect the graph (or its infinite extension) for all values of x, and the
y
x
x 30, q2
x 0
x 0
y 1x
y 1x
y 1x
x 4x 4y
x
y 1x
y
x
x
y
55
5
5
Figure 2.28
x
4
3
2
1
00
11
22
33
44
1
2
3
4
y x
y x
x
y
55
5
5
x
00
11
2
3
42
13
1.7
12
1.4
y 1x
y 1x
Figure 2.29
A. You’ve just learned how
to distinguish the graph of a
function from that of a relation
College Algebra—College Algebra—
WORTHY OF NOTE
For relations and functions, a
good way to view the dis-
tinction is to consider a mail
carrier. It is possible for the
carrier to put more than one
letter into the same mailbox
(more than one x going to
the same y), but quite impos-
sible for the carrier to place
the same letter in two
different boxes (one x going
to two y’s).
cob19413_ch02_151-282.qxd 11/21/08 23:05 Page 193 User-S178 MAC-OSX_1:Users:user-s178:Desktop:Abhay_21/11/08_Dont-del:cob2ch02:
194 CHAPTER 2 Relations, Functions, and Graphs 2-44
domain is . Using vertical lines in this way also affirms the domain of
(Section 2.1, Figure 2.5) is while the domain of the relation
(Section 2.1, Figure 2.6) is .
Range and Horizontal Boundary Lines
The range of a relation can be found using a horizontal “boundary line,” since it
will associate a value on the y-axis with a point on the graph (if it exists). Simply
visualize a horizontal line and move the line up or down until you determine the
graph will always intersect the line, or will no longer intersect the line. This will
give you the boundaries of the range. Mentally applying this idea to the graph of
(Figure 2.29) shows the range is Although shaped very differ-
ently, a horizontal boundary line shows the range of (Figure 2.28) is also
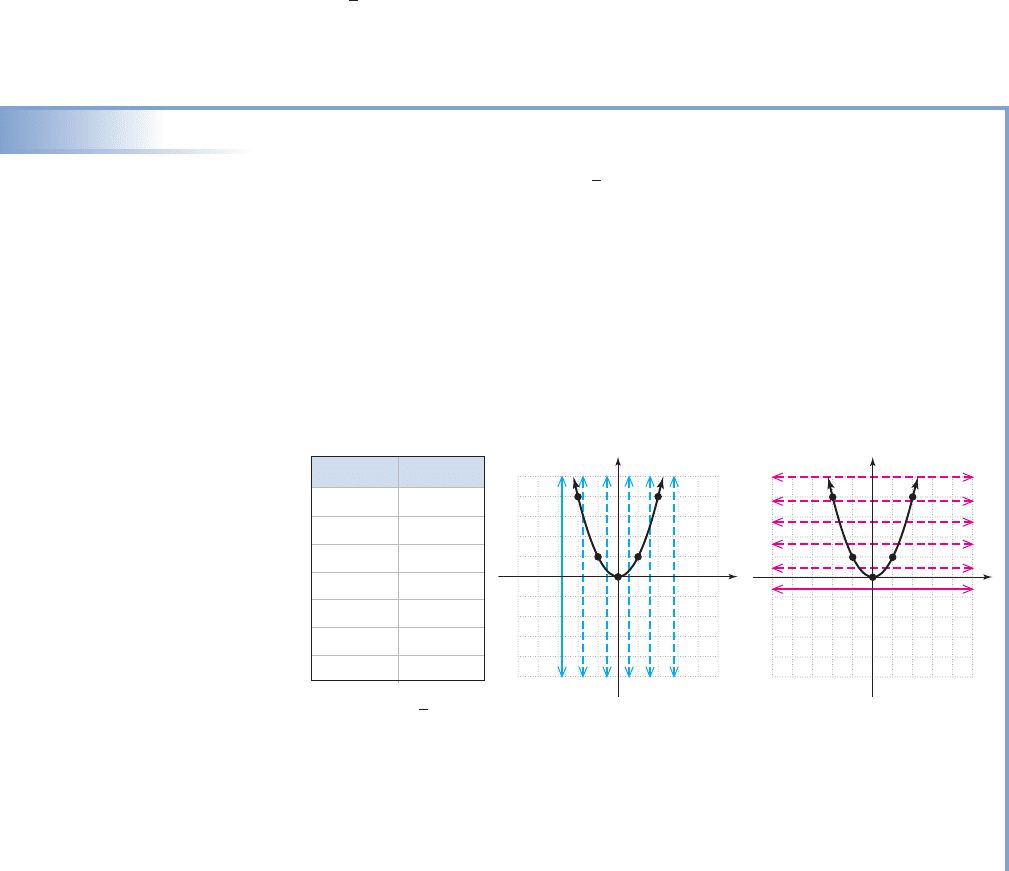
EXAMPLE 5
Determining the Domain and Range of a Function
Use a table of values to graph the functions defined by
a. b.
Then use boundary lines to determine the domain and range of each.
Solution
a. For , it seems convenient to use inputs from to ,
producing the following table and graph. Note the result is a basic parabola
that “opens upward” (both ends point in the positive y direction), with a vertex
at (0, 0). Figure 2.30 shows a vertical line will intersect the graph or its
extension anywhere it is placed. The domain is . Figure 2.31
shows a horizontal line will intersect the graph only for values of y that are
greater than or equal to 0. The range is .
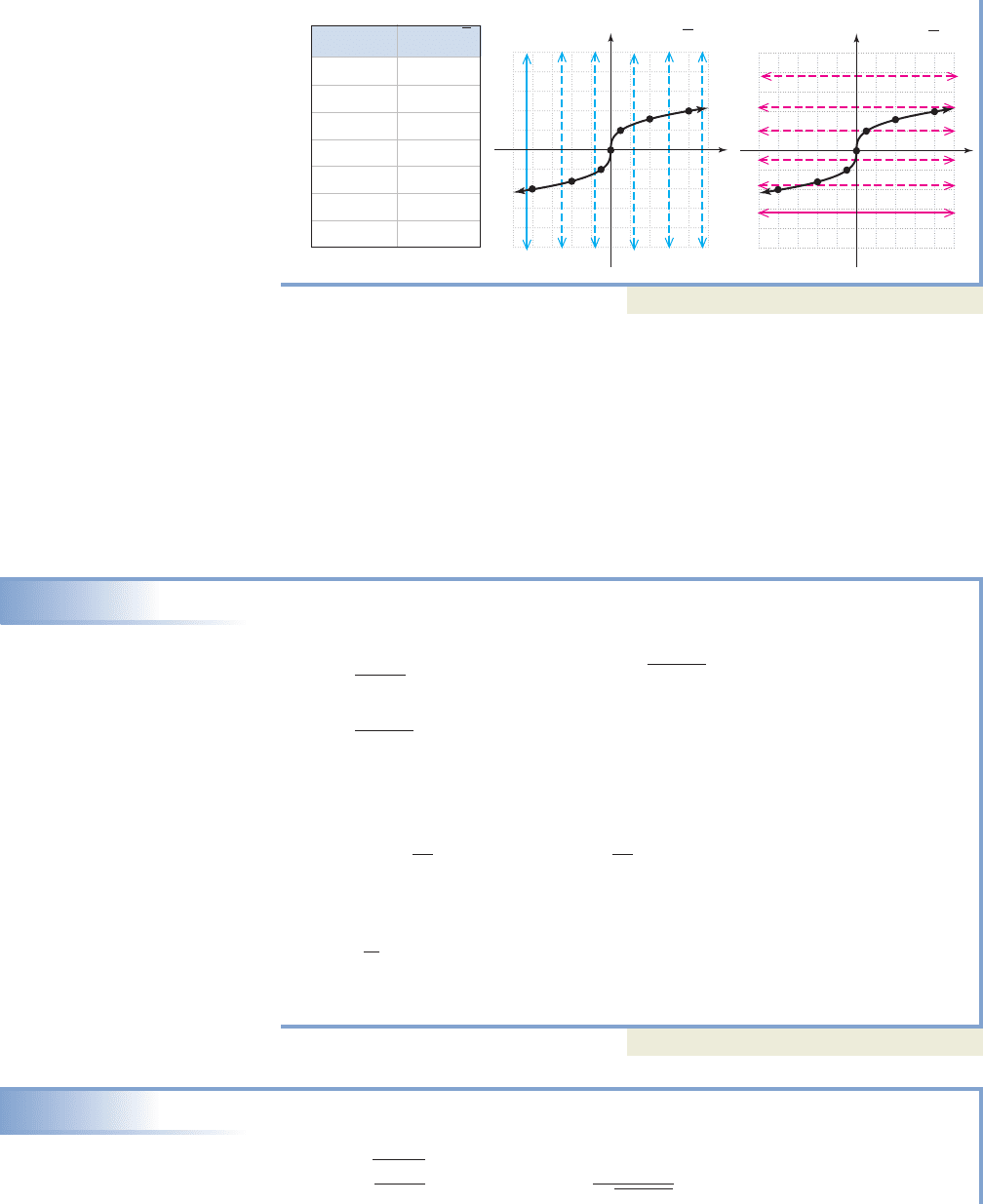
b. For , we select points that are perfect cubes where possible, then a few
others to round out the graph. The resulting table and graph are shown, and we
notice there is a “pivot point” at (0, 0) called a point of inflection, and the
ends of the graph point in opposite directions. Figure 2.32 shows a vertical line
will intersect the graph or its extension anywhere it is placed. Figure 2.33
shows a horizontal line will likewise always intersect the graph. The domain is
, and the range is .y 1q, q2x 1q, q2
y 1
3
x
y 30, q2
x 1
q, q2
x 3x 3y x
2
y 1
3
xy x
2
y 30, q2.
y
x
y 30, q2.y 1x
x 30, q2x
y
x 1q, q2y x 1
x 1q, q2
x
9
4
1
00
11
24
39
1
2
3
y x
2
Squaring Function
x
y
55
5
5
y x
2
x
y
55
5
5
y x
2
Figure 2.30
Figure 2.31
College Algebra—
cob19413_ch02_151-282.qxd 11/21/08 23:05 Page 194 User-S178 MAC-OSX_1:Users:user-s178:Desktop:Abhay_21/11/08_Dont-del:cob2ch02:
2-45 Section 2.4 Functions, Function Notation, and the Graph of a Function 195
Now try Exercises 35 through 46
Implied Domains
When stated in equation form, the domain of a function is implicitly given by the
expression used to define it, since the expression will dictate the allowable values
(Section 1.2). The implied domain is the set of all real numbers for which the func-
tion represents a real number. If the function involves a rational expression, the
domain will exclude any input that causes a denominator of zero. If the function
involves a square root expression, the domain will exclude inputs that create a nega-
tive radicand.
EXAMPLE 6
Determining Implied Domains
State the domain of each function using interval notation.
a. b.
c. d.
Solution
a. By inspection, we note an x-value of gives a zero denominator and must be
excluded. The domain is
b. Since the radicand must be nonnegative, we solve the inequality
giving The domain is
c. To prevent division by zero, inputs of and 3 must be excluded
(set and solve by factoring). The domain is
. Note that is in the domain
since is defined.
d. Since squaring a number and multiplying a number by a constant are defined
for all reals, the domain is
Now try Exercises 47 through 64
EXAMPLE 7
Determining Implied Domains
Determine the domain of each function:
a. b.
y
2x
14x 5
y
A
7
x 3
x 1q, q2.
0
16
0
x 5x 1q, 32 ´ 13, 32 ´ 13, q2
x
2
9 0
3
x 3
3
2
, q2.x
3
2
.
2x 3 0,
x 1q, 22 ´ 12, q2.
2
y x
2
5x 7y
x 5
x
2
9
y 12x 3
y
3
x 2
x
00
11
4
82
1.6
11
1.64
28
y 2
3
x
Cube Root Function
x
y
1010
5
5
y x
3
x
y
5
5
y x
3
10 10
Figure 2.32
Figure 2.33
College Algebra—
cob19413_ch02_191-206.qxd 11/22/08 20:38 Page 195
196 CHAPTER 2 Relations, Functions, and Graphs 2-46
Solution
a. For , we must have (for the radicand) and
(for the denominator). Since the numerator is always positive, we need
, which gives . The domain is .
b. For , we must have and . This indicates
or
.
The domain is
.
Now try Exercises 65 through 68
C. Function Notation
In our study of functions, you’ve likely noticed that the relationship between input and
output values is an important one. To highlight this fact, think of a function as a simple
machine, which can process inputs using a stated sequence of operations, then deliver
a single output. The inputs are x-values, a program we’ll name f performs the opera-
tions on x, and y is the resulting output (see Figure 2.34). Once again we see that “the
value of y depends on the value of x,” or simply “y is a function of x.” Notationally, we
write “y is a function of x” as using function notation.You are already famil-
iar with letting a variable represent a number. Here we do something quite different,
as the letter f is used to represent a sequence of operations to be performed on x. Con-
sider the function which we’ll now write as [since ].
In words the function says, “divide inputs by 2, then add 1.” To evaluate the function
at (Figure 2.35) we have:
input 4 input 4
Instead of saying, “. . . when the value of the function is 3,” we simply
say “f of 4 is 3,” or write Note that the ordered pair (4, 3) is equivalent to
(4, f(4)).
CAUTION
Although f(x) is the favored notation for a “function of x,” other letters can also be used.
For example, g(x) and h(x) also denote functions of x, where g and h represent a differ-
ent sequence of operations on the x-inputs. It is also important to remember that these
represent function values and not the product of two variables:
EXAMPLE 8
Evaluating a Function
Given find
a. b. c. d. f 1a 12f 12a2f a
3
2
bf 122
f 1x22x
2
4x,
f1x2 f
#
1x2.
f142 3.
x 4,
3
2 1
f142
4
2
1
f1x2
x
2
1
x 4
y f1x2f1x2
x
2
1y
x
2
1,
y f1x2
x 1
5
4
, q2x 7
5
4
4x 5 7 0
14x 5
04x 5 0y
2x
14x 5
x 13, q2x 7 3x 3 7 0
x 3 0
7
x 3
0y
A
7
x 3
Output
Sequence of
operations
on x as defined
by f(x)
y
f
Input
x
Figure 2.34
Output
Input
4
Divide
inputs by 2
then add 1
+ 1
2
4
3
f(x)
Figure 2.35
College Algebra—
↓
↓
B. You’ve just learned how
to determine the domain and
range of a function
cob19413_ch02_191-206.qxd 12/12/08 7:40 PM Page 196 epg HD 049:Desktop Folder:Satya 12/12/08:

2-47 Section 2.4 Functions, Function Notation, and the Graph of a Function 197
Solution
a.
c.
Now try Exercises 69 through 84
Graphs are an important part of studying functions, and learning to read and
interpret them correctly is a high priority. A graph highlights and emphasizes the all-
important input/output relationship that defines a function. In this study, we hope to
firmly establish that the following statements are synonymous:
1.
2.
3. is on the graph of f, and
4. When
EXAMPLE 9A
Reading a Graph
For the functions f(x) and g(x) whose graphs are shown in Figures 2.36 and 2.37
a. State the domain of the function.
b. Evaluate the function at .
c. Determine the value(s) of x for which y 3.
d. State the range of the function.
Solution
For f(x),
a. The graph is a continuous line segment with endpoints at ( ) and (5, 3),
so we state the domain in interval notation. Using a vertical boundary line we
note the smallest input is and the largest is 5. The domain is
b. The graph shows an input of corresponds to since (2, 1)
is a point on the graph.
c. For (or ) the input value must be since (5, 3) is the point
on the graph.
d. Using a horizontal boundary line, the smallest output value is and the
largest is 3. The range is y 33, 34.
3
x 5y 3f 1x2 3
y 1: f 122 1x 2
x 34, 54.4
4, 3
x 2
x 2, f1x2 5
12, 52
12, f 1222 12, 52
f122 5
8a
2
8a
214a
2
2 8a
f 12a2212a2
2
412a2
f 1x22x
2
4x
8 18216
f 1222122
2
4122
f 1x22x
2
4x
b.
d.
2a
2
2
2a
2
4a 2 4a 4
21a
2
2a 12 4a 4
f 1a 1221a 12
2
41a 12
f 1x22x
2
4x
9
2
6
3
2
f a
3
2
b2a
3
2
b
2
4a
3
2
b
f 1x22x
2
4x
Figure 2.36 Figure 2.37
f(x)
x
y
543215 4 3 2 1
1
2
3
2
3
4
5
1
g(x)
x
y
543215 4 3 2 1
1
2
3
2
3
4
5
1
College Algebra—
cob19413_ch02_191-206.qxd 12/12/08 7:57 PM Page 197 epg HD 049:Desktop Folder:Satya 12/12/08:
198 CHAPTER 2 Relations, Functions, and Graphs 2-48
For g(x),
a. Since the graph is pointwise defined, we state the domain as the set of first
coordinates:
b. An input of corresponds to since (2, 2) is on the graph.
c. For (or the input value must be since (4, 3) is a point
on the graph.
d. The range is the set of all second coordinates:
EXAMPLE 9B
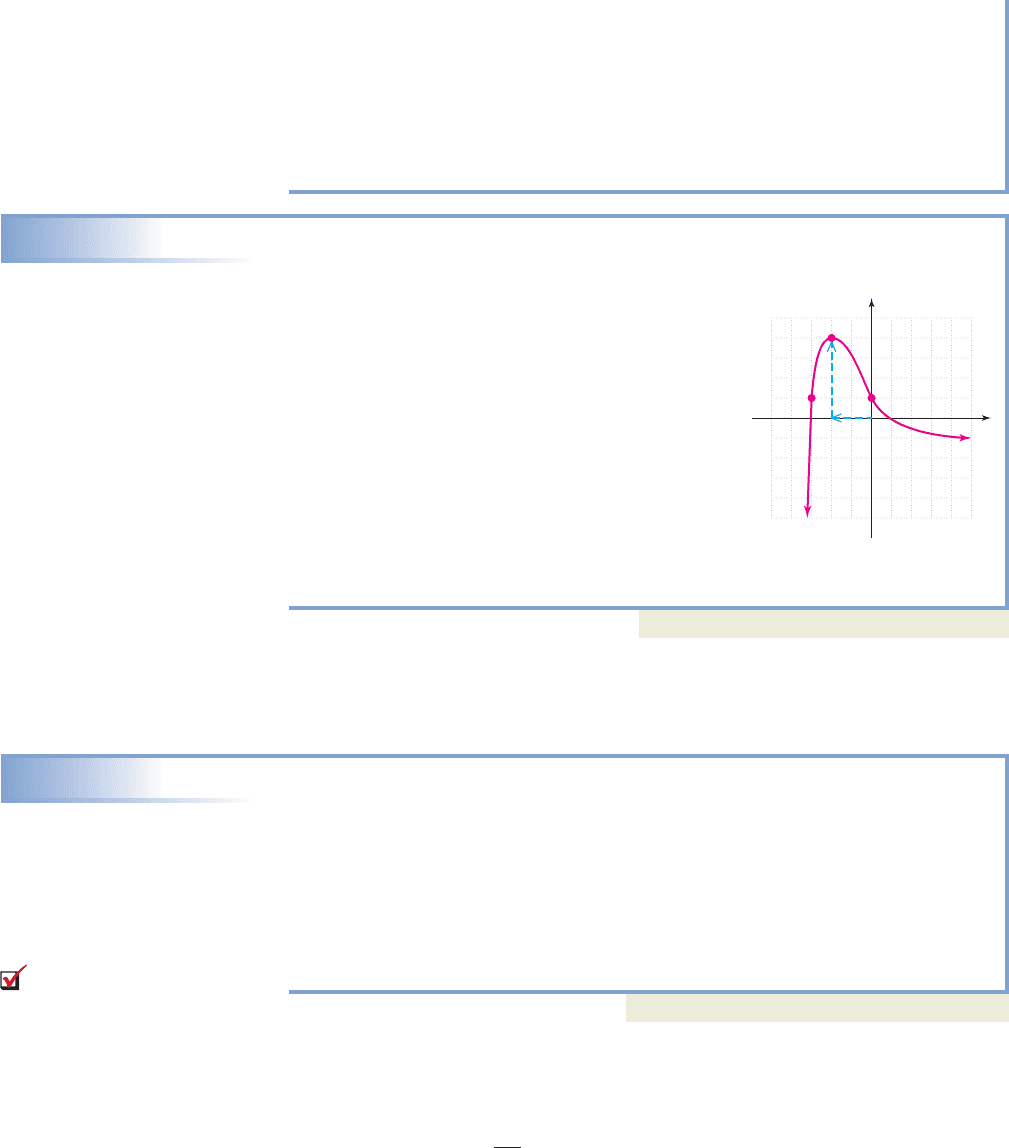
Reading a Graph
Use the graph of given to answer the following questions:
a. What is the value of ?
b. What value(s) of x satisfy ?
Solution
a. The notation says to find the value of the
function f when . Expressed graphically,
we go to , locate the corresponding point
on the graph of f (blue arrows), and find that
.
b. For , we’re looking for x-inputs that
result in an output of .
From the graph, we note there are two points
with a y-coordinate of 1, namely, ( , 1) and (0, 1). This shows
, and the required x-values are and .
Now try Exercises 85 through 90
In many applications involving functions, the domain and range can be determined
by the context or situation given.
EXAMPLE 10
Determining the Domain and Range from the Context
Paul’s 1993 Voyager has a 20-gal tank and gets 18 mpg. The number of miles he
can drive (his range) depends on how much gas is in the tank. As a function we
have where M(g) represents the total distance in miles and g
represents the gallons of gas in the tank. Find the domain and range.
Solution
Begin evaluating at since the tank cannot hold less than zero gallons. On a
full tank the maximum range of the van is or .
Because of the tank’s size, the domain is
Now try Exercises 94 through 101
D. Average Rates of Change
As noted in Section 2.3, one of the defining characteristics of a linear function is that
the rate of change is constant. For nonlinear functions the rate of change is
not constant, but we can use a related concept called the average rate of change to
study these functions.
m
¢y
¢x
g 30, 204.
M1g2 30, 360420
#
18 360 miles
x 0,
M1g2 18g,
x 0x 3f132 1, f102 1
3
3since y f1x24y 1
f1x2 1
f122 4
x 2
x 2
f122
f1x2 1
f122
f1x2
R 51, 0, 1, 2, 36.
x 4,y 32g1
x2 3
y 2: g122 2x 2
D 54, 2, 0, 2, 46.
C. You’ve just learned how
to use function notation and
evaluate functions
(2, 4)
(3, 1)
(0, 1)
y
55
5
5
x
f(x)
College Algebra—
cob19413_ch02_151-282.qxd 11/21/08 23:07 Page 198 User-S178 MAC-OSX_1:Users:user-s178:Desktop:Abhay_21/11/08_Dont-del:cob2ch02:
2-49 Section 2.4 Functions, Function Notation, and the Graph of a Function 199
Average Rate of Change
For a function that is smooth and continuous on the interval containing x
1
and x
2
, the
average rate of change between x
1
and x
2
is given by
which is the slope of the secant line through (x
1
, y
1
) and (x
2
, y
2
)
EXAMPLE 11
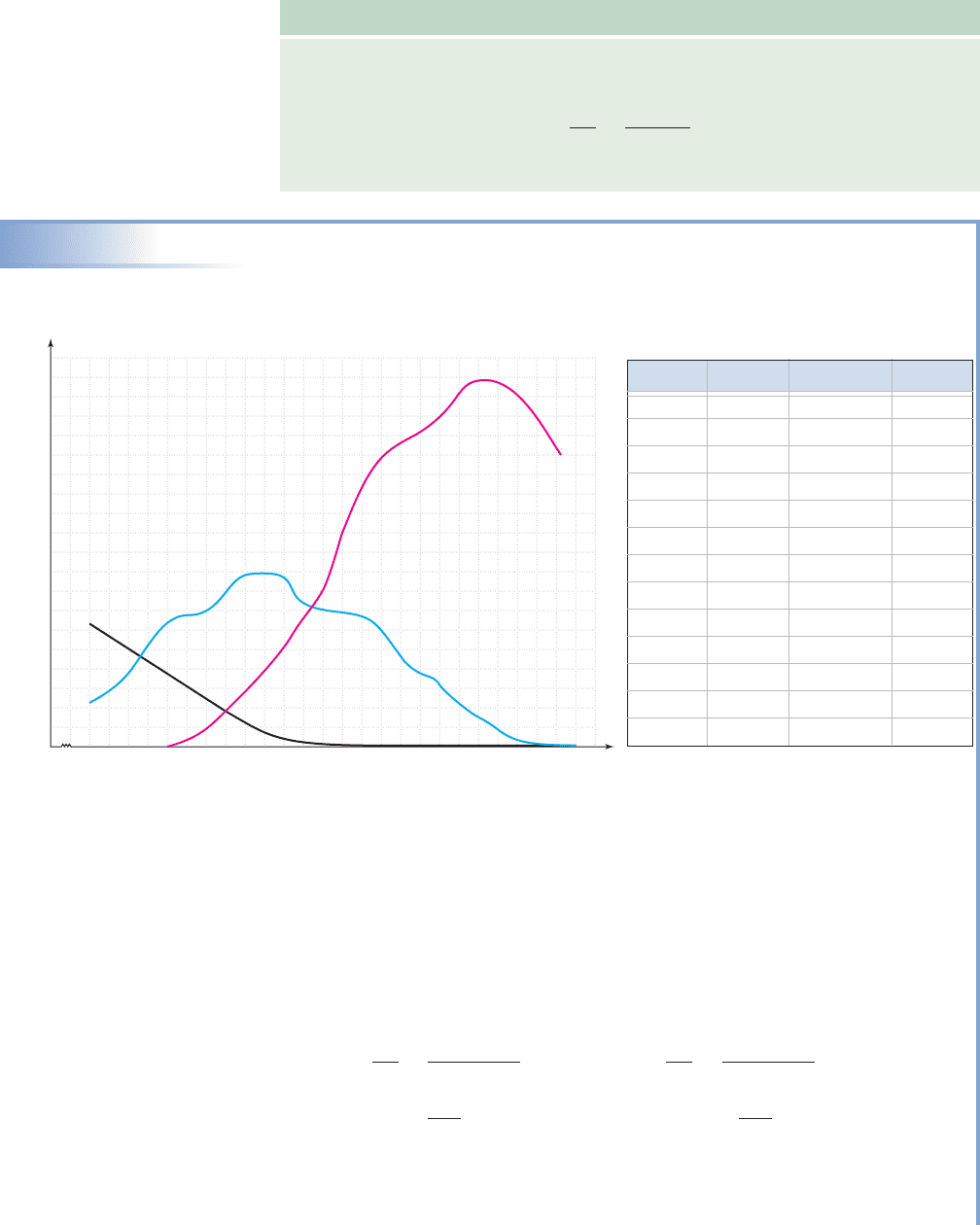
Calculating Average Rates of Change
The graph shown displays the number of units shipped of vinyl records, cassette
tapes, and CDs for the period 1980 to 2005.
a. Find the average rate of change in CDs shipped and in cassettes shipped from
1994 to 1998. What do you notice?
b. Does it appear that the rate of increase in CDs shipped was greater from 1986
to 1992, or from 1992 to 1996? Compute the average rate of change for each
period and comment on what you find.
Solution
Using 1980 as year zero ( ), we have the following:
a. CDs Cassettes
The decrease in the number of cassettes shipped was roughly equal to the
increase in the number of CDs shipped (about 46,000,000 per year).
46.5 46.25
186
4
185
4
¢y
¢x
159 345
18 14
¢y
¢x
847 662
18 14
1994: 114, 3452, 1998: 118, 15921994: 114, 6622, 1998: 118, 8472
1980 S 0
¢y
¢x
y
2
y
1
x
2
x
1
Year Vinyl Cassette CDs
1980 323 110 0
1982 244 182 0
1984 205 332 6
1986 125 345 53
1988 72 450 150
1990 12 442 287
1992 2 366 408
1994 2 345 662
1996 3 225 779
1998 3 159 847
2000 2 76 942
2004 1 5 767
2005 1 3 705
Units shipped in millions
80
100
200
300
400
1000
82 84
Units shipped (millions)
86 88 90
Cassettes
Vinyl
CDs
92 94 96 98 100 102 104 106
500
600
700
800
900
Year (80 → 1980)
College Algebra—
Source: Swivel.com
cob19413_ch02_151-282.qxd 11/21/08 23:08 Page 199 User-S178 MAC-OSX_1:Users:user-s178:Desktop:Abhay_21/11/08_Dont-del:cob2ch02:
