Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.

A-4 Appendix II More on Matrices
The Determinant of a General Matrix
To compute the determinant of a general square matrix, we introduce the idea of a
cofactor. For an matrix A, is the cofactor of matrix element
a
ij
, where represents the determinant of the corresponding minor matrix. Note that
is the sum of the row and column of the entry, and if this sum is even,
while if the sum is odd, (this is how the sign table for a
determinant was generated). To compute the determinant of an matrix,
multiply each element in any row or column by its cofactor and add. The result is a
tier-like process in which the determinant of a larger matrix requires computing the
determinant of smaller matrices. In the case of a matrix, each of the minor matri-
ces will be size , whose determinant then requires the computation of other
determinants. In the following illustration, two of the entries in the first row are zero
for convenience. For
Computing the first determinant gives , the second determinant is 14.
This gives:
74
det1A221162 31142
3 3163 3
we have: det1A22
#
112
11
†
202
14 1
32 1
† 132
#
112
13
†
122
3 11
0 31
†
A ≥
2030
1202
3 14 1
0 32 1
¥,
2 23 3
4 4
n n3 3
112
ij
1112
ij
1,
i j
M
ij
A
ij
112
ij
M
ij
n n
College Algebra and Trigonometry—
cob19529_app_A1-A14.qxd 01/02/2009 08:03 PM Page A-4 ssen 1 HD 506:broker:MHDQ092-APP:

The Equation of an Ellipse
In Section 10.2, the equation was devel-
oped using the distance formula and the definition of an ellipse. To find the standard
form of the equation, we treat this result as a radical equation, isolating one of the rad-
icals and squaring both sides.
isolate one radical
square both sides
We continue by simplifying the equation, isolating the remaining radical, and squar-
ing again.
simplify
isolate radical; divide by 4
square both sides
expand and distribute a
2
on left
add 2a
2
cx and rewrite equation
factor
divide by
Since , we know and . For convenience, we let
and it also follows that and (since ). Substituting
b
2
for we obtain the standard form of the equation of an ellipse (major axis
horizontal, since we stipulated ): . Note once again the x-intercepts
are ( , 0), while the y-intercepts are (0, ).
The Equation of a Hyperbola
Similar to the development of the equation of an ellipse, the equation
ba
x
2
a
2
y
2
b
2
1a 7 b
a
2
c
2
c 7 0a 7 ba
2
7 b
2
b
2
a
2
c
2
a
2
c
2
7 0a
2
7 c
2
a 7 c
a
2
1a
2
c
2
2
x
2
a
2
y
2
a
2
c
2
1
x
2
1a
2
c
2
2 a
2
y
2
a
2
1a
2
c
2
2
a
2
x
2
c
2
x
2
a
2
y
2
a
4
a
2
c
2
a
2
x
2
2a
2
cx a
2
c
2
a
2
y
2
a
4
2a
2
cx c
2
x
2
a
2
31x c2
2
y
2
4 a
4
2a
2
cx c
2
x
2
a21x c2
2
y
2
a
2
cx
4 cx 4a
2
4a21x c2
2
y
2
x
2
2cx c
2
y
2
4a
2
4a21x c2
2
y
2
x
2
2cx c
2
y
2
1x c2
2
y
2
4a
2
4a21x c2
2
y
2
1x c2
2
y
2
21x c2
2
y
2
2a 21x c2
2
y
2
21x c2
2
y
2
21x c2
2
y
2
2a
Deriving the Equation of a Conic
expand
binomials
expand
binomials
A-5
APPENDIX III
College Algebra and Trigonometry—
could have been developed using the
distance formula and the definition of a hyperbola. To find the standard form of this
equation, we apply the same procedures as before.
isolate one radical
square both sides
simplify
isolate radical; divide by 4
square both sides
expand and distribute a
2
on the right
add 2a
2
cx and rewrite equation
factor
divide by a
2
1c
2
a
2
2
x
2
a
2
y
2
c
2
a
2
1
x
2
1c
2
a
2
2 a
2
y
2
a
2
1c
2
a
2
2
c
2
x
2
a
2
x
2
a
2
y
2
a
2
c
2
a
4
c
2
x
2
2a
2
cx a
4
a
2
x
2
2a
2
cx a
2
c
2
a
2
y
2
c
2
x
2
2a
2
cx a
4
a
2
31x c2
2
y
2
4
cx a
2
a21x c2
2
y
2
4 cx 4a
2
4a21x c2
2
y
2
x
2
2cx c
2
y
2
4a
2
4a21x c2
2
y
2
x
2
2cx c
2
y
2
1x c2
2
y
2
4a
2
4a21x c2
2
y
2
1x c2
2
y
2
21x c2
2
y
2
2a 21x c2
2
y
2
21x c2
2
y
2
2a21x c2
2
y
2
cob19529_app_A1-A14.qxd 01/15/2009 04:01 PM Page A-5
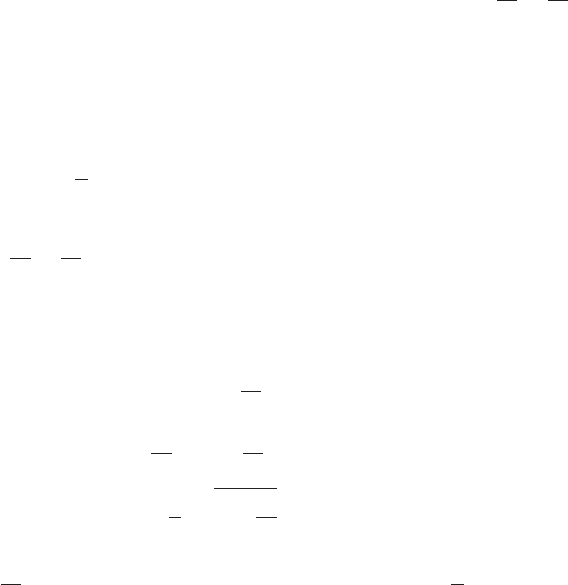
A-6 Appendix III Deriving the Equation of a Conic
From the definition of a hyperbola we have , showing and
. For convenience, we let and substitute to obtain the stan-
dard form of the equation of a hyperbola (transverse axis horizontal): .
Note the x-intercepts are (0, ) and there are no y-intercepts.
The Asymptotes of a Central Hyperbola
From our work in Section 10.3, a central hyperbola with a horizontal axis will have
asymptotes at . To understand why, recall that for asymptotic behavior we
investigate what happens to the relation for large values of x, meaning as .
Starting with , we have
clear denominators
isolate term with y
factor out b
2
x
2
from right side
divide by a
2
square root both sides
As , and we find that for large values of x, .y
b
a
x
x
Sq,
a
2
x
2
S 0
y
b
a
x
B
1
a
2
x
2
y
2
b
2
a
2
x
2
a1
a
2
x
2
b
a
2
y
2
b
2
x
2
a1
a
2
x
2
b
a
2
y
2
b
2
x
2
a
2
b
2
b
2
x
2
a
2
y
2
a
2
b
2
x
2
a
2
y
2
b
2
1
x
Sq
y
b
a
x
a
x
2
a
2
y
2
b
2
1
b
2
c
2
a
2
c
2
a
2
7 0
c
2
7 a
2
0 6 a 6 c
College Algebra and Trigonometry—
cob19529_app_A1-A14.qxd 01/02/2009 08:03 PM Page A-6 ssen 1 HD 506:broker:MHDQ092-APP:

Proofs from Chapter 3
The Remainder Theorem
If a polynomial p(x) is divided by ( ) using synthetic division,
the remainder is equal to p(c).
Proof of the Remainder Theorem
From our previous work, any number cused in synthetic division will occur as the factor
( ) when written as .
Here, q(x) represents the quotient polynomial and r is a constant. Evaluating p(c) gives
✓
The Factor Theorem
Given a polynomial p(x),
(1) if p(c) 0, then is a factor of p(x), and
(2) if is a factor of p(x), then p(c) 0.
Proof of the Factor Theorem
1. Consider a polynomial p written in the form . From the
remainder theorem we know , and substituting p(c) for r in the equation
shown gives:
and is a factor of p(x), if
✓
2. The steps from part 1 can be reversed, since any factor ( ) of p(x), can be written
in the form . Evaluating at produces a result of zero:
✓
Complex Conjugates Corollary
Given p(x) is a polynomial with real number coefficients, complex solutions must occur
in conjugate pairs. If is a solution, then must also be a solution.
To prove this for polynomials of degree , we let
be complex numbers, and let represent their conjugates,
and observe the following properties:
1. The conjugate of a sum is equal to the sum of the conjugates.
✓
1a c2 1b d2i
→ conjugate of sum → 1a c2 1b d2i
1a bi2 1c di21a bi2 1c di2
sum of conjugates: z
1
z
2
sum: z
1
z
2
z
1
a bi, and z
2
c di
z
1
a bi and z
2
c din 7 2
a bia bi, b 0
0
p1c2 1c c2q1x2
x cp1x2 1x c2q1x2
x c
p1x2 1x c2q1x2
p1c2 0x c
p1x2 1x c2q1x2 p1c2
p1c2 r
p1x2 1x c2q1x2 r
x c
x c
r
0
#
q1c2 r
p1c2 1c c2q1c2 r
p1x2 1x c2q1x2 r
1quotient21divisor2 remainder: p1x2 1x c2q1x2 rx c
x c
Selected Proofs
APPENDIX IV
A-7
College Algebra and Trigonometry—
cob19529_app_A1-A14.qxd 01/02/2009 08:03 PM Page A-7 ssen 1 HD 506:broker:MHDQ092-APP:
A-8 Appendix IV Selected Proofs
2. The conjugate of a product is equal to the product of the conjugates.
✓
Since polynomials involve only sums and products, and the complex conjugate of
any real number is the number itself, we have the following:
Proof of the Complex Conjugates Corollary
Given polynomial
,
where
are real numbers and is a zero of p, we must show that is
also a zero.
evaluate p (x) at z
given
conjugate both sides
property 1
property 2
conjugate of a real number is the number
✓ result
An immediate and useful result of this theorem is that any polynomial of odd
degree must have at least one real root.
Linear Factorization Theorem
If p(x) is a complex polynomial of degree , then p has exactly n linear factors
and can be written in the form p(x) a
n
(x c
1
)(x c
2
) . . . (x c
n
), where
and c
1
, c
2
, . . . , c
n
are complex numbers. Some factors may have multiplicities greater
than 1 (c
1
, c
2
, . . . , c
n
are not necessarily distinct).
Proof of the Linear Factorization Theorem
Given p(x) a
n
x
n
a
n1
x
n1
. . .
a
1
x a
0
is a complex polynomial, the Funda-
mental Theorem of Algebra establishes that p(x) has a least one complex zero, call
it c
1
. The factor theorem stipulates (x c
1
) must be a factor of P, giving
where q
1
(x) is a complex polynomial of degree .
Since q
1
(x) is a complex polynomial in its own right, it too must also have a
complex zero, call it c
2
. Then ( ) must be a factor of q
1
(x), giving
where q
2
(x) is a complex polynomial of degree .
Repeating this rationale n times will cause p(x) to be rewritten in the form
where q
n
(x) has a degree of , a nonzero constant typically called a
n
.
The result is , and the proof is
complete.
p1x2 a
n
1x c
1
21x c
2
2
#
. . .
#
1x c
n
2
n n 0
p1x2 1x c
1
21x c
2
2
#
. . .
#
1x c
n
2q
n
1x2
n 2
p1x2 1x c
1
21x c
2
2q
2
1x2
x c
2
n 1
p1x2 1x c
1
2q
1
1x2
a
n
0
##
n 1
p1z
2 0
a
n
1z
n
2 a
n1
1z
n1
2
p
a
1
1z
1
2 a
0
0
a
n
1z
n
2 a
n1
1z
n1
2
p
a
1
1z
1
2 a
0
0
a
n
z
n
a
n1
z
n1
p
a
1
z
1
a
0
0
a
n
z
n
a
n1
z
n1
p
a
1
z
1
a
0
0
p 1z2 0 a
n
z
n
a
n1
z
n1
p
a
1
z
1
a
0
0
a
n
z
n
a
n1
z
n1
p
a
1
z
1
a
0
p1z2
z
a biz a bia
1
, a
0
a
n
, a
n1
,
p
,
p1x2 a
n
x
n
a
n1
x
n1
p
a
1
x
1
a
0
1ac bd2 1ad bc2i→ conjugate of product → 1ac bd2 1ad bc2i
ac adi bci bdi
2
ac adi bci bdi
2
1a bi2
#
1c di21a bi2
#
1c di2
product of conjugates: z
1
#
z
2
product: z
1
#
z
2
College Algebra and Trigonometry—
cob19529_app_A1-A14.qxd 01/15/2009 04:01 PM Page A-8

Appendix IV Selected Proofs A-9
Proofs from Chapter 4
The Product Property of Logarithms
Given M, N, and are positive real numbers,
log
b
(MN) .
Proof of the Product Property
For and , we have and in exponential form.
It follows that
substitute b
P
for M and b
Q
for N
properties of exponents
log property 3
substitute log
b
M for P and log
b
N for Q
The Quotient Property of Logarithms
Given M, N, and
b 1
are positive real numbers,
.
Proof of the Quotient Property
For and , we have and in exponential form.
It follows that
substitute b
P
for M and b
Q
for N
properties of exponents
log property 3
substitute log
b
M for P and log
b
N for Q
The Power Property of Logarithms
Given M and are positive real numbers and any real number x,
.
Proof of the Power Property
For , we have in exponential form.
It follows that
substitute b
P
for M
properties of exponents
log property 3
substitute log
b
M for P
rewrite factors x log
b
M
1log
b
M2x
Px
log
b
1b
Px
2
log
b
1M2
x
log
b
1b
P
2
x
b
P
MP log
b
M
log
b
M
x
x log
b
M
b 1
log
b
M log
b
N
P Q
log
b
1b
PQ
2
log
b
a
M
N
b log
b
a
b
P
b
Q
b
b
Q
Nb
P
MQ log
b
NP log
b
M
log
b
a
M
N
b log
b
M log
b
N
log
b
M log
b
N
P Q
log
b
1b
PQ
2
log
b
1MN2 log
b
1b
P
b
Q
2
b
Q
Nb
P
MQ log
b
NP log
b
M
log
b
M log
b
N
b 1
College Algebra and Trigonometry—
cob19529_app_A1-A14.qxd 01/15/2009 04:01 PM Page A-9
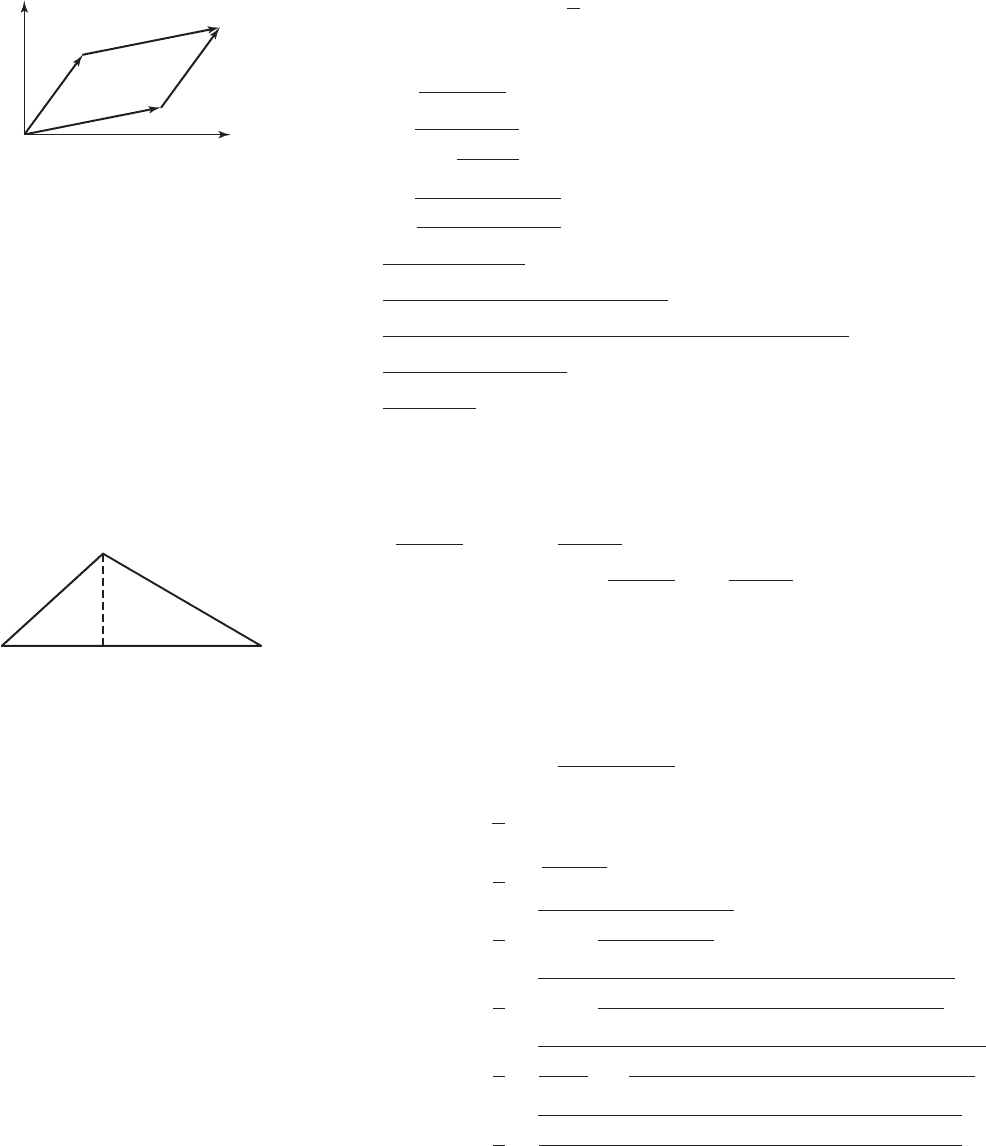
A-10 Appendix IV Selected Proofs
Proof of the Determinant Formula for the
Area of a Parallelogram
Since the area of a triangle is the area of the corresponding parallelogram
is twice as large: In terms of the vectors and we
have and it follows that
Pythagorean identity
substitute for
common denominator
simplify
substitute
expand
simplify
factor
result
Proof of Heron’s Formula Using Algebra
Note that It follows that
This shows:
1
2
b
B
4b
2
c
2
b
4
2b
2
c
2
2a
2
b
2
2a
2
c
2
a
4
c
4
4b
2
1
2
b
B
4b
2
c
2
4b
2
a
b
4
2b
2
c
2
2a
2
b
2
2a
2
c
2
a
4
c
4
4b
2
b
1
2
b
B
c
2
a
b
4
2b
2
c
2
2a
2
b
2
2a
2
c
2
a
4
c
4
4b
2
b
1
2
b
B
c
2
a
b
2
c
2
a
2
2b
b
2
1
2
b2c
2
e
2
A
1
2
bh
b
2
c
2
a
2
2b
e
a
2
b
2
c
2
2be
a
2
b
2
2be e
2
c
2
e
2
a
2
1b e2
2
c
2
e
2
a
2
d
2
c
2
e
2
2a
2
d
2
2c
2
e
2
2a
2
d
2
h 2c
2
e
2
.
ad bc
21ad bc2
2
2a
2
d
2
2acbd b
2
c
2
2a
2
c
2
a
2
d
2
b
2
c
2
b
2
d
2
1a
2
c
2
2acbd b
2
d
2
2
21a
2
b
2
21c
2
d
2
2 1ac bd2
2
2
u
2
v
2
1u
#
v2
2
u
v
B
u
2
v
2
1u
#
v2
2
u
2
v
2
cos
u
v
B
1
1u
#
v2
2
u
2
v
2
Area
u
v
21 cos
2
,
A
u
v
sin ,
v Hc, dI,u Ha, bIA ab sin .
A
1
2
ab sin ,
u
v
a h c
d e
b
cob19529_app_A1-A14.qxd 01/15/2009 04:01 PM Page A-10

Appendix IV Selected Proofs A-11
From this point, the conclusion of the proof is the same as the trigonometric develop-
ment found on page 730.
Proof that u v comp
v
u |v|
Consider the vectors in the figure shown, which form a triangle. Applying the Law of
Cosines to this triangle yields:
Using properties of the dot product (page 758), we can rewrite the left-hand side as
follows:
Substituting the last expression for from the Law of Cosines gives
.
Substituting comp
v
u for completes the proof:
Proof of DeMoivre’s Theorem:
For we proceed using mathematical induction.
1. Show the statement is true for (base case):
2. Assume the statement is true for (induction hypothesis):
3. Show the statement is true for
cos31k 12x4 i sin31k 12x4
✓
cos1kx2cos x sin1kx2sin x i3cos1kx2sin x sin1kx2cos x4
3cos1kx2 i sin1kx241cos x i sin x2
1cos x i sin x2
k1
1cos x i sin x2
k
1cos x i sin x2
1
n k 1:
1cos x i sin x2
k
cos1kx2 i sin1kx2
n k
cos x i sin x cos x i sin x
✓
1cos x i sin x2
1
cos11x2 i sin11x2
n 1
n 7 0,
(cos x i sin x)
n
cos(nx) i sin(nx)
0v0u
#
v comp
v
u
0u0 cos
0v0 0u0cos
u
#
v 0u00v0cos
2 u
#
v 2 0u00v0 cos
0u0
2
2 u
#
v 0v0
2
0u0
2
0v0
2
2 0u00v0 cos
0u v0
2
0u0
2
2 u
#
v 0v0
2
u
#
u u
#
v v
#
u v
#
v
0u v0
2
1u v2
#
1u v2
0u v0
2
0u0
2
0v0
2
20u00v0 cos
1
4
21a b c21a b c21c a b21c a b2
1
4
231a b2
2
c
2
43c
2
1a b2
2
4
1
4
22a
2
b
2
2a
2
c
2
2b
2
c
2
a
4
b
4
c
4
induction hypothesis
F-O-I-L
sum/difference identities
u
v
u – v
x
z
y
cob19529_app_A1-A14.qxd 01/15/2009 05:24 PM Page A-11

A-12 Appendix IV Selected Proofs
By the principle of mathematical induction, the statement is true for all positive
integers. For (the theorem is obviously true for ), consider a positive
integer m, where
negative exponent property
DeMoivre’s theorem for
even/odd identities
n m
cos1nx2 i sin1nx2
cos1mx2 i sin1mx2
cos1mx2 i sin1mx2
n 7 0
1
cos1mx2 i sin1mx2
1
1cos x i sin x2
m
1cos x i sin x2
n
1cos x i sin x2
m
n m.
n 0n 6 0
multiply numerator and denom by
and simplifycos1mx2 i sin1mx2
cob19529_app_A1-A14.qxd 01/15/2009 05:25 PM Page A-12
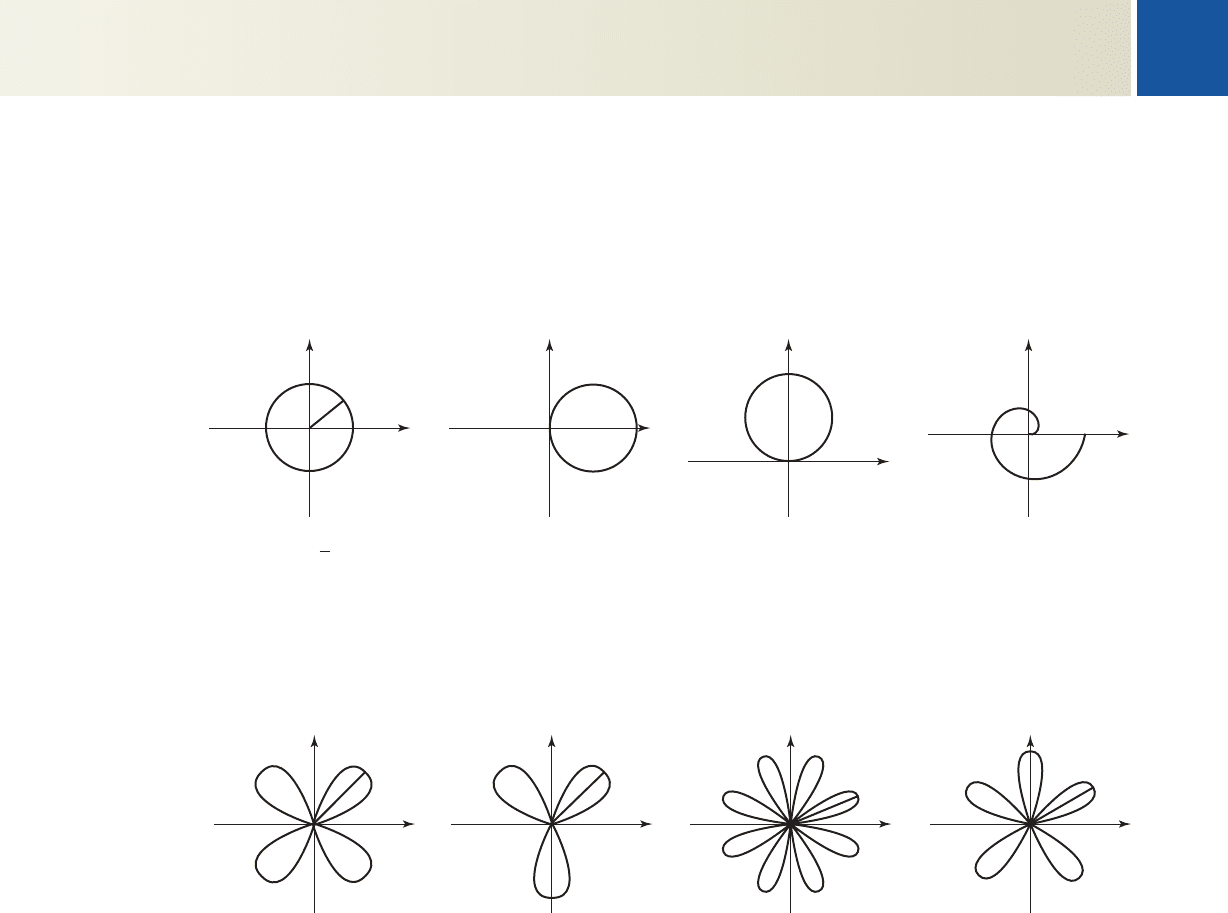
A-13
Families of Polar Curves
APPENDIX V
Circle
r
Circle
r a cos
a represents the diameter of the circle
Circle
r a sin
Spiral
r k
r
a
a
a
2
Four-petal rose
r a sin(2)
Three-petal rose
r a sin(3)
If n is odd S there are n petals, if n is even S there are 2n petals.
|a| represents the maximum distance from the origin
(the radius of a circumscribed circle)
Eight-petal rose
r a sin(4)
Five-petal rose
r a sin(5)
aa
a
a
Circles and Spiral Curves
Roses: (illustrated here) and
r a cos(n)r a sin(n)
College Algebra and Trigonometry—
cob19529_app_A1-A14.qxd 01/02/2009 08:03 PM Page A-13 ssen 1 HD 506:broker:MHDQ092-APP:
