Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.


1010 CHAPTER 10 Analytic Geometry and the Conic Sections 10-92
College Algebra & Trignometry—
For the conic equations given, determine if the equation represents a parabola, ellipse, or hyperbola. Then describe and
sketch the graphs using polar graph paper.
31. 32. 33.
34. Mars has a perihelion of 128.4 million miles and an aphelion of 154.9 million miles. Use this information to find
a polar equation that models the elliptical orbit, then find the length of the focal chord.
SECTION 10.7 Parametric Equations and Graphs
KEY CONCEPTS
• If we consider the set of points P(x, y) such that the x-values are generated by f(t) and the y-values are generated
by g(t) (assuming f and g are both defined on an interval of the domain), the equations and are
called parametric equations, with parameter t.
• Parametric equations can be converted to rectangular form by eliminating the parameter. This can sometimes be
done by solving for t in one equation and substituting in the other, or by using trigonometric forms.
• A function can be written in parametric form many different ways, by altering the parameter or using
trigonometric identities.
• The cycloids are an important family of curves, with equations and
• The solutions to dependent systems of equations are often expression in parametric form, with the points P(x, y)
given by the parametric equations generating solutions to the system.
EXERCISES
Graph the curves defined by the parametric equations over the specified interval and identify the graph. Then eliminate
the parameter and write the corresponding rectangular form.
35. 36. 37.
38. Write the function in three different forms by altering the parameter:
39. Use a graphing calculator to graph the Lissajous figure indicated, then state the size of the rectangle needed to
frame it: x 4 sin15t2; y 8 cos t
y 21x 52
2
1
y 4 cos ty 1t 32
2
y 2t
2
3
x 3 sin t: t 30, 22:x 12 t2
2
: t 30, 54:x t 4: t 33, 34:
y r11 cos t2.x r1t sin t2
y g1t2x f1t2
r
4
3 3 sin
r
8
4 6 cos
r
9
3 2 cos
MIXED REVIEW
For Exercises 1 through 16, graph the conic section and
locate the center, vertices, directrix, foci, focal chords,
asymptotes, and other important features as these apply
to a particular equation and conic.
1.
2.
3.
4.
5.
6.
7.
8.
9. x y
2
2y 3
x y
2
8y 11
y 2x
2
10x 15
161x 22
2
41y 12
2
64
41x 12
2
361y 22
2
144
1x 32
2
9
1y 12
2
25
1
9y
2
25x
2
225
16x
2
25y
2
400
9x
2
9y
2
54
10.
11.
12.
13.
14.
15.
16.
17. Graph the curve defined by the parametric equations
given, using the interval . Then identify
the graph:
18. Plot the polar coordinates given, then convert to
rectangular coordinates.
a. b. a4,
5
4
ba3.5,
2
3
b
x 1t 22
2
, y 1t 42
2
t 30, 104
x
2
y
2
8x 12y 16 0
491x 22
2
1y 32
2
49
4x
2
16y
2
12x 48y 19 0
4x
2
25y
2
24x 150y 289 0
x
2
24y
x
2
8x 8y 16 0
x 1y 22
2
3
cob19529_ch10_1007-1016.qxd 12/6/08 4:44 AM Page 1010 epg HD 049 :Desktop Folder:Satya 05/12/08:
10-93 Practice Test 1011
College Algebra & Trignometry—
19. Solve using elimination:
a. b.
20. Match each equation to its corresponding graph.
Justify each response.
(i)
(ii)
(iii)
a.
b.
c.
(4.5, 0)
(4.5, 0)
4.5
r 4.5 cos
r
2
20.25 sin122
r 3.5 cos
e
4x
2
9y
2
36
x
2
3y 6
e
4x
2
y
2
9
x
2
3y
2
79
21. A go-cart travels around an elliptical track with a
100-m major axis that is horizontal. The minor axis
measures 60 m. Write an equation model for the
track in parametric form.
22. Except for small variations, a planet’s orbit around
the Sun is elliptical, with the Sun at one focus. The
perihelion or minimum distance from the planet
Mercury to the Sun is about 46 million kilometers.
Its aphelion or maximum distance from the Sun is
approximately 70 million kilometers. Use this
information to find the length of the major and
minor axes, then determine the equation model
for the orbit of Mercury in the standard form
23. The orbit of a comet can also be modeled by one of
the conic sections, with the Sun at one focus.
Assuming the equations given model a comet’s path,
(1) determine if the path is circular, elliptic,
hyperbolic, or parabolic; and (2) determine the
closest distance the comet will come to the Sun (in
millions of miles).
a. b.
24. In the design of their corporate headquarters,
Centurion Computing includes a seven-leaf rose in a
large foyer, with a fountain in the center. Each of the
leaves is 5 m long (when measured from the center
of the fountain), and will hold flower beds for
carefully chosen perennials. The rose is to be
symmetric to a vertical axis, with the leaf bisected
by pointing directly to the elevators. Find the
equation of the rose in polar form.
25. The hyperbola defined by in the
XY-plane is rotated clockwise by What is the
corresponding equation in the xy-plane?
45°.
X
2
80
2
Y
2
400
2
1
2
r
31
5 5 sin
r
84
100 70 cos
x
2
a
2
y
2
b
2
1.
PRACTICE TEST
By inspection only (no graphing), match each equation
to its correct description.
1.
2.
3.
4.
a. Parabola b. Hyperbola c. Circle d. Ellipse
y x
2
4x 20 0
x
2
4y
2
4x 12y 20 0
4y
2
x
2
4x 8y 20 0
x
2
y
2
6x 4y 9 0
Identify and then graph each of the following conic
sections. State the center, vertices, foci, asymptotes, and
other important points when applicable.
5.
6.
7. 8. r
12
5 5 cos
r
10
5 4 cos
251x 22
2
41y 12
2
100
x
2
y
2
4x 10y 20 0
cob19529_ch10_1007-1016.qxd 12/6/08 12:52 AM Page 1011 epg HD 049 :Desktop Folder:Satya 05/12/08:
1012 CHAPTER 10 Analytic Geometry and the Conic Sections 10-94
College Algebra & Trignometry—
9.
10.
Use the equation
to complete Exercises 11 and 12.
11. Use the discriminant to identify the
graph, and to find and
12. Find the equation in the xy-plane and use a rotation of
axes to draw a neat sketch of the graph in the XY-plane.
Graph each polar equation.
13. 14.
15.
For Exercises 16 and 17, identify and graph each conic
section from the parametric equations given. Then
remove the parameter and convert to rectangular form.
16. 17.
18. Use a graphing calculator to graph the cycloid, then
identify the maximum and minimum values, and the
period.
19. Solve each nonlinear system using the technique of
your choice.
a. b.
20. Halley’s comet has a perihelion of 54.5 million
miles and an aphelion of 3253 million miles. Use
this information to find a polar equation that models
its elliptical orbit. How does its eccentricity compare
with that of the planets in our solar system?
21. The soccer match is tied, with time running out. In a
desperate attempt to win, the opposing coach pulls
his goalie and substitutes a forward. Suddenly,
Marques gets a break-away and has an open shot at
the empty net, 165 ft away. If the kick is on-line and
leaves his foot at an angle of with an initial
velocity of 80 ft/sec, is the ball likely to go in the net
and score the winning goal?
28°
e
4y
2
x
2
4
x
2
y
2
4
e
4x
2
y
2
16
y x 2
x 4T 4 sin T y 4 4 cos T
y t 2y 5 cos t
x 1t 32
2
1x 4 sin t
r 6 sin122
r 4 8 cos r 3 3 cos
sin .cos tan122
B
A C
B
2
4AC
44 0
80x
2
120xy 45y
2
100y
41x 12
2
251y 22
2
100
1y 32
2
9
1x 22
2
16
1
22. The orbit of Mars around the Sun is elliptical, with
the Sun at one foci. When the orbit is expressed as a
central ellipse on the coordinate grid, its equation is
. Use this information to
find the aphelion of Mars and the perihelion of Mars
in millions of miles.
Determine the equation of each relation and state its
domain and range. For the parabola and the ellipse, also
give the location of the foci.
23.
24.
25.
(5, 1)
(2, 6)
(1, 1)
(2, 4)
x
y
(4, 1)
(3, 4)
(6, 1)
(5, 2)
x
y
(1, 0)
(1, 4)
(3, 0)
(0, 3)
x
y
x
2
1141.652
2
y
2
1141.032
2
1
CALCULATOR EXPLORATION AND DISCOVERY
While all planets orbit
around the sun in an
elliptical path, their
ecliptic planes, or the
planes containing the orbits, differ considerably. For
example, using the ecliptic plane of the Earth for refer-
ence, the plane containing Mercury’s orbit is inclined by
and the plane of the dwarf planet Pluto by ! In addi-
tion, if we use the major axis of Earth’s orbit for reference,
the major axes of the other planets, assuming they are
transformed to the ecliptic plane, are rotated by some
angle We can gain a basic understanding of the rotations.
17°7°
Conic Rotations in Polar Form
Sun
cob19529_ch10_1007-1016.qxd 12/6/08 4:44 AM Page 1012 epg HD 049 :Desktop Folder:Satya 05/12/08:
10-95 Strengthening Core Skills 1013
College Algebra & Trignometry—
of an elliptical path (relative to some point of reference)
using skills developed in this chapter. Here we’ve seen that
the equation of a conic can be given in rectangular form,
polar form, and parametric form. Each form seems to have
its advantages. When it comes to the rotations of a conic
section, it’s hard to match the ease and versatility of the
polar form. To illustrate, recall that in polar form the
general equation of a horizontal ellipse with one focus (the
Sun) at the origin is The constant a gives
the length of the semimajor axis and e represents the
eccentricity of the orbit. With the exception of Mercury
and Pluto (a dwarf planet), the orbits of most planets are
close to circular (e is very near zero). This makes the rota-
tions difficult to see. Instead we will explore the concept
of axes rotation using “planets” with higher eccentricities.
Consider the following planets and their orbital equations.
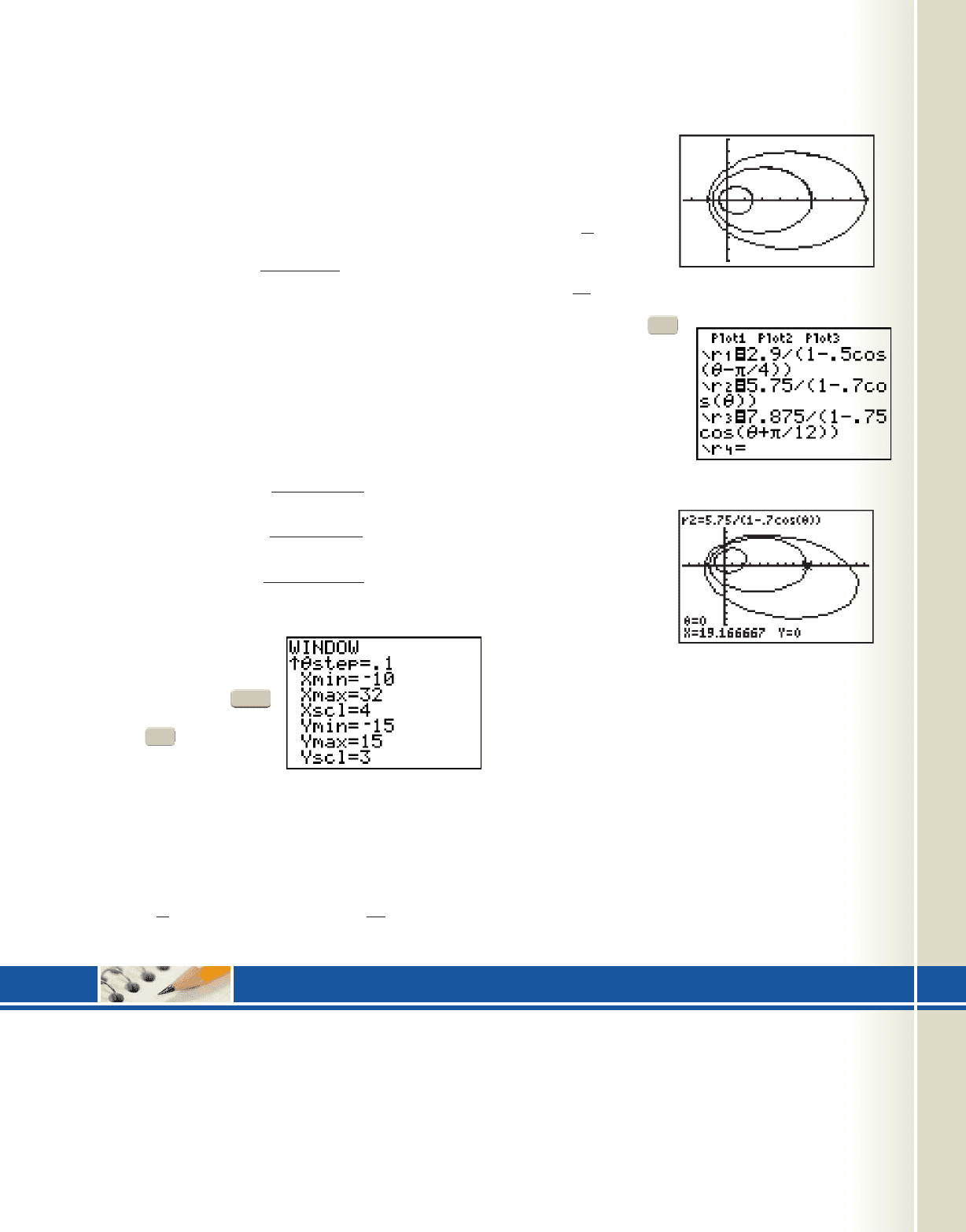
The planet Agnesi has an eccentricity of while the
planet Erdös is the most eccentric at
We’ll investigate the
concept of conic rotations
in polar form by rotating
these ellipses. With your
calculator in polar ,
enter these three equations
on the screen and use
the settings shown in Figure
10.77 to set the window
size (use ).
The resulting graph is displayed in Figure 10.78,
showing the very hypothetical case where all planets share
the same major axis. To show a more realistic case where
the planets approach the Sun along orbits with differing
major axes, we’ll use Galois as a reference and rotate
Agnesi rad clockwise and Erdös rad counter-
12
4
max 7
Y =
MODE
Erdös:
7.875
1 0.75 cos
Galois:
5.75
1 0.7 cos
Agnesi:
2.9
1 0.5 cos
e 0.75.
e 0.5,
r
a11 e
2
2
1 e cos
.
clockwise.
This is done by
simply adjusting
the argument of
cosine in each
equation, using
for
Agnesi and
for
Erdös. The adjusted
screen is shown in Figure
10.79, and new graphs in
Figure 10.80.
Use these ideas to
explore and investigate
other rotations by com-
pleting the following
exercises.
Exercise 1: What
happens if the
angle of rotation is
? Is the orbit
identical if you
rotate by ?
Exercise 2: If the
denominator in
the equation is
changed to a sum, what effect does it have on the graph?
Exercise 3: If the sign in the numerator is changed, what
effect does it have on how the graph is generated?
Exercise 4: After resetting the orbits as originally given,
use trial and error to approximate the smallest angle of
rotation required for the orbit of Galois to intersect the
orbit of Erdös.
Exercise 5: What minimum rotation is required for the
orbit of Galois to intersect the orbit of both Agnesi and
Erdös?
Exercise 6: What is the minimum rotation required for
the orbit of Agnesi to intersect the orbit of Galois?
Y =
cosa
12
b
cosa
4
b
15
10
15
32
Figure 10.77
Figure 10.78
Figure 10.80
15
10
15
32
STRENGTHENING CORE SKILLS
Simplifying and
Streamlining
Computations for the
Rotation of Axes
While the calculations involved for eliminating the mixed xy-term require a good deal
of concentration, there are a few things we can do to simplify the overall process. Basi-
cally this involves two things. First, in Figure 10.81 we’ve organized the process in
flowchart form to help you “see” the sequence involved in finding and (for
use in the rotation formulas). Second, calculating x
2
, y
2
, and xy (from the equations
and ) as single terms and apart from
their actual substitution is somewhat less restrictive and seems to help to streamline
the algebra.
y X sin Y cos x X cos Y sin
sin cos
Figure 10.79
cob19529_ch10_1007-1016.qxd 12/6/08 12:52 AM Page 1013 epg HD 049 :Desktop Folder:Satya 05/12/08:

1014 CHAPTER 10 Analytic Geometry and the Conic Sections 10-96
Illustration 1
For use a rotation of axes to eliminate
the xy-term, then identify the conic and its characteristic features.
Solution
Since we find using , giving
Using the triangle shown in Figure 10.82 we find
We then find the values of and (choosing
in QII), using the double-angle identities as follows:
We now compute x
2
, xy, and y
2
prior to substitution in the original equation, writing
each as a single term:
2
113
Q
1
5
13
2
S
Q
8
13
2
sin
A
1 cos122
2
3
113
Q
1
5
13
2
S
Q
18
13
2
cos
A
1 cos122
2
2
sin cos cos122
5
13
.
tan122
12
5
.
tan122
B
A C
A C,
2x
2
12xy 3y
2
42 0,
12
5
13
2
Figure 10.82
College Algebra & Trignometry—
Is A C?
(B 0)
Find sin(2) and cos(2) from the
triangle corresponding to tan(2),
then cos and sin from
the double-angle identities.
 45
 30
or
 60
B
A C
Is
no
yes
1
兹
3
or
兹
3?
Use cos  and sin  in the rotation
formulas to compute x
2
, xy, and y
2
,
writing each as a single term.
Substitute, simplify, and
use the invariants to
double-check your work.
no
yes
Figure 10.81
•
•
9X
2
12XY 4Y
2
13
x
2
a
3X 2Y
113
b
2
x
3
113
X
2
113
Y
3X 2Y
113
•
•
4X
2
12XY 9Y
2
13
y
2
a
2X 3Y
113
b
2
y
2
113
X
3
113
Y
2X 3Y
113
•
6X
2
5XY 6Y
2
13
xy
13X 2Y212X 3Y2
113
Next, we substitute into the original equation, clearing denominators priorto using
the distributive property.
cob19529_ch10_1007-1016.qxd 01/14/2009 05:08 PM Page 1014 ssen 1 HD 049:Desktop Folder:Satya 14/01/09:Used file:MHDQ092-10:
10-97 Cumulative Review Chapters 1–10 1015
College Algebra & Trignometry—
Solve each equation.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10. Use De Moivre’s theorem to find the three cube
roots of . Write the roots in form.
11. The price of beef in Argentina varies directly with
demand and inversely with supply. In the small town
of Chascomus, the tender-cut lomito was selling for
18 pesos/kg last week. There were 1000 kg
available, and 850 kg were bought. Next week there
is a 3-day weekend, so the demand is expected to be
closer to 1400 kg, but the butchers will only be able
to supply 1200 kg. What will a kilogram of tender-
cut lomito cost next week?
12. Find the inverse of .f 1x2 3 sin12x 12
a bi8i
sin 27°
18
sin x
35
25 sina
3
x
6
b 3 15.5
6 tan x 213
log
3
x log
3
1x 22 1
log
3
81 x
3
x2
7
4
#
2
x1
1
8
x
2
6x 13 0
1x 2
2 13x 4
13. A surveyor needs to estimate the width of a large
rock formation in Canyonlands National Park. From
her current position she is 540 yd from one edge of
the formation and 850 yd from the other edge. If the
included angle is , how wide is the formation?
Graph each relation. Include vertices, x- and y-intercepts,
asymptotes, and other features.
14.
15.
16.
17.
18.
19.
20.
21.
22. y 2 cosax
4
b 1
41x 12
2
361y 22
2
144
x
2
y
2
10x 4y 20 0
f1x2 log
2
1x 12
y 2
x
3
h1x2
x 2
x
2
9
g1x2 1x 321x 121x 42
y 1x 3
1
f1x2
x 2
3
850 yd
110
540 yd
110°
CUMULATIVE REVIEW CHAPTERS 1–10
combine like terms
simplify and check invariants:
✓
standard form
✓
The graph is a central hyperbola along the X-axis, with vertices at
and asymptotes
Exercise 1: Return to Section 10.6 and resolve Exercises 31 and 32 using these
methods. Do the new ideas make a difference?
Y
A
6
7
X.
117
, 02
B
2
4AC b
2
4ac
1
X
2
1172
2
Y
2
1162
2
F f ✓
A C a c 42 6X
2
7Y
2
546 78X
2
91Y
2
60XY 72Y
2
12X
2
36XY 27Y
2
546 18X
2
24XY 8Y
2
72X
2
12a
6X
2
5XY 6Y
2
13
b 3a
4x
2
12XY 9Y
2
13
b42 2a
9X
2
12XY 4Y
2
13
b
42 2x
2
12xy 3y
2
multiply both sides by 13, then distribute
cob19529_ch10_1007-1016.qxd 12/6/08 5:18 AM Page 1015 epg HD 049 :Desktop Folder:Satya 05/12/08:

College Algebra & Trignometry—
23.
24.
25. Use the dot product to find the angle between the
vectors and
Solve each system of equations.
26.
27.
28. Find the equation of the parabola with vertex at
(2, 3) and directrix .x 0
e
x
2
y
2
25
64x
2
12y
2
768
•
4x 3y 13
9y 5z 19
x 4z 4
v H3, 7I.u H4, 5I
y tan t
x 2 sin t
r 4 cos122
29. Decompose into partial
fractions.
30. In the summer, Hollywood releases its big
budget, big star, big money movies. Suppose
the weekly summer revenue generated by
ticket sales was modeled by the function
,
where R(w) represents the revenue generated in
week w and . Use the remainder
theorem to determine the amount of revenue
generated in week 5.
1 w 12
R1w2w
4
25w
3
200w
2
560w 234
y
3x
3
2x
2
x 3
x
4
x
2
1016 CHAPTER 10 Analytic Geometry and the Conic Sections 10-98
cob19529_ch10_1007-1016.qxd 12/6/08 12:52 AM Page 1016 epg HD 049 :Desktop Folder:Satya 05/12/08:

Additional Topics
in Algebra
CHAPTER OUTLINE
11.1 Sequences and Series 1018
11.2 Arithmetic Sequences 1027
11.3 Geometric Sequences 1034
11.4 Mathematical Induction 1044
11.5 Counting Techniques 1053
11.6 Introduction to Probability 1065
11.7 The Binomial Theorem 1077
11
11
CHAPTER CONNECTIONS
For a corporation of any size, decisions made
by upper management often depend on a
large number of factors, with the desired
outcome attainable in many different ways.
For instance, consider a legal firm that
specializes in family law, with a support staff
of 15 employees—6 paralegals and 9 legal
assistants. Due to recent changes in the law,
the firm wants to send some combination of
five support staff to a conference dedicated
to the new changes. In Chapter 11, we’ll see
how counting techniques and probability can
be used to determine the various ways such a
group can be randomly formed, even if certain
constraints are imposed. This application
appears as Exercise 34 in Section 11.6.
Check out these other real-world connections:
Determining the Effects of Inflation
(Section 11.1, Exercise 86)
Counting the Number of Possible Area Codes
and Phone Numbers (Section 11.5, Exercise 84)
Calculating Possible Movements of a Computer
Animation (Section 11.2, Exercise 73)
Tracking and Improving Customer Service
Using Probability (Section 11.6, Exercise 53)
1017
College Algebra & Trignometry—
cob19529_ch11_1017-1096.qxd 12/8/08 21:29 Page 1017
A sequence can be thought of as a pattern of numbers listed in a prescribed order. A
series is the sum of the numbers in a sequence. Sequences and series come in count-
less varieties, and we’ll introduce some general forms here. In following sections we’ll
focus on two special types: arithmetic and geometric sequences. These are used in a
number of different fields, with a wide variety of significant applications.
A. Finding the Terms of a Sequence Given the General Term
Suppose a person had $10,000 to invest, and decided to place the money in govern-
ment bonds that guarantee an annual return of 7%. From our work in Chapter 4, we
know the amount of money in the account after x years can be modeled by the func-
tion If you reinvest your earnings each year, the amount in the
account would be (rounded to the nearest dollar):
Year: f(1) f(2) f(3) f(4) f(5)...
Value: $10,700 $11,449 $12,250 $13,108 $14,026...
Note the relationship (year, value) is a function that pairs 1 with $10,700, 2 with
$11,449, 3 with $12,250 and so on. This is an example of a sequence. To distinguish
sequences from other algebraic functions, we commonly name the functions a instead
of f, use the variable n instead of x, and employ a subscript notation. The function
would then be written Using this notation
and so on.
The values are called the terms of the sequence. If the account
were closed after a certain number of years (for example, after the fifth year) we have
a finite sequence. If we let the investment grow indefinitely, the result is called an infi-
nite sequence. The expression a
n
that defines the sequence is called the generalor nth
term and the terms immediately preceding it are called the term, the
term, and so on.
Sequences
A finite sequence is a function a
n
whose domain is the set of natural numbers from
1 to n. The terms of the sequence are labeled
where a
k
represents an arbitrary “interior” term and also represents the last term
of the sequence.
An infinite sequence is a function whose domain is the set of all
natural numbers.
EXAMPLE 1A
Computing Specified Terms of a Sequence
For find a
1
, a
3
, a
6
, and a
7
.
Solution
EXAMPLE 1B
Computing the First k Terms of a Sequence
Find the first four terms of the sequence Write the terms of the
sequence as a list.
a
n
112
n
2
n
.
a
6
6 1
6
2
7
36
a
7
7 1
7
2
8
49
a
1
1 1
1
2
2
a
3
3 1
3
2
4
9
a
n
n 1
n
2
,
a
n
a
n
a
1
, a
2
, a
3
, p , a
k
, a
k1
, p , a
n1
, a
n
1n 22nd
1n 12st
a
1
, a
2
, a
3
, a
4
, p
a
1
10,700, a
2
11,449,
a
n
10,00011.072
n
.f 1x2 10,00011.072
x
TTTTT
f 1x2 10,00011.072
x
.
Learning Objectives
In Section 11.1 you will learn how to:
A. Write out the terms of a
sequence given the
general or nth term
B. Work with recursive
sequences and
sequences involving a
factorial
C. Find the partial sum of a
series
D. Use summation notation
to write and evaluate
series
E. Use sequences to solve
applied problems
11.1 Sequences and Series
WORTHY OF NOTE
Sequences can actually start
with any natural number. For
instance, the sequence
must start at
to avoid division by
zero. In addition, we will
sometimes use a
0
to indicate
a preliminary or inaugural
element, as in
for the amount of money
initially held, prior to
investing it.
a
0
$10,000
n 2
a
n
2
n 1
1018 11-2
College Algebra & Trignometry—
cob19529_ch11_1017-1096.qxd 12/8/08 21:29 Page 1018
11-3 Section 11.1 Sequences and Series 1019
Solution
The sequence can be written 4, 16,..., or more generally as 4,
16, . . . , . . . to show how each term was generated.
Now try Exercises 7 through 32
B. Recursive Sequences and Factorial Notation
Sometimes the formula defining a sequence uses the preceding term or terms to gen-
erate those that follow. These are called recursive sequences and are particularly
useful in writing computer programs. Because of how they are defined, recursive
sequences must give an inaugural term or seed element, to begin the recursion process.
Perhaps the most famous recursive sequence is associated with the work of
Leonardo of Pisa (
A.D. 1180–1250), better known to history as Fibonacci. In fact, it is
commonly called the Fibonacci sequence in which each successive term is the sum of
the previous two, beginning with 1, 1, . . . .
EXAMPLE 2
Computing the Terms of a Recursive Sequence
Write out the first eight terms of the recursive (Fibonacci) sequence defined by
, and
Solution
The first two terms are given, so we begin with
At this point we can simply use the fact that each successive term is simply the
sum of the preceding two, and find that and
The first eight terms are 1, 1, 2, 3, 5, 8, 13, and 21.
Now try Exercises 33 through 38
Sequences can also be defined using a factorial, which is the product of a given
natural number with all those that precede it. The expression 5! is read, “five facto-
rial,” and is evaluated as:
Factorials
For any natural number n,
Rewriting a factorial in equivalent forms often makes it easier to simplify certain
expressions. For example, we can rewrite or Consider
Example 3.
EXAMPLE 3
Simplifying Expressions Using Factorial Notation
Simplify by writing the numerator in an equivalent form.
a. b. c.
6!
3!5!
11!
8!2!
9!
7!
5! 5
#
4
#
3!.5! 5
#
4!
n! n
#
1n 12
#
1n 22
#
p
#
3
#
2
#
1
5! 5
#
4
#
3
#
2
#
1 120.
c
8
13 8 21.
c
6
3 5 8, c
7
5 8 13,
5 3 2
3 2 2 1 1 1
c
4
c
3
c
3
c
2
c
2
c
1
c
5
c
51
c
52
c
4
c
41
c
42
c
3
c
31
c
32
n 3.
c
n
c
n1
c
n2
.c
1
1, c
2
1
112
n
2
n
,
8,2,8,2,
a
3
112
3
2
3
8
a
4
112
4
2
4
16
a
1
112
1
2
1
2
a
2
112
2
2
2
4
WORTHY OF NOTE
When the terms of a
sequence alternate in sign as
in Example 1B, we call it an
alternating sequence.
A. You’ve just learned how
to write out the terms of a
sequence given the general or
nth term
WORTHY OF NOTE
One application of the
Fibonacci sequence involves
the Fibonacci spiral, found
in the growth of many ferns
and the spiral shell of many
mollusks.
College Algebra & Trignometry—
cob19529_ch11_1017-1096.qxd 12/8/08 21:29 Page 1019
