CIMA - C3 Fundamentals Of Business Mathematics
Подождите немного. Документ загружается.


380 Answer bank
76
Year
Cash flow
Discount factor
Present value
$
11%
$
0
(28,000)
1.000
(28,000)
1
8,000
0.901
7,208
2
8,000
0.812
6,496
3
8,000
0.731
5,848
4
8,000
0.659
5,272
5
8,000
0.593
4,744
NPV
1,568
Project viable Yes
9
No
The NPV is positive, therefore the project is viable because it earns more than 11% per annum.
77 (a) A =
$12,000
B =
1
C =
0.641
D =
$15,516
E =
$18,575
F =
$330
Workings
Year
Cash flow
Discount factor
Present value
$
16%
$
0
(50,000)
1.000
(50,000)
1
18,000
0.862
15,516
2
25,000
0.743
18,575
3
15,000
0.641
9,615
4
12,000
0.552
6,624
NPV
330
(b)
–$1,477
Workings
Year
Cash flow
Discount factor
Present value
$
18%
$
0
(50,000)
1.000
(50,000)
18,000
0.847
15,246
2
25,000
0.718
17,950
15,000
0.609
9,135
4
12,000
0.516
6,192
NPV
(1,477)

Answer bank 381
(c)
16.4%
Workings
Estimated IRR = 16% +
()
%1618
477,1330
330
⎥
⎦
⎤
⎢
⎣
⎡
−×
+
= 16.4% (to 1 decimal place).
78 (a) (i)
9.954x
(ii)
$4,018
Workings
The bank pays out the loan now so the present value of the loan is $40,000.
The annuity is the amount that needs to be paid at the end of each quarter.
The annuity factor can be found in the cumulative present value tables; the cost of capital is 3%, and
the number of time periods we are concerned with is found as follows.
Now End of year 1 End of year 2 End of year 3
0 1 2 3 4 1 2 3 4 1 2 3 4
Quarter
Number of time periods = 12 quarters
Annuity factor = 9.954
Present value of repayments = 9.954X
and x =
954.9
000,40$
= $4,018.49
Therefore, the equal amounts that must be repaid at the end of each quarter = $4,018 (to the nearest
$).
(b) (i)
$44,994.56
(ii)
10.787Y
(iii)
$3,290
Workings
(i) In three years' time, the amount of money required to modernise the premises will be:
$40,000
× (1.04)
3
= $44,994.56
(ii) The instalments consist of a payment Y now plus an annuity of 11 payments at 2% per time
period. The annuity factor at 2% for 11 periods is 9.787 and hence the present value is Y +
9.787Y = 10.787Y.
382 Answer bank
(iii) The present value of $44,994.56 at time 12 discounted at 2% = $44,994.56 × 0.788.
∴ 10.787Y = $44,994.56 × 0.788
Y =
787.10
455,35$
= $3,290 (to the nearest $10)
(c) Save and modernise later
9
It costs less to save now and modernise later, therefore the retailer should be advised to do this.
79 B A correlation coefficient close to 1 indicates a strong relationship between two variables.
80 A
II
B
III
C
I
81 D
X
Y
X
2
Y
2
X
Y
1
6
1
36
6
2
5
4
25
10
3
3
9
9
9
4
8
16
64
32
10
22
30
134
57
n = 4
r =
() ()
(
)
(
)
∑−∑∑
∑−∑ ∑−∑
22
22
nXY(X)(Y)
nX X nY Y
=
(
)
(
)
() ( )
22
457 1022
430 10 4134 22
×−×
⎡⎤⎡ ⎤
×− ×× −
⎣⎦⎣ ⎦
=
8
20 52
×
=
8
1040
= 0.248
82 D The formula for the product moment correlation coefficient is provided in your assessment. There
are no excuses for getting this question wrong.
r =
]Y)(Y] [nX)(X[n
YXXYn
2222
∑−∑∑−∑
∑∑−∑
=
]221344[]10304[
)2210()574(
22
−×−×
×−×
=
040,1
8
= +0.25

Answer bank 383
83 D
Critic 1
Critic 2
Rank
Rank
d
d
2
Captain Corelli's guitar
2
1
1
1
Debbie Jones's diary
1
3
2
4
The songs of a bird
4
7
3
9
Cold love in a warm climate
6
5
1
1
Raging wars and peacefulness
5
6
1
1
Charlotte Black
3
2
1
1
The name of the tulip
7
4
3
9
∑d
2
=
26
R = 1 –
⎥
⎦
⎤
⎢
⎣
⎡
−
∑
)1n(n
d6
2
2
= 1 –
⎥
⎦
⎤
⎢
⎣
⎡
−×
×
)149(7
266
= 1 –
336
156
= 0.536
84 C The independent variable is denoted by X and the dependent one by Y. Statement III is therefore
correct. You should have been able to eliminate options B and D straightaway.
The variable to be forecast must always be Y. Statement I is therefore not true.
In calculating the correlation coefficient, it does not matter which variable is X and which is Y, and a
totally different regression line equation will result if X and Y are interchanged. Statement II is
therefore not true.
Scattergraphs are used to show whether or not there is a relationship between X and Y and it does
not matter which variable is associated with a particular axis. Statement IV is therefore not true.
All statements (except for III) are not true. The correct answer is therefore C.
85 D Where y = a + bx
b =
22
X)(Xn
YXXYn
∑−∑
∑∑−∑
=
)21()917(
)18421()5877(
2
−×
×−×
=
196
245
= 1.25
a =
Y
– b
X
=
7
)2125.1(
7
184
×
−
= 22.5
The correct answer is therefore D.

384 Answer bank
86 C The sample of only six pairs of values is very small and is therefore likely to reduce the reliability of
the estimate. Statement I is therefore true.
With such a small sample and the extrapolation required, the estimate is unlikely to be reliable.
Statement II is therefore not true.
Since a correlation coefficient of 0.9 would be regarded as strong (it is a high value) the estimate
would be reliable. Statement III is therefore not true.
When X = 20, we don't know anything about the relationship between X and Y since the sample data
only goes up to X = 10. Statement IV is therefore true.
87 (a) (2, 3)
(3, 4.5)
(4, 6)
?
Perfect positive correlation
Perfect negative correlation
9
Uncorrelated
(b) (2, 3)
(3, 1.5)
(4, 0)
?
Perfect positive correlation
Perfect negative correlation
9
Uncorrelated
(c) (2, 3)
(4, 0)
(4, 6)
?
Perfect positive correlation
Perfect negative correlation
9
Uncorrelated
Workings
(a) If these points were plotted on a scatter diagram, all the pairs of values would lie on an upward-
sloping straight line with a gradient of +1.5.
⎥
⎦
⎤
⎢
⎣
⎡
==
−
−
= 5.1
2
3
24
36
Gradient . This would be indicative
of PERFECT POSITIVE CORRELATION.
(b) If these points were plotted on a scatter diagram, all the pairs of values would lie on a downward-
sloping straight line with a gradient of –1.5.
⎥
⎦
⎤
⎢
⎣
⎡
−=
−
=
−
−
= 5.1
2
3
24
30
Gradient . This would be
indicative of
PERFECT NEGATIVE CORRELATION.
(c) If these points were plotted on a scatter diagram there would not be evidence of any correlation
existing since when x = 4, the corresponding y values are equal to 0 or 6.
88 (a) (i)
1.2830
(ii)
6.68
Workings
The regression line is Y = a + bX
where b =
()
2
2
XXn
YXXYn
∑−∑
∑
∑
−
∑
a =
Y
– b
X
b =
2
8273610
17282492,110
−
×
×
−
×
= 1.2830
a = 17.2 – 1.283 × 8.2 = 6.68
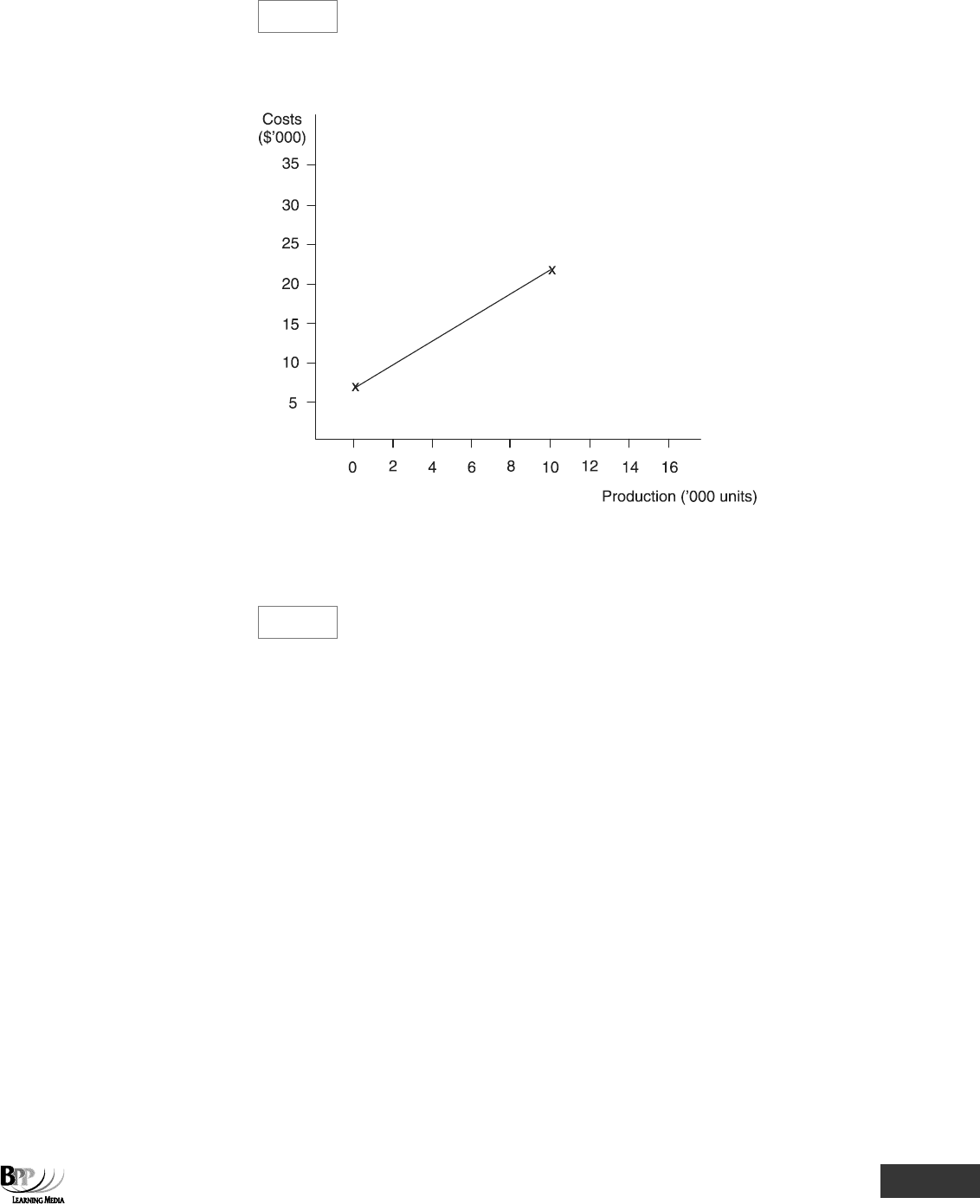
Thus Y = 6.68 + 1.283X ($'000).
Answer bank 385
(b) (i)
7,000
When production is zero, X = 0 and Y = 7.
∴ Fixed costs = $7,000
(ii)
Workings
When X = 0, Y = 7
When X = 10, Y = 7 + 15 = 22
(iii)
$22,000
When production is 10,000, then X = 10 and Y = 22 and total production costs are therefore
$22,000.

386 Answer bank
89 (a)

Answer bank 387
(b)
0.946
Workings
The correlation coefficient, r, is calculated using the following formula.
r =
() ()
]YYn[]XXn[
YXYn
2222
∑
−
∑∑
−
∑
∑∑
−
∑
=
)920,2200,74512)(240110,512(
200,37
22
−×−×
=
000,416720,3
200,37
×
=
531.338,39
200,37
= 0.946
90 A If x = 8, y = 690.24 – (2.75 × 8) = 668.24
Forecast = trend + seasonal component = 668.24 – 25.25 = 642.99 = 643 (to the nearest unit)
If you selected option B, you calculated the forecast for the seventh period and deducted the
seasonal component of the eighth period.
If you selected option C, you correctly forecast the trend for the eighth period but forgot to deduct
the seasonal component.
If you selected option D, you simply calculated the trend for the seventh period instead of the eighth
period.
91 D I Provided the seasonal variation remains the same in the future as in the past, it will not make
forecasts unreliable.
II Provided a multiplicative model is used, the fact that the trend is increasing need not have
any adverse effect on the reliability of forecasts.
III If the model being used is inappropriate, for example, if an additive model is used when the
trend is changing sharply, forecasts will not be very reliable.
IV Forecasts are made on the assumption that everything continues as in the past.
III and IV are therefore necessary and hence the correct answer is D.
92 A I With an additive model, the weekly component represents the average value of actual
production minus the trend for that week, so a component of +9 means production is 9,000
units above the trend.
This is the only correct statement.
If you selected option B, C or D, you have confused the additive variation of –4, +5 and –6
(actually –4,000 units, +5,000 units and –6,000 units respectively) with the multiplicative
variation of –4%, +5% and –6% respectively.

388 Answer bank
93 A
Quarter
1
2
3
4
Total
Unadjusted average
1.09
0.93
1.17
0.78
3.97
Adjustment
0.0075
0.0075
0.0075
0.0075
0.03
Adjusted average
1.0975
0.9375
1.1775
0.7875
4.000
4 – 3.97 = 0.03
We therefore need to add 0.03 ÷ 4 = 0.0075 to each average.
From the table above, it can be seen that the first quarter adjusted average is 1.0975 as per option A.
If you selected option B, you added the entire deficit of 0.03 to the second quarter average instead of
spreading it across all four averages.
If you selected option C, you subtracted the entire deficit of 0.03 from the third quarter average
rather than sharing it across all four averages.
If you selected option D, you have subtracted the deficit of 0.0075 from each quarter's average,
instead of adding it.
94 B As this is a multiplicative model, the seasonal variations should sum (in this case) to 4 (an average
of 1) as there are four quarters.
Let x = seasonal variation for quarter 4.
0.45 + 1.22 + 1.31 + x = 4
2.98 + x = 4
x = 4 – 2.98
= 1.02
If you selected option A you subtracted the sum of the seasonal variations from 3 instead of 4.
If you selected option D, you forgot to subtract the sum of the seasonal variations for quarters 1-3
from 4.
95
Quarter Sales forecast
1 6,591 (W4)
2 7,489 (W3)
3 2,364 (W2)
4 3,358 (W1)
Workings
(1) The trend changes from 4,500 to 5,300. The growth rate is
500,4
300,5
= 1.178 = 17.8%.
Expressed per quarter (there are four quarters) this is 1.178
1/3
= 1.056 or 5.6% per quarter.
Therefore, in quarter 1, the forecast for actual sales = 5,300 × 1.056 × 0.6 = 3,358.
(2) The trend changes from 4,500 to 5,300. The growth rate is
500,4
300,5
= 1.178 = 17.8%.
Expressed per quarter (there are four quarters) this is 1.178
1/3
= 1.056 or 5.6% per quarter.
Therefore, in quarter 2, the forecast for actual sales = 5,300 × 1.056
2
× 0.4 = 2,364.

Answer bank 389
(3) The trend changes from 4,500 to 5,300. The growth rate is
500,4
300,5
= 1.178 = 17.8%.
Expressed per quarter (there are four quarters) this is 1.178
1/3
= 1.056 or 5.6% per quarter.
Therefore, in quarter 3, the forecast for actual sales = 5,300 × 1.056
3
× 1.2 = 7,489.
(4) The trend changes from 4,500 to 5,300. The growth rate is
500,4
300,5
= 1.178 = 17.8%.
Expressed per quarter (there are four quarters) this is 1.178
1/3
= 1.056 or 5.6% per quarter.
Therefore, in quarter 4, the forecast for actual sales = 5,300 × 1.056
4
× 1 = 6,591.
96 (a) A =
944
B =
962
C =
236.0
D =
240.5
E =
238
F =
–114
Workings
Moving Moving
total of average of
4 quarters' 4 quarters' Seasonal
Year Quarter Sales sales sales Trend variation
20X2 1 200
2 110
870 217.5
3 320 219 +101
884 221.0
4 240 222 +18
892 223.0
20X3 1 214 225 -11
906 226.5
2 118 229 -111
926 231.5
3 334 232 +102
932 233.0
4 260 234 +26
938 234.5
20X4 1 220 235 -15
944 236.0
2 124 238 –114
962 240.5
3 340
4 278
A = 260 + 220 + 124 + 340 = 944
