Choudhry. Fixed Income Securities Derivatives Handbook

Подождите немного. Документ загружается.

202 Selected Cash and Derivative Instruments

After calculating the prices for the conventional element of the callable

bond, the next step is to compute the value of the option element. On the

bond’s maturity date, the option is worthless, because its “strike” is 100,

which is the price the bond is redeemed at in any case. The option needs

to be valued, however, at all the other node points.

The holder of the option in the case of a callable bond is the issuing

company. At each call date during the life of the bond, the option holder

will elect either to exercise it or to wait till the next date. In making this

decision, the option holder must consider the following factors:

❑ the value of holding the option for an extra period, denoted by

❑ the value of exercising the option straight away, P

If P

is greater than P

, the holder will not exercise; if P

is greater

than P

, the holder will exercise immediately. The general rule determin-

ing whether P

or P

is greater is that options have more value “alive than

dead.” The same is true for callable bonds. It is sometimes more advanta-

geous to run an in-the-money option rather than exercise straight away.

On the other hand, at the year 2.5 call date, there is no value in holding

the option for another period because it will be worthless at year 3. There-

fore, if the option is in the money, the holder will exercise.

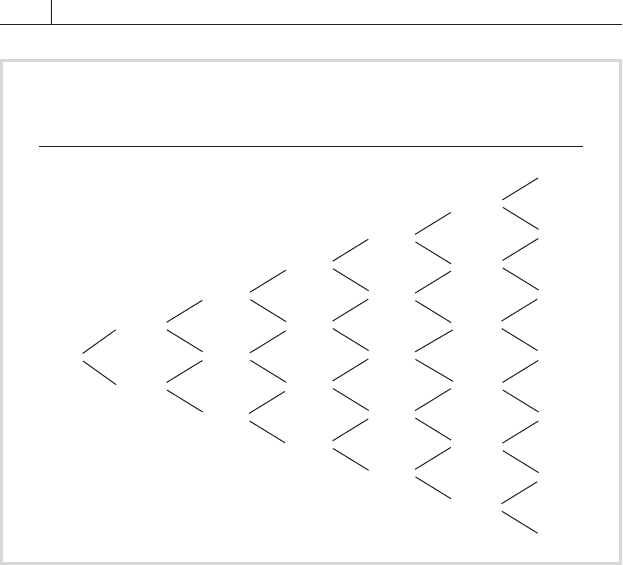
FIGURE 11.10

The Binomial Price Tree for the Hypothetical

3-Year 6 Percent Bond, Ignoring the Call Provision

105.875

103.671

105.564

101.607

103.437

104.997

100.102

101.684

103.018

104.121

99.113

100.445

101.337

102.086

102.951

99.142

99.794

100.323

100.857

101.302

101.774

100.00

The Analysis of Bonds with Embedded Options 203

A number of factors dictate whether an option is exercised or not. The

ﬁ rst is the asymmetric proﬁ t-loss proﬁ le of option holders: their potential gain

is theoretically unlimited when the price of the “underlying” asset rises, but

they lose only their initial investment if the price falls. This asymmetry favors

running an option position. Another consideration favoring holding is the

fact that the option’s time value is lost if it is exercised early. In callable bonds,

the call price often decreases as the bond approaches maturity. This creates

an incentive to delay exercise until a lower strike price is available. Coupon

payments, on the other hand, may favor earlier exercise, since, in the case of a

normal, nonembedded option, this allows the holder to earn interest sooner.

The general process of valuing embedded options works as follows: say

the value of the option for immediate exercise is V

, the value of the option

held for a further period is V

, and the value of the option at any node is V.

These values are deﬁ ned by equations (11.9), (11.10), and (11.11).

05 05

(11.9)

where

= the value of the option in the up state

t = the value of the option in the down state

r = the six-month interest rate at the speciﬁ ed node

VPS

=−

()

max ,0

(11.10)

where

P = the bond’s value at the speciﬁ ed node

S = the call option strike price, determined by the call schedule

VVV

()

max , .

(11.11)

The option value binomial tree, shown in

FIGURE 11.11, is constructed

by applying the appropriate expressions at each node, starting at the ﬁ nal

period and working backward in time.

It is now possible to complete the price tree for the callable bond. Re-

member that the option in the case of a callable bond is held by the issuer.

Its value, given by the tree in ﬁ gure 11.11, must therefore be subtracted

from the conventional bond price, given by the tree in ﬁ gure 11.10, to ob-

tain the callable bond value. For instance, the current price of the callable

bond is 105.875 – 0.76, or 105.115.

FIGURE 11.12 shows the tree that

results from this process. A tree constructed in this way, which is program-

mable into a spreadsheet or as a front-end application, can be used to price

either a callable or a putable bond.

204 Selected Cash and Derivative Instruments

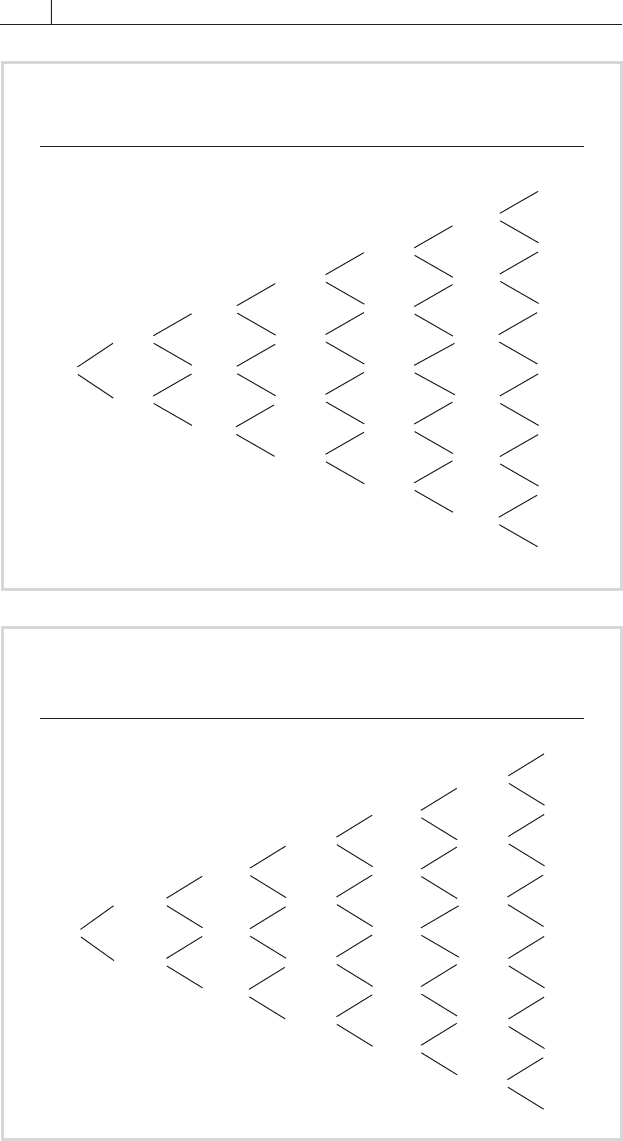
FIGURE 11.11

Binomial Price Tree for the Option Embedded

in the Callable 3-Year 6 Percent Bond

0.76

0.31

1.24

0.00

0.44

2.00

0.00

1.02

2.12

0.00

0.59

1.45

0.00

0.30

0.77

0.00

FIGURE 11.12

Binomial Price Tree for the Hypothetical Callable

3-Year 6 Percent Bond

105.12

103.361

104.324

101.607

102.997

100.102

101.684

101.998

102.001

99.113

100.445

101.337

101.500

99.142

99.794

100.323

100.857

101.002

101.004

100.00

The Analysis of Bonds with Embedded Options 205

Price and Yield Sensitivity

As explained in chapter 1, the curve representing a plain vanilla bond’s

price-yield relationship is essentially convex. The price-yield curve for a

bond with an embedded option changes shape as the bond’s price ap-

proaches par, at which point the bond is said to exhibit negative convexity.

This means that its price will rise by a smaller amount for a decline in yield

than it will fall for a rise in yield of the same magnitude.

FIGURE 11.13

summarizes the price-yield relationships for both negatively and positively

convex bonds.

Callable bonds exhibit negative convexity as interest rates fall. Option-

adjusted spread analysis highlights this relationship by effecting a parallel

shift in the benchmark yield curve, holding the spread constant, and cal-

culating the theoretical prices along the nodes of the binomial price tree.

The average present value is the projected price for the bond.

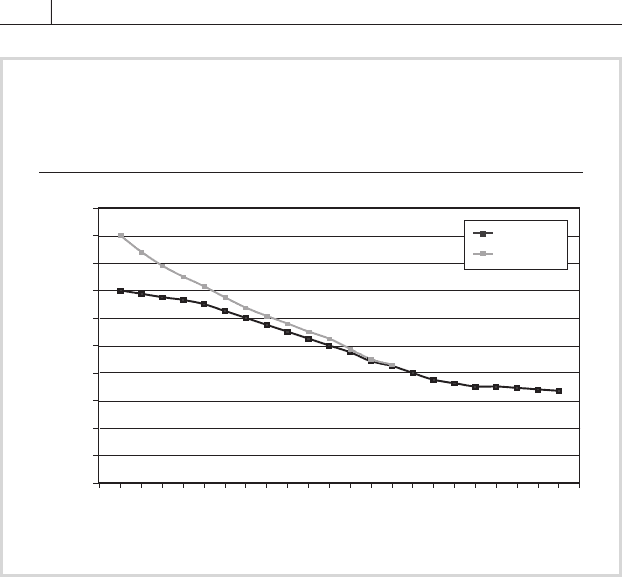
FIGURE 11.14

shows how this process affects the price-yield relationship of a hypotheti-

cal callable bond by comparing it with that of a conventional bond having

the same coupon and maturity. Note that once the market rate falls below

10 percent, the callable bond exhibits negative convexity. This is because

the embedded option is exercisable at that point, effectively capping the

bond’s price.

The market quotes bonds with embedded options in terms of yield

spreads. A “cheap” bond trades at a high spread, a “dear” one at a low

spread. The usual convention is to quote the spread between the redemp-

tion yield of the bond being analyzed and that of a government bond

having an equivalent maturity. This is not an accurate measure of the

actual difference in value between the two bonds, however. The reason is

that, as explained in chapter 1, the redemption yield computation unreal-

istically discounts all a bond’s cash ﬂ ows at a single rate.

A better measure of the relative value of a bond with an embedded

FIGURE 11.13 Price-Yield Relationships Associated with

Negative and Positive Convexity

PERCENT PRICE CHANGE FOR

CHANGE IN YIELD POSITIVE CONVEXITY NEGATIVE CONVEXITY

Fall of 100 bp X% Lower than Y%

Rise of 100 bp Lower than X% Y%

206 Selected Cash and Derivative Instruments

option is the constant spread that, when added to all the short-rates in

the binomial tree, makes the bond’s theoretical (model-derived) price

equal to its observed market price. The constant spread that satisﬁ es this

requirement is the option-adjusted spread. It is “option-adjusted” because

it reﬂ ects the option feature attached to the bond.

The OAS depends on the volatility level assumed in applying the

model. For a given price, the higher the speciﬁ ed volatility, the lower the

spread for a callable bond and the higher the spread for a putable one.

Since the OAS is usually calculated relative to a government spot- or

forward-rate curve, it reﬂ ects the credit and liquidity premiums over the

government bond that are assigned to the corporate bond. OAS analysis

depends on the valuation model being used and is only as accurate as the

model itself.

Measuring Bond Yield Spreads

The binomial model evaluates a bond’s return by measuring the extent to

which it exceeds those determined by the risk-free short rates in the tree.

The spread between these returns is the bond’s incremental return at a

speciﬁ ed price. Determining the spread involves the following steps:

❑ the binomial tree is used to derive a theoretical price for the bond

FIGURE 11.14

Projected Prices for Callable and Conventional

Bonds with Identical Coupons and Final Maturity

Dates

Benchmark yield (%)

Projected bond price

Callable

Noncallable

100

102

104

106

108

110

2 4 6 8 10 12 14

The Analysis of Bonds with Embedded Options 207

❑ this theoretical price is compared with the bond’s observed market

price

❑ if the two prices differ, the rates in the binomial model are adjusted

by a user-speciﬁ ed amount, which is the estimated spread

❑ a new theoretical price is derived using the adjusted rates and com-

pared with the observed one

❑ the previous two steps are repeated until the two prices are the

same

Price Volatility of Bonds with Embedded Options

As explained in chapter 2, the duration for any bond may be calculated

using equation (11.12) (assuming annualized yields).

()

∑

(11.12)

where

= the bond cash ﬂ ow at time t

P = the bond’s fair price

C = the annual coupon payment

rm = the redemption yield

n = the number of years to maturity

To calculate the modiﬁ ed duration of a bond with an embedded op-

tion, the bondholder must assume a ﬁ xed maturity date based on the

bond’s current price. When it is unclear what redemption date to use,

modiﬁ ed duration may be calculated to both the ﬁ rst call date and the

ﬁ nal maturity date. This is an unsatisfactory compromise, however, since

neither date, and so neither measure, may be appropriate. The problem is

more acute for bonds that are continuously callable or putable from the

ﬁ rst call or put date until maturity.

Effective Duration

It is possible to overcome some of the drawbacks of traditional duration

by using OAS analysis to derive a bond’s effective duration. As will be dis-

cussed in chapter 14, effective duration is based on approximate duration.

Following Fabozzi (1997), approximate duration is derived using equation

(11.13).

Prm

approx

−

()

−+

∆

(11.13)

208 Selected Cash and Derivative Instruments

where

= the initial price of the bond

= the estimated price of the bond if the yield falls by

∆rm

= the estimated price of the bond if the yield rises by

∆rm

= the change in the yield of the bond

Effective duration recognizes that yield changes may effect the future

cash ﬂ ow of a bond and so its price. For bonds with embedded options

the difference between traditional duration and effective duration can be

signiﬁ cant. The effective duration of a callable bond, for example, is some-

times half its traditional duration. As noted in chapter 14, for mortgage-

backed securities, the difference is sometimes greater still.

Effective duration may be calculated using the binomial model and

equation (11.13), as follows:

❑ calculate the bond’s OAS spread

❑ apply a downward parallel shift to the benchmark yield

❑ construct an adjusted binomial tree using the new yield curve

❑ add the OAS adjustment to the short rate at each of the tree’s

nodes

❑ use the modiﬁ ed binomial tree—shown in Figure 11.9—to calcu-

late the new value of the bond

❑ substitute this new price for P

in equation (11.13)

The same steps are used to derive P

, except that the yield curve is shifted

upward instead of downward. The effective duration of bonds containing

embedded options is often referred to as option-adjusted spread duration.

This measure has two advantages. The ﬁ rst is that it takes into account the

interest-rate-dependent behavior of the embedded option and thus of the

bond’s cash ﬂ ows. This is done by incorporating the binomial tree and hold-

ing the bond’s OAS constant over the speciﬁ ed interest rate shifts, in effect

maintaining the credit spread demanded by the market. The second, and

possibly more signiﬁ cant, advantage is that OAS duration is based on a par-

allel shift in the benchmark yield curve and so links changes in a bond’s price

to changes in market interest rates rather than to shifts in its own yield.

Effective Convexity

Just as standard duration is not appropriate for bonds with embedded op-

tions, neither is traditional convexity. This is because traditional convexity,

like traditional duration, fails to take into account the impact on a bond’s

future cash ﬂ ows of a change in market interest rates. As discussed in chap-

ter 14, the approximate convexity of any bond may be derived, following

in Fabozzi (1997), using equation (11.14).

The Analysis of Bonds with Embedded Options 209

PP P

Prm

+−

()

+−

∆

(11.14)

If the prices used for P

, P

, and P

are calculated assuming that the

bond’s remaining cash ﬂ ows will not change when market rates do, the

convexity computed is for an option-free bond. For bonds with embedded

options, the prices used in the equation should be derived using a bino-

mial model, in which the cash ﬂ ows do change with interest rates. The

result is effective or option-adjusted convexity.

Sinking Funds

In some markets, most prominently in the United States, corporate bond

issuers set up sinking fund provisions. A sinking fund allows the issuer to

redeem the principal using one of two methods: by purchasing the stipu-

lated amount of bonds in the open market and delivering them to the

trustee for cancellation or by calling the required amount of the bonds at

par. The second option is, in effect, a partial call—that is, a call involving

only a fraction of the issue. The bonds called are generally selected ran-

domly, by certiﬁ cate serial numbers.

The method the issuer chooses to fulﬁ ll the sinking fund requirement

is a function of the interest rate level. If interest rates have risen since the

bond was issued, depressing the bond’s price, the issuer will purchase the

required amount of bonds in the open market. If interest rates have fallen,

it will call the speciﬁ ed amount at par. As an illustration, consider the hy-

pothetical ABC bond whose terms are listed in

FIGURE 11.15.

According to the terms in ﬁ gure 11.15, the ABC bond pays an

8 percent coupon and is set to mature in 2019. It also contains a provision

stating that the issuer will redeem $50 million of the bond’s $100 million

FIGURE 11.15 A Hypothetical Bond with a Sinking Fund

Issuer ABC plc

Issue date 1–Dec–99

Maturity date 1–Dec–19

Nominal $5 million

Coupon 8%

Sinking fund provision $5 million December 1, 2009 to 2018

210 Selected Cash and Derivative Instruments

face value over ten years. This is the formal provision. The actual payments

made may differ.

ABC has in effect embedded ten European options in the bond, each

relating to $5 million nominal of the bonds and each expiring on December

1 of a different year, starting in 2009 and ending with 2018. The decision to

exercise the options as they mature is made using the binomial-tree method

discussed earlier.

211

CHAPTER 12

Inﬂ ation-Indexed Bonds

ertain countries have markets in bonds whose coupon or ﬁ nal

redemption payment, or both, are linked to their consumer price

indexes. Generally, the most liquid markets in these inﬂ ation-

indexed, or index-linked, debt instruments are the ones for government

issues. Investors’ experiences with the bonds differ, since the securi-

ties were introduced at different times in different markets and so are

designed differently. In some markets, for instance, only the coupon

payment, and not the redemption value, is index-linked. This makes

comparisons in terms of factors such as yield difﬁ cult and has in the

past hindered arbitrageurs seeking to exploit real yield differences. This

chapter highlights the basic concepts behind indexed bonds and how

their structures may differ from market to market.

Basic Concepts

The features considered in the design of index-linked bonds are the

type of index, the indexation lag, the coupon frequency, and the type

of indexation.

Choice of Index

In principle, bonds can be linked to almost any variable, including vari-

ous price indexes, earnings measures, GDP output, speciﬁ c commodities,

and the exchange rate of foreign currencies against another currency.

Ideally, the chosen index should reﬂ ect the hedging requirements of both