Choudhry. Fixed Income Securities Derivatives Handbook

Подождите немного. Документ загружается.

122 Selected Cash and Derivative Instruments

Swaptions

A bank or corporation may buy or sell an option on a swap, known as a

swaption. The buyer of a swaption has the right, but not the obligation, to

transact an interest rate swap during the life of the option. An option on

a swap where the buyer is the ﬁ xed-rate payer is termed a call swaption;

one where the buyer becomes the ﬂ oating-rate payer is a put swaption. The

writer of the swaption becomes the buyer’s counterparty in underlying the

transaction.

Swaptions are similar to forward-start swaps, except that the buyer can

choose not to commence payments on the effective date. A bank may pur-

chase a call swaption if it expects interest rates to rise; it will exercise only

if rates do indeed rise. A company may use swaptions to hedge future in-

terest rate exposures. Say it plans to take out a ﬁ ve-year bank loan in three

months. This transaction will make the company liable for ﬂ oating-rate

interest payments, which are a mismatch for the ﬁ xed-rate income it earns

on the long-term mortgages on its books. To correct this mismatch, the

company intends to transact a swap in which it receives LIBOR and pays

ﬁ xed after getting the loan. To hedge against an unforeseen rise in interest

rates in the meantime, which would increase the swap rate it has to pay, it

may choose to purchase an option, expiring in three months, on a swap in

which it pays a ﬁ xed rate of, say, 10 percent.

If the 5-year swap rate is above 10 percent in three months, after the

company has taken out its loan, it will exercise the swaption. If the rate

is below 10 percent, however, it will transact the swap in the normal way,

and the swaption will expire worthless. The swaption thus enables a com-

pany to hedge against unfavorable movements in interest rates but also to

gain from favorable ones. There is, of course, a cost associated with this

beneﬁ t: the swaption premium.

Valuation

Since a ﬂ oating-rate bond is valued on its principal value at the start of a

swap, a swaption may be viewed as the value on a ﬁ xed-rate bond, with a

strike price that is equal to the face value of the ﬂ oating-rate bond.

Swaptions are typically priced using the Black-Scholes or the Black

pricing model. With a European swaption, the appropriate swap rate on

the expiry date is assumed to be lognormal. The swaption payoff is given

by equation (7.19).

Payoff =−

()

max , 0

(7.19)

Swaps 123

where

= the strike swap rate

r = the actual swap rate at expiry

n = the swap’s term

M = the notional principal

F = the swap payment frequency

The Black model uses equation (7.20) to derive the price of an interest

rate option.

cPTfNd XNd=

()

−

()

⎡

⎣

⎢

⎤

⎦

⎥

01 2

(7.20)

where

c = the price of the call option

P (t, T ) = the price at time t of a zero-coupon bond maturing at time T

f = the forward price of the underlying asset with maturity T

= the forward price at time t

X = the strike price of the option

N = normal distribution

and where

fX T

()

+ln / /σ

fX T

()

−

=−

ln / /σ

and

σ = the volatility of f

Equation (7.20) can be combined with (7.19) to form (7.21), which

derives the value of a swap cash ﬂ ow received at time t

PtfNd rNd

01 2

() ()

−

()

⎡

⎣

⎢

⎤

⎦

⎥

(7.21)

where

= the forward swap rate at time 0

= the continuously compounded zero-coupon interest rate for an

instrument with maturity t

From (7.21), equation (7.22) can be constructed to derive the total

value of the swaption.

124 Selected Cash and Derivative Instruments

PtfNd rNd

() ()

−

()

⎡

⎣

⎢

⎤

⎦

⎥

∑

01 2

(7.22)

Interest Rate Swap Applications

This section discusses how swaps are used to hedge bond instruments and

how swap books are themselves hedged.

Corporate and Investor Applications

As noted earlier, swaps can be tailored to suit a user’s requirements. For ex-

ample, swaps’ payment dates, payment frequencies, and LIBOR margins

are often speciﬁ ed to match customers’ underlying exposures. Because the

market is so large, liquid, and competitive, banks are willing to structure

swaps to meet the requirements of virtually all customers, although smaller

customers may have difﬁ culty obtaining competitive quotes for notional

values below $10 million.

FIGURE 7.6

Excel Formulae for Figure 7.5

CELL C D E F

21 10000000

23 PERIOD ZERO-COUPON RATE % DISCOUNT FACTOR FORWARD RATE %

24 1 5.5 0.947867298 5.5

25 2 6 0.88999644 “((E24/E25)-1)*100

26 3 6.25 0.833706493 “((E25/E26)-1)*100

27 4 6.5 0.777323091 “((E26/E27)-1)*100

28 5 7 0.712986179 “((E27/E28)-1)*100

“SUM(E24:E28)

Swaps 125

In terms of their applications, swaps generally fall into two categories:

those linked to assets and those linked to liabilities. An asset-linked swap

is used by investors to change the characteristics of the income stream

generated by an asset, such as a bond. Liability-linked swaps are used by

borrowers to change the pattern of their cash ﬂ ows. Of course, the assign-

ment of a swap to one of these categories depends on the point of view of

the assignor. What is an asset-linked swap for one party is a liability-linked

hedge for the counterparty, except in the case of market-making banks

that make two-way quotes on the instruments.

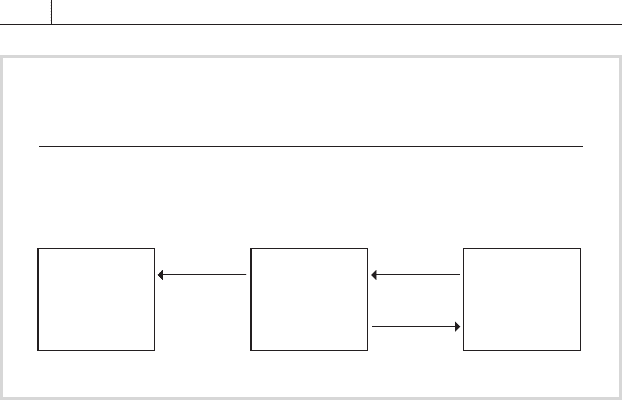
One straightforward application of an interest rate swap is to convert

a ﬂ oating-rate liability into a ﬁ xed-rate one, usually in an effort to remove

exposure to upward moves in interest rates. Say a company has borrowed

money at a ﬂ oating rate of 100 basis points over 6-month LIBOR. Fear-

ing that interest rates will rise in the three years remaining on the loan, it

enters into a 3-year semiannual interest rate swap with a bank, depicted

FIGURE 7.7 on the following page, in which it pays a ﬁ xed rate of 6.75

percent and receives 6-month LIBOR. This ﬁ xes the company’s borrowing

costs for three years at 6.75 percent plus 100 basis points, or 7.75 percent,

for an effective annual rate of 7.99 percent.

G H I J

FIXED PAYMENT FLOATING PAYMENT PV FIXED PAYMENT PV FLOATING PAYMENT

689,625 “(F24*10000000)/100 “G24/1.055 “H24/(1.055)

689,625 “(F25*10000000)/100 “G24/(1.06)^2 “H25/(1.06)^2

689,625 “(F26*10000000)/100 “G24/(1.0625)^3 “H26/(1.0625^3)

689,625 “(F27*10000000)/100 “G24/(1.065)^4 “H27/(1.065)^4

689,625 “(F28*10000000)/100 “G24/(1.07)^5 “H28/(1.07)^5

2,870,137 2,870,137

126 Selected Cash and Derivative Instruments

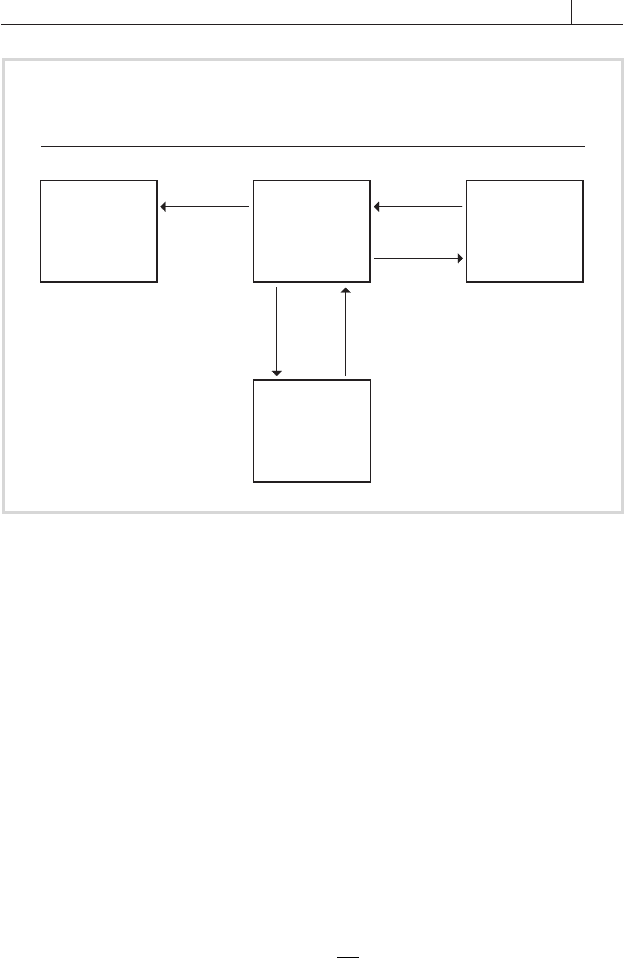
Say a corporation borrows funds for ﬁ ve years at a rate of 6.25

percent. Shortly after taking out the loan, it enters into a swap in

which it pays a ﬂ oating rate of LIBOR and receives 5.85 ﬁ xed (see

FIGURE 7.8). Its net borrowing cost is thus LIBOR plus 40 basis points

(6.25 minus 5.85). After one year, interest rates have fallen, and the

4-year swap rate is quoted at 4.90–84 percent—that is, banks are willing

to receive 4.90 or pay 4.84 ﬁ xed. The company decides to take advantage

of the lower interest rates by switching back to a ﬁ xed-rate liability. To

this end, it enters into a second swap in which it pays 4.90 percent ﬁ xed

and receives LIBOR. Its borrowing cost is now 5.30 percent (4.90 plus

40 basis points), or 95 basis points—the difference between the two swap

rates—below its original borrowing cost.

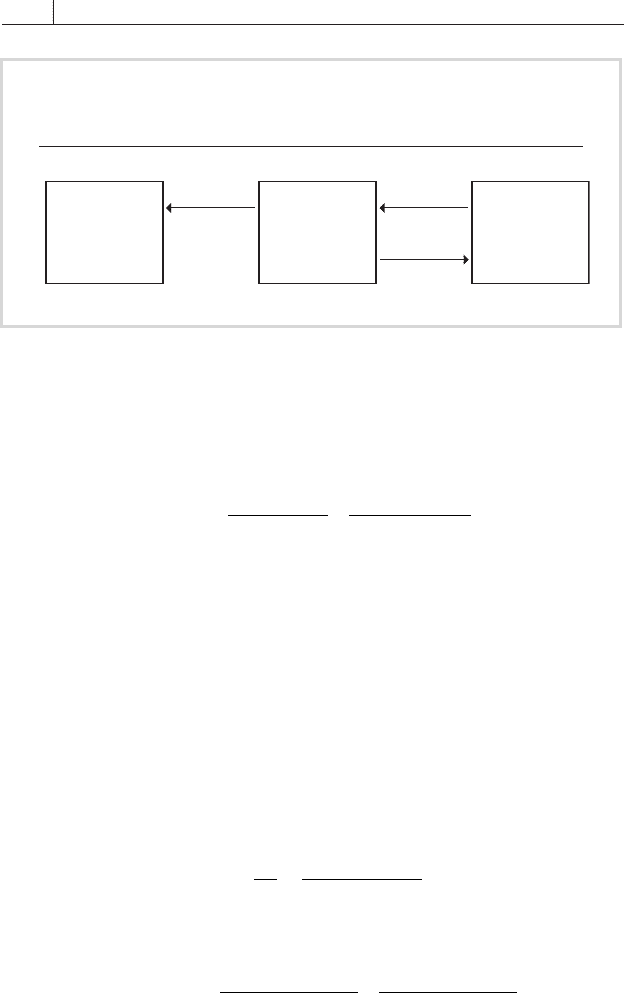
Investors might use asset-linked swaps if they want ﬁ xed-rate securi-

ties, and the only assets available with the required credit quality and

terms pay ﬂ oating rates. For instance, a pension fund may have invested

in 2-year ﬂ oating-rate gilts, an asset of the highest quality, that pay 5.5

basis points below the London interbank bid rate, or LIBID (the interest

rate at which a bank in the City of London is willing to borrow short

term from another City bank). As it is expecting interest rates to fall,

however, it prefers to receive a ﬁ xed rate. Accordingly, it arranges a tai-

lor-made swap in which it pays LIBID and receives a ﬁ xed rate of 5.50

percent. By entering into this swap, the pension fund creates a structure,

shown on page 128 in

FIGURE 7.9, that generates a ﬁ xed-income stream

of 5.375 percent.

FIGURE 7.7

Transforming a Liability from Fixed Rate to Floating

and Back to Fixed

Two-Swap Structure

LIBOR (L)

6.75%

L + 100bp

Bank Loan Company

Swap

Counterparty

Swaps 127

Hedging Bond Instruments Using Interest Rate Swaps

Bond traders wishing to hedge the interest rate risk of their bond posi-

tions have several tools to choose from, including other bonds, bond fu-

tures, and bond options, as well as swaps. Swaps, however, are particularly

efﬁ cient hedging instruments, because they display positive convexity. As

explained in chapter 2, this means that they increase in value when inter-

est rates fall more than they lose when rates rise by a similar amount—just

as plain vanilla bonds do.

The primary risk measure required when using a swap to hedge is the

present value of a basis point. PVBP, known in the U.S. market as the

dollar value of a basis point, or DVBP, indicates how much a swap’s value

will move for each basis point change in interest rates and is employed to

calculate the hedge ratio. PVBP is derived using equation (7.23).

PVBP

(7.23)

where

dS = change in swap value

dr = change in market interest rate, in basis points

It was suggested earlier that a swap be seen as a bundle of cash ﬂ ows

arising from the sale and purchase of two cash-market instruments: a

FIGURE 7.8

Swap Transforming a Floating-Rate Asset to a

Fixed-Rate One

5.85%

LIBOR

6.25%

4.90 LIBOR

Lenders Company

Second Swap

(4-year)

First Swap

(5-year)

128 Selected Cash and Derivative Instruments

ﬁ xed-rate bond with a coupon equal to the swap rate and a ﬂ oating-rate

bond with the same maturity and paying the same rate as the ﬂ oating

leg of the swap. Considering a swap in this way, equation (7.23) can be

rewritten as (7.24).

PVBP

=−

Fixed bond Floating bond

(7.24)

Equation (7.24) essentially states that PVBP of the swap equals the

difference between the PVBPs of the ﬁ xed- and ﬂ oating-rate bonds. This

value is usually calculated for a notional principal of $1 million, based on

the duration and modiﬁ ed duration of the bonds (deﬁ ned in chapter 2)

and assuming a parallel shift in the yield curve.

FIGURE 7.10 illustrates how the PVBP of a 5-year swap may be cal-

culated using the relationships expressed in (7.23) and (7.24). The two

derivations are shown in equations (7.25) and (7.26), respectively. (Bonds’

PVBPs can be calculated using Bloomberg’s YA screen or Microsoft Excel’s

MDURATION function.)

PVBP

swap

−−

()

4264 4236

425

(7.25)

PVBP PVBP PVBP

swap fixed floating

=−

−

1004940 9951171

1000640 999371

−

= 488.45-63.45

425.00=

(7.26)

FIGURE 7.9

Transforming a Floating-Rate Asset to a

Fixed-Rate One

5.50%

LIBIDLIBID–12.5

Gilt

Local

Authority

2-Year Swap

Swaps 129

Note that the swap PVBP, $425, is lower than that of the 5-year ﬁ xed-

coupon bond, which is $488.45. This is because the ﬂ oating-rate bond

PVBP reduces the risk exposure of the swap as a whole by $63.45. As a

rough rule of thumb, the PVBP of a swap is approximately the same as

that of a ﬁ xed-rate bond whose term runs from the swap’s next coupon

reset date through the swap’s termination date. Thus, a 10-year swap mak-

ing semiannual payments has a PVBP close to that of a 9.5-year ﬁ xed-rate

bond, and a swap with 5.5 years to maturity has a PVBP similar to that of

a 5-year bond.

One corollary of the relationship expressed in (7.25) is that swaps’

PVBPs behave differently from those of bonds. Immediately preceding

a reset date, when the PVBP of the ﬂ oating-rate bond corresponding to

the swap’s ﬂ oating leg is essentially nil, a swap’s PVBP is almost identical

to that of the ﬁ xed-rate bond maturing on the same day as the swap. For

example, if it’s a ﬁ ve-year swap, and it’s just before the second semiannual

payment, the PVBP will be similar to that of a four-year bond. Immedi-

ately after the reset date the swap’s PVBP will be nearly identical to that of

FIGURE 7.10

PVBPs of a 5-Year Swap and a Fixed-Rate Bond

with the Same Maturity Date

INTEREST RATE SWAP

Term to maturity 5 years

Fixed leg 6.50%

Basis Semi-annual, act/365

Floating leg 6-month LIBOR

Basis Semi-annual, act/365

Nominal amount $1,000,000

Present value $

Rate change – 10 bps 0 bps Rate change + 10 bps

Fixed-coupon bond 1,004,940 1,000,000 995,171

Floating-rate bond 1,000,640 1,000,000 999,371

Swap 4,264 0 4,236

130 Selected Cash and Derivative Instruments

a bond maturing at the next reset date. Therefore, from a point just before

the reset to one just after, the swap’s PVBP will decrease by the amount of

the ﬂ oating-rate PVBP. In between reset dates, the swap’s PVBP is quite

stable, since the effects of changes in the ﬁ xed- and ﬂ oating-rate PVBPs

cancel each other out. In contrast, a ﬁ xed-rate bond’s PVBP decreases

steadily over time, assuming that no sudden large-scale yield movements

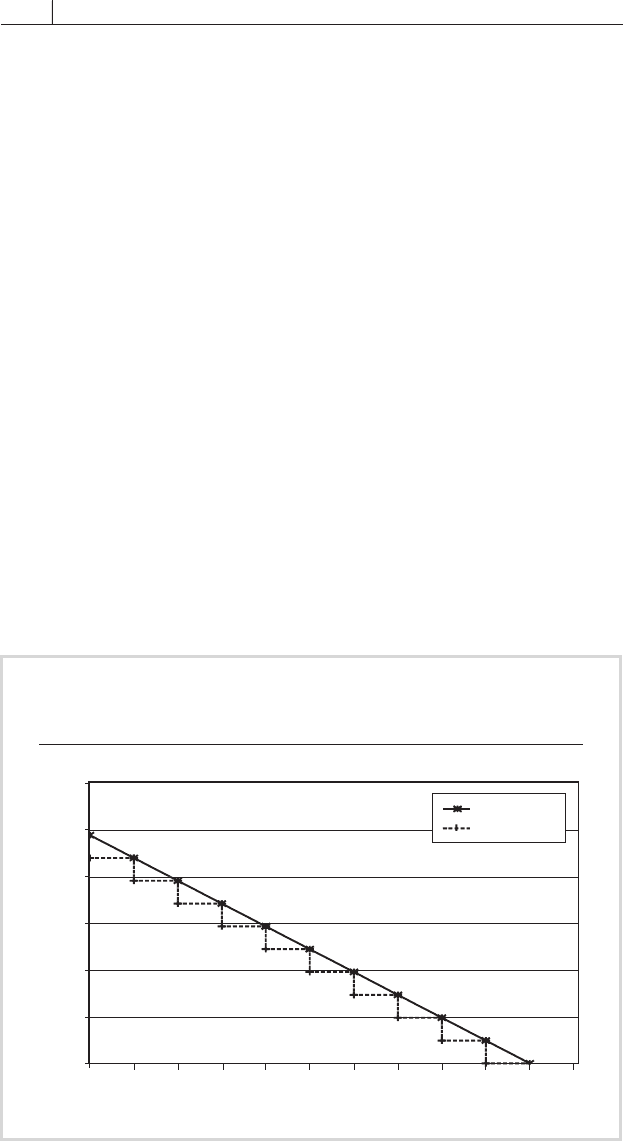
occur. The evolution of the swap and bond PVBPs is illustrated in

FIGURE

7.11

. Note that the graph does not reﬂ ect a slight anomaly that occurs in

the swap’s PVBP, which actually increases by a small amount between reset

dates because the ﬂ oating-rate bond’s PVBP decreases at a slightly faster

rate than that of the ﬁ xed-rate bond.

Hedging a bond with an interest rate swap is conceptually similar to

hedging it with another bond or with bond futures. Hedging a long posi-

tion in a vanilla bond requires a long position in the swap—that is, taking

the side that pays ﬁ xed and receives ﬂ oating. Hedging a short position in a

bond requires a short swap position, matching the ﬁ xed swap income with

the pay-ﬁ xed liability of the short bond position.

The swap’s value will change by approximately the same amount, but

in the opposite direction, as the bond’s value. The match will not be exact.

It is very difﬁ cult to establish a precise hedge for a number of reasons, in-

cluding differences in day count and in maturity, and basis risk. To mini-

mize the mismatch, the swap’s maturity should be as close as possible to

FIGURE 7.11

PVBP of a 5-Year Swap and Fixed-Rate Bond

Maturity Period

100

200

300

400

500

600

0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5

Time (years)

PVBP ($)

Fixed-rate bond

Swap

Swaps 131

the bond’s. Since swaps are OTC contracts, it should be possible to match

interest-payment dates as well as maturity dates.

The correct nominal amount of the swap is established using the

PVBP hedge ratio, shown as equation (7.27). Though the market still

uses this method, its assumption of parallel yield-curve shifts can lead to

signiﬁ cant hedging error.

Hedge ratio =

PVBP

bond

swap

(7.27)

Chapter Notes

1. The expression also assumes an actual/365 day count. If any other day-count conven-

tion is used, the 1/N factor must be replaced by a fraction whose numerator is the actual

number of days and whose denominator is the appropriate year base.

2. Zero-coupon and forward rates are also related in another way. If the zero-coupon rate

and the forward rate rf

are transformed to their continuously compounded equivalent

rates, ln(1 + rs

) and ln(1 + rf

), the result is the following expression, which derives the

continuously compounded zero-coupon rate as the simple average of the continuously

compounded forward rates:

−

∑