Cheban D.N. Global Attractors Of Non-autonomous Dissipative Dynamical Systems
Подождите немного. Документ загружается.


September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
Pullback attractors under discretization 337
(see Temam
[
314
]
, Chapter I.2.3). Assuming that p and r are differentiable functions
of R into itself, we can rewrite this system after the transformation u
3
:= u
3
−r(t)−
p(t) in the form (10.3) with the matrix
A(ω) =
−p(0) p(0) 0
−p(0) −1 0
0 0 −1
and the mapping
f(u, ω) =
0
−u
1
u
3
u
1
u
2
− ˙σ(0) − ˙r(0) − b(0)(r(0) + σ(0)) − (b(0) − 1)u
3
,
where u = (u
1
, u
2
, u
3
) and ω := ω(·) = (b(·), r(·), σ(·)) ∈ C(R, R) × C
1
(R, R) ×
C
1
(R, R).
Suppose that b is almost periodic in C(R, R) and that σ, r are almost periodic
in C
1
(R, R) with
0 < σ
min
:= inf
t∈R
σ(t), 1 < inf
t∈R
b(t).
Then define σ
t
for each t ∈ R by σ
t
p(·) := ω(· + t). Finally, define the parameter
set Ω to be the closed hull
[
292
]
P :=
[
t∈R
σ
t
(b(·), r(·), p(·)),
which is a compact subset of C(R, R) × C
1
(R, R) × C
1
(R, R).
We need to check that the assumptions D1–D4 are satisfied by the differential
equation with this matrix A and function f . The first assumption D1 follows
straighforwardly and the second D2 holds with α(ω) ≡ α
0
:= min(σ
min
, 1) > 0
with the assumptions on p and r ensuing the continuity of A. These assumptions
on p and r also ensure the continuity of f needed in D3 and the estimate is given
by
(f(u, ω), u) = (−˙p(0) − ˙r(0))u
3
−b(0)(r(0) + p(0))u
3
−(b(0) −1)u
2
3
≤
( ˙p(0) + ˙r(0))
2
2(b(0) − 1)
+
b
2
(0)(r(0) + p(0))
2
2(b(0) − 1)
=: c(ω)
with a(ω) ≡ 0. Finally, it is obvious from these definitions of the constants that
D4 is also satisfied, in particular with c
0
:= sup
ω∈Ω
c(ω) < ∞.

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
338 Global Attractors of Non-autonomous Dissipative Dynamical Systems
The Euler scheme for this differential equation also satisfies assumptions N1–
N4. Since F (h, u, ω) ≡ A(ω)u + f(u, ω) here, assumptions N3 and N4 hold triv-
ially, while assumption N1 follows from D1–D3 above. Assumption N2 also follows
from D1–D3 with the proof being almost the same as in the first part of the proof
in the Appendix. Note that if b is also assumed to be continuously differentiable,
then we have the usual second order local discretization error here. One can show
that assumptions N1–N4 are also satisfied by higher order schemes such as Runge–
Kutta schemes, but the details are not as straightforward or clean as for the Euler
scheme.
10.3 Cocycle property
The solution ϕ(t, u
0
, ω) of the differential equation (10.3) satisfies assumptions N1–
N4 the initial condition
ϕ(0, u
0
, ω) = u
0
for all (u
0
, ω) ∈ R
d
×Ω
and the cocycle property
ϕ(s + t, u
0
, ω) = ϕ(s, ϕ(t, u
0
, ω), σ
t
p) for all s, t ∈ R
+
, (u
0
, ω) ∈ R
d
×Ω
with respect to the autonomous dynamical system generated by the group {σ
t
}
t∈R
on Ω. (Existence of such solutions for all t ∈ R
+
is assured by that of an absorbing
set to be established in the proof of Theorem 10.2 below). By our assumptions the
mapping (t, u, ω) 7→ ϕ(t, u, σ
t
ω) is continuous. Moreover, the mapping ϕ := (ϕ, σ)
defined on R
+
×R
d
×Ω
ϕ(t, u, ω) := (ϕ(t, u, ω), σ
t
ω) for all (t, u
0
, ω) ∈ R
+
×R
d
×Ω
generates an autonomous semi-dynamical system, that is a skew product flow, on
the state space X := R
d
×Ω.
The situation is somewhat more complicated for the discrete time system gen-
erated by the numerical scheme with variable time steps. For this we will restrict
the choice of admissible step-size sequences. For each δ > 0, we define H
δ
to be the
set of all two sided sequences {h
n
}
n∈Z
satisfying
1
2
δ ≤ h
n
≤ δ (10.5)
for each n ∈ Z (the particular factor 1/2 here is chosen just for convenience). The
set H
δ
is compact metric space with the metric
ρ
H
δ
h
(1)
, h
(2)
=
∞
X
n=−∞
2
−|n|
h
(1)
n
−h
(2)
n
.
September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
Pullback attractors under discretization 339
We then consider the shift operator ˜σ : H
δ
→ H
δ
defined by ˜σh = ˜σ{h
n
}
n∈Z
:= {h
n+1
}
n∈Z
. The operator ˜σ is a homeomorphism with respect to the above
metric on H
δ
and its group of iterates {˜σ
n
}
n∈Z
forms a discrete time autonomous
dynamical system on the compact metric space
H
δ
, ρ
H
δ
. Finally, for a given
sequence {h
n
}
n∈Z
we set t
0
= 0 and define t
n
= t
n
(h) :=
P
n−1
j=0
h
j
and t
−n
=
t
−n
(h) := −
P
n
j=1
h
−j
for n ≥ 1.
Now we introduce the parameter space Q
δ
:= H
δ
×Ω for a fixed δ > 0 and we
use the following lemma to introduce a discrete time autonomous dynamical system
Θ = {Θ
n
}
n∈Z
on Q
δ
.
Lemma 10.1 The mappings Θ
n
: Q
δ
→ Q
δ
, n ∈ Z, generated by iteration of
Θ
0
:= id
Q
δ , Θ
1
(h, p) := (˜σ
1
h, σ
h
0
p) , Θ
−1
(h, p) :=
˜σ
−1
h, σ
−h
−1
p
form a group of continuous mappings on H
δ
×P .
Proof. We first show that Θ
1
Θ
−1
= Θ
−1
Θ
1
= Θ
0
= id
Q
δ . Indeed we have
Θ
1
Θ
−1
(h, p) = Θ
1
˜σ
−1
h, σ
h
−1
p
=
˜σ
1
˜σ
−1
h, σ
h
−1
σ
−h
−1
p
= (h, p)
Θ
−1
Θ
1
(h, p) = Θ
−1
(˜σ
1
h, σ
h
0
p) = (˜σ
−1
˜σ
1
h, σ
−h
0
σ
h
0
p) = (h, p).
The continuity of the Θ
n
mappings follows from the facts that (t, p) 7→ σ
t
p is
continuous, ˜σ is a homeomorphism and the composition and cartesian products of
continuous mappings are continuous.
We define a mapping ψ : Z
+
×R
d
×Q
δ
→ R
d
by
ψ(0, u
0
, q) := u
0
, ψ(n, u
0
, q) = ψ(n, u
0
, (h, p)) := u
n
n ≥ 1,
where u
n
is the nth iterate of the numerical scheme (10.4) with initial value u
0
∈
R
d
, initial parameter ω ∈ Ω and step-size sequence h ∈ H
δ
. These mappings are
continuous on R
d
×Q
δ
. They also satisfy a cocycle property with respect to Θ.
Lemma 10.2 ψ is a discrete time cocycle over (Q
δ
, Z, Θ) R
d
with fiber R
d
.
Proof. We write the numerical scheme (10.4) for a given (h, p) and u
0
as
u
n+1
= u
n
+ h
n
F
h
n
, σ
t
n
(h)
p, u
n
, n ∈ Z
+
,
where t
0
(h) = 0 and t
n
(h) =
P
n−1
j=0
h
j
for n ≥ 1. Hence, in terms of the ψ mapping
we have
ψ(n + 1, u
0
, (h, p)) = ψ(n, u
0
, (h, p)) + h
n
F (h
n
, σ
t
n
(h)
p, ψ(n, u
0
, (h, p)))
September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
340 Global Attractors of Non-autonomous Dissipative Dynamical Systems
in general and
ψ(1, u
0
, (h, p)) = u
0
+ h
0
F
h
0
, σ
t
0
(h)
p, u
0
)
for n = 0 since by definition ψ(0, u
0
, (h, p)) = u
0
, which gives the identity property.
The cocycle property is established as follows. Let n ≥ 0. Then
ψ(1 + n, u
0
, q) = ψ(1 + n, u
0
, (h, p))
= ψ(n, u
0
, (h, p)) + h
n
F
h
n
, σ
t
n
(h)
p, ψ(n, u
0
, (h, p))
= ψ(n, u
0
, (h, p)) + (˜σ
n
h)
0
F
(˜σ
n
h)
0
, σ
t
0
(˜σ
n
h)
p, ψ(n, u
0
, (h, p))
= ψ (1, p, Θ
n
(h), ψ(n, u
0
, (h, p))) = ψ (1, ψ(n, u
0
, q), Θ
n
q) ,
that is u
1+n
= = ψ (1, u
n
, Θ
n
q). Iterating this n times, we obtain
u
n
= ψ (1, u
0
, Θ
n−1
q) ◦··· ◦ψ (1, u
0
, Θ
0
q) .
Similarly with m ≥ 2 we have
ψ(m + n, u
0
, q) = u
m+n
= ψ (1, ·, Θ
m+n−1
q) ◦ ··· ◦ψ (1, ·, Θ
n
q) ◦
◦ψ (1, ·, Θ
n−1
q) ◦ ··· ◦ψ (1, u
0
, Θ
0
q)
= ψ (1, ·, Θ
m+n−1
q) ◦ ··· ◦ψ (1, u
n
, Θ
n
q)
= ψ (1, ·, Θ
m−1
Θ
n
q) ◦ ··· ◦ψ (1, u
n
, Θ
0
Θ
n
q)
= ψ (m, u
n
, Θ
n
q) = ψ (m, ψ (n, q, u
0
) , Θ
n
q) ,
which is the desired cocycle property.
Finally we define Ψ := (ψ, Θ) and observe that the mappings Ψ(n, ·.·) are con-
tinuous on R
d
×Q
δ
for n ∈ Z
+
.
Remark 10.4 The mappings ψ, Θ and Ψ are defined in the same way for each
δ > 0, so we do not index them with δ.
From the cocycle and group properties we obtain
Lemma 10.3 Ψ = (ψ, Θ) is a discrete time autonomous semi–dynamical system
on the state space R
d
×Q
δ
.

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
Pullback attractors under discretization 341
10.4 Main result
Our main result is the to establish the existence of pullback attractors for the
non-autonomous dynamical systems (NDS) generated by the differential equation
and numerical scheme and to show that the components of the numerical pullback
attractor are upper semi–continuous in their parameter and converge upper semi–
continuously to the corresponding components of the differential equation’s pullback
attractor. Global attractors also exist for the corresponding skew product flows and
converge upper semi–continuously in an appropriate sense.
Theorem 10.2 Let Assumptions D1–D4 and N1–N3 hold. Then the continuous
time NDS (ϕ, σ) generated by the differential equation (10.3) has a pullback attractor
I = {I
ω
| ω ∈ Ω} and the discrete time NDS (Ψ, Θ) generated by the numerical
scheme (10.4) has a pullback attractor I
δ
= {I
δ
q
| q ∈ Q
δ
}, provided the maximal
step-size δ is sufficiently small, such that the set-valued mappings ω 7→ I
ω
and (p, h)
7→ I
δ
(p,h)
are upper semi–continuous with respect to the Hausdorff semi-distance and
satisfy
lim
δ→0+
sup
h∈H
δ
β
I
δ
(ω,h)
, I
ω
= 0 for each ω ∈ Ω.
Moreover, the corresponding skew product flows have global attractors J and J
δ
,
respectively, of the form
J =
[
ω∈Ω
I
ω
×{ω}, J
δ
=
[
q∈Q
δ
I
δ
q
×{q},
which satisfy
lim
δ→0+
β
Pr
R
d
×Ω
J
δ
, J
= 0.
Proof. The proof of the convergence assertions in Theorem 10.2 will follow imme-
diately from an application of Theorem 10.1 after it has been shown that the ball
B[0; R
0
] in R
d
with centre 0 and radius R
0
:= 3
p
c
0
/α
0
is a forwards absorbing set
uniformly in all parameters for both the continuous time and discrete time cocycle
systems under consideration. The convergence assertions require additional work.
10.4.1 Existence of an absorbing set
Write x(t) for the solution ϕ(t, u
0
, ω) of (10.3), so
dx
dt
(t) = A(σ
t
ω)x(t) + f (σ
t
ω, x(t)).
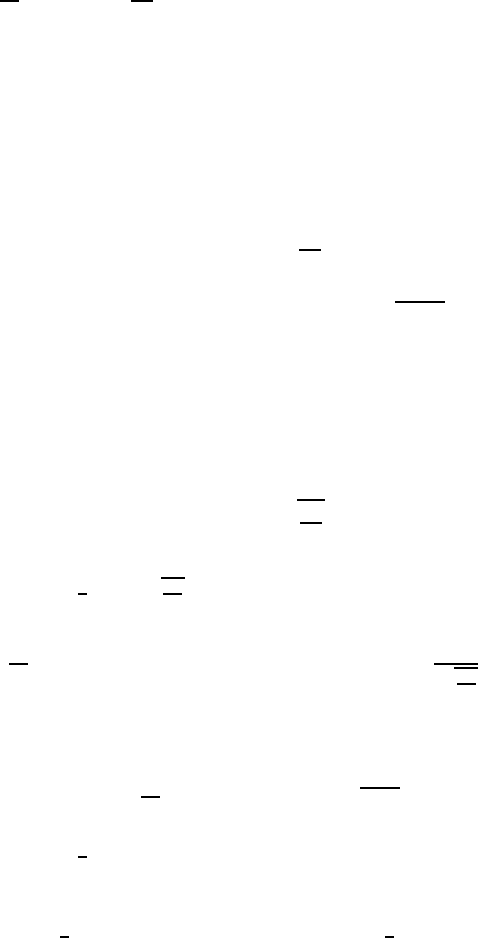
September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
342 Global Attractors of Non-autonomous Dissipative Dynamical Systems
The following estimate will also be used to construct an absorbing set.
d
dt
|x(t)|
2
= 2
dx
dt
(t), x(t)
= 2 (A(σ
t
p)x(t) + f(σ
t
p, x(t)), x(t)) (10.6)
= 2 (A(σ
t
p)x(t)) + 2 (f(σ
t
p, x(t)), x(t))
≤ −2α(σ
t
p) |x(t)|
2
+ 2a(σ
t
p) |x(t)|
2
+ 2c(σ
t
p)
≤ −2 (α(σ
t
p) − a(σ
t
p)) |x(t)|
2
+ 2c
0
≤ −2α
0
|x(t)|
2
+ 2c
0
and so
|x(t)|
2
≤ |u
0
|
2
e
−2α
0
t
+
c
0
α
0
1 − e
−2α
0
t
.
This implies that the ball B[0; R
0
] with radius R
0
= 3
p
c
0
/α
0
is a forwards absorb-
ing and positively invariant set for all solutions of the differential equation (10.3)
uniformly in ω ∈ Ω. Note for later purposes that the ball B[0; 2R
0
/3] is also posi-
tively invariant for the differential equation.
The proof that B[0; R
0
] is a uniform forwards absorbing set for the numerical
scheme (10.4) is more complicated. First we show that the inequality (10.6) implies
|x(t)| ≤ |u
0
|e
−α
0
t
+
r
c
0
α
0
1 − e
−α
0
t
. (10.7)
as long as |x(t)| ≥
1
3
R
0
=
q
c
0
α
0
. To see this note that (10.6) can be rewritten as
d
dt
|x(t)|
2
≤ −2α
0
|x(t)|
2
+ 2c
0
≤ −2α
0
|x(t)|
2
+ 2
c
0
q
c
0
α
0
|x(t)|
and hence as
d
dt
|x(t)| ≤ −α
0
|x(t)| +
√
c
0
α
0
as long as |x(t)| ≥
1
3
R
0
.
We note also by continuity that there exists a T = T (c
0
, α
0
) > 0 such that |x(t)|
= |ϕ(t, u
0
, ω)| ≥
1
3
R
0
for all t ∈ [0, T ], u
0
with |u
0
| ≥
2
3
R
0
and ω ∈ Ω.
We fix an R R
0
and let K
R
be the constant in the local discretization
error estimate for the ball B[0; R]. Then from (10.7) with x(h) = ϕ(h, u
0
, ω) and
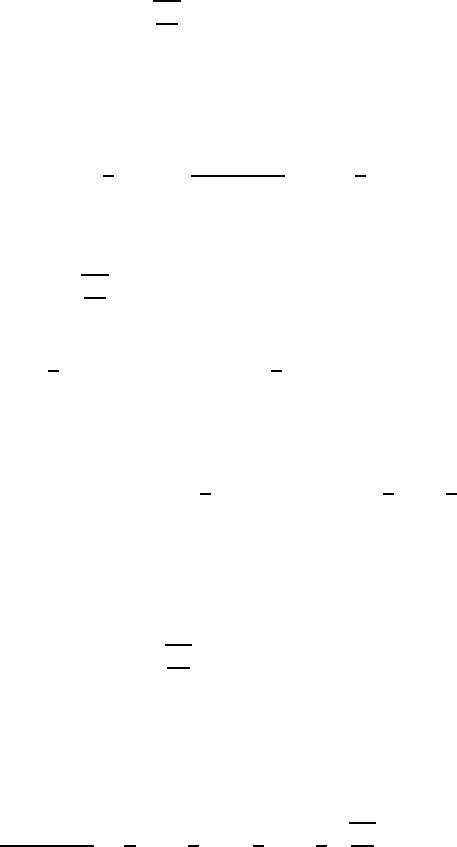
September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
Pullback attractors under discretization 343
Assumption N2 we have
|u
1
| ≤ |ϕ(h, u
0
, ω)|+ |ϕ(h, u
0
, ω) − u
1
|
≤ |u
0
|e
−α
0
h
+
r
c
0
α
0
1 − e
−α
0
h
+ K
R
hµ
R
(h) (10.8)
for u
0
∈ A[R, 2R
0
/3] := B[0; R] \B[0; 2R
0
/3] and h ∈ (0, T ]. Now let δ
0
∈ (0, 1] ∩
(0, T ] be such that
K
R
hµ
R
(h) ≤
1
3
R
0
,
K
R
hµ
R
(h)
1 − e
−α
0
h
≤ R −
1
3
R
0
for h ∈ (0, δ
0
]. Then from (10.8) for u
0
∈ A[R, 2R
0
/3] and h ∈ (0, δ
0
] we have
|u
1
| ≤ |u
0
|e
−α
0
h
+
r
c
0
α
0
1 − e
−α
0
h
+ K
R
hµ
R
(h)
≤ Re
−α
0
h
+
1
3
R
0
1 − e
−α
0
h
+
R −
1
3
R
0
1 − e
−α
0
h
≤ R,
so u
1
∈ B[0; R]. In addition, for u
0
∈ B[0; 2R
0
/3] we have x(h) ∈ B[0; 2R
0
/3], so
|u
1
| ≤ |ϕ(h, u
0
, ω)|+ |ϕ(h, u
0
, ω) − u
1
| ≤
2
3
R
0
+ K
R
hµ
R
(h) ≤
2
3
R
0
+
1
3
R
0
= R
0
for h ∈ (0, δ
0
], so u
1
∈ B[0; R] here too. Hence, the ball B[0; R] is positively invariant
for the numerical scheme for u
0
∈ B[0; R] and h ∈ (0, δ
0
]. We can thus apply the
inequality (10.8) iteratively as long as the u
n
∈ A[R, 2R
0
/3], that is we have
|u
n+1
| ≤ |u
n
|e
−α
0
h
+
r
c
0
α
0
1 − e
−α
0
h
+ K
R
hµ
R
(h) (10.9)
when u
0
, u
1
, . . ., u
n
∈ A[R, 2R
0
/3] and h ∈ (0, δ
0
].
Now further restrict the step-size so that
K
R
hµ
R
(h)
1 − e
−α
0
h
≤
1
2
R
0
−
1
3
R
0
=
1
2
R
0
−
1
2
r
c
0
α
0
for all h ∈ (0, δ
1
], where δ
1
∈ (0, δ
0
). Using a similar argument as above for the ball
B[0; R], we can show that the ball B[0; R
0
] is positively invariant for the numerical
scheme with step-sizes h ∈ (0, δ
1
].
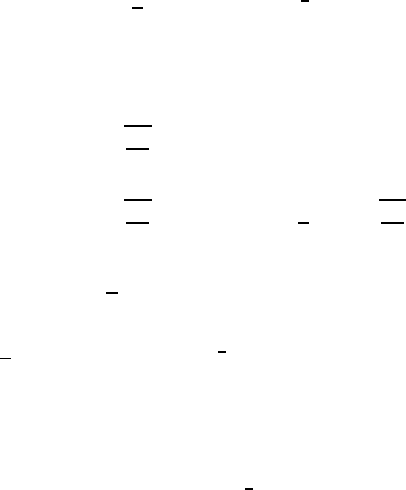
September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
344 Global Attractors of Non-autonomous Dissipative Dynamical Systems
To show that the ball B[0; R
0
] is absorbing, we further restrict the step-size so
that
1
2
1 + e
−α
0
h
≤ e
−
1
4
α
0
h
for all h ∈ (0, δ
2
], where δ
2
∈ (0, δ
1
]. Then, if u
0
∈ A[R, R
0
], from inequality (10.9)
we have
|u
1
| ≤ |u
0
|e
−α
0
h
+
r
c
0
α
0
1 − e
−α
0
h
+ K
R
hµ
R
(h)
≤ |u
0
|e
−α
0
h
+
r
c
0
α
0
1 − e
−α
0
h
+
1
2
R
0
−
r
c
0
α
0
1 − e
−α
0
h
≤ |u
0
|e
−α
0
h
+
1
2
|u
0
|
1 − e
−α
0
h
≤
1
2
1 + e
−α
0
h
|u
0
| ≤ e
−
1
4
α
0
h
|u
0
|.
In particular, when u
0
, u
1
, . . ., u
j
∈ B[0; R] \ B[0; R
0
] we can iterate the last
inequality to obtain
|u
j
| ≤ e
−j
1
8
α
0
δ
|u
0
|
if we use variable step-sizes with δ/2 ≤ h
j
δ with δ ∈ (0, δ
2
]. Obviously, there
exists a finite integer J
R
(u
0
) such that |u
j
| ≤ R
0
for all j ≥ J
R
(u
0
), that is the ball
B[0; R
0
] is absorbing for the numerical scheme for all step-size sequences h ∈ H
δ
with δ ∈ (0, δ
2
]. Note that this holds uniformly in ω ∈ Ω.
10.4.2 Upper semi–continuity of the pullback attractor component
sets
Let ψ(n, x, q) denote the numerical trajectory and Θ the shift operator on Q
δ
. The
mappings q 7→ Θq and (x, q) 7→ ψ(n, x, q) for each integer positive n are continuous.
The absorbing set B = B[0; R
0
] is compact absorbing set and forwards in-
variant uniformly in q ∈ Q
δ
. Hence, by the cocycle property, the compact sets
ψ(n, B, Θ
−n
q) are nested with increasing n and the pullback attractor has compo-
nent sets defined by
I
δ
q
:=
\
n≥0
ψ(n, B, Θ
−n
q)
September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
Pullback attractors under discretization 345
This means, in particular, that β(ψ(n, B, Θ
−n
q), I
δ
q
) → 0 as n → ∞. Let ε > 0 and
pick n
0
= n
0
(ε, q) > 0 so that
ψ(n
0
, B, Θ
−n
0
q) ⊂ B
I
δ
q
, ε
,
where B
I
δ
q
, ε
is the ball of radius ε about I
δ
q
.
Now the compact set-valued mappings q 7→ ψ(n, B, Θ
−n
q) are continuous in q
with respect to the Hausdorff semi-distance for each fixed n. Fix ε > 0 and pick n
0
= n
0
(ε, ¯q) from above. Then there exists δ(ε, ¯q) = δ(ε, n
0
(ε, ¯q)) > 0 such that
β (ψ(n
0
, B, Θ
−n
0
q), ψ(n
0
, B, Θ
−n
0
¯q)) < ε
for all q ∈ Q
δ
with ρ(q, ¯q) < δ(ε, ¯q). In particular,
ψ(n
0
, B, Θ
−n
0
q) ⊂ B (ψ(n
0
, B, Θ
−n
0
¯q), ε)
for all q ∈ Q
δ
with ρ
Q
δ (q, ¯q) < δ(ε, ¯q). Hence we have
I
δ
q
⊂ ψ(n
0
, B, Θ
−n
0
q) ⊂ B (ψ(n
0
, B, Θ
−n
0
¯q), ε)
⊂ B
B
I
δ
¯q
, ε
, ε
= B
I
δ
¯q
, 2ε
that is I
δ
q
⊂ B
I
δ
¯q
, 2ε
or equivalently β
I
δ
q
, I
δ
¯q
< 2ε for all q ∈ Q
δ
with ρ(q, ¯q) <
δ(ε, ¯q). This means the mapping q 7→ I
δ
q
is upper semi–continuous.
The proof for the mapping ω 7→ A
ω
is essentially the same.
10.4.3 Upper semi–continuous convergence of the discretized
pullback attractors
We will now prove the upper semi–continuous convergence of the discretized pull-
back attractor component sets to their continuous time counterparts. For the proof
we need the following lemma on the convergence of the numerical trajectories to the
corresponding continuous time trajectory with convergence of the maximum step
size to zero. Its proof is given in the appendix.
Lemma 10.4 For fixed t > 0 and h = {h
n
}
n∈Z
∈ H
δ
for some δ > 0, let N(t, h)
be the positive integer such that
h
−1
+ h
−2
+ ··· + h
−N(t,h)
≤ t < h
−1
+ h
−2
+ ··· + h
−N(t,h)−1

September 27, 2004 16:46 WSPC/Book Trim Size for 9.75in x 6.5in GlobalAttractors/chapter 10
346 Global Attractors of Non-autonomous Dissipative Dynamical Systems
and consider a sequence (of step-size sequences) with h
m
∈ H
δ
m
, where δ
m
→ 0 as
m → ∞. Then
ψ
N(t, h
m
), u
m
, Θ
−N(t,h
m
)
(h
m
, ω
m
)
→ ϕ(t, u
0
, σ
−t
ω) as m → ∞
for any sequence u
m
→ u
0
∈ R
d
and ω
m
→ ω ∈ Ω.
We suppose that the upper semi–continuous convergence assertion of Theorem
10.2 is not true. Then there exists an ε
0
> 0 and sub-sequences (for convenience
we use the original index) h
m
in H
δ
m
and a
m
∈ I
δ
m
(ω,h
m
)
for m ∈ N such that
dist
a
m
, I
(ω,0)
≥ ε
0
. (10.10)
Note that the component sets I
(ω,h)
and A
δ
q
are contained in the ball B[0; R
0
] where
R
0
= 3
p
c
0
/α
0
for each ω ∈ Ω. Then a
m
∈ A
δ
m
(p,h
m
)
⊂ B[0; R
0
] for each for m ∈
N and B[0; R
0
] is compact, so there exists a convergent subsequence (again we use
the original index) a
m
→ a
∗
∈ B[0; R
0
]. Thus we have
dist
a
∗
, I
(ω,0)
≥ ε
0
.
Now choose t > 0 sufficiently large so that by pullback attraction
dist
ϕ (t, σ
−t
p, B[0; R
0
]) , I
(ω,0)
<
1
2
ε
0
. (10.11)
By the invariance property of a pullback attractor there exist b
m
∈ A
δ
m
Θ
−N(t,h
m
)
(ω,h
m
)
such that
ψ
N(t, h
m
), Θ
−N(t,h
m
)
(p, h
m
), b
m
= a
m
. (10.12)
Since the A
δ
m
Θ
−N(t,h
m
)
(ω,h
m
)
⊂ B[0; R
0
] for each for m ∈ N, there exists a convergent
subsequence (once again we use the original index) b
m
→ b
∗
∈ B[0; R
0
]. By (10.12)
and Lemma 10.4 we have
ϕ (t, σ
−t
ω, b
∗
) = a
∗
,
which contradicts (10.10) with respect (10.11). This contradiction proves the upper
semi–continuous convergence of the numerical pullback attractor components.
10.4.4 Upper semi–continuous convergence of the discretized
global attractors
Let J ⊆ R
d
× Ω be the global attractor of the continuous time skew prod-
uct flow dynamical system π(t, u, ω) = (ϕ(t, u, ω), σ
t
ω) and J
δ
⊂ H
δ
× R
d
× Ω
the global attractor of the discrete time semi–dynamical system π
δ
(n, h, u, ω) =
