Бушев В.А. В. Теоретические процессы бытовых машин и приборов
Подождите немного. Документ загружается.

ɧɢɢ ɥɸɦɢɧɟɫɰɟɧɬɧɵɯ ɫɜɟɬɢɥɶɧɢɤɨɜ 300ɥɤ, ɞɥɹ ɡɚɥɨɜ – 200ɥɤ, ɞɥɹ ɫɩɚɥɶɧɵɯ
ɤɨɦɧɚɬ – 75ɥɤ. ɉɪɢ ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɥɚɦɩ ɧɚɤɚɥɢɜɚɧɢɹ ɷɬɢ ɰɢɮɪɵ ɞɨɥɠɧɵ
ɛɵɬɶ ɭɦɟɧɶɲɟɧɵ ɜɞɜɨɟ.
ɉɪɢ ɫɨɫɬɚɜɥɟɧɢɢ ɬɟɩɥɨɜɨɝɨ ɛɚɥɚɧɫɚ ɩɨɦɟɳɟɧɢɹ ɫɥɟɞɭɟɬ ɭɱɢɬɵɜɚɬɶ,
ɱɬɨ ɨɫɜɟɳɟɧɢɟ ɨɛɵɱɧɨ ɞɟɣɫɬɜɭɟɬ ɬɨɥɶɤɨ ɱɚɫɬɶ ɫɭɬɨɤ ɢ, ɤɚɤ
ɩɪɚɜɢɥɨ, ɬɟɩɥɨɩɨɫɬɭɩɥɟɧɢɹ ɨɬ ɧɟɝɨ ɧɟ ɫɨɜɩɚɞɚɸɬ ɜɨ ɜɪɟɦɟɧɢ ɫ ɩɨɫɬɭɩɥɟɧɢɟɦ
ɬɟɩɥɚ ɨɬ ɫɨɥɧɟɱɧɨɣ ɪɚɞɢɚɰɢɢ.
ɉɪɢɦɟɪ ɪɚɫɱɟɬɚ: ɩɨɦɟɳɟɧɢɹ ɚɭɞɢɬɨɪɢɢ (5·10·3)
F=2(5·10)+2(3·5)+2(3·10)=100+30+60=190 ɦ
2
Q
ɨɫɜ
=200·190·0.1·0.55=2090 ȼɬ.
Ɍɟɩɥɨɩɪɢɬɨɤɢ ɱɟɪɟɡ ɧɚɪɭɠɧɵɟ ɨɝɪɚɠɞɟɧɢɹ ɫ ɭɱɟɬɨɦ ɫɨɥɧɟɱɧɨɣ ɪɚɞɢɚɰɢɢ
ɉɪɢ ɫɨɫɬɚɜɥɟɧɢɢ ɬɟɩɥɨɜɨɝɨ ɛɚɥɚɧɫɚ ɩɨɦɟɳɟɧɢɹ ɞɥɹ ɬɟɩɥɨɝɨ ɩɟɪɢɨɞɚ ɝɨɞɚ
ɧɟɨɛɯɨɞɢɦɨ ɪɚɫɫɱɢɬɚɬɶ ɩɟɪɟɞɚɱɭ ɬɟɩɥɨɬɵ ɱɟɪɟɡ ɧɚɪɭɠɧɵɟ ɨɝɪɚɠɞɟɧɢɹ ɫ ɭɱɟɬɨɦ
ɞɟɣɫɬɜɢɹ ɫɨɥɧɟɱɧɨɣ ɪɚɞɢɚɰɢɢ.
Ⱦɥɹ ɥɟɬɧɢɯ ɫɭɬɨɤ ɯɚɪɚɤɬɟɪɧɵ ɡɧɚɱɢɬɟɥɶɧɵɟ ɤɨɥɟɛɚɧɢɹ ɬɟɦɩɟɪɚɬɭɪɵ
ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ ɢ ɢɧɬɟɧɫɢɜɧɨɫɬɢ ɫɨɥɧɟɱɧɨɣ ɪɚɞɢɚɰɢɢ, ɩɨɞɚɸɳɟɣ ɧɚ
ɨɝɪɚɠɞɟɧɢɹ ɡɞɚɧɢɹ. ɉɨɫɬɭɩɥɟɧɢɟ ɬɟɩɥɚ ɭɫɬɚɧɚɜɥɢɜɚɸɬ ɞɥɹ ɠɚɪɤɢɯ ɥɟɬɧɢɯ
ɫɭɬɨɤ. ɉɨɥɚɝɚɸɬ, ɱɬɨ ɬɟɦɩɟɪɚɬɭɪɚ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ ɢɡɦɟɧɹɟɬɫɹ ɩɨ
ɝɚɪɦɨɧɢɱɟɫɤɨɦɭ ɡɚɤɨɧɭ ɫ ɫɭɬɨɱɧɵɦ ɩɟɪɢɨɞɨɦ. Ɇɚɤɫɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ
ɬɟɦɩɟɪɚɬɭɪɵ Ⱥ
tɧ
,t
ɧ
– ɫɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ. Z
tɧ
ɦɚɯ
=15 ɱɚɫ. (ɜɪɟɦɹ ɦɚɤɫɢɦɭɦɚ
ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɵ).
ȼɥɢɹɧɢɟ ɫɨɥɧɟɱɧɨɝɨ ɨɛɥɭɱɟɧɢɹ ɨɝɪɚɠɞɟɧɢɣ ɭɱɢɬɵɜɚɟɬɫɹ ɞɨɛɚɜɥɟɧɢɟɦ ɤ
t
ɧ
ɷɤɜɢɜɚɥɟɧɬɧɨɣ ɬɟɦɩɟɪɚɬɭɪɧɨɣ ɞɨɛɚɜɤɢ ¨t
ɪ
¨t
ɪ
=ɪq/Į
ɧ
, ɝɞɟ q- ɪɚɞɢɚɰɢɨɧɧɚɹ ɩɥɨɬɧɨɫɬɶ ɬɟɩɥɨɜɨɝɨ ɩɨɬɨɤɚ; ɪ –
ɤɨɷɮɮɢɰɢɟɧɬ ɩɨɝɥɨɳɟɧɢɹ ɫɨɥɧɟɱɧɨɣ ɪɚɞɢɚɰɢɢ ɩɨɜɟɪɯɧɨɫɬɶɸ ɨɝɪɚɠɞɟɧɢɹ; Į
ɧ
–
ɤɨɷɮɮɢɰɢɟɧɬ ɬɟɩɥɨɨɬɞɚɱɢ ɧɚ ɧɚɪɭɠɧɨɣ ɩɨɜɟɪɯɧɨɫɬɢ ɨɝɪɚɠɞɟɧɢɹ.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, t
ɭɫɥ
=t
ɧ
+¨t
ɪ
– ɭɫɥɨɜɧɚɹ ɫɪɟɞɧɹɹ ɬɟɦɩɟɪɚɬɭɪɚ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ.
ɇɚɪɭɠɧɵɟ ɨɝɪɚɠɞɟɧɢɹ ɩɨɦɟɳɟɧɢɣ ɦɨɝɭɬ ɛɵɬɶ ɦɚɫɫɢɜɧɵɦɢ
ɧɟɩɪɨɡɪɚɱɧɵɦɢ (ɫɬɟɧɵ, ɩɟɪɟɤɪɵɬɢɹ) ɢ ɥɭɱɟɩɪɨɡɪɚɱɧɵɦɢ (ɨɤɧɚ, ɜɢɬɪɢɧɵ); ɱɟɪɟɡ
ɦɚɫɫɢɜɧɵɟ ɨɝɪɚɠɞɟɧɢɹ ɜɧɟɲɧɢɟ ɬɟɩɥɨɜɵɟ ɜɨɡɞɟɣɫɬɜɢɹ ɩɟɪɟɞɚɸɬɫɹ
ɢɡɦɟɧɟɧɧɵɦɢ ɩɨ ɜɟɥɢɱɢɧɟ ɢ ɫ ɡɚɩɚɡɞɵɜɚɧɢɟɦ ɜɨ ɜɪɟɦɟɧɢ. ɑɟɪɟɡ ɩɪɨɡɪɚɱɧɵɟ
ɨɝɪɚɠɞɟɧɢɹ ɫɨɥɧɟɱɧɚɹ ɪɚɞɢɚɰɢɹ ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɨ ɩɪɨɧɢɤɚɟɬ ɜ ɩɨɦɟɳɟɧɢɟ ɢ
ɩɟɪɟɞɚɱɚ ɬɟɩɥɚ ɩɪɨɢɫɯɨɞɢɬ ɩɪɚɤɬɢɱɟɫɤɢ ɛɟɡ ɡɚɩɚɡɞɵɜɚɧɢɹ.
ɋɪɟɞɧɟɟ ɩɨɫɬɭɩɥɟɧɢɟ ɬɟɩɥɨɬɵ ɱɟɪɟɡ ɦɚɫɫɢɜɧɨɟ ɨɝɪɚɠɞɟɧɢɟ ɨɩɪɟɞɟɥɹɟɬɫɹ
ɩɨ ɭɪɚɜɧɟɧɢɸ ɬɟɩɥɨɩɟɪɟɞɚɱɢ:
Q
1
=k
1
·F
1
·(t
ɭɫɥ
-t
ɜ
),
ɝɞɟ k
1
– ɤɨɷɮɮɢɰɢɟɧɬ ɬɟɩɥɨɩɟɪɟɞɚɱɢ,
F
1
– ɩɥɨɳɚɞɶ ɨɝɪɚɠɞɟɧɢɹ,
t
ɜ
– ɬɟɦɩɟɪɚɬɭɪɚ ɜɨɡɞɭɯɚ ɩɨɦɟɳɟɧɢɹ.
ɉɨɫɬɭɩɥɟɧɢɟ ɬɟɩɥɨɬɵ ɱɟɪɟɡ ɩɪɨɡɪɚɱɧɵɟ ɨɝɪɚɠɞɟɧɢɹ (ɨɤɧɚ, ɜɢɬɪɢɧɵ)
ɩɪɨɢɫɯɨɞɢɬ ɤɚɤ ɡɚ ɫɱɟɬ ɬɟɩɥɨɩɟɪɟɞɚɱɢ Q
2ɬ
, ɬɚɤ ɢ ɡɚ ɫɱɟɬ ɢɡɥɭɱɟɧɢɹ Q
2ɪ
. ɋɪɟɞɧɟɟ
ɡɧɚɱɟɧɢɟ ɬɟɩɥɨɜɨɝɨ ɩɨɬɨɤɚ ɱɟɪɟɡ ɩɪɨɡɪɚɱɧɵɟ ɨɝɪɚɠɞɟɧɢɹ ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɩɨ
ɮɨɪɦɭɥɟ:
Q
2
=Q
2ɬ
+Q
2ɪ
=k
2
·F
2
·(t
ɧ.ɭɫɥ
-t
ɜ
)+ȕ
1
·ȕ
2
·F
2
·q
0
,

ɝɞɟ k
2
– ɤɨɷɮɮɢɰɢɟɧɬ ɬɟɩɥɨɩɟɪɟɞɚɱɢ ɞɥɹ ɨɤɧɚ,
F
2
– ɟɝɨ ɩɥɨɳɚɞɶ ɩɨɜɟɪɯɧɨɫɬɢ,
ȕ
1
ɢȕ
2
– ɤɨɷɮɮɢɰɢɟɧɬɵ ɩɪɨɧɢɤɧɨɜɟɧɢɹ ɢ ɡɚɬɟɧɟɧɢɹ ɨɤɧɚ ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ,
q
0
– ɫɪɟɞɧɹɹ ɡɚ ɫɭɬɤɢ ɢɧɬɟɧɫɢɜɧɨɫɬɶ ɫɨɥɧɟɱɧɨɣ ɪɚɞɢɚɰɢɢ.
Ⱦɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɧɚɢɛɨɥɶɲɟɝɨ ɩɨɫɬɭɩɥɟɧɢɹ ɬɟɩɥɨɬɵ ɧɟɨɛɯɨɞɢɦɨ ɜ
ɮɨɪɦɭɥɚɯ ɛɪɚɬɶ ɦɚɤɫɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɬɟɦɩɟɪɚɬɭɪɵ t
ɧ.ɭɫɥ
ɢ ɦɚɤɫɢɦɚɥɶɧɨɟ
ɡɧɚɱɟɧɢɟ ɬɟɩɥɨɜɨɝɨ ɩɨɬɨɤɚ ɨɬ ɪɚɞɢɚɰɢɢ q ɜɦɟɫɬɨ q
0
. ɉɪɢ ɷɬɨɦ ɦɨɠɧɨ ɭɱɟɫɬɶ,
ɱɬɨ ɧɚɢɛɨɥɶɲɟɟ ɡɧɚɱɟɧɢɟ ɫɪɟɞɢ Q
1
, Q
2ɬ
ɢ Q
2ɪ
ɢɦɟɟɬ Q
2ɪ
.
Ɍɟɩɥɨɩɨɫɬɭɩɥɟɧɢɹ ɨɬ ɥɸɞɟɣ
Ɍɟɩɥɨɩɨɫɬɭɩɥɟɧɢɟ ɨɬ ɥɸɞɟɣ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɮɨɪɦɭɥɟ:
Q
ɥ
=N·Q
ɱ
,
ɝɞɟ N- ɤɨɥɢɱɟɫɬɜɨ ɥɸɞɟɣ ɜ ɩɨɦɟɳɟɧɢɢ; Q
ɱ
– ɬɟɩɥɨɜɨɣ ɩɨɬɨɤ ɨɬ ɱɟɥɨɜɟɤɚ.
Q
ɱ
ɢɦɟɟɬ ɞɜɟ ɫɨɫɬɚɜɥɹɸɳɢɟ:
Q
ɱ.ɥ.
- ɹɜɧɭɸ ɬɟɩɥɨɬɭ ɡɚ ɫɱɟɬ ɢɡɥɭɱɟɧɢɹ ɢ ɤɨɧɜɟɤɰɢɢ ɢ Q
ɱ.ɫɤɪ
- ɫɤɪɵɬɭɸ
ɬɟɩɥɨɬɭ ɡɚ ɫɱɟɬ ɢɫɩɚɪɹɸɳɟɣ ɜɥɚɝɢ ɫ ɩɨɜɟɪɯɧɨɫɬɢ ɬɟɥɚ ɢ ɥɟɝɤɢɯ ɱɟɥɨɜɟɤɚ,
ɬ.ɟ.
Q
ɱ
=Q
ɱ.ɥ
+Q
ɱ.ɫɤɪ
ɉɨɥɧɨɟ ɤɨɥɢɱɟɫɬɜɨ ɜɵɞɟɥɹɟɦɨɝɨ ɱɟɥɨɜɟɤɨɦ ɬɟɩɥɚ ɡɚɜɢɫɢɬ ɨɬ ɬɨɝɨ, ɤɚɤɨɣ
ɢɧɬɟɧɫɢɜɧɨɫɬɢ ɮɢɡɢɱɟɫɤɭɸ ɪɚɛɨɬɭ ɜɵɩɨɥɧɹɟɬ ɱɟɥɨɜɟɤ ɢ ɨɬ ɬɨɝɨ, ɤɚɤɨɜɚ
ɬɟɦɩɟɪɚɬɭɪɚ ɩɨɦɟɳɟɧɢɹ ɢ ɤɚɤɨɜɵ ɬɟɩɥɨɡɚɳɢɬɧɵɟ ɫɜɨɣɫɬɜɚ ɨɞɟɠɞɵ.
Ɋɚɫɱɟɬ ɹɜɧɨɝɨ ɬɟɩɥɚ ɩɪɨɜɨɞɹɬ ɩɨ ɷɦɩɢɪɢɱɟɫɤɨɣ ɮɨɪɦɭɥɟ:
Q
ɱ.ɥ
=ȕ
ɢ
ȕ
ɨɞ
(2.5+10.3
ȼ
V )(35-t
ɩ
),
ɝɞɟ ȕ
ɢ
– ɤɨɷɮɮɢɰɢɟɧɬ, ɭɱɢɬɵɜɚɸɳɢɣ ɢɧɬɟɧɫɢɜɧɨɫɬɶ ɪɚɛɨɬɵ;
ȕ
ɨɞ
– ɤɨɷɮɮɢɰɢɟɧɬ, ɭɱɢɬɵɜɚɸɳɢɣ ɬɟɩɥɨɡɚɳɢɬɧɵɟ ɫɜɨɣɫɬɜɚ ɨɞɟɠɞɵ;
V
ɜ
– ɫɤɨɪɨɫɬɶ ɞɜɢɠɟɧɢɹ ɜɨɡɞɭɯɚ ɜ ɩɨɦɟɳɟɧɢɢ; t
ɩ
– ɬɟɦɩɟɪɚɬɭɪɚ ɩɨɦɟɳɟɧɢɹ
Ǻ
ɨɞ
=0.65 – ɞɥɹ ɨɛɵɱɧɨɣ ɨɞɟɠɞɵ; 0.4 – ɞɥɹ ɭɬɟɩɥɟɧɧɨɣ ɨɞɟɠɞɵ.
ȼɥɚɝɨɜɵɞɟɥɟɧɢɹ ɢ ɩɨɥɧɵɟ ɬɟɩɥɨɜɵɞɟɥɟɧɢɹ ɨɬ ɱɟɥɨɜɟɤɚ
Ʉɚɬɟɝɨɪɢɹ ɮɢɡɢɱɟɫɤɨɣ
ɪɚɛɨɬɵ
ȕ
ɩ
ȼɥɚɝɨɜɵɞɟɥɟɧɢɹ,
ɝ/ɱ
ɉɨɥɧɵɟ ɬɟɩɥɨɜɵɞɟɥɟɧɢɹ,
ȼɬ.
ɋɨɫɬɨɹɧɢɟ ɩɨɤɨɹ
—
30 - 115 93 – 140
Ʌɟɝɤɚɹ
1 40 - 200 140 – 175
ɋɪɟɞɧɟɣ ɬɹɠɟɫɬɢ
1.07 70 - 280 175 – 290
Ɍɹɠɟɥɚɹ
1.15 135 - 415 >290
Ȼɨɥɶɲɢɟ ɡɧɚɱɟɧɢɹ ɜɥɚɝɨɜɵɞɟɥɟɧɢɹ ɢ ɦɟɧɶɲɢɟ ɡɧɚɱɟɧɢɹ ɬɟɩɥɨɜɵɞɟɥɟɧɢɣ
ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɜɵɫɨɤɨɣ ɬɟɦɩɟɪɚɬɭɪɟ ɩɨɦɟɳɟɧɢɹ (~35˚ɋ), ɰɢɮɪɵ ɜɬɨɪɨɣ
ɝɪɚɧɢɰɵ ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɧɢɡɤɨɣ ɬɟɦɩɟɪɚɬɭɪɟ ɩɨɦɟɳɟɧɢɹ ~10˚ɋ.
2. Ɇɟɬɨɞɢɱɟɫɤɨɟ ɩɨɫɨɛɢɟ ɞɥɹ ɩɪɚɤɬɢɱɟɫɤɢɯ ɪɚɛɨɬ ɩɨ ɞɢɫɰɢɩɥɢɧɟ
«Ɍɟɨɪɟɬɢɱɟɫɤɢɟ ɩɪɨɰɟɫɫɵ ɛɵɬɨɜɵɯ ɦɚɲɢɧ ɢ ɩɪɢɛɨɪɨɜ»
Ɂɚɤɪɟɩɥɟɧɢɟ ɬɟɨɪɟɬɢɱɟɫɤɨɝɨ ɦɚɬɟɪɢɚɥɚ ɞɢɫɰɢɩɥɢɧɵ ɩɪɨɜɨɞɢɬɫɹ ɧɚ ɩɪɚɤɬɢɱɟɫɤɢɯ ɢ
ɥɚɛɨɪɚɬɨɪɧɵɯ ɡɚɧɹɬɢɹɯ. Ʉɪɨɦɟ ɥɟɤɰɢɣ ɞɥɹ ɭɝɥɭɛɥɟɧɧɨɝɨ ɢɡɭɱɟɧɢɹ ɬɟɨɪɢɢ ɫɬɭɞɟɧɬɭ
ɪɟɤɨɦɟɧɞɭɟɬɫɹ ɭɱɟɛɧɚɹ ɥɢɬɟɪɚɬɭɪɚ, ɩɪɟɞɫɬɚɜɥɟɧɧɚɹ ɜ ɛɢɛɥɢɨɝɪɚɮɢɱɟɫɤɨɦ ɫɩɢɫɤɟ
ɩɨɫɨɛɢɹ. Ɍɚɤ ɤɚɤ ɱɢɫɥɨ ɚɭɞɢɬɨɪɧɵɯ ɢ ɩɪɚɤɬɢɱɟɫɤɢɯ ɡɚɧɹɬɢɣ ɨɝɪɚɧɢɱɟɧɨ, ɫɬɭɞɟɧɬɭ
ɫɥɟɞɭɟɬ ɞɨɩɨɥɧɢɬɟɥɶɧɨ ɜ ɯɨɞɟ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨɣ ɪɚɛɨɬɵ ɩɪɨɪɚɛɚɬɵɜɚɬɶ ɢɡɭɱɟɧɧɵɣ
ɬɟɨɪɟɬɢɱɟɫɤɢɣ ɦɚɬɟɪɢɚɥ. ɋ ɷɬɨɣ ɰɟɥɶɸ ɜɨ ɜɬɨɪɨɣ ɱɚɫɬɢ ɩɨɫɨɛɢɹ ɩɨɞɨɛɪɚɧɵ ɡɚɞɚɱɢ,
ɫɝɪɭɩɩɢɪɨɜɚɧɧɵɟ ɩɨ ɨɫɧɨɜɧɵɦ ɪɚɡɞɟɥɚɦ ɞɢɫɰɢɩɥɢɧɵ. Ʉɚɠɞɵɣ ɢɡ ɪɚɡɞɟɥɨɜ ɧɚɱɢɧɚɟɬɫɹ ɫɨ
ɫɜɨɞɤɢ ɨɫɧɨɜɧɵɯ ɮɨɪɦɭɥ, ɨɩɢɫɵɜɚɸɳɢɯ ɹɜɥɟɧɢɹ ɢɥɢ ɩɪɨɰɟɫɫɵ, ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɟ
ɞɚɧɧɨɦɭ ɪɚɡɞɟɥɭ, ɱɬɨ ɩɨɦɨɝɚɟɬ ɫɬɭɞɟɧɬɭ ɫɢɫɬɟɦɚɬɢɡɢɪɨɜɚɬɶ ɬɟɨɪɟɬɢɱɟɫɤɢɟ ɡɧɚɧɢɹ ɢ
ɭɦɟɧɶɲɚɟɬ ɡɚɬɪɚɬɵ ɜɪɟɦɟɧɢ ɧɚ ɪɟɲɟɧɢɟ ɡɚɞɚɱ. ɉɨɞɨɛɪɚɧɧɵɟ ɢ ɫɨɫɬɚɜɥɟɧɧɵɟ ɜ ɫɛɨɪɧɢɤɟ
ɡɚɞɚɱɢ ɫɜɹɡɚɧɵ ɫ ɩɪɨɰɟɫɫɚɦɢ, ɩɪɨɬɟɤɚɸɳɢɦɢ ɜ ɯɨɥɨɞɢɥɶɧɨɣ ɬɟɯɧɢɤɟ, ɧɚɝɪɟɜɚɬɟɥɶɧɵɯ
ɩɪɢɛɨɪɚɯ, ɚ ɬɚɤɠɟ ɫ ɩɪɨɰɟɫɫɚɦɢ ɜɟɧɬɢɥɹɰɢɢ, ɢ ɤɨɧɞɢɰɢɨɧɢɪɨɜɚɧɢɹ ɩɨɦɟɳɟɧɢɣ. ɉɪɢ ɷɬɨɦ
ɡɚɞɚɱɢ ɫɢɫɬɟɦɚɬɢɡɢɪɨɜɚɧɵ ɩɨ ɪɚɡɞɟɥɚɦ ɩɪɨɝɪɚɦɦɵ. ɂɫɩɨɥɶɡɨɜɚɧɧɚɹ ɜ ɦɟɬɨɞɢɱɟɫɤɨɦ
ɩɨɫɨɛɢɢ ɬɟɪɦɢɧɨɥɨɝɢɹ, ɨɛɨɡɧɚɱɟɧɢɹ ɢ ɟɞɢɧɢɰɵ ɮɢɡɢɱɟɫɤɢɯ ɜɟɥɢɱɢɧ ɫɨɨɬɜɟɬɫɬɜɭɸɬ
ɫɬɚɧɞɚɪɬɚɦ ɩɨ ɛɚɡɨɜɵɦ ɞɥɹ ɬɟɨɪɟɬɢɱɟɫɤɢɯ ɩɪɨɰɟɫɫɨɜ ȻɆɉ ɧɚɭɤɚɦ: ɮɢɡɢɤɟ, ɬɟɯɧɢɱɟɫɤɨɣ
ɬɟɪɦɨɞɢɧɚɦɢɤɟ ɢ ɬɟɩɥɨɩɟɪɟɞɚɱɟ.
Ɋɟɲɟɧɢɟ ɧɟɤɨɬɨɪɵɯ ɡɚɞɚɱ ɞɨɥɠɧɨ ɜɵɩɨɥɧɹɬɶɫɹ ɝɪɚɮɢɱɟɫɤɢɦɢ ɦɟɬɨɞɚɦɢ ɩɪɢ ɩɨɦɨɳɢ
ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɢɯ ɞɢɚɝɪɚɦɦ, ɩɪɟɞɫɬɚɜɥɟɧɧɵɯ ɜ ɩɪɢɥɨɠɟɧɢɢ ɩɨɫɨɛɢɹ.
ɉɟɪɟɞ ɪɟɲɟɧɢɟɦ ɡɚɞɚɱɢ ɧɟɨɛɯɨɞɢɦɨ ɤɪɚɬɤɨ ɡɚɩɢɫɚɬɶ ɟɟ ɭɫɥɨɜɢɟ. Ɋɟɲɟɧɢɟ ɫɥɟɞɭɟɬ
ɩɪɨɜɨɞɢɬɶ ɜ ɨɛɳɟɦ ɜɢɞɟ, ɱɬɨ, ɤɚɤ ɩɪɚɜɢɥɨ, ɭɩɪɨɳɚɟɬ ɩɨɫɥɟɞɭɸɳɢɟ ɜɵɱɢɫɥɟɧɢɹ.
ɉɨɞɫɬɚɜɥɹɬɶ ɱɢɫɥɟɧɧɵɟ ɡɧɚɱɟɧɢɹ ɜɟɥɢɱɢɧ Ɍȼ ɨɤɨɧɱɚɬɟɥɶɧɵɟ ɮɨɪɦɭɥɵ ɧɭɠɧɨ,
ɩɪɟɞɜɚɪɢɬɟɥɶɧɨ ɩɟɪɟɜɟɞɹ ɢɯ ɜ ɫɢɫɬɟɦɭ ɋɂ, ɟɫɥɢ ɜ ɭɫɥɨɜɢɢ ɡɚɞɚɱɢ ɨɧɢ ɡɚɩɢɫɚɧɵ ɜ ɞɪɭɝɨɣ
ɫɢɫɬɟɦɟ. ɉɪɢ ɩɨɞɫɬɚɧɨɜɤɟ ɱɢɫɟɥ ɧɟɨɛɯɨɞɢɦɨ ɫɨɯɪɚɧɹɬɶ ɞɜɟ ɡɧɚɱɚɳɢɟ ɰɢɮɪɵ ɩɨɫɥɟ
ɡɚɩɹɬɨɣ, ɭɱɢɬɵɜɚɹ ɩɨɪɹɞɨɤ ɱɢɫɥɚ. ȼ ɬɚɤɨɦ ɠɟ ɜɢɞɟ ɫɥɟɞɭɟɬ ɡɚɩɢɫɵɜɚɬɶ ɨɬɜɟɬ, ɨɛɹɡɚɬɟɥɶɧɨ
ɭɤɚɡɚɜ ɟɞɢɧɢɰɭ ɢɡɦɟɪɟɧɢɹ. ɇɚɩɪɢɦɟɪ: Q
o
= 1,24 ɤȼɬ, Į = 3,05·10
4
ȼɬ/(ɦ
2
Ʉ). ȿɞɢɧɢɰɚ
ɢɡɦɟɪɟɧɢɹ ɜ ɨɬɜɟɬɟ ɨɬɫɭɬɫɬɜɭɟɬ, ɟɫɥɢ ɢɦ ɹɜɥɹɟɬɫɹ ɱɢɫɥɨ ɩɨɞɨɛɢɹ ɢɥɢ ɩɨɤɚɡɚɬɟɥɶ
ɚɞɢɚɛɚɬɵ, ɢɥɢ ɨɧ ɩɨɥɭɱɟɧ ɜ ɛɟɡɪɚɡɦɟɪɧɵɯ ɩɟɪɟɦɟɧɧɵɯ.

2.1. ɉɚɪɚɦɟɬɪɵ ɫɨɫɬɨɹɧɢɹ. ɍɪɚɜɧɟɧɢɹ ɫɨɫɬɨɹɧɢɹ.
Ɉɫɧɨɜɧɵɟ ɮɨɪɦɭɥɵ.
Ⱥɛɫɨɥɸɬɧɨɟ ɞɚɜɥɟɧɢɟ ɝɚɡɚ:
S
n
F
P
ɝɞɟ
n
F - ɧɨɪɦɚɥɶɧɚɹ ɫɨɫɬɚɜɥɹɸɳɚɹ ɫɢɥɵ;
S - ɩɥɨɳɚɞɶ ɩɨɜɟɪɯɧɨɫɬɢ, ɧɚ ɤɨɬɨɪɭɸ ɞɟɣɫɬɜɭɟɬ ɫɢɥɚ.
15.273 CtTK
$
- ɚɛɫɨɥɸɬɧɚɹ ɬɟɦɩɟɪɚɬɭɪɚ.
ɍɞɟɥɶɧɵɣ ɨɛɴɟɦ ɢ ɩɥɨɬɧɨɫɬɶ ɝɚɡɚ:
m
V
X
,
V
m
ȡ
ɝɞɟ V - ɨɛɴɟɦ ɝɚɡɚ; m - ɦɚɫɫɚ ɝɚɡɚ.
ɍɪɚɜɧɟɧɢɟ ɫɨɫɬɨɹɧɢɹ ɢɞɟɚɥɶɧɨɝɨ ɝɚɡɚ:
RTP
X
ɝɞɟ
P
P
R
R
- ɭɞɟɥɶɧɚɹ ɝɚɡɨɜɚɹ ɩɨɫɬɨɹɧɧɚɹ;
P
R - ɭɧɢɜɟɪɫɚɥɶɧɚɹ ɝɚɡɨɜɚɹ ɩɨɫɬɨɹɧɧɚɹ;
P
- ɦɨɥɹɪɧɚɹ ɦɚɫɫɚ ɝɚɡɚ.
Ɂɚɞɚɱɢ.
1. ȼɨ ɫɤɨɥɶɤɨ ɪɚɡ ɢɡɦɟɧɢɬɶɫɹ ɩɥɨɬɧɨɫɬɶ ɝɚɡɚ ɜ ɫɨɫɭɞɟ, ɟɫɥɢ ɩɪɢ ɩɨɫɬɨɹɧɧɨɣ ɬɟɦɩɟɪɚɬɭɪɟ
ɩɨɤɚɡɚɧɢɟ ɦɚɧɨɦɟɬɪɚ ɭɜɟɥɢɱɢɬɶɫɹ ɨɬ 0.3 Ɇɉɚ ɞɨ 1.9 Ɇɉɚ ?
Ȼɚɪɨɦɟɬɪɢɱɟɫɤɨɟ ɞɚɜɥɟɧɢɟ ɩɪɢɧɹɬɶ ɪɚɜɧɵɦ 0.1 Ɇɉɚ
12
5
U
U
2. ȼ ɫɨɫɭɞɟ ɩɪɢ ɬɟɦɩɟɪɚɬɭɪɟ ɋ
$
20 ɧɚɯɨɞɢɬɶɫɹ ɜɨɡɞɭɯ. ɉɨɤɚɡɚɧɢɹ ɜɚɤɭɭɦɦɟɬɪɚ
ɫɨɫɬɚɜɥɹɸɬ 10ɤɉɚ, ɩɨɤɚɡɚɧɢɹ ɛɚɪɨɦɟɬɪɚ 100ɤɉɚ. Ʉɚɤɨɜɚ ɩɥɨɬɧɨɫɬɶ ɜɨɡɞɭɯɚ ɩɪɢ ɷɬɢɯ
ɭɫɥɨɜɢɹɯ?
3. Ɉɩɪɟɞɟɥɢɬɶ ɭɞɟɥɶɧɵɣ ɨɛɴɟɦ ɢ ɩɥɨɬɧɨɫɬɶ ɜɨɞɹɧɨɝɨ ɩɚɪɚ ɩɪɢ ɧɨɪɦɚɥɶɧɵɯ ɭɫɥɨɜɢɹɯ,
ɫɱɢɬɚɹ ɟɝɨ ɢɞɟɚɥɶɧɵɦ ɝɚɡɨɦ.
4. ɉɨ ɬɪɭɛɨɩɪɨɜɨɞɭ ɩɪɨɬɟɤɚɟɬ 0.12 ɦ
3
/ɫ ɯɥɚɞɚɝɟɧɬɚ ɩɪɢ ɬɟɦɩɟɪɚɬɭɪɟ
ɋ
$
37
ɢ ɞɚɜɥɟɧɢɟɦ
P=1Ɇɉɚ. Ɉɩɪɟɞɟɥɢɬɶ ɦɚɫɫɨɜɵɣ ɪɚɫɯɨɞ ɯɥɚɞɚɝɟɧɬɚ, ɩɨɥɚɝɚɹ ɟɝɨ ɩɪɢ ɷɬɢɯ ɭɫɥɨɜɢɹɯ
ɢɞɟɚɥɶɧɵɦ ɝɚɡɨɦ. ɉɪɢɧɹɬɶ ɟɝɨ ɭɞɟɥɶɧɭɸ ɝɚɡɨɜɭɸ ɩɨɫɬɨɹɧɧɭɸ
Ʉɤɝ
Ⱦɠ
R
97 .

2.2. ȼɧɭɬɪɟɧɧɹɹ ɷɧɟɪɝɢɹ. ɗɧɬɚɥɶɩɢɹ. ɗɧɬɪɨɩɢɹ.
Ɉɫɧɨɜɧɵɟ ɮɨɪɦɭɥɵ.
ȼɧɭɬɪɟɧɧɹɹ ɷɧɟɪɝɢɹ ɢɞɟɚɥɶɧɨɝɨ ɝɚɡɚ:
2
TiR
U
P
Q
ɝɞɟ
Q
- ɱɢɫɥɨ ɦɨɥɟɣ; i - ɱɢɫɥɨ ɫɬɟɩɟɧɟɣ ɫɜɨɛɨɞɵ ɦɨɥɟɤɭɥɵ.
ɉɨɥɧɚɹ ɷɧɟɪɝɢɹ ɫɢɫɬɟɦɵ:
ɜɧ
EUE
ɝɞɟ
ɜɧ
E - ɜɧɟɲɧɹɹ ɷɧɟɪɝɢɹ, ɫɜɹɡɚɧɧɚɹ ɫ ɞɜɢɠɟɧɢɟɦ ɫɢɫɬɟɦɵ ɤɚɤ ɰɟɥɨɝɨ ɢ ɩɨɥɨɠɟɧɢɟ ɟɟ ɜ
ɩɨɥɟ ɫɢɥ.
ɂɡɦɟɧɟɧɢɟ ɜɧɭɬɪɟɧɧɟɣ ɷɧɟɪɝɢɢ ɜ ɡɚɦɤɧɭɬɨɦ (ɤɪɭɝɨɜɨɦ) ɩɪɨɰɟɫɫɟ:
³
' 0
0
duU
ɗɧɬɚɥɶɩɢɹ ɢɞɟɚɥɶɧɨɝɨ ɝɚɡɚ:
hU P U RT
X
Ⱦɢɮɮɟɪɟɧɰɢɚɥ ɷɧɬɪɨɩɢɢ:
T
dQ
ds
ɝɞɟ dQ – ɛɟɫɤɨɧɟɱɧɨ ɦɚɥɨɟ ɤɨɥɢɱɟɫɬɜɨ ɬɟɩɥɨɬɵ ɜ ɷɥɟɦɟɧɬɚɪɧɨɦ ɨɛɪɚɬɢɦɨɦ ɩɪɨɰɟɫɫɟ.
ɂɡɦɟɧɟɧɢɟ ɷɧɬɪɨɩɢɢ ɜ ɤɨɧɟɱɧɨɦ ɨɛɪɚɬɢɦɨɦ ɩɪɨɰɟɫɫɟ:
³
'
2
1
12
T
dq
SSS
ɝɞɟ
m
dQ
dq
Ɂɚɞɚɱɢ.
5. Ɉɩɪɟɞɟɥɢɬɶ ɢɡɦɟɧɟɧɢɟ ɭɞɟɥɶɧɨɣ ɷɧɬɚɥɶɩɢɢ ɜɨɡɞɭɯɚ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɟɝɨ ɬɟɦɩɟɪɚɬɭɪɵ ɨɬ
Ct
$
20
1
ɞɨ Ct
$
100
2
. 28.9
ɪ
Ⱦɠ
ɋ
ɤɦɨɥɶ Ʉ
P
§·
¨¸
©¹
6. ȼ ɤɨɦɩɪɟɫɫɨɪɟ ɯɨɥɨɞɢɥɶɧɨɣ ɭɫɬɚɧɨɜɤɢ ɫɠɢɦɚɟɬɫɹ ɯɥɚɞɚɝɟɧɬ (µ= 90 ɝ/ɦɨɥɶ). ȿɝɨ
ɧɚɱɚɥɶɧɚɹ ɬɟɦɩɟɪɚɬɭɪɚ Ct
$
20
1
, ɬɟɦɩɟɪɚɬɭɪɚ ɩɨɫɥɟ ɫɠɚɬɢɹ Ct
$
60
2
. Ɉɩɪɟɞɟɥɢɬɶ
ɢɡɦɟɧɟɧɢɟ ɜɧɭɬɪɟɧɧɟɣ ɷɧɟɪɝɢɢ ɢ ɷɧɬɚɥɶɩɢɢ ɯɥɚɞɚɝɟɧɬɚ ɜ ɩɪɨɰɟɫɫɟ ɫɠɚɬɢɹ.
7. Ɉɩɪɟɞɟɥɢɬɶ ɢɡɦɟɧɟɧɢɟ ɷɧɬɪɨɩɢɢ 1 ɥɢɬɪɚ ɜɨɞɵ. ȿɫɥɢ ɩɪɢ ɬɟɦɩɟɪɚɬɭɪɟ ɋ
$
80 ɢɫɩɚɪɢɥɨɫɶ
5% ɨɬ ɷɬɨɝɨ ɤɨɥɢɱɟɫɬɜɚ. Ɍɟɩɥɨɬɚ ɩɚɪɨɨɛɪɚɡɨɜɚɧɢɹ 2309 ɤȾɠ/ɤɝ

8. ȼ ɜɨɡɞɭɯɟ ɨɛɴɟɦɨɦ 300ɥ ɩɪɢ ɬɟɦɩɟɪɚɬɭɪɟ ɋ
$
28 ɩɨɞɦɟɲɢɜɚɟɬɫɹ 60ɥ ɜɨɡɞɭɯɚ ɩɪɢ
ɬɟɦɩɟɪɚɬɭɪɟ ɋ
$
14 . Ɉɩɪɟɞɟɥɢɬɶ ɨɛɳɟɟ ɢɡɦɟɧɟɧɢɟ ɷɧɬɪɨɩɢɢ ɜɨɡɞɭɯɚ ɜ ɪɟɡɭɥɶɬɚɬɟ ɷɬɨɝɨ
ɩɪɨɰɟɫɫɚ ɫɦɟɲɟɧɢɹ. Ɍɟɩɥɨɟɦɤɨɫɬɶ ɜɨɡɞɭɯɚ
29 ( )
ɪ
ɋɤȾɠɤɦɨɥɶɄ
P
.
2.3. Ɋɚɛɨɬɚ. Ɍɟɩɥɨɬɚ. Ɍɟɩɥɨɟɦɤɨɫɬɶ.
Ɉɫɧɨɜɧɵɟ ɮɨɪɦɭɥɵ.
Ⱥɧɚɥɢɬɢɱɟɫɤɨɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɷɥɟɦɟɧɬɚɪɧɨɣ ɪɚɛɨɬɵ:
dl Pd
X
Ⱥɧɚɥɢɬɢɱɟɫɤɨɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɪɚɛɨɬɵ ɜ ɤɨɧɟɱɧɨɦ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɨɦ ɩɪɨɰɟɫɫɟ:
2
1
()lPd
X
X
XX
³
Ⱥɧɚɥɢɬɢɱɟɫɤɨɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɷɥɟɦɟɧɬɚɪɧɨɝɨ ɤɨɥɢɱɟɫɬɜɚ ɬɟɩɥɨɬɵ:
Tdsdq
Ⱥɧɚɥɢɬɢɱɟɫɤɨɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɤɨɥɢɱɟɫɬɜɚ ɬɟɩɥɨɬɵ ɜ ɤɨɧɟɱɧɨɦ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɨɦ
ɩɪɨɰɟɫɫɟ:
³
2
1
)(
S
S
dSSTq
ɂɫɬɢɧɧɚɹ ɬɟɩɥɨɟɦɤɨɫɬɶ ɜ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɨɦ ɩɪɨɰɟɫɫɟ X:
dT
dq
C
x
x
ɋɪɟɞɧɹɹ ɬɟɩɥɨɟɦɤɨɫɬɶ ɜ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɨɦ ɩɪɨɰɟɫɫɟ X ɜ ɢɧɬɟɪɜɚɥɟ ɬɟɦɩɟɪɚɬɭɪ (t
1
,t
2
):
12
2
1
tt
q
ɋ
x
t
t
xm
ɋɜɹɡɶ ɦɟɠɞɭ ɭɞɟɥɶɧɵɦɢ ɬɟɩɥɨɟɦɤɨɫɬɹɦɢ:
X
P
P
x
x
x
C
C
C
c
ɝɞɟ
x
C - ɭɞɟɥɶɧɚɹ ɦɚɫɫɨɜɚɹ ɬɟɩɥɨɟɦɤɨɫɬɶ;
x
C
P
- ɭɞɟɥɶɧɚɹ ɦɨɥɶɧɚɹ ɬɟɩɥɨɟɦɤɨɫɬɶ;
x
C
c
- ɭɞɟɥɶɧɚɹ ɨɛɴɟɦɧɚɹ ɬɟɩɥɨɟɦɤɨɫɬɶ.
ɍɪɚɜɧɟɧɢɟ Ɇɚɣɟɪɚ:
RCC
p
X
ɉɨɤɚɡɚɬɟɥɶ ɚɞɢɚɛɚɬɵ:

K
C
C
p
X
ȼɵɱɢɫɥɟɧɢɟ ɤɨɥɢɱɟɫɬɜɚ ɬɟɩɥɨɬɵ ɩɨ ɢɡɜɟɫɬɧɨɣ ɢɫɬɢɧɨɣ ɬɟɩɥɨɟɦɤɨɫɬɢ:
dtCdq
xx
,
³
2
1
)(
t
t
xx
dttCq
ȼɵɱɢɫɥɟɧɢɟ ɤɨɥɢɱɟɫɬɜɚ ɬɟɩɥɨɬɵ ɩɪɢ ɢɡɜɟɫɬɧɨɣ ɫɪɟɞɧɟɣ ɬɟɩɥɨɟɦɤɨɫɬɢ:
1
0
2
0
12
tCtCq
t
xm
t
xmx
Ɂɚɞɚɱɢ.
9. Ɉɩɪɟɞɟɥɢɬɶ ɤɨɥɢɱɟɫɬɜɨ ɬɟɩɥɨɬɵ ɧɟɨɛɯɨɞɢɦɨɟ ɞɥɹ ɧɚɝɪɟɜɚɧɢɹ 4ɦ
3
ɞɜɭɯɚɬɨɦɧɨɝɨ ɝɚɡɚ ɧɚ ɋ
$
100 ɩɪɢ ɩɨɫɬɨɹɧɧɨɦ ɨɛɴɟɦɟ, ɟɫɥɢ ɞɨ ɧɚɝɪɟɜɚɧɢɹ ɨɧ ɧɚɯɨɞɢɥɫɹ ɩɪɢ
ɧɨɪɦɚɥɶɧɵɯ ɭɫɥɨɜɢɹɯ.
10. Ɉɩɪɟɞɟɥɢɬɶ ɡɧɚɱɟɧɢɟ ɭɞɟɥɶɧɨɣ ɦɚɫɫɨɜɨɣ ɬɟɩɥɨɟɦɤɨɫɬɢ ɩɪɢ ɩɨɫɬɨɹɧɧɨ ɨɛɴɟɦɟɢ
ɩɨɫɬɨɹɧɧɨɦ ɞɚɜɥɟɧɢɢ.
11. Ɉɩɪɟɞɟɥɢɬɶ ɫɪɟɞɧɸɸ ɦɚɫɫɨɜɭɸ ɬɟɩɥɨɟɦɤɨɫɬɶ ɩɪɢ ɩɨɫɬɨɹɧɧɨɦ ɨɛɴɟɦɟ ɞɥɹ ɋɈ
2
ɜ
ɬɟɦɩɟɪɚɬɭɪɧɨɦ ɢɧɬɟɪɜɚɥɟ
ɋ
$
7020 , ɟɫɥɢ ɢɡɜɟɫɬɧɨ, ɱɬɨ ɟɝɨ ɢɫɬɢɧɧɚɹ ɦɨɥɶɧɚɹ ɬɟɩɥɨɟɦɤɨɫɬɶ
tɋ
ɪ
022.086.35
P
12. Ƚɚɡ ɧɚɯɨɞɹɳɢɣɫɹ ɜ ɫɨɫɬɨɹɧɢɢ 1
)2.0(
1
ɆɉɚP ɩɟɪɟɜɨɞɢɬɶɫɹ ɜ ɫɨɫɬɨɹɧɢɟ 2
)6.0(
2
ɆɉɚP ɞɜɨɹɤɢɦ ɨɛɪɚɡɨɦ: 1) ɜ ɩɪɨɰɟɫɫɟ 1ɚ2 ɫɧɚɱɚɥɚ ɜɵɩɨɥɧɹɟɬɫɹ ɩɨɞɜɨɞ ɬɟɩɥɨɬɵ ɩɪɢ
const
X
; 2) ɜ ɩɪɨɰɟɫɫɟ 1ɜ2 ɫɧɚɱɚɥɚ ɩɪɨɜɨɞɢɬɫɹ ɪɚɫɲɢɪɟɧɢɟ ɩɪɢ Ɋ=const, ɚ ɡɚɬɟɦ ɩɨɞɜɨɞ
ɬɟɩɥɨɬɵ ɩɪɢ
const
X
. ɂɡɦɟɧɟɧɢɟ ɨɛɴɟɦɚ ɫɨɫɬɚɜɥɹɟɬ V
2
-V
1
=0.4ɦ
3
ɂɡɨɛɪɚɡɢɬɶ ɜɟɥɢɱɢɧɵ ɪɚɛɨɬ ɜ ɩɪɨɰɟɫɫɚɯ 1ɚ2 ɢ 1ɜ2. Ɉɩɪɟɞɟɥɢɬɶ, ɛɭɞɭɬ ɥɢ ɨɬɥɢɱɚɬɶɫɹ ɜ ɷɬɢɯ
ɩɪɨɰɟɫɫɚɯ ɤɨɥɢɱɟɫɬɜɚ ɩɨɞɜɟɞɟɧɧɨɣ ɢ ɨɬɜɟɞɟɧɧɨɣ ɬɟɩɥɨɬɵ, ɢ ɟɫɥɢ ɞɚ, ɬɨ ɧɚɫɤɨɥɶɤɨ.
2.4. ɉɟɪɜɵɣ ɡɚɤɨɧ ɬɟɪɦɨɞɢɧɚɦɢɤɢ.
Ɉɫɧɨɜɧɵɟ ɮɨɪɦɭɥɵ.
ɍɪɚɜɧɟɧɢɟ ɩɟɪɜɨɝɨ ɡɚɤɨɧɚ ɬɟɪɦɨɞɢɧɚɦɢɤɢ ɞɥɹ ɷɥɟɦɟɧɬɚɪɧɨɝɨ ɩɪɨɰɟɫɫɚ:
dldudq
ɍɪɚɜɧɟɧɢɟ ɩɟɪɜɨɝɨ ɡɚɤɨɧɚ ɬɟɪɦɨɞɢɧɚɦɢɤɢ ɞɥɹ ɤɨɧɟɱɧɨɝɨ ɩɪɨɰɟɫɫɚ:
lUq '
ɍɪɚɜɧɟɧɢɟ ɩɟɪɜɨɝɨ ɡɚɤɨɧɚ ɬɟɪɦɨɞɢɧɚɦɢɤɢ ɞɥɹ ɤɪɭɝɨɜɨɝɨ ɩɪɨɰɟɫɫɚ:
³³
dldq
Ɍɟɪɦɨɞɢɧɚɦɢɱɟɫɤɨɟ ɬɨɠɞɟɫɬɜɨ:
dpdhpdduTds
X
X

Ɂɚɞɚɱɢ.
13. ɂɞɟɚɥɶɧɵɣ ɞɜɭɯɚɬɨɦɧɵɣ ɝɚɡ ɩɥɨɬɧɨɫɬɶɸ
3
/10 ɦɤɝ
U
, ɧɚɯɨɞɹɳɢɣɫɹ ɩɨɞ ɞɚɜɥɟɧɢɟɦ
ɆɉɚP 8,0
1
ɪɚɫɲɢɪɹɟɬɫɹ ɩɨ ɡɚɤɨɧɭ constPV
K
4,1 k ɞɨ ɭɞɟɥɶɧɨɝɨ ɨɛɴɟɦɚ
ɤɝɦV /25,0
3
2
. ȿɝɨ ɞɚɜɥɟɧɢɟ ɩɪɢ ɷɬɨɦ ɫɬɚɧɨɜɢɬɫɹ ɆɉɚP 3,0
2
. Ɉɩɪɟɞɟɥɢɬɶ ɪɚɛɨɬɭ
ɪɚɫɲɢɪɟɧɢɹ. Ʉɚɤɨɜɨ ɢɡɦɟɧɟɧɢɟ ɜɧɭɬɪɟɧɧɟɣ ɷɧɟɪɝɢɢ ɝɚɡɚ ɜ ɷɬɨɦ ɩɪɨɰɟɫɫɟ?
14. Ⱥɡɨɬ ɦɚɫɫɨɣ
ɤɝm 6 ɩɪɢ ɩɨɫɬɨɹɧɧɨɦ ɨɛɴɟɦɟ ɧɚɝɪɟɥɢ ɧɚ ɜɟɥɢɱɢɧɭ Ct
$
100 ' .
Ɉɩɪɟɞɟɥɢɬɶ: 1) ɤɨɥɢɱɟɫɬɜɨ ɬɟɩɥɨɬɵ, ɫɨɨɛɳɟɧɧɨɣ ɝɚɡɭ; 2) ɢɡɦɟɧɟɧɢɟ ɜɧɭɬɪɟɧɧɟɣ ɷɧɟɪɝɢɢ; 3)
ɫɨɜɟɪɲɟɧɧɭɸ ɝɚɡɨɦ ɪɚɛɨɬɭ.
15. ȼ ɪɟɡɭɥɶɬɚɬɟ ɨɯɥɚɠɞɟɧɢɹ ɜ ɤɨɧɞɟɧɫɚɬɨɪɟ ɯɨɥɨɞɢɥɶɧɨɝɨ ɚɝɟɧɬɚ ɫɠɚɬɨɝɨ ɤɨɦɩɪɟɫɫɨɪɨɦ ɞɨ
ɞɚɜɥɟɧɢɹ
ɆɉɚP 0,1 , ɞɨ ɫɨɫɬɨɹɧɢɹ ɫɭɯɨɝɨ ɧɚɫɵɳɟɧɧɨɝɨ ɩɚɪɚ, ɟɝɨ ɭɞɟɥɶɧɵɣ ɨɛɴɟɦ
ɭɦɟɧɶɲɢɥɫɹ ɨɬ
ɤɝɦ /022,0
3
ɞɨ ɤɝɦ /018,0
3
, ɚ ɷɧɬɚɥɶɩɢɹ ɨɬ
ɤɝ
ɤȾɠ
590 ɞɨ
ɤɝ
ɤȾɠ
570 .
Ɉɩɪɟɞɟɥɢɬɶ ɤɨɥɢɱɟɫɬɜɨ ɨɬɜɟɞɟɧɧɨɣ ɬɟɩɥɨɬɵ ɢ ɢɡɦɟɧɟɧɢɟ ɜɧɭɬɪɟɧɧɟɣ ɷɧɟɪɝɢɢ ɯɥɚɞɚɝɟɧɬɚ.
16.Ʉɨɦɩɪɟɫɫɨɪɨ ɫɠɢɦɚɟɬ ɚɞɢɚɛɚɬɧɨ
ɱɤɝ /18 ɮɪɟɨɧɚ. ɉɪɢ ɷɬɨɦ ɟɝɨ ɷɧɬɚɥɶɩɢɹ ɭɜɟɥɢɱɢɜɚɟɬɫɹ
ɧɚ
ɤɝɤȾɠ /20
. Ɉɩɪɟɞɟɥɢɬɶ ɦɨɳɧɨɫɬɶ ɩɪɢɜɨɞɚ ɤɨɦɩɪɟɫɫɨɪɚ.
2.5. Ɉɫɧɨɜɧɵɟ ɬɟɪɦɨɞɢɧɚɦɢɱɟɫɤɢɟ ɩɪɨɰɟɫɫɵ ɢɞɟɚɥɶɧɵɯ ɝɚɡɨɜ.
Ɉɫɧɨɜɧɵɟ ɮɨɪɦɭɥɵ.
1) ɂɡɨɯɨɪɧɵɣ ɩɪɨɰɟɫɫ:
0
X
d
, const
X
Ɂɚɜɢɫɢɦɨɫɬɶ ɦɟɠɞɭ P ɢ T :
const
T
P
Ɍɟɪɦɨɞɢɧɚɦɢɱɟɫɤɚɹ ɪɚɛɨɬɚ:
0
X
l
ɂɡɦɟɧɟɧɢɟ ɷɧɬɪɨɩɢɢ:
1
2
ln
T
T
CS
m
XX
'
ɉɟɪɜɵɣ ɡɚɤɨɧ ɬɟɪɦɨɞɢɧɚɦɢɤɢ:
Uq '
X
2) ɂɡɨɛɚɪɧɵɣ ɩɪɨɰɟɫɫ:
0 dP , constP
Ɂɚɜɢɫɢɦɨɫɬɶ ɦɟɠɞɭ
X
ɢ
T
:
const
T
X
Ɍɟɪɦɨɞɢɧɚɦɢɱɟɫɤɚɹ ɪɚɛɨɬɚ:
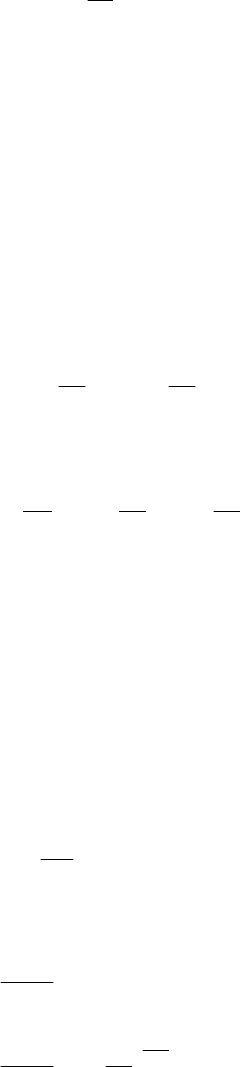
)()(
1212
TTRPl
p
X
X
ɂɡɦɟɧɟɧɢɟ ɷɧɬɪɨɩɢɢ:
1
2
ln
T
T
CS
pmp
'
ɉɟɪɜɵɣ ɡɚɤɨɧ ɬɟɪɦɨɞɢɧɚɦɢɤɢ:
lUq
p
' , hq
p
'
3) ɂɡɨɬɟɪɦɢɱɟɫɤɢɣ ɩɪɨɰɟɫɫ:
0 dt
,
constT
Ɂɚɜɢɫɢɦɨɫɬɶ ɦɟɠɞɭ
P
ɢ
X
:
constP
X
Ɍɟɪɦɨɞɢɧɚɦɢɱɟɫɤɚɹ ɪɚɛɨɬɚ:
2
1
1
2
lnln
P
P
RTRTl
T
X
X
ɂɡɦɟɧɟɧɢɟ ɷɧɬɪɨɩɢɢ:
2
1
1
2
lnln
P
P
RR
T
q
S
T
T
'
X
X
ɉɟɪɜɵɣ ɡɚɤɨɧ ɬɟɪɦɨɞɢɧɚɦɢɤɢ:
TT
lq
4) Ⱥɞɢɚɛɚɬɧɵɣ ɩɪɨɰɟɫɫ:
0
dq
Ɂɚɜɢɫɢɦɨɫɬɶ ɦɟɠɞɭ
P
ɢ
X
:
constP
K
X
ɝɞɟ
X
C
C
K
P
- ɩɨɤɚɡɚɬɟɥɶ ɚɞɢɚɛɚɬɵ.
Ɍɟɪɦɨɞɢɧɚɦɢɱɟɫɤɚɹ ɪɚɛɨɬɚ:
)(
1
1
2211
XX
PP
K
l
q
»
¼
º
«
¬
ª
R
K
q
P
P
K
RT
l
1
1
21
)(1
1
ɂɡɦɟɧɟɧɢɟ ɷɧɬɪɨɩɢɢ:
0 dS , constS
ɉɟɪɜɵɣ ɡɚɤɨɧ ɬɟɪɦɨɞɢɧɚɦɢɤɢ:
Ul
q
'
5) ɉɨɥɢɬɪɨɩɧɵɣ ɩɪɨɰɟɫɫ:

constC
n
,
X
CC
CC
n
n
Pn
- ɩɨɤɚɡɚɬɟɥɶ ɩɨɥɢɬɪɨɩɵ.
Ɂɚɜɢɫɢɦɨɫɬɶ ɦɟɠɞɭ
P
ɢ
X
:
contsP
n
X
Ɍɟɪɦɨɞɢɧɚɦɢɱɟɫɤɚɹ ɪɚɛɨɬɚ:
)(
1
1
2211
XX
PP
n
l
n
»
¼
º
«
¬
ª
n
n
n
P
P
n
RT
l
1
1
21
)(1
1
ɂɡɦɟɧɟɧɢɟ ɷɧɬɪɨɩɢɢ:
1
2
ln
T
T
CS
nmn
'
ɉɟɪɜɵɣ ɡɚɤɨɧ ɬɟɪɦɨɞɢɧɚɦɢɤɢ:
lUq
n
'
Ɂɚɞɚɱɢ.
17. Ɉɬ ɜɨɡɞɭɯɚ ɦɚɫɫɨɣ
ɤɝ70 ɩɪɢ ɩɨɫɬɨɹɧɧɨɦ ɨɛɴɟɦɟ ɨɬɜɨɞɢɬɫɹ ɆȾɠ14 ɬɟɩɥɨɬɵ, ɩɪɢ ɷɬɨɦ
ɞɚɜɥɟɧɢɟ ɜɨɡɞɭɯɚ ɭɦɟɧɶɲɢɬɫɹ ɜ ɞɜɚ ɪɚɡɚ. Ɉɩɪɟɞɟɥɢɬɶ ɬɟɦɩɟɪɚɬɭɪɭ ɜɨɡɞɭɯɚ ɩɨɫɥɟ
ɨɯɥɚɠɞɟɧɢɹ, ɩɪɢɧɹɜ
ɄɤɝɤȾɠC
V
/718,0.
18. ȼ ɭɫɬɚɧɨɜɤɟ ɜɨɡɞɭɲɧɨɝɨ ɨɬɨɩɥɟɧɢɹ ɧɚɪɭɠɧɵɣ ɜɨɡɞɭɯ ɩɪɢ Ct
$
10
1
ɧɚɝɪɟɜɚɟɬɫɹ ɜ
ɤɚɥɨɪɢɮɟɪɟ ɩɪɢ ɩɨɫɬɨɹɧɧɨɦ ɞɚɜɥɟɧɢɢ ɆɉɚP 1,0 ɞɨ
ɋ
$
50 . Ʉɚɤɨɟ ɤɨɥɢɱɟɫɬɜɨ ɬɟɩɥɨɬɵ ɧɚɞɨ
ɡɚɬɪɚɬɢɬɶ ɞɥɹ ɧɚɝɪɟɜɚ
3
300ɦ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ?
19. Ɉɩɪɟɞɟɥɢɬɶ, ɤɚɤɚɹ ɱɚɫɬɶ ɬɟɩɥɨɬɵ, ɩɨɞɜɨɞɢɦɨɣ ɤ ɜɨɡɞɭɯɭ ɜ ɢɡɨɛɚɪɧɨɦ ɩɪɨɰɟɫɫɟ,
ɪɚɫɯɨɞɭɟɬɫɹ ɧɚ ɪɚɛɨɬɭ, ɚ ɤɚɤɚɹ ɧɚ ɢɡɦɟɧɟɧɢɟ ɜɧɭɬɪɟɧɧɟɣ ɷɧɟɪɝɢɢ.
20. ȼɨɡɞɭɯ ɨɛɴɟɦɨɦ
3
1,0 ɦV ɩɪɢ ɞɚɜɥɟɧɢɢ ɆɉɚP 1
1
ɢ ɬɟɦɩɟɪɚɬɭɪɟ Ct
$
24
1
ɪɚɫɲɢɪɹɟɬɫɹ ɜ ɰɢɥɢɧɞɪɟ ɫ ɩɨɞɜɢɠɧɵɦ ɩɨɪɲɧɟɦ ɞɨ
Ɇɉɚ1,0
. Ɉɩɪɟɞɟɥɢɬɶ: ɤɨɧɟɱɧɵɣ ɨɛɴɟɦ,
ɤɨɧɟɱɧɭɸ ɬɟɦɩɟɪɚɬɭɪɭ, ɩɨɞɜɟɞɟɧɧɭɸ ɬɟɩɥɨɬɭ, ɚ ɬɚɤɠɟ ɪɚɛɨɬɭ, ɫɨɜɟɪɲɟɧɧɭɸ ɝɚɡɨɦ, ɟɫɥɢ
ɪɚɫɲɢɪɟɧɢɟ ɜ ɰɢɥɢɧɞɪɟ ɩɪɨɢɫɯɨɞɢɬ: 1) ɢɡɨɬɟɪɦɢɱɟɫɤɢ, 2) ɚɞɢɚɛɚɬɧɨ, 3) ɩɨɥɢɬɪɨɩɧɨ ɫ
ɩɨɤɚɡɚɬɟɥɟɦ ɩɨɥɢɬɪɨɩɵ
2,1 n
.
2.6. ȼɬɨɪɨɣ ɡɚɤɨɧ ɬɟɪɦɨɞɢɧɚɦɢɤɢ.
Ɉɫɧɨɜɧɵɟ ɮɨɪɦɭɥɵ.
ɂɧɬɟɝɪɚɥ Ʉɥɚɭɡɢɭɫɚ:
0
dq
T
d
³
Ɇɚɬɟɦɚɬɢɱɟɫɤɨɟ ɜɵɪɚɠɟɧɢɟ ɜɬɨɪɨɝɨ ɡɚɤɨɧɚ ɬɟɪɦɨɞɢɧɚɦɢɤɢ ɞɥɹ ɨɛɪɚɬɢɦɵɯ ɢ ɧɟɨɛɪɚɬɢɦɵɯ
ɩɪɨɰɟɫɫɨɜ:
