Burton T. (et. al.) Wind energy Handbook

Подождите немного. Документ загружается.

The values of the parameters in Equation (5.6) governing the resonant tip

response are determined as follows.

(a) The aerodynamic damping is assumed to be zero, so the damping logarithmic

decrement is taken as 0.05, corresponding to the structural damping value for

ﬁbreglass.

(b) The non-dimensional power spectral density of longitudinal wind turbulence,

(n) ¼ nS

)=

, is calculated at the blade ﬁrst mode natural frequency

according the Kaimal power spectrum deﬁned in Eurocode 1 (Appendix, Equa-

tion A5.8) as 0.0339.

tial expression for the normalized co-spectrum used in the derivation of the size

reduction factor, K

), in Equation (A5.25).

The various stages in the derivation of the extreme root bending moment and the

dynamic factor, Q

, are set out below. The ﬁgures in square brackets are the

corresponding values obtained using the method of Annex B of DS 472, which are

included for comparison.

Size reduction factor for resonant response, K

) 0.426 (Equation

(A5.25))

[0.312]

Ratio of standard deviation of resonant tip

displacement to the ﬁrst mode component of

steady tip displacement,

-0.6

-0.4

-0.2

0.2

0.4

0.6

0.8

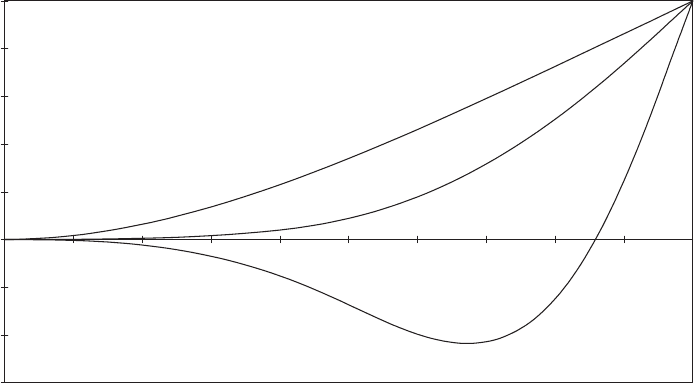
02468101214161820

Blade radius (m)

Displacement

First mode - blade of

constant

cross section

(for comparison)

First mode - tapered

blade ‘TR’

Second mode - tapered

blade ‘TR’

Figure 5.3 Blade ‘TR’ 1st and 2nd Mode Shapes

STATIONARY BLADE LOADING 225



¼ 2





ﬃﬃﬃﬃﬃﬃ

2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

)

(Equation

(5.6))

[N/A]

¼ 2 3 0:1225 3 9:935 3

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

0:0339

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

0:426

¼ 2 3 0:1225 3 9:935 3 0:184 3 0:652

¼ 2 3 0:1225 3 1:192 0.292

Root moment fact or, º

0.579 (Equation

(5.8))

[N/A]

Ratio of standard deviation of resonant root

moment to mean value,



0.169 (Equation

(5.7))

[0.338]

Size reduction factor for quasistatic or background

response, K

SMB

0.926 (Equation

(A5.40))

[0.78]

Ratio of standard deviation of quasistatic root

moment response to mean value,



¼ 2



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

SMB

¼ 2 3 0:1225 3 0:962 0.236

(Equation

(5.9))

[0.216]

Ratio of standard deviation of total root moment

response to mean value,



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ









ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

0:236

þ 0:169

0.290 [0.402]

Zero up-crossing frequency of quasistatic response,

0.41 Hz (Equation

(A5.57))

[N/A]

Zero up-crossing frequency of total root moment

response, 

1.02 Hz (Equation

(A5.54))

[N/A]

Peak factor, g, based on  3.74 (Equation

(5.12))

[3.9]

Ratio of extreme moment to mean value,

max

¼ 1 þ g





¼ 1 þ 3:74(0:290) 2.087 (Equation

(5.13))

[2.57]

Peak factor, g

, based on n

3.49 [3.5]

Ratio of quasista tic component of extreme moment

to mean value

¼ 1 þ g



¼ 1 þ 3:49(0:236) 1.823

(Equation

(5.15))

[1.76]

Dynamic factor, Q

¼ 2:087=1:823 1.145 (Equation

(5.17))

[1.46]

It is apparent that the DS 472 method yields a signiﬁcantly larger value of the

extreme root bending moment. However, the DS 472 ratio of extreme to mean

bending moment is intended to apply at all points along the blade, so a conservative

value at the root is inescapable, as is shown in the next section which examines the

variation of bending moment along the blade.

226 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

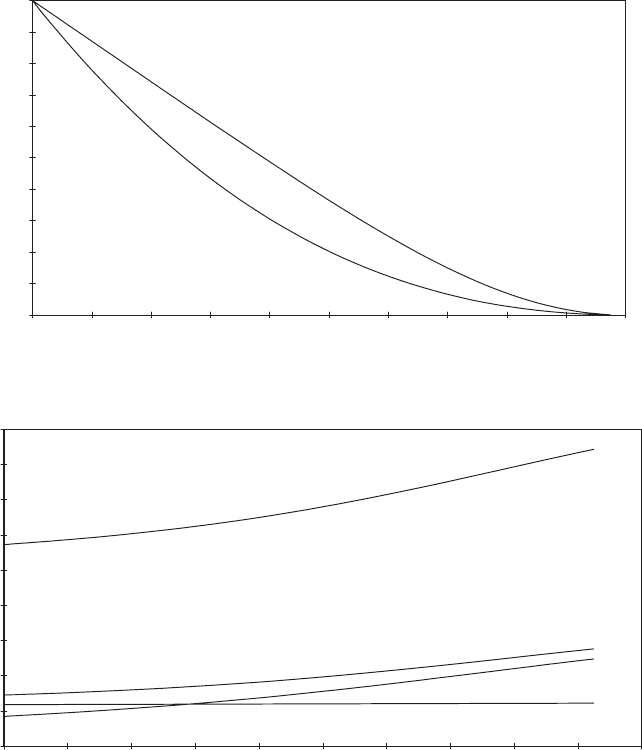
Spanwise variation of bending moment

The resonant and quasistatic components of bending moments at intermediate

positions along the blade can be related to those at the root in a straightforward way.

As far as the quasistatic bending moment ﬂuctuations are concerned, the varia-

tion along the blade follows closely the bending moment variation due to the steady

loading, although slight changes in the size reduction factor have a small effect. The

bending moment diagram for the resonant oscillations is, however, of a very

different shape, because of the dominance of the inertia loading on the tip. An

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Radius (r/R )

Moment at radius r as a proportion of root bending moment

Resonant bending moment

Quasistatic bending moment

Figure 5.4 Spanwise Variation of Resonant and Quasistatic Bending Moments – Blade ‘TR’

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Radius (r/R )

Quasistatic bending moment standard deviation/

steady bending moment

Resonant bending moment standard deviation/

steady bending moment

Combined bending moment standard deviation/

steady bending moment

Dynamic magnification factor

Figure 5.5 Spanwise Variation of (a) Fluctuating Bending Moment Standard Deviations in

Terms of Local Steady Bending Moment, and (b) Dynamic Magniﬁcation Factor – for Blade

‘TR’

STATIONARY BLADE LOADING 227

expression for the resonant bending moment variation along the blade is given in

Section A5.8 of the Appendix, and it is plotted out for the example above in Figure

5.4, with the quasistatic bending moment variation alongside for comparison. It is

seen that the resonant bending moment diagram is closer to linear than the

quasistatic one, which approximates to a parabola.

A consequence of the much slower decay of the resonant bending moment out

towards the tip is an increase in the ratio of the resonant bending moment standard

deviation to the local steady moment with radius. This results in an increase in the

dynamic magniﬁcation factor, Q

, from 1.145 at the root to 1.69 at the tip for the

example above (see Figure 5.5).

5.7 Blade Loads During Operation

5.7.1 Deterministic and stochastic load components

It is normal to separate out the loads due to the stea dy wind on the rotating blade

from those due to wind speed ﬂuctuations and analyse them in different ways. The

periodic loading on the blade due to the steady spatial variation of wind speed over

the rotor swept area is termed the deterministic load component, because it is

uniquely determined by a limited number of parameters – i.e., the hub-height wind

speed, the rotational speed, the wind shear, etc. On the other hand, the random

loading on the blade due to wind speed ﬂuctuations (i.e., turbulence) has to be

described probabilistically, and is therefore termed the stochastic load component.

In addition to wind loading, the rotating blade is also acted on by gravity and

inertial loadings. The gravity loading depends simply on blade azimuth and mass

distribution, and is thus det erministic, but the inertial loadings may be affected by

turbulence – as, for example, in the case of a teetering rotor – and so will sometimes

contain stochastic as well as deterministic components.

5.7.2 Deterministic Aerodynamic Loads

Steady, uniform ﬂow perpendicular to plane of rotor

The application of momentum theory to a blade element, which is described in

Section 3.5.3, enables the aerodynam ic forces on the blade to be calcu lated at

different radii. Equations (3.51) or (3.51a) and (3.52) are solved iteratively for the

ﬂow induction factors, a and a9, at each radiu s, enabling the ﬂow angle, , the angle

of attack, Æ, and hence the lift and drag coefﬁcients to be determined. The solution

of the equations is normally simpliﬁed by omitting the C

term in Equation (3.51) –

an approximation which is justifed, because 

is negligibly small away from

the root area.

For loadings on the outboar d portion of the blade, allowance for tip loss must be

made, so Equations (3.51) and (3.52) are replaced by Equations (3.51b) and (3.52a) in

Section 3.8.5, (with the omission of the C

term in Equation (3.51b) again being

228 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

permissible). These equations can be arranged to give the following expressions for

the forces per unit length on an element perpendicular to the plane of rotation and

in the direction of blade motion, known as the out-of-plane and in-plane forces

respectively:

Out-of-plane force per unit length: F

¼ C

c ¼ 4rU

(1  af )a

r (5:18)

In-plane force per unit length: F

¼ C

c ¼ 4rU

(1  af )a9

(5:19)

The parameters in the expressions are as deﬁned in Chapter 3 ( f is the tip loss

factor, and N is the number of blades), while the x and y directions are as deﬁned in

Figure C1.

The variation of the in-plane and out-of-plane forces with radius is shown in

Figure 5.6 for a typical machine operating in a steady 10 m=s wind speed. The 40 m

stall-regulated turbine considered in this example is ﬁtted with three ‘TR’ blades as

described in Example 5.1 and rotates at 30 r.p.m. The blade twist distribution is

linear, and selected to produce the maximum energy yield for an annual mean

wind speed of 7 m=s. It is evident that the out-o f-plane load per unit length

increases approximately linearly with radius, in spite of the reducing blade chord

until the effects of tip loss are felt beyond about 75 percent of tip radius. Note that

the form of the variation would be the same for any combi nation of rotational

speed, wind speed and tip radius yielding the same tip speed ratio, because it is the

tip speed ratio that determines the radial distribution of ﬂow angle , and of the

induction factors a and a9.

Integration of these forces along the blade then yields in-plane and out-of-plane

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

0 2 4 6 8 101214161820

Radius (m)

Load per metre (KN)

Out-of-plane force

per unit length

In-plane force

per unit length

Rotational speed = 30 rpm

Figure 5.6 Distribution of Blade In-plane and Out-of-plane Aerodynamic Loads during

Operation of Typical 40 m Diameter Stall-regulated Machine in a Steady, Uniform 10 m=s

Wind

BLADE LOADS DURING OPERATION 229

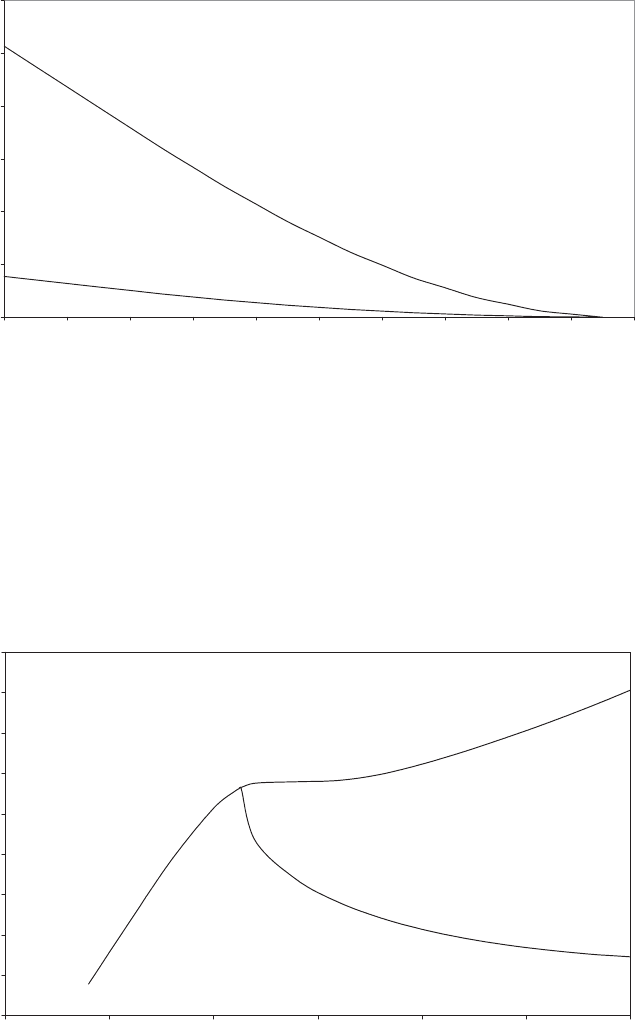
aerodynamic blade bending moments. The variation of these moments with radius

is shown in Figure 5.7 for the example above. The blade bending mo ments

effectively decrease linearly with increasing radius over the inboard third of the

blade because of the concentration of loading outboard.

The variation of the blade root out-of-plane bending moment with wind speed is

illustrated in Figure 5.8 for the 40 m diameter example machine described above.

100

150

200

250

300

0 2 4 6 8 101214161820

Radius (m)

Bending Moment (KNm)

Out-of-plane moment

In-plane moment

Rotational speed = 30 rpm

Figure 5.7 Blade In-plane and Out-of-plane Aerodynamic Bending Moment Distributions for

Typical 40 m Diameter Stall-regulated Machine Operating in a Steady, Uniform 10 m =s Wind

100

150

200

250

300

350

400

450

0 5 10 15 20 25 30

Wind speed (m/s)

Out-of-plane aerodynamic root bending moment (kNm)

500 kW Stall-regulated machine

Pitch-regulated machine

with 400 kW power limit

40 m diameter, 3 bladed rotor

with TR blades

rotational speed = 30 rpm

Figure 5.8 Blade Out-of-plane Root Bending Moment During Operation in Steady, Uniform

Wind – Variation with Wind Speed for Similar Stall-regulated and Pitch-regulated Machines

230

DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

As explained in Section 3.12, the phenomenon of stall delay results in signiﬁcantly

increased values of the lift coefﬁcient at higher wind speeds on the inboard section

of the rotating blade than predicted by static aerofoil data, such as that reproduced

in Figure 3.41. Accordingly, Figu re 5.8 and the other ﬁgures referred to in this

section have been derived using realistic aerofoil data for a rotating LM-19.0 blade

reported in Petersen et al. (1998), which is based on an empirical modiﬁcation of

static or two-dimensional aerofoil data. The modiﬁed data are reproduced in Figure

5.9, and display much higher lift coefﬁcients for the thicker, inboard blade sections

at high angles of attack than for the thinner, outboard blade sections because of stall

delay at the inboard sections.

Figure 5.8 shows the blade root out-of-plane bending moment increasing nearly

linearly with wind speed at ﬁrst and then levelling off, becoming almost constant

for winds between 12 m=s and 16 m =s, as the blade goes into stall. Thereafter the

root moment increases again, but much more gently than before.

Also shown on Figure 5.8 is the variation of blade root out-of-plane bending

moment with wind speed for the same machine with pitch regulation to limit the

power output to 400 kW. It is evident that the bending moment drops away rapidly

at wind speed s above rated.

Yawed ﬂow

The appli cation of blade element–momentum theory to steady yawed ﬂow is

decribed in Section 3.10.8. This methodology has been used to derive Figure 5.10,

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

0 5 10 15 20 25 30

Angle of attack

Lift and Drag Coefficients

Lift

Drag

t/c = 24%

t/c = 18%

t/c = 15%

t/c = 13%

t/c = 24%

t/c = 13%,

15%

and 18%

Figure 5.9 Aerofoil Data for LM-19.0 Blade for Various Thickness/Chord Ratios (from

Petersen et al. (1998))

BLADE LOADS DURING OPERATION 231

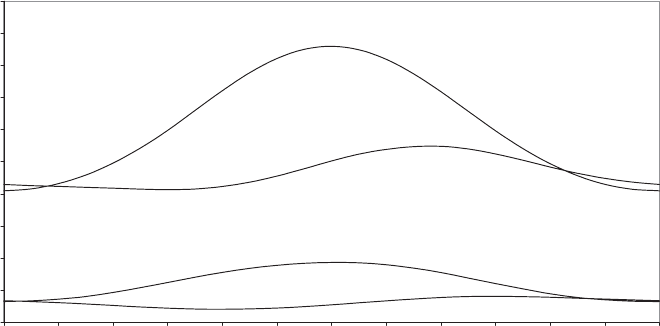
which shows the variation of the blade root out-of-plane and in-plane moments

with azimuth for the 40 m diameter stall-regulated machine described above,

operating at a steady yaw angle of þ308. Note that the blade azimuth is measured

in the direction of blade rotation, from a zero value at top dead centre, and the yaw

angle is deﬁned as positive when the lateral component of air ﬂow with respect to

the rotor disc is in the same direction as the blade movement at zero azimuth.

Figure 5.10 reveals a distinct difference between the behaviour at 10 m=s and

20 m=s. In the latter case, the bending moment variation is sinusoidal with a

maximum value at 1808 azimuth, indicating that the variation is dominated by the

effect of the ﬂuctuation of the air velocity relative the blade, W.At10m=s, however,

the maximum out-of-plane bending mome nt oc curs at about 2408 azimuth, suggest-

ing that the non-uniform component of induce d velocity, u

(Equation (3.107)) is

also signiﬁcant. As wind speed increases, of course, the induction factor, a, becomes

small, reducing the impact of u

Shaft tilt

Upwind machines, i.e., wind turbines with the rotor positioned between the tower

and the oncoming wind, normally have the rotor shaft tilted upwards by several

degrees in order to increase the clearance between the rotor and the tower. Thus, as

for the case of ya w misalignment, the ﬂow is inclined to the rotor shaft axis, but

tilted upwards rather than sideways, so the treatment of shaft tilt mirrors that of

yawed ﬂow.

100

150

200

250

300

350

400

450

500

0 30 60 90 120 150 180 210 240 270 300 330 360

Azimuth (degrees)

Aerodynamic Root Bending Moment (kNm)

Out-of-plane BM

In-plane BM

20 m/s wind speed

10 m/s wind speed

20 m/s wind speed

10 m/s wind speed

Figure 5.10 Variation of Blade Root Bending Moments with Azimuth, for Typical 40 m

Diameter Stall-regulated Machine Operating at a Steady 308 Yaw

232

DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

Wind shear

The increase of wind speed with height is known as wind shear. The theoretical

logarithmic proﬁle, U(z) / ln(z=z

), is usually approximated by the power law,

U(z) / (z=z

ref

)

for wind turbine design purposes. The appropriate value of the

exponent Æ increases with the surface roughness, z

, with a ﬁgure of 0.14 typically

quoted for level countryside, although the speed up of airﬂow close to the ground

over rounded hills usually results in a lower value at hill tops. As already noted,

IEC 61400-1 speciﬁes a conservative value of 0.20.

In applying momentum theory to this case, the velocity component at right angles

to the plane of rotation is expressed as U

(1 þ r cos ł=z

hub

)

(1  a). The variation of

blade root bending moments with azimuth due to wind shear is illustrated in

Figure 5.11 for the example 40 m diameter stall-regulated machine, taking the

exponent as 0.20, the hub height as 40 m and considering hub-height wind speeds

of 10 m=s and 15 m=s. In the former case, the variation is nearly sinusoidal, but in

the latter case the root bending moments are effectively constant, as the blade is in

stall.

Tower shadow

Blocking of the air ﬂow by the tower resu lts in regions of reduced wind speed both

upwind and downwi nd of the tower. This reduction is more severe for tubular

100

150

200

250

300

350

0 30 60 90 120 150 180 210 240 270 300 330 360

Azimuth (degrees)

Aerodynamic root bending moment (kNm)

Out-of-plane moment for U = 15 m/s

Out-of-plane moment for U = 10 m/s

In-plane moment for U = 15 m/s

In-plane moment for U = 10 m/s

Rotational speed = 30 r.p.m.

Shear exponent = 0.2

Hub height = 40 m

Figure 5.11 Variation of Blade Root Bending Moments with Azimuth due to Wind Shear,

for Typical 40 m Diameter Stall-regulated Machine Operating in Steady Hub-height Winds of

10 m=s and 15 m=s (shear exponent ¼ 0:2)

BLADE LOADS DURING OPERATION 233

towers than for lattice towers and, in the case of tubular towers, is larger on the

downwind side because of ﬂow separation. As a consequence, designers of down-

wind machines usually position the rotor plane well clear of the tower to minimize

the interference effect.

The velocity deﬁcits upwind of a tubular tower can be modelled using potential

ﬂow theory. The ﬂow around a cylindrical tower is derived by superposing a

doublet, i.e., a source and sink at very close spacing , on a uniform ﬂow, U

, giving

the stream function:

ł ¼ U

y 1 

(D=2)

þ y

(5:20)

where D is the tower diameter, and x and y are the longit udinal and lateral co-

ordinates with respect to the tower centre (see Figure 5.12). Differentiation of ł with

respect to y yields the following expression for the ﬂow velocity in the x direction:

U ¼ U

1 

(D=2)

 y

)

þ y

)

(5:21)

The second term with in the brackets, which is the velocity deﬁcit as a proportion of

the undisturbed wind speed, is plotted out against the lateral co-ordinate, y,

divided by tower diameter, for a range of upwind distances, x , in Figure 5.13. The

velocity deﬁcit on the ﬂow axis of symmetr y is equal to U

(D=2x)

and the total

width of the deﬁcit region is twice the upwind distance. Consequently the velocity

gradient encountered by a rotating blade decreases rapidly as the upwind distance,

x, increases.

The effect of tower shadow on blade loading can be estimated by setting the local

velocity component at right angles to the plane of rotation equal to U(1  a) in place

of U

(1  a), and applying blade element theory as usual. Results for blade root

bending moments for the example 40 m diameter stall-regulated mach ine are given

in Figure 5.14, assuming a tower diameter of 2 m and ignoring dynamic effects. The

plots show the variati on of in-plane and out-of-plane root moments with azimuth

during operation in wind speeds of 10 m=s and 15 m=s, for a blade-tower clearance

equal to the tower radius i.e., for x=D ¼ 1. Note that the dip in out-of-plane bending

moment is more severe at the lower wind speed. Also shown are 10 m=s plots for

x=D ¼ 1:5, which exhibit a much less severe disturbance.

In the case of downwind turbines, the ﬂow separation and generation of eddies

which take place are less amenable to analysis, so empirical methods are used to

estimate the mean velocity deﬁcit. Commonly the proﬁle of the velocity deﬁcit is

assumed to be of cosine form, so that

U ¼ U

1  k cos

y





(5:22)

234 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES