Бурова И.Г., Демьянович Ю.К. Алгоритмы параллельных вычислений и программирование
Подождите немного. Документ загружается.

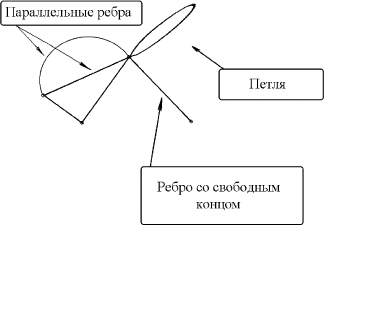
Циклом называется цепь, начало и конец которой находятся в
одной и той же вершине.
Цикл, образованный последовательностью ребер, среди вер-
шин которых не встречается одинаковых, называется элементар-
ным.
Граф называется связным, если любые две его вершины можно
соединить цепью.
Граф называется простым, если он не содержит петель и крат-
ных ребер.
Рис. 5. Граф с кратными ребрами и петлями.
Граф, содержащий кратные ребра, но без петель, называется
мультиграфом, а граф с кратными ребрами и петлями называет-
ся псевдографом (рис. 5). Граф, не содержащий ребер, называется
пустым.
§ 2. Ориентированный граф
До сих пор рассматривались неупорядоченные пары вершин
(т.е. неориентированные ребра). Но если порядок существен, то вво-
дят ориентацию.
Упорядоченную пару (u, v), u, v ∈ V , будем называть ориенти-
рованным ребром или дугой и будем говорить, что u — начальная
вершина, а v — конечная вершина, и что u предшествует v.
42

Если V — непустое множество вершин, а E — множество дуг
(ориентированных ребер), то G = (V, E) называется ориентирован-
ным графом (орграфом).
Ориентированный граф порождает (вообще говоря, неодно-
значное) отображение Γ вершин: если (u, v) — дуга, то по опре-
делению v = Γu, а если из вершины u не исходит ни одной дуги, то
полагают Γu = θ. Говорят, что отображение Γ задает отношение
предшествования.
Для ориентированных графов термины ребро, цепь, цикл,
связность обычно заменяются на термины дуга, путь, контур,
сильная связность.
Число дуг, образующих путь, называется длиной пути.
Простой путь (т.е. путь, не имеющий кратных ребер) макси-
мально возможной длины называется критическим путем графа.
Граф называется ациклическим, если он не имеет циклов.
Граф называется помеченным, если его вершины снабжены
некоторыми метками (например, номерами).
Иногда рассматривают частично упорядоченные графы, в ко-
тором лишь часть ребер имеет ориентацию.
Если на каком-либо этапе исследования для ориентированного
графа используется терминология, введенная для неориентирован-
ного графа, то это значит, что ориентация графа не принимается
во внимание.
§ 3. Топологическая сортировка
Вначале будем рассматривать графы без висячих ребер.
Теорема 3.1. В любом ориентированном ациклическом графе
существует хотя бы одна вершина, для которой нет предшеству-
ющей, и хотя бы одна вершина, для которой нет последующей.
Д о к а з а т е л ь с т в о. Если для каждой вершины графа есть
предшествующая, то ввиду конечности числа вершин в рассматри-
ваемом графе есть контур (цикл), а значит, он не ациклический.
Аналогично устанавливается второе утверждение. Теорема доказа-
на.
Дальше вершину графа будем помечать номером т.е. припи-
сывать ей то или иное натуральное число; вершину, помеченную
номером j будем обозначать v
j
.
43

Теорема 3.2. Пусть дан ориентированный ациклический
граф, имеющий n вершин. Существует такое натуральное чис-
ло s, s ≤ n, что все вершины графа можно пометить одним из
номеров 1, 2, . . . , s так, что если (v
i
, v
j
) — его дуга, то верно нера-
венство i < j.
Д о к а з а т е л ь с т в о. Выберем в графе вершины, которые не
имеют предшествующих, и пометим их индексом 1. Отбросим их
вместе с инцидентными им дугами. В полученном в результате этой
операции графе пометим цифрой 2 все вершины, которые не имеют
предшествующих, а затем отбросим их вместе с инцидентными им
дугами.
Повторяя последовательно эту операцию, придем к исчерпа-
нию графа (ввиду его конечности). Поскольку на каждом шаге от-
брасывается хотя бы одна вершина, то количество израсходованных
номеров 1, 2, . . . , s не более числа вершин n. Теорема доказана.
Следствие 3.1. При указанной в теореме 3.2 нумерации ни-
какие вершины с одним и тем же индексом не связаны дугой.
Обозначим s
n
минимальное количество индексов, которыми
можно пометить все вершины графа.
Следствие 3.2. Минимальное число индексов s
n
, которыми
можно пометить все вершины графа, на единицу больше длины
его критического пути.
Д о к а з а т е л ь с т в о. Возвращаясь к доказательству теоремы
3.2, видим, что на каждом шаге (за исключением последнего) от-
брасывается вершина, не имеющая предшествующей, вместе с ин-
цидентными ей дугами. Если у критического пути число звеньев
больше, чем таких операций отбрасывания, то поскольку все дуги
отбрасываются за s − 1 шаг, то на каком-то шаге отбрасывается бо-
лее одной дуги критического пути, а это означает, что на этом шаге
отбрасываются по крайней мере две соседние вершины критическо-
го пути, имеющие одинаковые номера. Однако, для рассматривае-
мой нумерации две соседние вершины не могут иметь одинаковые
номера (см. следствие 3.1). Итак, число звеньев критического пути
не больше числа s − 1.
С другой стороны, из алгоритма отбрасывания (см. доказа-
тельство теоремы 3.2) видно, что минимальное число индексов бу-
дет использовано, если при каждой операции отбрасывания будут
отбрасываться все вершины (вместе с инцидентными им дугами),
не имеющие предшествующей (такие операции отбрасывания назы-
44

ваются максимальными). При последовательности максимальных
отбрасываний начало любого пути может встретиться только на
первом шаге операции. Это означает, что на каждом шаге опера-
ции (за исключением последней) обязательно отбрасывается строго
одна дуга критического пути графа. Этот путь не может закончить-
ся раньше завершения всех отбрасываний, ибо тогда он не был бы
критическим путем графа. Это означает, что число отбрасываний
(вместе с последним) в точности на единицу больше длины крити-
ческого пути графа.
Следствие 3.3. Для любого натурального числа s, s
n
≤ s ≤
n, существует такая разметка вершин графа, при которой ис-
пользуются все s индексов.
Д о к а з а т е л ь с т в о легко вытекает из следствий 3.1 и 3.2.
Определение 3.1. Разметка вершин графа, удовлетворяю-
щая условиям теоремы 3.2, называется сортировкой графа.
Определение 3.2. Разметка вершин графа, проведенная при
максимальных операциях отбрасывания, называется топологиче-
ской сортировкой графа.
Нетрудно заметить следующее.
1. При топологической сортировке все пути могут начинаться
лишь в вершинах с индексом k; вершины с индексом k > 1 не могут
служить началом пути.
2. При сортировке вершина с индексом k > 1 может являться
концом пути длины не более k − 1.
3. При топологической сортировке в вершине с индексом k > 1
могут заканчиваться лишь пути длины k − 1.
4. При топологической сортировке число используемых индек-
сов на единицу больше длины критического пути графа.
Определение 3.3. Топологическая сортировка называется
линейной, если индексы любых вершин различны; в этом случае
говорят, что граф линейно упорядочен.
Замечание. Если топологическая сортировка не является ли-
нейной, то из нее можно получить другие сортировки с б´ольшим
числом индексов.
Д о к а з а т е л ь с т в о этого замечания очевидно.
§ 4. Примеры графов параллельных форм
Рассмотрим процесс вычисления выражения (a
1
a
2
+
a
3
a
4
)(a
5
a
6
+ a
7
a
8
) и построим для него графы нескольких
45
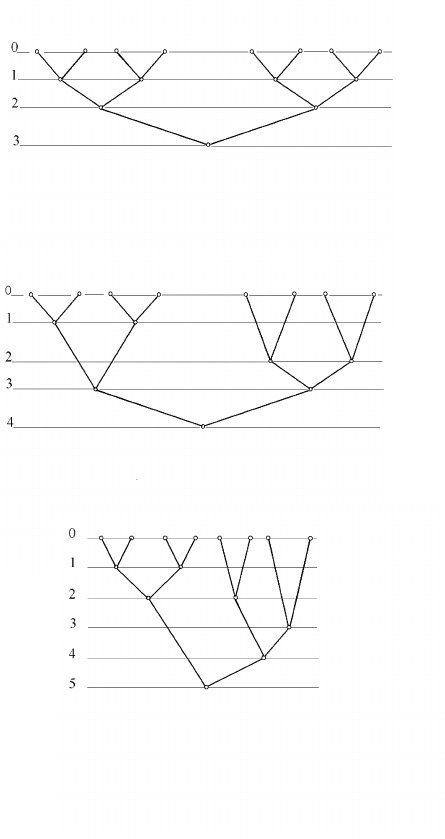
параллельных форм (эти параллельные формы уже рассматрива-
лись нами ранее). Соответствующие графы будем иллюстрировать
рисунками 1.6 – 1.8; на них данные помещены на нулевой уровень.
Первая параллельная форма (см. рис. 6)
Данные 0: a
1
, a
2
, a
3
, a
4
, a
5
, a
6
, a
7
, a
8
.
Ярус 1. a
1
a
2
, a
3
a
4
, a
5
a
6
, a
7
a
8
.
Ярус 2. a
1
a
2
+ a
3
a
4
, a
5
a
6
+ a
7
a
8
.
Ярус 3. (a
1
a
2
+ a
3
a
4
)(a
5
a
6
+ a
7
a
8
).
Рис. 6. Первая параллельная форма.
Рис. 7. Вторая параллельная форма.
Рис. 8. Третья параллельная форма.
46
Вторая параллельная форма (см. рис. 7)
Данные 0: a
1
, a
2
, a
3
, a
4
, a
5
, a
6
, a
7
, a
8
.
Ярус 1. a
1
a
2
, a
3
a
4
.
Ярус 2. a
5
a
6
, a
7
a
8
.
Ярус 3. a
1
a
2
+ a
3
a
4
, a
5
a
6
+ a
7
a
8
.
Ярус 4. (a
1
a
2
+ a
3
a
4
)(a
5
a
6
+ a
7
a
8
).
Третья параллельная форма (см. рис. 8)
Данные 0: a
1
, a
2
, a
3
, a
4
, a
5
, a
6
, a
7
, a
8
.
Ярус 1. a
1
a
2
, a
3
a
4
.
Ярус 2. a
1
a
2
+ a
3
a
4
, a
5
a
6
.
Ярус 3. a
7
a
8
.
Ярус 4. a
5
a
6
+ a
7
a
8
.
Ярус 5. (a
1
a
2
+ a
3
a
4
)(a
5
a
6
+ a
7
a
8
).
Нетрудно видеть, что все три графа отличаются друг от друга
лишь топологической сортировкой, что и должно быть при изобра-
жении одного и того же алгоритма.
§ 5. Изоморфизм графов. Операции гомоморфизма
Определение 5.1. Два графа (соответственно, ориенти-
рованных графа) называются изоморфными, если между множе-
ствами вершин и ребер (вершин и дуг) можно установить вза-
имно однозначное соответствие, сохраняющее отношение инци-
денции (соответственно, отношение инциденции и ориентацию).
Изоморфизм графов представляет собой эквивалентность (т.е.
отношение со свойствами рефлексиности, симметричности и тран-
зитивности).
Определение 5.2. Подграфом графа G называется граф, у
которого все вершины и все ребра принадлежат G (для них сохра-
няются прежние отношения инциденции). Подграф, у которого
вершины те же, что и у G, называется остовным подграфом для
G.
Определение 5.3. Объединением графов G
1
= (V
1
, E
1
) и G
2
=
(V
2
, E
2
) называется граф
G
3
= (V
1
∪ V
2
, E
1
∪ E
2
).
47
Пересечением графов G
1
= (V
1
, E
1
) и G
2
= (V
2
, E
2
) называется
граф
G
4
= (V
1
∩ V
2
, E
1
∩ E
2
).
Легко видеть, что операции объединения и пересечения графов
ассоциативны и коммутативны.
В графе G = (V, E) выберем две вершины u, v ∈ V и построим
новый граф G
0
= (V
0
, E
0
), где множество V
0
получается из V отож-
дествлением вершин u и v. Результат отождествления — новую вер-
шину, обозначим w (w — символ, не встречавшийся в обозначении
вершин графа G),
V
0
= V \ {u, v} ∪ w ,
а E
0
получается из E заменой всех ребер вида (u, v
1
) на ребра
(w, v
1
), а затем всех ребер вида (u
1
, v) на ребра (u
1
, w) — для неори-
ентированного графа; для ориентированного графа, кроме этого,
требуется заменить все ребра вида (v
1
, u) на ребра (v
1
, w), а также
все ребра вида (v, u
1
) на ребра (w, u
1
).
Определение 5.4. Говорят, что граф G
0
получен из графа G
кратным элементарным гомоморфизмом.
Определение 5.5. По введенному в предыдущем определе-
нии графу G
0
построим граф G
00
исключением из G
0
всех кратных
ребер и петель. Говорят, что граф G
00
получен из G простым эле-
ментарным гомоморфизмом.
Определение 5.6. Последовательное выполнение операций
(простого) элементарного гомоморфизма называется операцией
(простого) гомоморфизма.
Говорят, что граф H гомоморфен (просто гомоморфен) графу
G, если он изоморфен графу, полученному из G операцией (про-
стого) гомоморфизма. Вершина графа H, соответствующая отож-
дествляемым вершинам графа G, называется их образом, а отож-
дествляемые вершины (графа G) — прообразом при рассматривае-
мом гомоморфизме. Сам граф H называется гомоморфным образом
графа G.
Определение 5.7. Гомоморфизм называется независимым,
если никакие две из отождествляемых вершин не соединены реб-
ром.
Определение 5.8. Гомоморфизм называется связным, если
подграф, образованный отождествляемыми вершинами, связен.
48

Теорема 5.1. Любой гомоморфизм можно представить как
последовательность независимых и связных гомоморфизмов.
Д о к а з а т е л ь с т в о вытекает из введенных только что поня-
тий (см. определения 5.7 и 5.8).
Замечание. Рассматривают также обратную задачу — задачу
о построении гомоморфного прообраза данного графа. Эта зада-
ча решается добавлением новых вершин и ребер. В связи с этим
вводят операцию добавления новых вершин: в E ребро (u, v) исход-
ного графа заменяют парой ребер (u, w), (v, w), а к V добавляют
новую вершину w. Возможны и другие способы добавления новых
вершин, которые ведут к получению гомоморфного прообраза ис-
ходного графа.
§ 6. Построение графов параллельных форм
Предположим, что известны:
— множество переменных, преобразование которых составляет
рассматриваемый алгоритм;
— множество операций, выполняемых при реализации алгорит-
ма;
— соответствие, показывающее, какие результаты предшеству-
ющих операций являются операндами для следующих.
Дополнительные предположения:
1) число операндов в каждой операции фиксировано и не зави-
сит от результатов работы алгоритма;
2) классы переменных и классы операций фиксированы; пе-
ременные и операции, принадлежащие этим классам, называются
базовыми.
Построение графа алгоритма состоит в следующем:
— каждой операции U алгоритма ставится в соответствие вер-
шина u,
— если операнд операции V (которой поставлена в соответствие
вершина v) является результатом операции U, то соответствующие
им вершины u и v соединяются направленной (от u к v) дугой (u, v).
Полученный таким образом граф имеет следующие свойства:
— в каждую вершину u входит столько дуг, сколько входов у
операции U,
— полученный граф не содержит циклов.
Результатом является ориентированный ациклический мульти-
граф.
49
Определение 6.1.Пусть задан алгоритм и G = (V, E) его
граф. Рассмотрим V
1
, . . . , V
k
— непересекающиеся подмножества
его вершин,
V =
k
[
i=1
V
i
, V
i
∩ V
j
= ∅, i 6= j, (6.1)
такие, что если u ∈ V
i
, v ∈ V
j
и существует дуга (u, v) ∈ E, то
i < j. В этом случае представление (6.1) называется параллель-
ной формой алгоритма, а множества V
1
, V
2
, . . . , V
k
— его ярусами.
Число k называется высотой параллельной формы; число |V
j
|
элементов множества V
j
называется шириной j-го яруса V
j
, а мак-
симальное из чисел |V
j
| — шириной параллельной формы.
Параллельная форма минимальной высоты называется макси-
мальной.
Высотой алгоритма называется высота максимальной парал-
лельной формы.
Ширина максимальной параллельной формы называется ши-
риной алгоритма.
Параллельная форма ширины 1 называется последовательной.
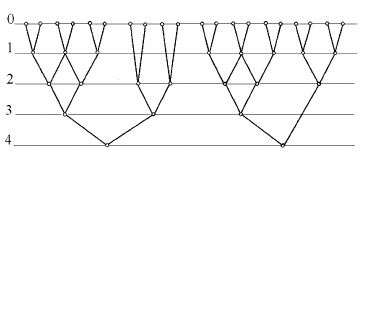
Максимальная параллельная форма называется канонической,
если через каждую вершину i-го яруса проходит путь длины i − 1.
На рис. 9 представлены неканоническая (слева) и каноническая
(справа) параллельные формы.
Рис. 9. Неканоническая и каноническая параллельные формы.
Отметим некоторые свойства графов параллельных форм:
1) никакие две вершины одного яруса не связаны дугой;
2) все дуги, входящие в вершины первого яруса, являются реб-
рами с одной вершиной (лежащей в первом ярусе);
50
3) все дуги, исходящие из вершин последнего яруса, являются
ребрами с одной вершиной (лежащей в последнем ярусе);
4) высота параллельной формы на единицу больше критиче-
ского пути графа;
5) произведение высоты параллельной формы на ее ширину не
меньше числа вершин графа.
В силу предыдущих рассуждений эти свойства представляются
достаточно очевидными.
Замечание.На первый взгляд может показаться, что отыскание
параллельной формы не требует большого числа операций. Дей-
ствительно, при топологической сортировке требуется число дей-
ствий по меньшей мере порядка n
2
(ибо на каждом шаге прихо-
дится делать сравнения со всеми оставшимися вершинами), и это
кажется приемлемым с точки зрения сложности алгоритмов (закон
полиномиальный и даже весьма малой степени — квадратичный).
Однако в реальных алгоритмах общее число n операций велико и
потому даже линейная зависимость от n для отыскания параллель-
ной формы обычно недопустима (ибо в наших обстоятельствах, как
правило, не получится никакой экономии). Поэтому нужны более
эффективные методы отыскания параллельных форм.
§ 7. Направленные графы и параллельные формы
Пусть задан ациклический ориентированный граф алгоритма,
вершины которого расположены в некотором арифметическом про-
странстве R
s
(т.е. в некотором евклидовом пространстве конечной
размерности s).
Теорема 7.1. Пусть в R
s
существует ось l (т.е. направ-
ленная прямая) такая, что ортогональная проекция графа на нее
имеет следующее свойство: ненулевые проекции всех его дуг име-
ют положительное значение. Тогда длина критического пути гра-
фа не превосходит суммы длин критических путей его подграфов,
проектирующихся в точки, и длины критического пути проекции
графа.
Д о к а з а т е л ь с т в о. Рассмотрим критический путь графа. Те
его части, которые имеют ненулевые проекции на ось, в сумме не
превосходят критического пути графа на оси. Те же его части, кото-
рые находятся в подграфах на ортогональных плоскостях, не пре-
восходят критических путей упомянутых подграфов. Складывая
51
