Бурова И.Г., Демьянович Ю.К. Алгоритмы параллельных вычислений и программирование

Подождите немного. Документ загружается.

Используя здесь алгоритм сдваивания, можно вычислить все про-

изведения Y

(с учётом того, что здесь s + 1 сомножитель) за

dlog

(s + 1)e макротактов, используя

s+1

макропроцессоров, вы-

полняющих в качестве макрооперации перемножение двух матриц

порядка nr + 1.

Согласно теореме 2.2 для перемножения двух матриц порядка

nr + 1 можно построить параллельную форму высоты dlog

(nr +

1)e + 1 и ширины (nr + 1)

Поэтому общая высота получаемой параллельной формы

h = dlog

(s + 1)e · (dlog

(nr + 1)e + 1), (4.7)

а её ширина

w =

s + 1

· (nr + 1)

. (4.8)

Теорема доказана.

Замечание. Рекуррентные соотношения вида (4.3) широко ис-

пользуются в численном анализе для проведения итерационных

процессов (в частности, при n = 1 эти соотношения превращаются в

числовые). Параллельная форма, полученная из них на основании

представлений (4.4)–(4.7), эквивалентна соотошениям (4.3) толь-

ко при условии точных вычислений. Ошибки округления, возни-

кающие при численных расчетах с плавающей точкой, могут суще-

ственно повлиять на результаты вычислений и привести к неустой-

чивости вычислительного процесса. Поэтому такой параллельной

формой следует пользоваться с большой осторожностью.

§ 5. Об LU-разложении

Рассмотрим квадратную матрицу A = (a

)

i,j=1,...,n

. Обозна-

чим A

квадратную матрицу, образованную пересечением первых

k строк и первых k столбцов матрицы A, A

= (a

)

i,j=1,...,k

, где

1 ≤ k ≤ n; в частности, матрица A

состоит из одного элемента a

= (a

), а A

= A. Определители detA

, k = 1, . . . , n, называют-

ся главными минорами матрицы A.

Теорема 5.1. Квадратная матрица A с ненулевыми главны-

ми минорами однозначно представляется в виде произведения LU

нижнетреугольной матрицы L с единицами на главной диагона-

ли и верхнетреугольной матрицы U , главная диагональ которой

состоит из ненулевых элементов.

Д о к а з а т е л ь с т в о. По условию теоремы

detA

6= 0, k = 1, 2, . . . , n. (5.1)

Доказательство теоремы проведём индукцией по k. При k = 1 оче-

видно

) = (1) · (a

), (5.2)

так что рассматривая одноэлементные матрицы L

= (1), U

), из (5.2) получим A

= L

. Итак, база индукции установле-

на.

Пусть теперь при некотором k, k ∈ {1, 2, . . . , n − 1}, известно,

что

= L

, (5.3)

где L

= (l

(k)

) — нижнетреугольная матрица порядка k с единица-

ми на главной диагонали, а U

— верхнетреугольная матрица того

же порядка, U

= (u

(k)

). Ввиду определения матрицы L

имеем

detL

= 1, а из неравенства (5.1) и свойства detA

= detL

· detU

получаем detU

6= 0. Итак,

detL

= 1, detU

6= 0. (5.4)

Представим матрицу A

k+1

в клеточной форме

k+1

a a

k+1 k+1

где a

k+1 k+1

— элемент исходной матрицы A, a — k-мерная вектор-

строка, b — k-мерный вектор-столбец.

Будем находить k-мерную вектор-строку l и k-мерный вектор-

столбец u, а также элемент u

k+1,k+1

из уравнения

l 1

¶µ

0 u

k+1 k+1

a a

k+1 k+1

. (5.5)

Соотношения (5.5) эквивалентны равенствам

= A

, L

u = b, lU

= a, (5.6)

l · u + u

k+1 k+1

= a

k+1 k+1

, (5.7)

где l·u — скалярное произведение векторов l и u. Первое из равенств

(5.6) заведомо верно, ибо совпадает с (5.3), второе представляет со-

бой систему линейных уравнений с неособенной матрицей L

(см.

(5.4)); отсюда однозначно определяется вектор u. Третье из соотно-

шений (5.6) являются системой линейных алгебраических уравне-

ний относительно компонент вектора l; благодаря второй формуле

в (5.4) вектор l определяется однозначно. Таким образом, в (5.7) l

и u уже определены; поэтому имеем

k+1,k+1

= a

k+1 k+1

− l · u.

Если положить

k+1

l 1

, U

k+1

0 u

k+1 k+1

то (5.5) принимает вид

k+1

= L

k+1

Шаг индукции завершен; вместе с базой индукции это завершает

доказательство. Теорема доказана.

Замечание.С помощью метода индукции аналогичным обра-

зом нетрудно установить, что если матрица A — ленточная матри-

ца, удовлетворяющая условиям теоремы, то матрицы L и U также

можно рассматривать как ленточные, ширина ленты которых не

больше, чем ширина ленты у матрицы A. Если A — диагональная,

то L и U — тоже диагональные.

§ 6. Распараллеливание LU-разложения

трехдиагональной матрицы

Пусть решается система линейных алгебраических уравнений

с трехдиагональной матрицей A:

A =







0 . . . 0 0 0

. . . 0 0 0

. . . . . . . . . . . . . . . . . . . . .

0 0 0 . . . a

k−1 k−2

k−1 k−1

k−1 k

0 0 0 . . . 0 a

k k−1

k k







Предположим, что A имеет ненулевые главные миноры. В со-

ответствии с теоремой об LU -разложении матрицы A будем иметь

A = BC,

где

B =







1 0 . . . 0 0

1 . . . 0 0

. . . . . . . . . . . . . . .

0 0 . . . b

k k−1







C =







0 . . . 0 0

0 c

. . . 0 0

. . . . . . . . . . . . . . . . . .

0 0 0 . . . c

k−1 k−1

k−1 k

0 0 . . . 0 0 c

k k







Получим формулы для элементов матриц B и C. Для упроще-

ния вычислений рассмотрим случай k = 4. Имеем

B =







1 0 0 0

1 0 0

0 b

1 0

0 0 b













0, 0

0 c

0 0 c

0 0 0 c







так что

BC =







0 0

+ c

0 b

+ c

0 0 b

+ c







Из равенства A = BC получаем формулы

= a

, c

= a

, c

= a

− b

, c

= a

, c

= a

− b

= a

, b

= a

, c

= a

− b

В общем случае можно показать, что справедливы формулы

1,1

= a

1,1

i−1,i

= a

i−1,i

, (6.1)

i,i−1

= a

i,i−1

i−1,i−1

, (6.2)

i,i

= a

i,i

− b

i,i−1

i−1,i

, (6.3)

где i = 2, 3, . . . , k (здесь и далее для ясности при отделении индексов

применяется запятая).

Умножая соотношение (6.3) на c

i−1,i−1

, находим

i,i

i−1,i−1

= a

i,i

i−1,i−1

− b

i,i−1

i−1,i

i−1,i−1

Используя в последнем произведении формулу (6.2), получаем

i,i

i−1,i−1

= a

i,i

i−1,i−1

− a

i−1,i

i,i−1

(6.4)

Пусть

= c

i,i

i−1,i−1

. . . c

2,2

1,1

, i = 1, 2, . . . , k.

При i ≥ 3 умножим равенство (6.4) на q

i−2

; имеем

i,i

i−1,i−1

i−2

= a

i,i

i−1,i−1

i−2

− a

i−1,i

i−2

так что

= a

i,i

i−1

− a

i−1,i

i,i−1

i−2

, i = 3, 4, . . . , k. (6.5)

Преобразуем (6.5) к рекуррентным соотношениям (4.3),

= A

j,1

j−1

+ . . . + A

j,r

j−r

+ B

, j = 1, 2, . . . , s, (6.6)

полагая в них n = 1, т.е. считая, что X

, A

s,j

, B

— некоторые

числа.

Для этого в формулах (6.5) возьмем j = i − 2 и перепишем их

с использованием индекса j, j = 1, 2, . . . , k − 2. Получаем

j+2

= a

j+2,j+2

j+1

− a

j+1,j+2

j+2,j+1

. (6.7)

Теперь применим (6.6), полагая X

= q

j+2

, A

j,1

= a

j+2,j+2

, A

j,2

−a

j+1,j+2

j+2,j+1

, B

= 0, s = k − 2, r = 2.

Согласно формулам (4.7),(4.8) для рассматриваемого рекур-

рентного процесса существует параллельная форма высоты h =

dlog

(s + 1)e(dlog

(nr + 1)e + 1) и ширины w = d

s+1

e(nr + 1)

. Под-

ставляя сюда n = 1, s = k − 2 и r = 2, видим, что доказано следу-

ющее утверждение.

Теорема 6.1 LU-разложение трехдиагональной матрицы

k-го порядка можно осуществить параллельной формой высоты

3dlog

(k − 1)e и ширины 27d

k−1

Теперь рассмотрим распараллеливание процесса решения си-

стемы линейных алгебраических уравнений с трехдиагональной

матрицей.

Теорема 6.2. Решение системы k уравнений Ax = y с

трехдиагональной матрицей A можно осуществить параллель-

ной формой высоты O(log

k) и ширины O(k).

Д о к а з а т е л ь с т в о. Пусть получено LU-разложение матри-

цы A вида A = BC; тогда решение системы Ax = y получается

последовательным решением двух систем

Bz = y, Cx = z

с двухдиагональными матрицами (этот процесс соответсвует обрат-

ному ходу в методе Гаусса). После деления во второй системе на

диагональные элементы (один такт) решение сводится к рекуррент-

ному процессу (4.3). Действительно, для первой из систем имеем











= y

+ z

= y

+ z

= y

. . . . . . . . . . . . . . . . . .

ii−1

i−1

+ z

= y

. . . . . . . . . . . . . . . . . .

k,k−1

k−1

+ z

= y

откуда











= y

− b

= y

− b

. . . . . . . . . . . . . . . . . .

= y

− b

ii−1

i−1

. . . . . . . . . . . . . . . . . .

= y

− b

k,k−1

k−1

Применим рекуррентный процесс(4.1) – (4.3), полагая

n = 1, X

= 0, X

= z

, B

= y

, , j = 1, 2, . . . , k,

s = k, r = 1, A

= 0, A

= −b

i,i−1

, i = 2, 3, . . . , k.

Используя теорему 4.2, получаем параллельную форму для отыска-

ния чисел z

, i = 1, 2, . . . , k с высотой h = 2dlog

(k +1)e и с шириной

w = 8d

k+1

Такой же результат получается и для второго уравнения. С

учетом теоремы 6.1 видим, что решение системы k уравнений с

трехдиагональными матрицами k-го порядка можно осуществить

параллельной формой с высотой O(log

k) и с шириной O(k ), что и

требовалось доказать.

Замечание 1. Полученная параллельная форма основана на

методе Гаусса: LU-разложение соответствует прямому ходу, а реше-

ние систем с треугольными матрицами — обратному ходу. Однако,

характеристики устойчивости этой формы отличаются от устойчи-

вости обычно рассматриваемых последовательных алгоритмов ме-

тода Гаусса.

Замечание 2. Параллельных форм с меньшей (по порядку)

высотой, чем O(log

k) не существует.

Нетрудно установить справедливость следующего утвержде-

ния.

Теорема 6.3. Для решения системы линейных алгебраиче-

ских уравнений с треугольной матрицей порядка n существует

параллельная форма с высотой O(log

n) и шириной O(n

Д о к а з а т е л ь с т в о предлагается провести читателю самосто-

ятельно.

§ 7. О распараллеливании процесса

отыскания обратной матрицы

Рассмотрим задачу вычисления обратной матрицы A

−1

для

квадратной матрицы A порядка n. Для ее построения использу-

ем теорему Гамильтона–Кэли.

Пусть

f(λ) = λ

+ c

n−1

+ . . . + c

(7.1)

— характеристический многочлен матрицы A. Согласно теореме

Гамильтона–Кэли подстановка матрицы A в характеристический

многочлен получается нулевая матрица; этот факт записывается в

виде f (A) = 0 (здесь нулем обозначена квадратная нулевая матри-

ца порядка n). Отсюда (умножением на A) находим

−1

= −

n−1

+ c

n−2

+ . . . + c

n−1

, (7.2)

где E — единичная матрица.

Пусть λ

— корни характеристического уравнения, а s

— сум-

ма их k-х степеней

i=1

. (7.3)

Известно соотношение Ньютона (см., например, Курош А.Г. Курс

высшей алгебры. М., 1952):







1 0 0 . . . 0 0

2 0 . . . 0 0

3 . . . 0 0

. . . . . . . . . . . . . . . . . .

n−1

n−2

n−3

. . . s













. . .













−s

. . .

−s







. (7.4)

Числа s

можно вычислить, как сумму диагональных элемен-

тов матрицы A

Построение параллельной формы для определения матрицы

−1

сводится к следующим этапам:

1. Сначала по схеме сдваивания находят все степени матрицы до

n; это требует выполнения O(log

n) макрошагов, на каждом

из которых выполняется O(n) произведений двух квадратных

матриц порядка n. Поскольку произведение двух таких мат-

риц требует параллельной формы высоты dlog

ne+1 и шири-

ны n

, то отыскание степеней матрицы A от 2 до n − 1 может

быть произведено с помощью параллельной формы высоты

O(log

n) и ширины O(n

2. На втором этапе вычисляются все числа s

, как следы мат-

риц A

, k = 1, . . . , n; поскольку след — сумма диагональных

элементов, то требуется вычислить n сумм с n слагаемыми.

Это можно сделать по схеме сдваивания параллельной фор-

мой высоты O(log n) и ширины O(n

3. Теперь отыскиваются коэффициенты c

характеристическо-

го многочлена решением системы n-го порядка с треугольной

матрицей (см. (7.4)); благодаря теореме 6.3 это можно сделать

с помощью параллельной формы высоты O(log

n) и ширины

O(n

4. На четвертом этапе вычисляется матрица A

−1

по формуле

(7.2) с использованием схемы сдваивания (для всех n

элемен-

тов одновременно) с помощью параллельной формы высотой

O(log

n) и шириной O(n

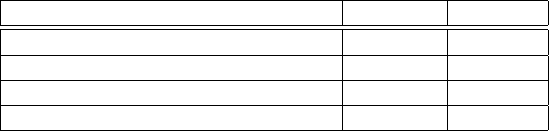
Для наглядности результаты представим в таблице.

Содержание этапа Высота Ширина

Вычисление степеней A

, . . . , A

O(log

n) O(n

)

Вычисление следов s

, k = 1, . . . , n O(log

n) O(n

)

Вычисление коэффициентов c

O(log

n) O(n

)

Вычисление матрицы A

−1

O(log

n) O(n

)

Из предыдущих рассуждений и приведенной таблицы видно,

что доказано следующее утверждение.

Теорема 7.1. Для вычисления обратной матрицы n-го по-

рядка существует параллельная форма высоты O(log

n) и шири-

ны O(n

Глава 3. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

ГРАФОВ В СВЯЗИ С РАСПАРАЛЛЕЛИВАНИЕМ

§ 1. О понятии графа

Рассмотрим конечное множество V с выделенным элементом θ.

Элементы множества V будем называть вершинами, а выделенный

элемент θ — пустой вершиной.

Вершины из V будем обозначать буквами u, v, w. Пусть E неко-

торое множество неупорядоченных пар (u, v), где u, v ∈ V . Пары

(u, v) называются ребрами; среди них пары вида (u, θ) и (θ, v) на-

зываем ребрами с одной вершиной, пары вида (u, u) называются

петлей.

Если V содержит не менее двух элементов и задано множество

E, то говорят, что задан граф; обозначим его G:

G = (V, E). (6.1)

Обычно граф изображается в виде некоторой схемы на плос-

кости или в пространстве, причем вершины графа изображаются

точками, а ребра — непрерывной линией, соединяющей вершины.

Ребра с одной вершиной изображаются в виде линии, исходящей из

этой вершины, со свободным концом. Ребра (u, v), повторяющиеся в

E, изображаются различными простыми кривыми, соединяющими

u и v.

Говорят также, что ребро (u, v) соединяет вершины u и v; при

этом сами вершины u, v называются смежными, а ребро (u, v) на-

зывают инцидентным вершинам u и v; вершины u, v также назы-

вают инцидентными ребру (u, v).

Все ребра с одинаковыми концевыми вершинами называются

кратными или параллельными. Некратные ребра называют различ-

ными. Ребро с совпадающими концевыми точками называется пет-

лей. Число инцидентных вершине ребер называется степенью вер-

шины. Вершина степени 1 называется висячей, а степени 0 — изо-

лированной. Ребро, инцидентное одной вершине, будем называть

висячим.

Если имеется упорядоченная последовательность вершин, каж-

дые две из которых являются смежными, то связывающую их по-

следовательность ребер называют цепью. Цепь называется про-

стой, если среди составляющих ее ребер нет кратных, и составной

— в противном случае.