Булашев С.В. Статистика для трейдеров

Подождите немного. Документ загружается.

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

Оптимальное число столбцов должно зависеть не только от

объема выборки, как это указано в большинстве пособий по

статистике. Очевидно, что это число зависит еще и от формы

распределения. Действительно, если плосковершинные

распределения можно приблизить достаточно малым

количеством столбцов, то для островершинных распределений с

их длинными, пологими спадами это количество естественно

должно быть больше.

Количество интервалов группировки должно быть

нечетным числом. При четном числе столбцов область вблизи

центра распределения будет описываться двумя симметрично

расположенными относительно центра столбцами гистограммы,

тем самым пик распределения будет неоправданно

сглаживаться. Это особенно критично для островершинных

распределений. Как уже говорилось выше, три столбца дают

очень мало информации о форме распределения. Поэтому будем

считать, что количество столбцов гистограммы должно быть

нечетным числом не менее пяти.

Эмпирическая формула для оценки оптимального

количества столбцов гистограммы как функции от объема

выборки

N и эксцесса

, пригодная к применению для

широкого класса распределений следующая:

4.0

5.1

Вычисленное по этой формуле значение должно быть

округлено вниз до ближайшего большего или равного пяти

нечетного целого.

Используя значение L , ширину столбца гистограммы

можно найти по формуле:

|)max(|2 −

6.3. Построение гистограммы распределения.

Изложим алгоритм построения гистограммы по выборке

случайных величин

Nkx

,...,1},{

1) Упорядочить исходную выборку по возрастанию.

2) Вычислить оценки центра распределения:

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

медиана

, Х

центр_сгибов

%50

X , Х

центр_размаха

Упорядочить эти оценки по возрастанию и выбрать из них в

качестве центра распределения серединное, то есть третье

по счету, значение, которое обозначить как Х

ЦЕНТР.

3) Вычислить оценку среднеквадратичного отклонения

)(

ЦЕНТР

−

∑

4) Вычислить оценку эксцесса

)3)(2(

)1)(32(3

)(

)3)(2)(1(

321

−−

−

−−

−−−

+−

⋅=

∑

NNN

Хx

NNN

ЦЕНТР

5) Вычислить коэффициент цензурирования

1)10/lg(8.055.1 −⋅⋅+=

6) Исключить из выборки все значения (промахи), лежащие за

пределом интервала

σσ

⋅+≤≤⋅− GXxGX

ЦЕНТРЦЕНТР

Если в выборке присутствовали промахи, то ее объем

уменьшился. Обозначим как

Mkx

,...,1},{

очищенную

от промахов выборку

)( NM

≤

. Все дальнейшие операции

будут проводиться с очищенной выборкой.

7) Заново вычислить параметры распределения

∑

−

−−

⋅=

−

)(

)2)(1(

)(

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

)3)(2(

)1)(32(3

)(

)3)(2)(1(

321

−−

−

−−

−−−

+−

⋅=

∑

MMM

8) Рассчитать оптимальное количество столбцов гистограммы

4.0

5.1

Полученное число округлить вниз до ближайшего большего

или равного пяти нечетного целого.

9) Рассчитать левую и правую границы гистограммы

|)max(|

max

min

XxXX

−+=

−−=

10) Рассчитать ширину столбца гистограммы

|)max(|2

minmax

−

11) Рассчитать массив узлов разбиения на оси х

1,...,1

)1(

min

⋅

−+=

diXX

Интервалы между соседними узлами являются интервалами

разбиения.

12) Рассчитать количество случайных величин из выборки

Mkx

,...,1},{ = , которое попадает в каждый из интервалов

разбиения. В результате получится ненормированная

гистограмма распределения или гистограмма частот. Она

задана в виде массива, который обозначим как

Lis

,...,1},{ = .

13) В случае, если есть основания полагать, что плотность

вероятности должна быть симметричной, и в подтверждение

этого, вычисленный на шаге 7 коэффициент асимметрии

незначительно отличается от нуля, то можно провести

расчетное симметрирование гистограммы. Центральный

столбец остается без изменения, а в симметричных

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

относительно него парах столбцов количество отсчетов

усредняется.

14) Вычислить площадь S ненормированной гистограммы. Она

должна быть равна произведению ширины столбца d на

объем выборки M.

15) Нормировать гистограмму путем деления количества

отсчетов в каждом столбце на S. Таким образом на этом

шаге получена гистограмма плотности вероятности:

MdsSsp

iii

,...,1

)/(/

⋅

16) Рассчитать значения интегральной функции распределения в

узлах разбиения

1,...,2

⋅+=

≡

−−

dpFF

iii

Фактически, на этом шаге мы получили функцию

распределения в табличном виде, то есть мы имеем массив

значений случайной величины

}{

X и соответствующий

ему массив значений

1,...,1},{

LiF

6.4. Гистограмма логарифмов относительных изменений ин-

декса РТС.

Рассмотрим временной ряд, состоящий из

последовательных значений цены некоторого актива

TtP

,...,0},{ = . Тогда цену в момент времени Т можно пред-

ставить, как

111

......

−−

Движение цены актива - это случайный процесс, вызванный

действиями большого количества участников рынка. Предполо-

жим, что отношения цен активов в любой момент времени яв-

ляются случайными величинами с одинаковым законом распре-

деления.

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

Тогда по выборке этих случайных величин, которая может

быть получена из ценового ряда, можно определить их закон

распределения.

Но исследовать непосредственно отношение цен представ-

ляется не совсем удобным. Дело в том, что так как цена не мо-

жет упасть ниже нуля, то отношение цен также не может быть

меньше нуля. С другой стороны, цена может сколь угодно силь-

но вырасти, то есть отношение цен может быть неограниченно

большим. Этих качественных рассуждений достаточно, чтобы

понять, что плотность вероятности отношения цен будет иметь

положительную асимметрию. Однако, если мы перейдем к лога-

рифмам отношения цен, ситуация изменится.

)ln(...)ln(...)ln()ln()ln()ln(

111

−−

+++++=−

Распределение логарифмов уже может быть симметрично и

возможна его аппроксимация одним из аналитических законов

распределения, которые были рассмотрены во второй главе.

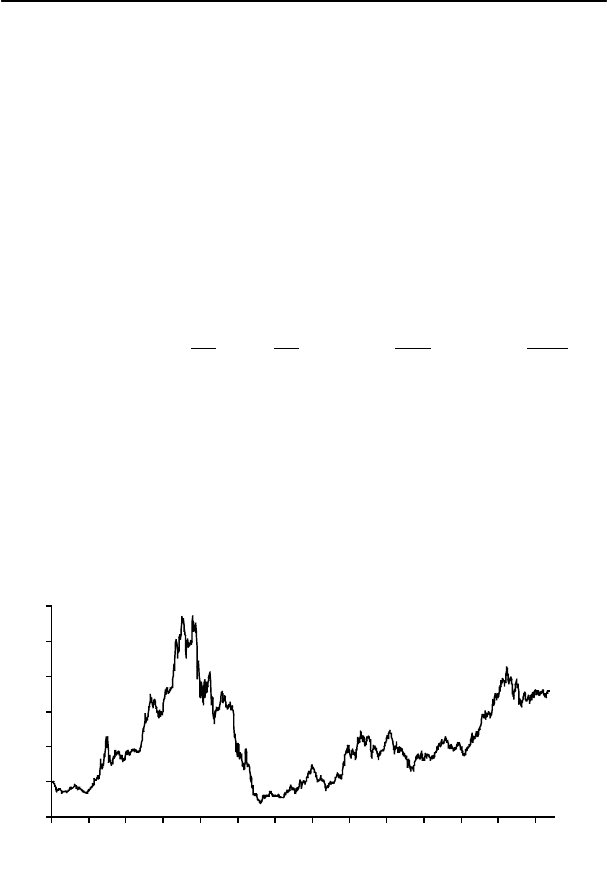
В качестве примера ценового ряда рассмотрим индекс Рос-

сийской торговой системы (индекс РТС) за период с 1 сентября

1995 года по 31 декабря 2002 года. График этого ряда изображен

на рисунке:

Индекс РТС

100

200

300

400

500

600

сен.95

мар.96

окт.96

апр.97

ноя.97

июн.98

дек.98

июл.99

янв.00

авг.00

фев.01

сен.01

апр.02

окт.02

Исследуемой выборкой случайных величин будут нату-

ральные логарифмы отношения цен закрытия индекса РТС.

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

Подробный алгоритм вычисления параметров распределе-

ния, построения графиков плотности распределения и функции

распределения рассмотрен в предыдущем параграфе, поэтому

здесь приведем только результаты.

Наименование оценки Величина

Центр распределения (математическое

ожидание)

0.0007

Среднеквадратичное отклонение 0.0324

Коэффициент асимметрии -0.3064

Эксцесс 7.4301

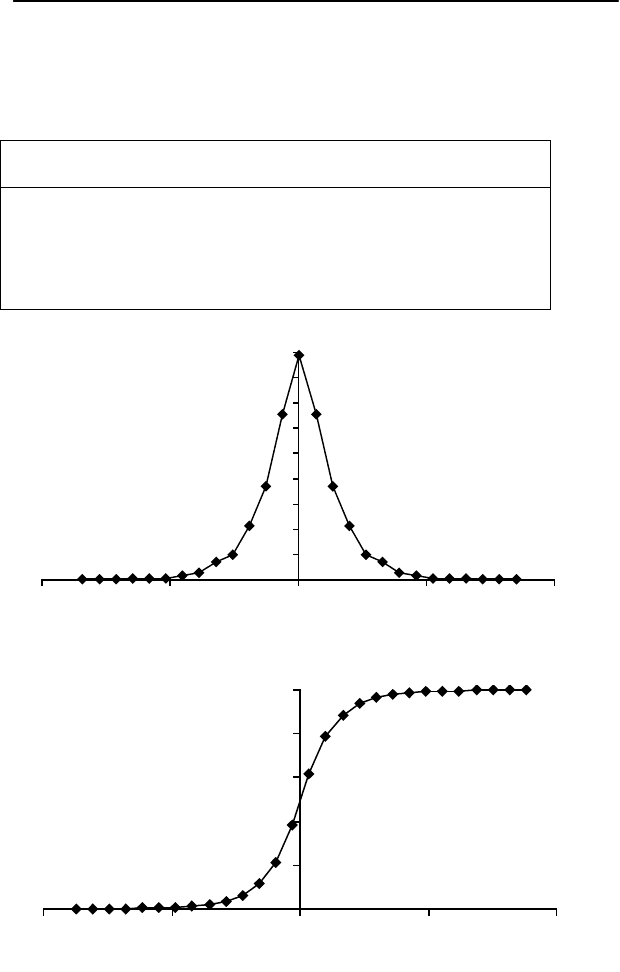
Плотность вероятности

-0.20 -0.10 0.00 0.10 0.20

Функция распределения

0.0

0.2

0.4

0.6

0.8

1.0

-0.20 -0.10 0.00 0.10 0.20

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

Отметим, что с.к.о. превышает математическое ожидание

более чем в 46 раз, то есть исследуемая случайная величина яв-

ляется высоковолатильной. Распределение имеет очень неболь-

шую отрицательную асимметрию, которая вероятно носит слу-

чайный характер, поэтому гистограмма плотности вероятности

была центрирована.

Эксцесс распределения существенно превышает эксцесс

нормального распределения, то есть данное распределение яв-

ляется островершинным.

Гистограмма распределения имеет 27 столбцов. Для боль-

шей наглядности плотность вероятности приведена не в виде

гистограммы, а как плавная линия, проходящая через середины

интервалов разбиения.

6.5. Использование критериев согласия при идентификации

закона распределения случайной величины.

После построения гистограммы распределения можно вы-

двинуть гипотезу о том, что данная гистограмма может быть ап-

проксимирована одним из изученных ранее законов распределе-

ния. При этом степень близости гистограммы и принятой анали-

тической модели может быть проверена с использованием кри-

териев согласия. Здесь будет рассмотрен один из этих критериев

- критерий

Пирсона.

При использовании критерия согласия Пирсона необходимо

вычислить величину:

∑

−

)(

где

L - количество столбцов гистограммы,

s - фактическая частота попадания в i-й столбец,

T - теоретическая частота попадания в i-й столбец.

Для идеально подобранной модели все разности )(

−

равны

нулю и, следовательно, величина

также равна нулю. Таким

образом, ненулевое значение

является мерой суммарного рас-

хождения между фактическим распределением и моделью.

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

Насколько велико это расхождение можно проверить, срав-

нив фактическое значение

с теоретической величиной

q−

которая определяет максимально возможное расхождение меж-

ду фактическими данными и моделью, соответствующее приня-

тому уровню значимости

q .

Уровень значимости q определяет вероятность ошибки 1-го

рода, то есть вероятность того, что будет отвергнута не проти-

воречащая эмпирическим данным модель.

Величина

- это число степеней свободы

распределения. Число степеней свободы зависит от количества

столбцов гистограммы эмпирических данных L и количества

параметров r, описывающих теоретическую модель:

rL −

−

= 1

Величина

q−

- это такая квантиль

-распределения, что

)1(100 q− процентов всех значений случайной величины

лежат слева от

q−

, а q100 процентов всех значений

случайной величины

лежат справа от

q−

Если

χχ

q−

≤ , то считают, что модель не противоречит

фактическим данным при заданном уровне значимости.

Если

χχ

q−

> , то считают, что при заданном уровне

значимости модель не описывает удовлетворительным образом

фактические данные и должна быть отвергнута.

Следует особо подчеркнуть, что при проверке модели по

критерию согласия определенным является лишь отрицатель-

ный ответ, то есть отклонение модели.

Положительный ответ означает лишь то, что модель не про-

тиворечит эмпирическим данным. Это вовсе не означает, что

именно этой моделью данные описываются на самом деле, что

это наилучшая модель, что нельзя подобрать другую модель для

описания данных и т.д. Фактически, положительный ответ при

проверке по критерию согласия следует понимать как "возмож-

но эти данные описываются такой-то моделью", и не более того.

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

Вернемся к полученной в предыдущем параграфе гисто-

грамме натуральных логарифмов относительного изменения це-

ны закрытия индекса РТС.

Гистограмма имеет ярко выраженный пик и достаточно по-

логие спады. Островершинность подтверждается еще и значени-

ем эксцесса, существенно превышающим эксцесс нормального

распределения. Как нам уже известно, распределения с подоб-

ными характеристиками могут быть описаны обобщенным экс-

поненциальным распределением с показателем степени меньше

двух.

Выдвинем гипотезу о том, что фактическое распределение

описывается моделью

+∞<<∞−













−

−= x

λσ

λσα

exp

)/1(2

)(

где

математическое ожидание 0007.0

среднеквадратичное отклонение 0324.0

показатель степени 87.0

Показатель степени был найден из значения оценки эксцес-

са распределения, так как для обобщенного экспоненциального

распределения показатель степени и эксцесс имеют взаимно од-

нозначное соответствие:

)]/3(/[)/5()/1(

αααε

ГГГ=

Исследуемое эмпирическое распределение имеет 27 столб-

цов. Аналитическая модель имеет 3 параметра. Следовательно,

число степеней свободы для критерия Пирсона равно

2331271

−

−=−

−

= rL

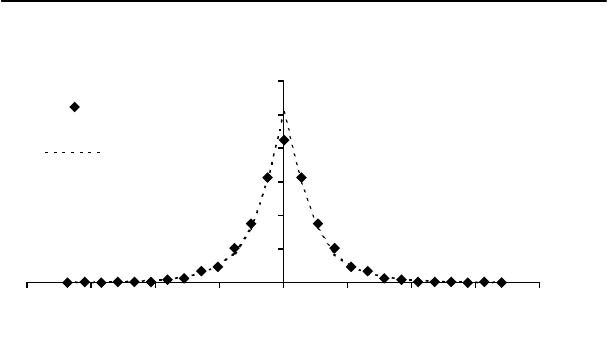
Фактические и теоретические частоты попадания в столбцы

гистограммы дадим для наглядности в графическом виде.

Глава 6. Идентификация закона распределения по выборке случайной ве-

личины

С.В. Булашев. Статистика для трейдеров (электронная версия).

Распределение фактических и теоретических частот

100

200

300

400

500

600

-0.20 -0.15 -0.10 -0.05 0.00 0.05 0.10 0.15 0.20

Фактическая

частота

Теоретическая

частота

Фактическое значение 635.35

. Проверим гипотезу о

том, что

χχ

q−

≤ .

χχ

−

≤

Пусть уровень значимости 01.0

q . Тогда граница крити-

ческой области вычисляется как:

638.41)23,01.0(2

−

ОБРХИ

Так как

χχ

q−

≤ , то исследуемое распределение при

заданном уровне значимости можно аппроксимировать

обобщенным экспоненциальным распределением.

В заключении следует сказать, что для ликвидных

российских акций, торгующихся в РТС, таких как РАО ЕЭС,

Лукойл, Сургутнефтегаз, Ростелеком, Мосэнерго,

распределения логарифмов относительного изменения цены за-

крытия также можно описать обобщенным экспоненциальным

распределением с соответствующим математическим

ожиданием, среднеквадратичным отклонением и показателем

степени.