Булашев С.В. Статистика для трейдеров

Подождите немного. Документ загружается.

Глава 8. Регрессионный анализ

С.В. Булашев. Статистика для трейдеров (электронная версия).

131

- В общем случае считаем, что зависимость между фактором

Х и откликом Y нелинейна. Тогда, используя результаты из

предыдущего параграфа, преобразуем исходную выборку

Nkyx

,...,1),,( = таким образом, чтобы в первом при-

ближении можно было считать, что связь между преобразо-

ванными данными

Nkyx

,...,1),,(

)

носит линейный ха-

рактер.

- Вычисляем параметры линейной регрессии.

- Вычисляем ошибки МНК Nke

,...,1,

- Проверяем свойства ошибок МНК. Если ошибки не удовле-

творяют допущениям МНК, то полученная аппроксимация

является слишком грубой.

- Дальнейшее уточнение модели можно сделать, если в каче-

стве зависимой переменной использовать полученные

ошибки, то есть выборка приобретает вид

Nkex

,...,1),,( =

)

. Эту выборку необходимо обработать по

той же схеме. Процесс продолжается до тех пор, пока на оп-

ределенном шаге ошибки не станут удовлетворять допуще-

ниям МНК. При этом надо помнить, что нельзя излишне пе-

реусложнять модель, и что полученные по модели результа-

ты должны разумным образом интерпретироваться.

Глава 9. Анализ Фурье

С.В. Булашев. Статистика для трейдеров (электронная версия).

132

9. АНАЛИЗ ФУРЬЕ

9.1. Введение.

В этой главе излагается метод аппроксимации эмпириче-

ской зависимости тригонометрическим рядом Фурье. Даны

формулы, позволяющие по реальной выборке вычислить коэф-

фициенты Фурье, амплитуду и фазу гармоник. Рассказано, как

строится амплитудно-частотная характеристика разложения, и

как она используется для выделения гармоник с максимальной

амплитудой.

9.2. Численный анализ Фурье.

Пусть выборка значений фактора Х и отклика Y задана в ви-

де массива

Nnyx

,...,0),,(

, содержащего 1

N точку,

причем все значения фактора Х упорядочены по возрастанию и

равноотстоят друг от друга. Будем считать, что величина Х из-

меняется в интервале

),0(

max

X , следовательно выборка фактора

Х задается рядом

NnXx

max

⋅

Если принято решение о том, что связь переменных Х и Y

носит периодический характер, то аппроксимировать зависи-

мость Y от Х на интервале

),0(

max

X необходимо тригонометри-

ческим рядом, то есть функцией вида:

∑

= 





































maxmax

sin

cos

)(

ππ

Данная функция зависит от (2М+1) параметра

),...,,,...,,(

110 MM

bbaaa . Так как количество неизвестных пара-

метров

12 +

не должно превышать объем выборки 1

N , то

2/NM ≤ .

Наилучшим приближением будет тригонометрический ряд с

таким набором параметров, который минимизирует сумму квадра-

тов отклонений этого ряда от выборочных значений отклика Y, то

есть

∑

→−=

xfyS

min)]([

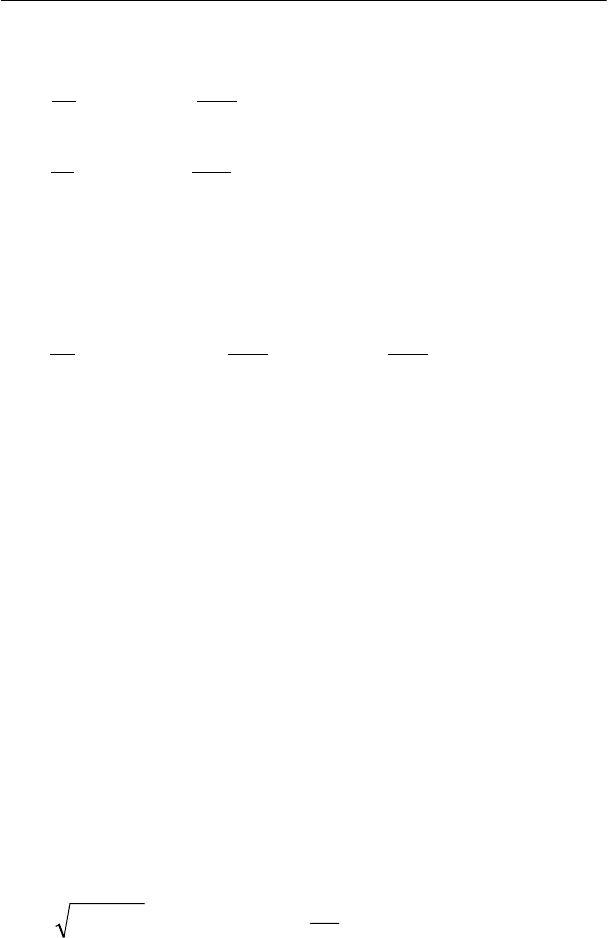
Глава 9. Анализ Фурье

С.В. Булашев. Статистика для трейдеров (электронная версия).

133

Без доказательства приведем формулы для определения

искомых параметров:

≤≤













≤≤













∑

−

sin

cos

Определенные по этим формулам параметры называют

коэффициентами Фурье, а тригонометрический ряд с такими

коэффициентами является рядом Фурье. Тогда аппроксимация

величины Y рядом Фурье в точке

NnXx

max

будет равна:

∑





































mmn

sin

cos

ππ

При увеличении количества гармоник М эта аппроксимация

все точнее описывает выборочные значения величины Y, и

наконец при

2/NM = для любого n становится справедливым

равенство

fy = .

Однако, наша задача состоит не в том, чтобы с абсолютной

точностью аппроксимировать исходную выборку, то есть

включить в математическую модель все наблюдающиеся осо-

бенности конкретной выборки, в том числе и те, которые в дей-

ствительности носят случайный характер. Нам нужно найти все-

го несколько наиболее значимых гармоник, то есть гармоник,

имеющих максимальную амплитуду. Для этого необходимо по-

строить и проанализировать амплитудно-частотную характери-

стику разложения.

9.3. Амплитудно-частотная характеристика.

Введем параметры ),(

, которые назовем амплитуда и

фаза соответственно. Эти величины связаны с параметрами

),(

ba следующими соотношениями:

mmmmmm

mmmm

RbRa

arctgbaR

θθ

πθπθ

sincos

−==

≤<−−=+=

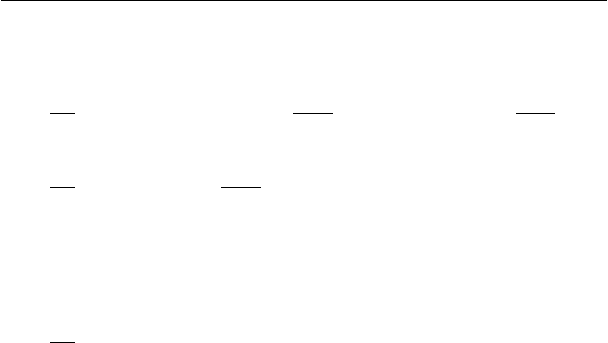
Глава 9. Анализ Фурье

С.В. Булашев. Статистика для трейдеров (электронная версия).

134

Тогда, заменив параметры ),(

ba , разложение Фурье можно

переписать в виде

∑













++=

























−













mmn

mmmmn

cos

sinsin

coscos

Назовем частотой колебаний величину Nm

. Полный

набор частот называется спектром разложения. Тогда оконча-

тельно получаем

()

∑

++=

mmmn

2cos

θπω

Смысл приведенных выше преобразований состоит в том, чтобы

перейти от ряда из синусов и косинусов к ряду из одних косину-

сов. Если теперь построить график, где по оси абсцисс отложена

частота, а по оси ординат отложена амплитуда, то есть график в

координатах

),(

, то наглядно будет видно, при каких зна-

чениях частоты наблюдаются максимумы амплитуды. Такой

график называется амплитудно-частотной характеристикой

(АЧХ). С помощью АЧХ мы получаем возможность выбрать из

разложения Фурье только самые значимые гармоники и пренеб-

речь остальными. Заметим, что период колебания связан с

частотой соотношением

При необходимости аналогичным образом можно построить

фазочастотную характеристику (ФЧХ), то есть график в коор-

динатах

),(

9.4. Пример выделения основной гармоники с помощью

анализа Фурье.

Рассмотрим выделение основной гармоники с помощью

анализа Фурье на примере выборки, состоящей из 256-ти точек

255,...,0),,( =nyx

. График исходных данных приведен на

рисунке.

Глава 9. Анализ Фурье

С.В. Булашев. Статистика для трейдеров (электронная версия).

135

-6

-4

-2

0 50 100 150 200 250 300

Исходные данные

Этот график дает основания предположить, что связь перемен-

ных Х и Y носит периодический характер. По методике, изло-

женной в предыдущих 2-х параграфах, представим аппроксими-

рующую функцию рядом Фурье и построим амплитудно-

частотную характеристику.

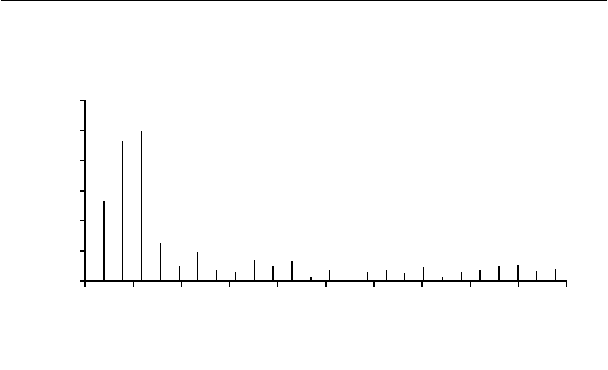
АЧХ

100

150

200

250

300

0 0.1 0.2 0.3 0.4 0.5

частота

амплитуда

Максимум амплитуды находится в начальной части спектра.

Рассмотрим подробнее этот участок.

Глава 9. Анализ Фурье

С.В. Булашев. Статистика для трейдеров (электронная версия).

136

АЧХ

100

150

200

250

300

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1

частота

амплитуда

При ближайшем рассмотрении оказывается, что максимум

амплитуды приходится на частоту

01.0

≈

(период 100

≈

T ).

Учитывая, что

, рассчитаем для этого значения час-

тоты коэффициенты разложения Фурье:

8918.2)(

1049.0)(

−==

Используя эти данные, вычисляем амплитуду и фазу основной

гармоники:

6070.1

8934.2

Таким образом, Фурье-аппроксимация исходных данных и

ошибки модели будут вычисляться по формулам

()

(

)

nnn

mmmn

fye

nnRf

−=

⋅

= 607.101.02cos8934.22cos

πω

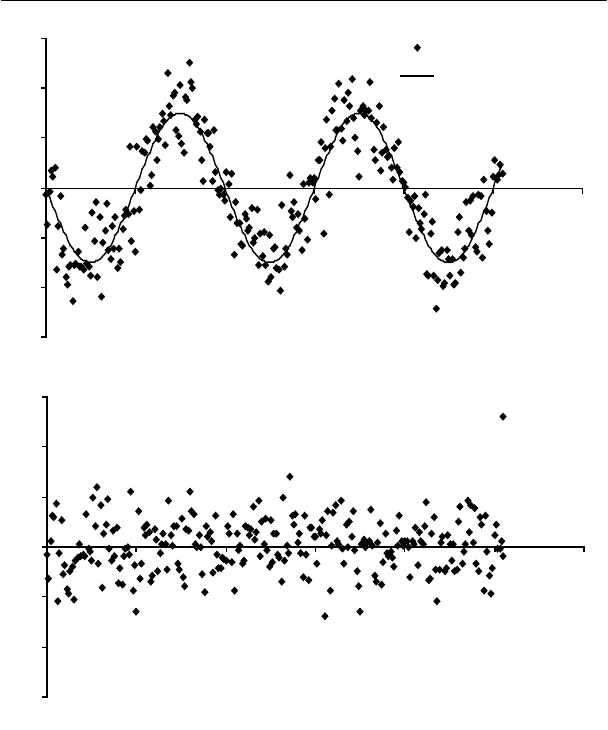
Приведем график исходных данных вместе с Фурье-

аппроксимацией и график остатков (ошибок модели).

Глава 9. Анализ Фурье

С.В. Булашев. Статистика для трейдеров (электронная версия).

137

-6

-4

-2

0 50 100 150 200 250 300

Исходные данные

Фурье-аппроксимация

-6

-4

-2

0 50 100 150 200 250 300

Остатки

Очевидно, что ошибки аппроксимации носят непериодиче-

ский характер. В противном случае нужно было бы повторить

всю процедуру, используя в качестве исходной выборки эти

ошибки, и повторять ее до тех пор, пока не будут выделены все

значимые гармоники.

Па практике, при изучении динамики цен активов не реко-

мендуется использовать для аппроксимации этих рядов более

трех гармоник Фурье.

Глава 10. Применение МНК при изучении динамических рядов

С.В. Булашев. Статистика для трейдеров (электронная версия).

138

10. ПРИМЕНЕНИЕ МНК ПРИ ИЗУЧЕНИИ ДИНАМИ-

ЧЕСКИХ РЯДОВ

10.1. Введение.

Аналитическая аппроксимация динамического временного

ряда, содержащего цены некоторого актива в последовательные

моменты времени, представляет собой математическую модель

развития во времени этого динамического ряда и описывает

присущие ему статистические характеристики.

Аналитическая аппроксимация содержит в себе некоторую

условность, связанную с тем, что цена актива рассматривается

как функция времени. На самом деле цена зависит не от того,

сколько времени прошло с начального момента, а от того, какие

факторы на нее влияли, в каком направлении и с какой интен-

сивностью они действовали. Зависимость от времени можно

рассматривать как внешнее выражение суммарного воздействия

этих факторов. Удовлетворительным образом аппроксимировать

динамический ряд с помощью метода наименьших квадратов

возможно лишь тогда, когда воздействие всех влияющих факто-

ров однородно на всем рассматриваемом промежутке времени.

В случае, если динамический ряд цены актива удается ап-

проксимировать аналитической функцией времени с соблюде-

нием допущений МНК, становится возможной экстраполяция

этой функции, то есть прогноз цены в будущие моменты време-

ни. Однако при этом стоит помнить, что при прогнозе неявным

образом предполагается, что те же самые условия, в которых

формировались цены в прошлом, будут существовать и в буду-

щем. Использование экстраполяции в изменившихся условиях

будет приводить к ошибкам, выходящим за рамки обычных для

МНК погрешностей, связанных с шириной полосы неопреде-

ленности линии регрессии. Долгосрочные прогнозы сопряжены

с большими ошибками, чем краткосрочные. Во-первых, это свя-

зано с расширением полосы неопределенность линии регрессии

при удалении от центра тяжести эмпирических данных, по кото-

рым эта линия была получена. Во-вторых, это связано с возрас-

танием влияния новых факторов при увеличении периода про-

гноза.

Глава 10. Применение МНК при изучении динамических рядов

С.В. Булашев. Статистика для трейдеров (электронная версия).

139

Для того, чтобы динамический ряд можно было эффектив-

ным образом аппроксимировать с применением МНК, этот ряд

должен удовлетворять следующим условиям:

- быть достаточно длинным,

- быть как можно менее волатильным.

При этом следует сказать, что применение МНК при изучении

временных рядов имеет следующие особенности:

- для адаптирования регрессионной модели к изменяющимся

условиям необходимо периодически пересчитывать пара-

метры модели с учетом новых данных, а иногда возможно

пересматривать саму модель,

- при расчете параметров регрессии все эмпирические данные

входят с одинаковым весом, хотя интуитивно понятно, что

более поздние данные имеют большую ценность.

10.2. Модель динамики цен активов.

Биржевые цены активов формируются как результат совме-

стных действий большого количества участников рынка и, как

следствие этого, в них присутствует случайная составляющая.

Рассмотрим временной ряд, состоящий из последователь-

ных значений цены некоторого актива

PPP ,...,,

. Цена не мо-

жет быть отрицательной, но может принимать сколь угодно

большие положительные значения. Следовательно, и отношение

цен в последовательные моменты времени

−kk

PP также не

может оказаться ниже нуля, но может быть сколь угодно боль-

шим. Значит плотность вероятности цен активов и плотность

вероятности отношения цен должны иметь положительную

асимметрию.

Ситуация меняется при переходе к логарифмам отношения

цен, то есть к величине

)/ln(

1−

∆

kkk

PPy . Распределение лога-

рифмов уже может быть симметрично и возможна его аппрок-

симация одним из аналитических законов распределения, кото-

рые были рассмотрены во второй главе (как правило обобщен-

ным экспоненциальным распределением). При этом логарифм

цены в произвольный момент времени складывается из лога-

рифма цены в начальный момент времени (эта величина пред

Глава 10. Применение МНК при изучении динамических рядов

С.В. Булашев. Статистика для трейдеров (электронная версия).

140

полагается нестохастической) и суммы логарифмов отношения

цен:

∑

−

kkt

PPPP

)/ln()ln()ln(

Если величины )/ln(

1−

∆

kkk

PPy независимы и имеют конеч-

ную дисперсию, то согласно центральной предельной теореме

величина

)ln(

Py = будет нормально распределена при любом

законе распределения

∆

. Так как логарифм цены распределен

нормально, то цена подчиняется логнормальному распределе-

нию.

Итак, если все случайные величины

∆

независимы и под-

чиняются одному и тому же закону распределения с математи-

ческим ожиданием

и дисперсией

, то случайная величина

)ln(

P будет иметь нормальное распределение с математиче-

ским ожиданием

и дисперсией t

. Следовательно, лога-

рифм цены в произвольный момент времени можно записать как

zttPP

σµ

++= )ln()ln(

где случайная величина z подчиняется стандартному нормаль-

ному распределению.

Рисковые активы имеют положительное математическое

ожидание дохода, следовательно

. Величина

определя-

ет тренд актива, то есть воздействие на цену постоянно дейст-

вующих систематических факторов.

Величина

определяет волатильность актива, то есть воз-

действие на цену множества случайных факторов.

Отношение ожидаемого дохода к ожидаемому риску за еди-

ницу времени

/ характеризует степень устойчивости роста

цены актива. Чем выше это отношение, тем привлекательнее

при прочих равных условиях инвестиции в данный актив.

Наряду с влиянием постоянно действующих факторов и

случайных колебаний, цена актива может испытывать воздейст-

вие причин, характеризующихся циклическими колебаниями.

Возникновение циклов связано с изменением оценки инвесто