Braun J., van der Beek P., Batt G. Quantitative Thermochronology: Numerical Methods for the Interpretation of Thermochronological Data

Подождите немного. Документ загружается.

68 The general heat-transport equation

4.8 Purely conductive heat transport

As stated earlier, our main purpose in using thermochronology is to constrain the

rate at which rocks are exhumed towards the surface of the Earth and, potentially,

to estimate the rate at which landforms (the shape of the surface) evolve. As we

will see in the next chapters, the advection of rocks towards the surface may

lead to a noticeable perturbation of the temperature structure within the crust; but

before we investigate this, we must define the ‘reference’, undisturbed, conductive

solution whereby the crustal temperature is determined by the one-dimensional

balance between heat flowing upwards by conduction from the underlying mantle

and heat lost into the overlying atmosphere. This is a rather simple problem that

is complicated only by the presence of heat-producing elements such as uranium,

thorium and potassium in the crust and the variability of the thermal conductivity

of crustal rocks. This simple solution can also be used to determine the thermal

history of rocks being exhumed in regions of low tectonic activity, typically where

exhumation is driven by isostatic rebound associated with surface erosion.

Conductive equilibrium – uniform conductivity – no heat production

The simplest form of the heat-transfer equation assumes steady state (T/t =0),

a purely conductive heat transport in the vertical dimension, a fixed surface

temperature, Tz = 0 = T

, and, at the base of the crust, a fixed heat flux from

the mantle

T

z

z = L =q

In this situation, the general heat-transfer equation (4.15) becomes



z

= 0 (4.18)

which, after integration, can be further reduced to

T

z

= q

(4.19)

Integrating (4.19) leads to a simple linear increase of temperature with depth:

Tz = T

z (4.20)

Thus, in a tectonically quiet region where rocks have a low content of radio-

genic heat-producing elements and where conductivity (which we will assume

is constant within, and can therefore be read as a proxy for, a given lithology)

is uniform, the temperature increases linearly with depth. Typical mantle heat-

flow values are in the range 10–30 mW m

−2

; a commonly accepted value for

4.8 Purely conductive heat transport 69

the mean crustal conductivity is 3Wm

−1

(Turcotte and Schubert, 1982).

The rate of increase of temperature with depth should therefore be in the range

3–10



Ckm

−1

. In most regions of the Earth, however, the geothermal gradi-

ent is significantly higher, typically of the order of 15–20



Ckm

−1

(Turcotte

and Schubert, 1982). This is due to the contribution to the heat balance from

heat-producing elements (see Section 4.8).

In a region where exhumation is very slow (typically <01mm yr

−1

), conduc-

tion dominates heat transport. Assuming that the contribution from heat-producing

elements can be neglected, the conductive temperature distribution given by (4.20)

is a good approximation that can be used to determine the exhumation rate,

from thermochronological data. If t

is the age of a rock for a thermochronometric

system characterised by a closure temperature T

, one can write

= T

(4.21)

or, assuming a zero surface temperature,

E =

(4.22)

where G is the conductive geothermal gradient, G = q

/k.

Equation (4.22) shows that, to determine the exhumation rate under the assump-

tion of conductive equilibrium, one needs to know the mantle heat flow which,

in this case, is equivalent to the local surface geothermal gradient divided by the

conductivity of the rock. This is true even in the case when two or more ages

(i.e. time–temperature pairs) are known.

Conductive equilibrium – variable conductivity

As shown in Table 4.1, the thermal conductivity of rocks is highly variable. From

Equation (4.15), it is clear that spatial variations in thermal conductivity will lead

to spatial variability in temperature. We will now show that, even in situations

where the Earth’s crust could be assumed to be laterally homogeneous and to

have reached conductive equilibrium, vertical variations in thermal conductivity

lead to changes in vertical temperature gradient.

For a material in which thermal conductivity varies with depth, the equation of

conductive thermal equilibrium can be written as



z

kz

T

z

= 0 (4.23)

Under the assumption that the crust is made of a series of horizontal layers, each

characterised by a different conductivity, at equilibrium, the temperature must

increase linearly within each layer. The geotherm is thus made of a series of linear

70 The general heat-transport equation

Table 4.1. Thermal conductivity for a range of rock types; data from

Clauser and Huenges (1995)

Rock type Conductivity (W m

−1

)

Sedimentary rocks 0.5–4.5 (inversely ∝ porosity)

Volcanic rocks 1.5–3.5 (inversely ∝ porosity)

Metamorphic rocks (low quartz content) 1–4

Metamorphic rocks (high quartz content) 5–7

segments of varying slope, inversely proportional to the thermal conductivity,

such that the heat flow through each layer, q

= q

, is uniform with depth and

equal to the product of the conductivity of the layer, k

, and the local geothermal

gradient:

=−k

T

z

(4.24)

Regions where rocks have a low thermal conductivity (such as in sedimentary

basins) are characterised by a high geothermal gradient, whereas regions where

rocks have a high thermal conductivity (such as in high-grade metamorphic ter-

ranes) are characterised by a relatively low geothermal gradient.

The exact form of the temperature distribution can be written as

Tz = A

z −d

for d

<z<d

i+1

= d

(4.25)

where l

is the thickness of layer i and d

the depth to the top of layer i. The

value of the 2N constants A

and B

can be derived from the assumed temperature

boundary condition at the surface,

Tz = 0 = T

(4.26)

the imposed mantle heat flux at the base,

T

z



z=d

= q

(4.27)

and the continuity of temperature and conservation of energy (continuity of heat

flux) along interfaces between each pair of layers.

The surface and bottom boundary conditions give us

= T

(4.28)

4.8 Purely conductive heat transport 71

while continuity of temperature leads to

= B

i+1

for i = 1N −1 (4.29)

and continuity of heat flux to

i+1

for i = 1N −1 (4.30)

Combining these relationships leads to the following expressions for the A

and B

= q

i−1



j=1

(4.31)

If we now assume that rocks are being exhumed at a low but constant rate

through such a thermal structure, they will experience several periods of uniform

cooling, corresponding to the exhumation of each layer, as shown in Figure 4.5.

Naïve application of Equation (4.22), in the absence of constraints on regional

thermal-conductivity variations, may lead to the interpretation of rapid (and wholly

artefactual) changes in exhumation rate having occurred. It is therefore important

to take into account any knowledge one may have as to the conductivity struc-

ture of the crust during exhumation in the interpretation of thermochronological

data.

In general, most sediment types are characterised by a relatively low conduc-

tivity such that sedimentary basins are usually characterised by a high geothermal

gradient; this is called the ‘blanketing effect’ of the sediments on the under-

lying crust (see Sandiford (1999) for an interesting discussion of the effect of

the sedimentary cover on the thermal structure of the crust and its rheological

implications).

time

Fig. 4.5. The thermal history of a rock particle exhumed within a vertically

layered conductivity structure.

72 The general heat-transport equation

Table 4.2. Heat production for a range of rock

types; data from Förster and Förster (2000)

Rock type Heat production (Wm

−3

)

Sedimentary rocks 0.5–5.5

Granitic rocks 2.5–3.5

(varies with differentiation)

Metamorphic rocks 1.5–3.5

In a study of the denudation history of the southeastern Brazilian margin,

Gallagher et al. (1994) showed how failure to take the nature of the overburden

removed by denudation (in their case, low-conductivity volcanics) into account

may lead to erroneous estimates of the depth of denudation from apatite fission-

track (FT) data.

Conductive equilibrium – the effect of heat production

Plate-tectonic behaviour can be viewed as a response to heat transport in a

thermally stratified system. Heat produced by radioactive isotopes keeps the

interior of the Earth hot enough to drive convective overturn of the mantle,

producing movement in the overlying coupled lithospheric plates. Many of these

elements exist in the mantle but at relatively low concentrations. During the

formation and differentiation of the Earth and the subsequent formation of the

continental crust by magmatic processes, these elements became concentrated in

the continental crust. The presence of radioactive elements and the heat they

produce perturb the conductive thermal gradient.

Typical values of the heat produced by various rocks are given in Table 4.2.

Heat-producing elements are most concentrated in granitic rocks and the sediments

derived from them.

The one-dimensional steady-state conductive-heat-transport equation including

the effect of heat production is



z

+H =0 (4.32)

Assuming a uniform distribution of radioactive elements in the crust, the general

solution of this equation is a second-order polynomial (or quadratic function):

T =a

z +a

(4.33)

4.8 Purely conductive heat transport 73

By introducing this solution into the differential equation, one can easily show

that

=−

H

(4.34)

Assuming that the surface temperature is fixed, Tz =0 =T

, and that a constant

(mantle) heat flux, q

, is imposed at the base of the crust, i.e. at z = L, one can

easily find the values of the two other constants, a

and a

= T

HL

(4.35)

such that the temperature distribution within the crust is given by

Tz =−

H



HL



z +T

(4.36)

This expression can be used to derive the temperature history, Tt, of a rock

particle being exhumed at a constant and slow rate,

Tt =−

H



Et



HL



Et +T

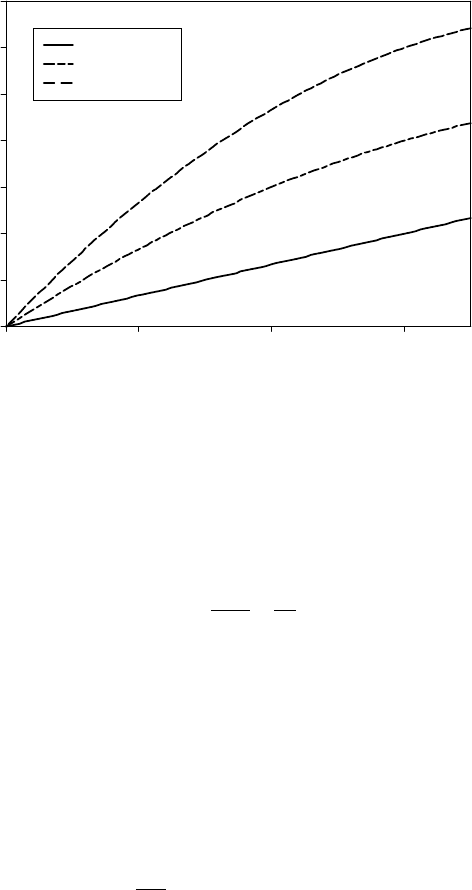
(4.37)

One can readily see that the thermal history of a rock particle being exhumed in

a region characterised by a finite and uniform concentration of heat-producing

elements is quadratic in time (i.e. it varies as the square of time), predicting an

accelerated cooling in the recent past and thus an apparent increase in exhumation

rate if temperature is wrongly interpreted as a simple, linear proxy for depth (see

Figure 4.6).

If we have at least two independent age–temperature constraints (corresponding

to two different thermochronological systems), we can derive the values of the

two coefficients in Equation (4.37),

H

and



HL



E (4.38)

assuming that we know the surface temperature, T

. We can then extract the

value of the exhumation rate,

E, by assuming that we know either the mantle

component of the heat flow, q

, or the mean heat-production rate, H.

Note that because heat-producing elements are mostly concentrated in the upper

crust, one commonly assumes that heat production is limited to a layer in the

uppermost part of the crust of thickness l. In this case, the temperature distribution

in the crust is made of two separate domains: the top one (i.e. from z =0toz =l)

is characterised by a quadratic increase of temperature with depth given by

Tz =−

H



Hl



z +T

(4.39)

74 The general heat-transport equation

Time (Myr)

0 100 200 300

Temperature (°C)

100

200

300

400

500

600

700

ρH =0

ρH =1 mWm

–3

ρH =2 mWm

–3

Fig. 4.6. Predicted thermal histories for a rock particle experiencing exhuma-

tion at a rate of 100 m Myr

−1

for a period of 350 Myr. The conductivity

is 3 W m

−1

, the crustal thickness is 35 km and the mantle heat flux is

20 mW m

−2

. The three curves correspond to different values for the assumed

heat production.

and the bottom one is characterised by a linear increase of temperature with depth

at a rate that is given by the ratio of the mantle heat flux and the conductivity:

Tz = T

Hl

z (4.40)

Note that, at z =l, the two solutions lead to the same expression for the temperature

T =T

+Hl

/2k +q

l/k and heat flux q = k T/z = q

.

A similar expression can be derived in situations where the layer of assumed

uniform heat production of thickness l is buried at a depth h beneath the surface

(see Appendix 3).

Another common assumption is that the concentration of heat-producing

elements in the crust decays exponentially with depth. In this case the one-

dimensional, steady-state heat equation becomes:



z

+H

−z/z

= 0 (4.41)

where H

is the rate of heat production at the surface and z

is the depth over

which this rate of production decreases by a factor e. Assuming a constant surface

4.8 Purely conductive heat transport 75

Table 4.3. Surface heat-flow and heat-production

measurements from South Australia

(from Neumann et al. (2000))

Heat flow mW m

−2

 Heat production Wm

−3



48 2.7

71 3.1

76 3.8

57 4.9

109 7.4

127 7.9

92 8.2

temperature and a constant mantle heat flux at the base of the crust (i.e. at z =L),

one can show that the solution to that equation is (Turcotte and Schubert, 1982)

Tz = T



−

H

−L/z



z −

H



−z/z

−1



(4.42)

Tutorial 3

(a) Use the dataset shown in Table 4.3 to derive the mantle component to surface

heat flow in this area of South Australia. (b) Assuming that the heat-producing

elements are uniformly distributed in a thin layer located in the uppermost crust,

what is the thickness of this layer? (c) Predict the one-dimensional thermal struc-

ture in this region of the Earth’s crust and (d) derive the thermal history of a rock

being exhumed at a rate of

E = 01kmMyr

−1

assuming that exhumation has no

effect on the distribution of heat-producing elements. Hint: use the relationship

+HL, relating the surface heat flux, q

, to the mantle heat flux, q

, the

heat-production rate, H, and the thickness of the heat-producing layer, L.

Thermal effects of exhumation

In our quest to extract information on exhumation from thermochrono-

logical data, we now turn our attention to the effects that exhumation

itself, i.e. the advection of rocks towards the Earth’s surface, may have

on the temperature structure of the crust. It is important to realise that

the process that we are trying to quantify, namely rock exhumation, is

strongly non-linear: it perturbs the system that we propose to use to

measure it, i.e. the temperature history of the rock.

5.1 Steady-state solution

We first provide a means of determining the perturbation caused by advection

under the assumption of steady-state exhumation, i.e. for situations in which rock

uplift is balanced by erosion over a long period of time. Although this is an

idealised scenario, it is worth considering, in order to assess the magnitude of

the perturbation and the conditions under which it is likely to be significant.

Furthermore, thermal steady state is not an unlikely scenario when considered on

the scale of an entire, mature orogen, such as in the Southern Alps of New Zealand

or in the Taiwan orogen (Willett and Brandon, 2002).

Uplift and exhumation

As already mentioned in Section 1.2, it is very important always to keep in mind

that the cooling that is documented by thermochronology during exhumation is

related to the advection of rocks towards the cold upper surface of the Earth. Our

ability to derive geological constraints from thermochronology is limited to a spa-

tial window between a sample’s location at the time of sampling and a depth range

corresponding to a temperature range centred around the closure temperature of

5.1 Steady-state solution 77

Past Present

Fig. 5.1. U is rock uplift, i.e. the vertical movement of rocks with respect to the

centre of the Earth; U

is surface uplift, i.e. the vertical movement of the surface

of the Earth with respect to the centre of the Earth; E is exhumation, i.e. the

movement of rocks relative to the surface of the Earth. E = U −U

(see also

Figure 1.6 for a more detailed description of these important concepts).

the relevant system, i.e. comprised between the first retention (or “open-system”)

and blocking temperatures. As illustrated in Figure 5.1, thermochronology pro-

vides information on rock exhumation only; it does not provide constraints on

either rock or surface uplift (England and Molnar, 1990; Brown, 1991).

Note also that, because the surface of the Earth is relatively planar, the horizontal

components of the temperature gradient are much smaller than the vertical one.

In most situations, horizontal tectonic movements do not result in measurable

changes in temperature and, therefore, thermochronology cannot be used directly

to constrain horizontal rock movement. We will discuss the consequences of

exceptions to this rule in Chapter 10.

In this chapter, we will therefore focus on the one-dimensional, vertical-

advection case; in Chapters 6 and 7 we will consider the two- and three-

dimensional cases, respectively.

Basic PDE: the steady-state case

The simplest way to interpret thermochronological data is to assume that an

equilibrium between tectonic rock uplift and erosion has been reached, which

leads to a constant exhumation rate,

E. If this situation is maintained for a long

period of time, a thermal steady state develops, which is governed by a balance

between advection and conduction (Willett and Brandon, 2002). In this situation,

the temperature, T , within the crust does not change with time and is governed

by the following simplified form of Equation (4.15):

−

T

z

= 



z

(5.1)