Braun J., van der Beek P., Batt G. Quantitative Thermochronology: Numerical Methods for the Interpretation of Thermochronological Data
Подождите немного. Документ загружается.


58 Thermochronological systems
Table 3.5. Parameters for commonly used annealing models. For the apatite
models, parameters refer to Equations (3.18) and (3.16) except for the
curvilinear fit of Ketcham et al. (1999), which refers to Equation (3.17). For the
zircon models, parameters refer to Equation (3.21).
Model Composition ab C
0
C
1
C
2
C
3
Laslett (1987) Durango apatite 035 27 −487 0000168 28095 0
Crowley et al.
(1991)
Durango apatite 049 30 −3202 00000937 2567 00004200
Crowley et al.
(1991)
Fluor-apatite 076 416 −1508 000002076 8581 00009967
Ketcham et al.
(1999)
Apatite
(fanning)
015 876 −11053 00003896 17842 00006767
Ketcham et al.
(1999)
Apatite
(curvilinear)
020 742 −26039 05317 62319 −78935
Tagami et al.
(1998)
-Damaged
zircon
1141 00002472 001125
Rahn et al.
(2004)
Zero-damage
zircon
1157 00002755 001075
Durango apatite and fluor-apatite Cl/Cl +F = 002 and Ketcham et al.
(1999) for a range of apatite compositions. Values for the parameters in
Equations (3.16)–(3.18) fitted to these experimental data are given in Table 3.5.
In the multi-compositional model of Ketcham et al. (1999), the actual track-
length shortening for any apatite composition is related to that of the most resistant
apatite in their study by
r
lr
=
r
mr
−r
mr
0
1−r
mr
0
k
(3.20)
where r
lr
and r
mr
are the reduced lengths of the less-resistant and more-resistant
apatites, respectively, and r
mr
0
is the reduced length of the most resistant apatite
at the point where the less-resistant apatite becomes totally annealed. Ketcham
et al. (1999) provided a calibration of the fitting parameters r
mr
0
and k with some
of the most common measures of apatite composition, such as Cl
−
content and
etch-pit width.
Fewer experiments have been conducted on zircon, due to the much longer time
required to produce equivalent degrees of annealing in this mineral (see Rahn
et al. (2004) for a review); models of the form (3.15) and (3.16) have been fitted
to these data (Yamada et al., 1995; Galbraith and Laslett, 1997; Tagami et al.,
1998; Rahn et al., 2004). In Table 3.5 we reproduce the parameter fits from the
3.3 Fission-track thermochronology 59
last two of these studies, for -damaged and zero-damage zircons, respectively.
They have been fitted to a simplified annealing equation:
ln1 −r = C
0
+C
1
T ln t +C
2
T (3.21)
MadTrax.f
The subroutine MadTrax.f models the response of fission tracks to an arbitrary
input thermal history. This is provided by the user in the form of a series of
temperature–time pairs, and the subroutine calculates the annealing experienced by
tracks formed throughout the sample’s history, integrating the results to produce
a synthetic fission-track age and length distribution. The forward model used in
this subroutine is described in detail in Appendix 1.
MadTrax.f is based on the annealing models proposed by Laslett et al. (1987)
and Crowley et al. (1991); the user determines what model parameters to use. A
user-friendly forward and inverse model of fission-track annealing, based on the
‘multi-kinetic’ model of Ketcham et al. (1999), is provided by the code AFTSolve.
An academic, non-commercial version of this code, developed by Ketcham et al.
(2000), is available by downloading from http://www.apatite.com/AFTSolve.html.
Tutorial 2
Use the codes Muscovite.f90 and MadTrax.f to predict muscovite
40
Ar/
39
Ar ages
and apatite fission-track ages and length distributions, respectively, for the five
time–Temperature histories enumerated in Tutorial 1 (Chapter 2). Compare these
with the (U–Th)/He ages predicted previously. What do you deduce from these
comparisons, in terms of the discriminating power of (combinations of) different
thermochronometers?
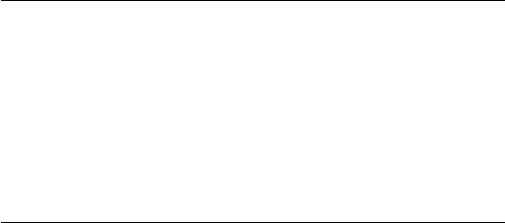
4
The general heat-transport equation
In this chapter, we derive the differential equation governing the trans-
port of heat in solids. This equation is used to estimate the contributions
from conduction, tectonic advection and radiogenic heat production
in geological systems. We discuss the various types of boundary con-
ditions that are applicable in the context of tectonic and geomorphic
problems. We then provide the solution of the heat-transport equation
under the assumption of one-dimensionality and neglecting the effect
of rock advection towards the cold surface. In doing so we provide a
reference conductive solution under a range of assumptions concerning
the conductivity and the rate of heat production in the crust.
4.1 Heat transport within the Earth
In solids, heat is principally transported by conduction or advection. Conduction
implies a transfer of molecular vibrational energy; advection implies a spatial
reorganisation of the internal heat of the system by the relative translation of some
of its parts.
Within the Earth, heat is constantly being produced by the natural radioactive
decay of unstable isotopes, principally uranium, potassium and thorium. The heat
is produced at such a rate and over such a large volume (the entire crust and
mantle) that, if it were transported out of the system by conduction only, the
entire planet would rapidly reach melting temperature. In fact, the transport is
mostly by advection: most of the Earth’s mantle is at such a temperature that it
is sufficiently weak to flow over geological timescales. Following Archimedes’
principle, the hotter, thus less dense, parts of the Earth’s interior tend to rise
towards the surface; in doing so they transport heat by advection. This buoyancy-
driven advection is called convection. As rocks move towards the cold surface,
they cool, becoming more rigid, and conduction progressively takes over as the
60
4.2 Conservation of energy 61
Advection-
dominated
Conduction
-
dominated
Lithosphere
Convecting
mantle
Orogenic system
Balance
between
conduction &
advection
Fig. 4.1. Modes of heat transport in the Earth. In the convecting mantle, advec-
tion dominates, whereas within the lithosphere, which can be regarded as a
thermal boundary layer, conduction dominates, except in active tectonic areas
(orogenic systems), where both conduction and advection operate. Note that the
thickness of the lithosphere (≈100km) has greatly been exaggerated compared
with the mantle thickness (2900 km).
dominant heat-transport mechanism. The relatively thin region over which this
conductive transfer takes place is called the lithosphere.
Being at the interface between the hot, solid Earth and the relatively cold
overlying atmosphere/hydrosphere, the lithosphere is the coldest part of the Earth
system and thus the strongest. This outer shell is composed of a series of discrete,
almost rigid plates that are in relative horizontal motion with respect to each
other. These relative motions are driven by the underlying large-scale convec-
tive flow and may cause the plates to deform, especially along their edges. For
example, where two plates collide, they are subjected to compressional forces,
which, locally, may lead to thickening and uplift of the surface (Figure 4.1). The
topographic gradient induced by the localised uplift causes erosion, transport and
deposition of rocks, which, in turn, may cause transport of heat by advection.
Thus, within the conducting lithosphere, the transport of heat may become locally
dominated by advection.
4.2 Conservation of energy
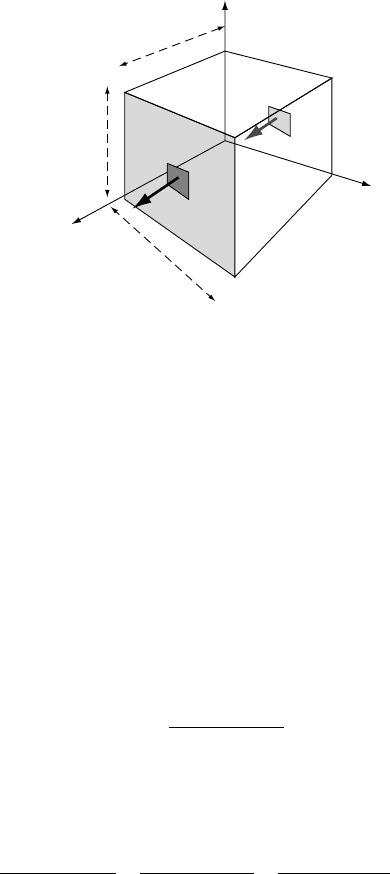
Let’s consider the heat balance within an infinitesimal volume of material as
shown in Figure 4.2. At each point of space, we can define the flux of heat per
unit area and unit time, q = q
x
q
y
q
z
. The amount of heat entering the system
per unit time through one side of the volume is thus given by the product of the
component of the heat flux perpendicular to that side and its surface area. If we
62 The general heat-transport equation
x
y
z
dy
dz
dx
–q
x
(dx)
q
x
(0)
Fig. 4.2. Heat balance in the x-direction. The difference between the heat flux
entering the infinitesimal volume of size dx ×dy ×dz and that leaving the volume
must be compensated by an increase in temperature.
consider one of the two faces perpendicular to the x-axis, we can thus write that
the heat entering the system through that face per unit time is given by
Q
x
= q
x
dy dz (4.1)
The net amount of heat, Q
x
, entering the small volume per unit time in the
x-direction is given by the difference between the heat entering and the heat
leaving through each of the two faces perpendicular to the x-axis:
Q
x
=−Q
x
dx +Q
x
0
=−
q
x
dx −q0
dy dz
=−
q
x
dx −q
x
0
dx
dx dy dz (4.2)
Adding the contributions from each of the other two directions leads to
Q =+Q
x
+Q
y
+Q
z
=−
q
x
dx −q
x
0
dx
+
q
y
dy −q
y
0
dy
+
q
z
dz −q
z
0
dz
dx dy dz (4.3)
The heat capacity, c, of a given system is defined as the amount of heat that
must be given to a unit mass of the system to increase its temperature by one unit

4.3 Conduction 63
of temperature over a unit of time. By virtue of conservation of energy, we can
write
c
dT
dt
dx dy dz = Q (4.4)
where is the density of the material, and thus
c
dT
dt
=−
q
x
dx −q
x
0
dx
+
q
y
dy −q
y
0
dy
+
q
z
dz −q
z
0
dz
(4.5)
We can express the conservation of energy at each point of the system by
collapsing the sides of the small infinitesimal volume to zero, i.e. by calculating
the limit of the right-hand side of (4.5) for dx,dy and dz → 0, which leads to
c
dT
dt
=−
q
x
dx
−
q
y
dy
−
q
z
dz
=−
−→
div ·q (4.6)
where
−→
div ·q is the divergence of the heat flux, that is the sum of the partial
derivatives of the components of the flux. We can thus state that, at any point of
the system, the rate of change of temperature is proportional to the divergence of
the heat flux.
4.3 Conduction
The conduction of heat obeys Fourier’s law, which states that the conductive heat
flux per unit area, q, is proportional to the local temperature gradient,
−→
grad T =
T/x T/y T/z. The constant of proportionality is called the conductivity
of the material, k. Heat always propagates from warm to cold regions; thus the
flux of heat must be in the direction opposite to that of the temperature gradient.
This leads to the following form of Fourier’s law for heat conduction:
q =−k
−→
grad T (4.7)
Introducing this expression into (4.6) leads to the following partial differential
equation governing the transient transport of heat by conduction:
c
dT
dt
=
−→
div ·k
−→
grad T (4.8)
In cases in which the conductivity does not vary spatially, Equation (4.8)
becomes
c
dT
dt
= k
2
T (4.9)
64 The general heat-transport equation
where
2
T =
2
T
x
2
+
2
T
y
2
+
2
T
z
2
(4.10)
is called the Laplacian operator.
Consequently, the basic equation governing transient conductive heat transport
takes the general form of a diffusion equation, i.e. the local rate of change of
temperature is proportional to the second spatial derivative or ‘curvature’ of the
temperature field.
4.4 Advection
In the above basic equation (4.10), the spatial coordinates x y z are attached
to the small volume of rock for which the heat balance is derived. This frame of
reference is somewhat unconventional in Earth-science problems, with the system
of reference more commonly being attached to a particular point in space – the
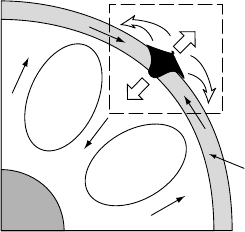
centre of the Earth, or some arbitrary location on the Earth’s surface (Figure 4.3).
Material points (rocks) may move with respect to this system of reference, for
(a)
(b)
Fig. 4.3. Two basic reference systems used to describe heat transport in deform-
ing systems: (a) the Eulerian system of reference, in which the observer (i.e. the
spatial coordinates) is fixed in space and considers the change in temperature in
an infinitesimally small volume through which rock is advected at a known rate
determined by the velocity field [v
x
v
y
v
z
]; and (b) the Lagrangian system of
reference, in which the observer is attached to the moving/deforming system.

4.5 Production 65
example by convective motion in the mantle or by erosion and exhumation in
the crust. If we wish to use spatial rather than material coordinates, we need to
modify the basic conductive-heat-transport equation.
At a given location x y z, the rate of change of temperature is not just equal
to the local rate of change of temperature in the material (the rocks); we must also
consider the fact that rocks are advected at a velocity v and that there might exist a
temperature gradient in the material in that direction. In this case the temperature
at location x y z will change at a rate that is equal to the product of the velocity
and the temperature gradient, such that the total rate of change of temperature is
given by
dT
dt
=
T
t
+v
x
T
x
+v
y
T
y
+v
z
T
z
=
T
t
+v ·
−→
grad T (4.11)
One may also state that, in an Eulerian description of heat transport, i.e. where
spatial coordinates are fixed, space and time cannot be considered as independent
variables; consequently, the rate of change of temperature is equal to the total
derivative of temperature with respect to time and we must write
dT
dt
=
T
t
+
T
x
x
t
+
T
y
y
t
+
T
z
z
t
=
T
t
+v
x
T
x
+v
y
T
y
+v
z
T
z
=
T
t
+v ·
−→
grad T (4.12)
On combining this result with Equation (4.10), we obtain the general transient
heat-transport equation for conduction and advection:
c
T
t
+v ·
−→
grad T
= k
2
T (4.13)
4.5 Production
In the Earth, most rocks contain a finite concentration of radioactive isotopes.
In terms of their overall contribution of heat to the crust and mantle, the most
important of these are isotopes of U, Th and K. The decay of these radioactive
atoms into their daughter products is accompanied by an infinitesimal loss in mass,
which must be compensated by an increased kinetic energy of the newly created
particles and, potentially, by a radiative energy flux. This additional energy must
be taken into account in the global heat budget.
If we define H as the rate of radiogenic heat production per unit mass, the
rate of heat produced by unit volume is H. Adding this term to the heat-balance
equation leads to
c
T
t
+v ·
−→
grad T
= k
2
T +H (4.14)

66 The general heat-transport equation
4.6 The general heat-transport equation
In its explicit form, the general heat-transport/balance equation in the solid Earth
can thus be written as
c
T
t
+v
x
T
x
+v
y
T
y
+v
z
T
z
=
x
k
T
x
+
y
k
T
y
+
z
k
T
z
+H (4.15)
where T is the temperature, t is time, x y and z are the three spatial coordinates
and v
x
v
y
and v
z
are the corresponding components of rock velocity (in a very
general way, defined with respect to the centre of the Earth, or, in a more practical
way, with respect to the surface of the Earth), k is the thermal conductivity, is
the density, c is the heat capacity and H is the rate of radioactive heat production
per unit volume. Further details on the derivation of this equation may be found
in Carslaw and Jaeger (1959) or Turcotte and Schubert (1982).
4.7 Boundary conditions
To understand the thermal structure of the Earth’s crust and its evolution through
time, one must find a solution to this equation or, most probably, one of its
simplified forms that also conforms to a set of boundary conditions and, in the
transient case, to an initial temperature distribution. Boundary conditions are
essentially of two types; they correspond to either a fixed temperature (Dirichlet-
type boundary condition),
T =T
S
(4.16)
which is usually imposed at the surface or at the base of the crust, or a fixed con-
ductive heat flux, in a direction normal to the boundary (Neumann-type boundary
condition),
k
T
z
= q
m
(4.17)
which is usually applied at the base of the crust and/or along the vertical side
boundaries of the region of interest. Note that, for practical reasons, we will
now assume that the z-axis is positive downwards (as shown in Figure 4.4), and
thus vertical heat flux will usually be positive. This is because the temperature
usually increases with depth; temperature gradients are thus positive and so are
conductive heat fluxes. Other types of boundary conditions could be considered
(radiative and convective for instance) but are not covered here.
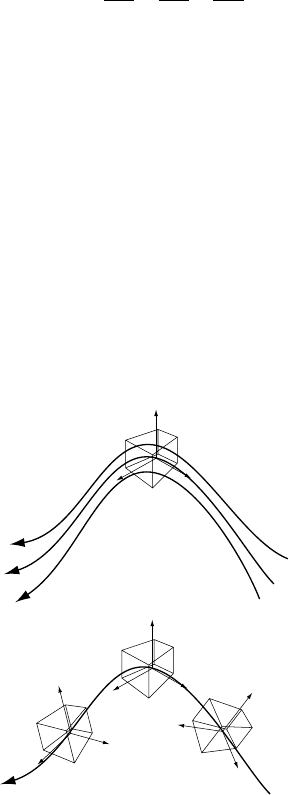
As an example, we show in Figure 4.4 the boundary conditions commonly
used in crustal-tectonics problems: fixed temperature along the free surface, fixed
heat flux along the base, representing the heat loss by conduction from the
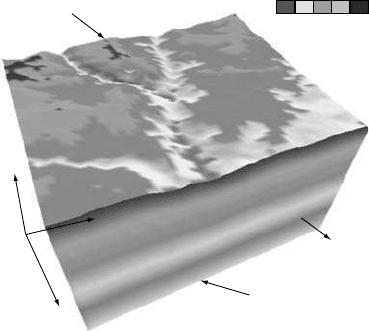
4.7 Boundary conditions 67
03
Elevation (km)
T = T
S
k dT/dz = q
m
z,v
z
dT/dn =0
x,v
x
y
,v
y
Fig. 4.4. The general problem of determining the temperature structure within
the crust including the effect of finite relief amplitude at the surface and tectonic
advection at a rate v
x
v
y
and v
z
. Usually one assumes a fixed temperature at the
surface of the Earth and a constant heat flux from the underlying mantle. The
side boundaries are isolated conductively.
underlying mantle and, if one considers the problem in more than one dimension,
no conductive heat loss through the side boundaries. The last condition imposes
that the temperature gradient in a direction normal to the ‘side walls’ must be zero,
unless heat is transported by advection through those walls, which is commonly
avoided by assuming that the advection velocity vector has no component in
a direction normal to the walls.
Note too that a fixed temperature condition does not need to be uniform in
space; for example, when temperature calculations are limited to the Earth’s crust,
where the range of temperature is of the order of a few hundred degrees, one may
need to take into account that the mean surface temperature is closer to 15 than
to 0
C. If one’s purpose is to determine the temperature history of rocks in order
to calculate their cooling age for a low-temperature thermochronometer such as
(U–Th)/He in apatite, one will need to take into account the atmospheric lapse
rate, i.e. the rate of change of temperature with altitude.
It is also worth mentioning that a ‘fixed-temperature’ boundary condition does
not need to be constant in time. For example, one may wish to study the rate and
depth of penetration of the temperature anomaly created by the diurnal or yearly
cycle in atmospheric temperature by imposing a cyclic variation in temperature
at the Earth’s surface (see Turcotte and Schubert (1982) for example).
