Браславский И.Я. Энергосберегающий асинхронный электропривод
Подождите немного. Документ загружается.

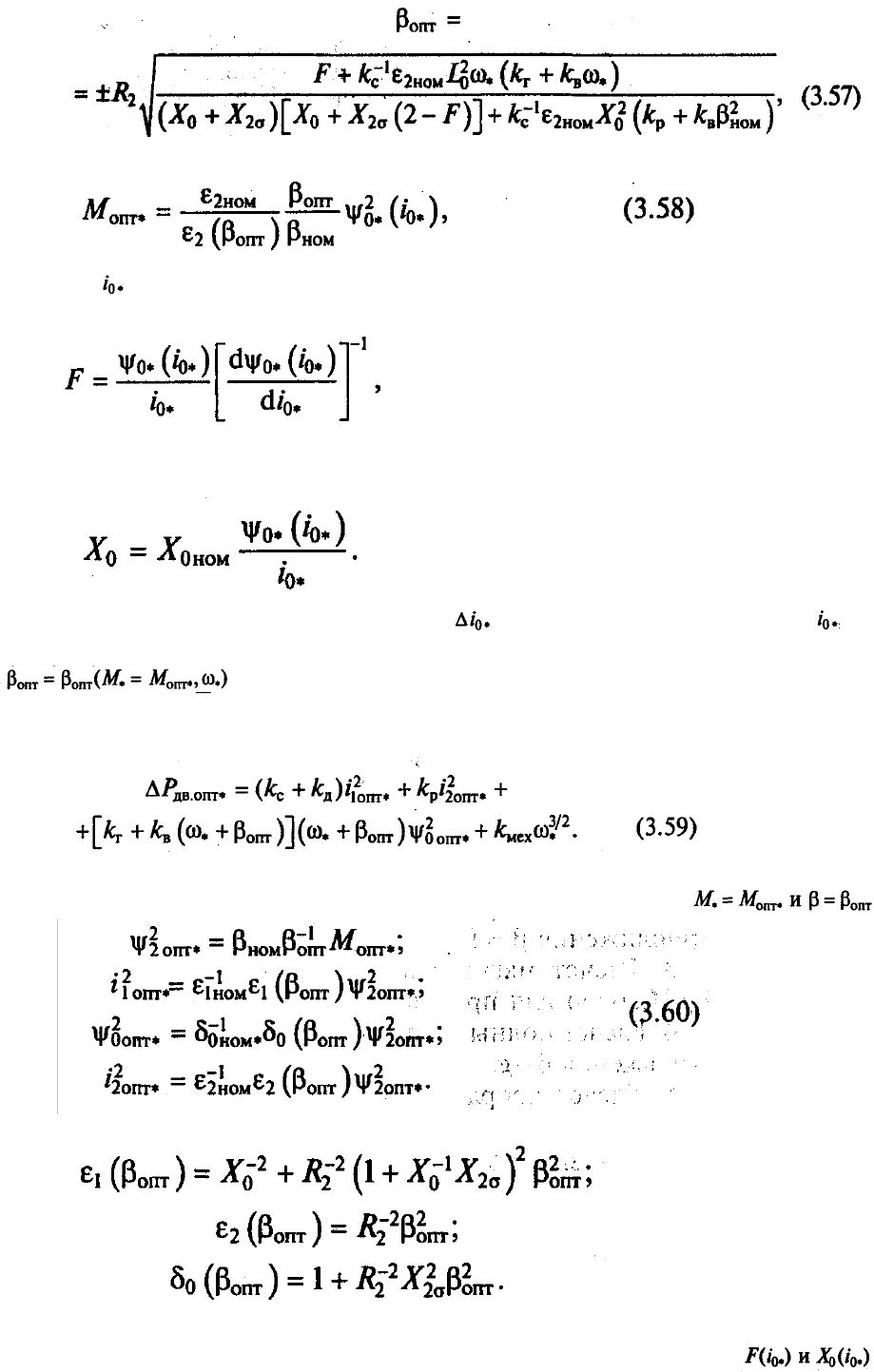
81
где — варьируемая величина.
Вспомогательная функция имеет вид
а индуктивное сопротивление, зависящее от насыщения двигателя по главному
магнитному пути,
Задаваясь последовательно с шагом промежуточной переменной , с помощью
выражений (3.57) и (3.58) можно найти закон оптимального управления в виде
,
обеспечивающий минимум суммарных потерь в двигателе. При
подстановке в выражение (3.26) оптимальных значений токов статора и ротора, а также
главного потокосцепления получим
Токи статора, ротора и главное потокосцепление в (3.59) рассчитываются по
формулам (3.7), (3.10) и (3.11) при подстановке в них значений :
Функции в формуле (3.60) можно записать в виде:
Отметим, что формулы (3.57) и (3.58) приемлемы при любом характере кривой
намагничивания, так как расчет входящих в них зависимостей
ведется
непосредственно по ее координатам.

82
Аналитические методы сравнительно просты, но применимы лишь для
ограниченного диапазона изменения момента нагрузки двигателя. При параметрической
форме представления закона оптимального управления усложняется решение задачи
сравнительной оценки эффективности законов частотного управления, когда по условиям
технологического процесса заданы момент и скорость двигателя. В этих случаях
целесообразно пользоваться численными алгоритмами поиска экстремума функции
потерь. Рассмотрим один из возможных численных методов.
При фиксированных значениях задача (3.55) сводится к
однопараметрическому поиску экстремума, при котором можно использовать методом
градиента как один из наиболее эффективных методов, отличающийся быстротой
сходимости итерационного процесса и применяемый для непрерывно дифференцируемых
выпуклых унимодальных функций. Рассмотрим вычислительную схему поиска экстремума
функции методом касательных.
Исходные данные
1. Параметры модели
.
2. Коэффициенты уравнения суммарных потерь
3. Параметры поиска экстремума методом касательных: коэффициент шага
4. Условия задачи — заданные значения момента .
Схема итерации
1. Расчет магнитного состояния АД и констант номинального режима
2. Установка условий задачи и начального приближения .
3. Расчет магнитного состояния
для приращения
скольжения .
4. Расчет полных потерь для приращения скольжения .
5. Расчет координат магнитного состояния АД
для приращения скольжения .
6. Расчет полных потерь
для приращения скольжения .
7. Расчет производной
8. Проверка условия поиска экстремума:
Если данное условие не выполняется, то , новое
приближение
и следует переход к п. 1. При выполнении условия поиск
заканчивается.
9. Вычисляются координаты магнитного состояния АД
и потери при оптимальном скольжении.
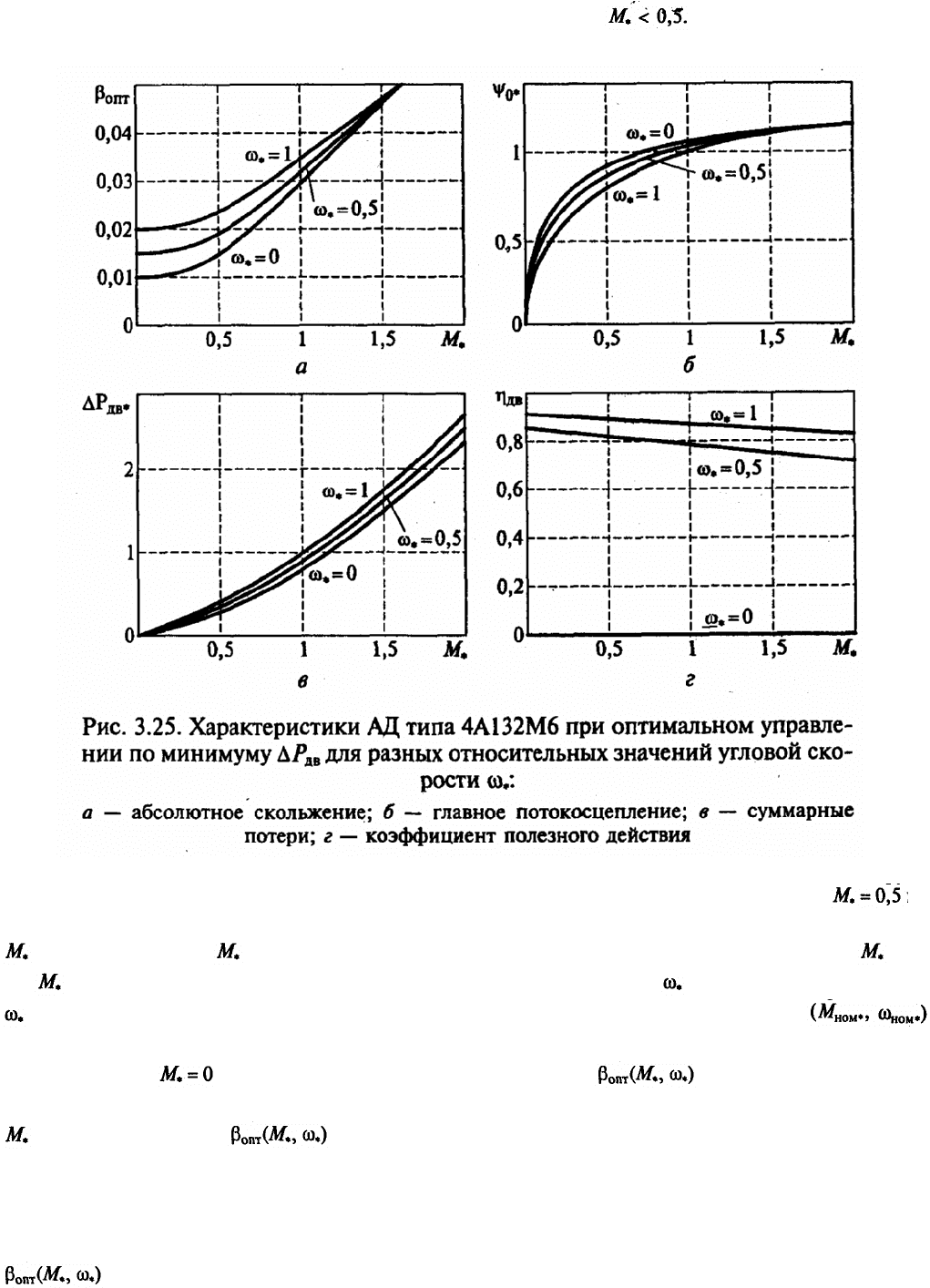
В качестве примера на рис. 3.25 приведены характеристики АД типа 4А132М6 при
оптимальном управлении по минимуму
для разных относительных значений угловой
скорости . Характеристики соответствуют фиксированным значениям скорости . При
постоянных значениях скорости
> 0,1 зависимость абсолютного скольжения от
момента является нелинейной (см. рис. 3.25, а),
причем с увеличением скорости
нелинейный участок зависимости охватывает все более широкий диапазон изменений
момента. Зависимость абсолютного скольжения от скорости наиболее сильно проявляется
83
в зоне малых значений момента нагрузки, т.е. при . В этой же области
скольжение менее всего зависит от изменения момента.
В нелинейной области характеристики намагничивания наибольшее влияние
оказывает момент нагрузки и в меньшей степени скорость двигателя. Так, при и
изменении скорости от со. = 0 до со. = 1 абсолютное скольжение возрастает в 1,46, при
= 1 в 1,36 и при
= 2,2 в 1,02 раза. При изменении нагрузки в диапазоне от
= 1
до
= 2,2 абсолютное скольжение возрастает при скорости = 1 в 2,34 раза, а при
= 0 в 5,15 раза. Величина оптимального абсолютного скольжения в точке
меньше номинального значения на 29 %.
В точке закон оптимального управления при всех значениях
скорости имеет конечный разрыв с односторонними пределами. При больших значениях
графики функции имеют практически линейный характер.
Чем больше значение момента и ниже скорость двигателя, тем более критично
изменяются потери в функции от абсолютного скольжения. Изменение момента
значительно сильнее влияет на величину абсолютного скольжения, соответствующего
минимуму потерь, чем при высоких значениях момента. Таким образом, анализ графиков
говорит о недопустимости пренебрежения зависимостью оптимального
абсолютного скольжения от момента двигателя.
Характеристики магнитного потока при управлении по минимуму потерь двигателя
(см. рис. 3.25,
б)
показывают, что при оптимальном управлении магнитный поток
84
изменяется в широких пределах и зависит как от момента, так и от скорости, т. е.
. На магнитный поток в большей мере оказывает влияние момент
нагрузки. Для двигателя 4А132М6 при и изменении момента от
поток двигателя увеличивается в 3,3 раза, а при = 0 в 2,2 раза. Изменение скорости
вращения двигателя в диапазоне от = 0 до = 1 незначительно влияет на величину
потока. С увеличением момента влияние скорости на поток уменьшается. Для
обеспечения режима минимальных потерь требуется форсирование магнитного потока
относительно его номинального значения, что достигается за счет увеличения
напряжения обмотки статора.
Характеристики потерь и коэффициента полезного действия
при оптимальном управлении представлены соответственно на рис. 3.25,
в
и
рис. 3.25,
г.
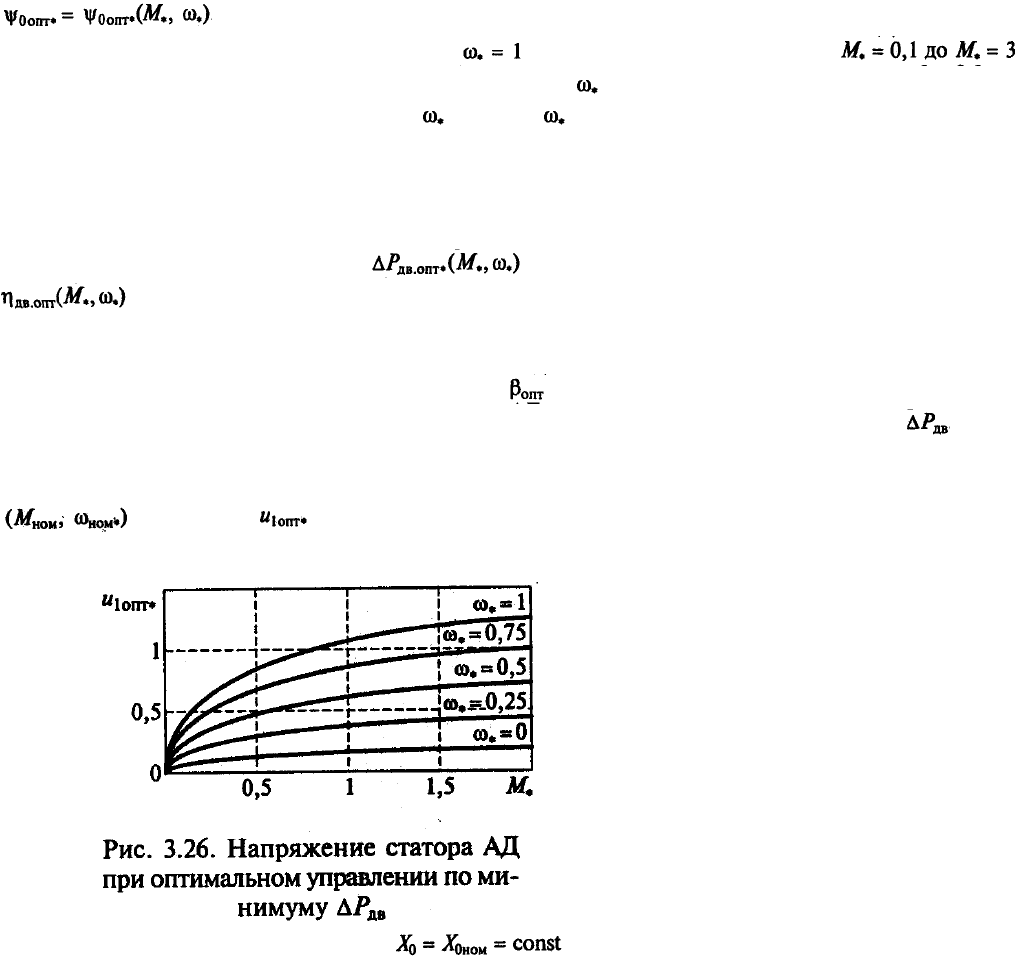
Напряжение статора в режиме минимальных потерь АД рассчитывается по
выражению (3.6) при подстановке в него . На рис. 3.26 показаны характеристики
напряжения статора АД при оптимальном управлении по минимуму . Эти
характеристики показывают, что для обеспечения оптимального режима к обмотке
статора должно быть приложено более высокое напряжение. Например, в точке
значение
превышает значение напряжения в номинальном режиме на
15 %.
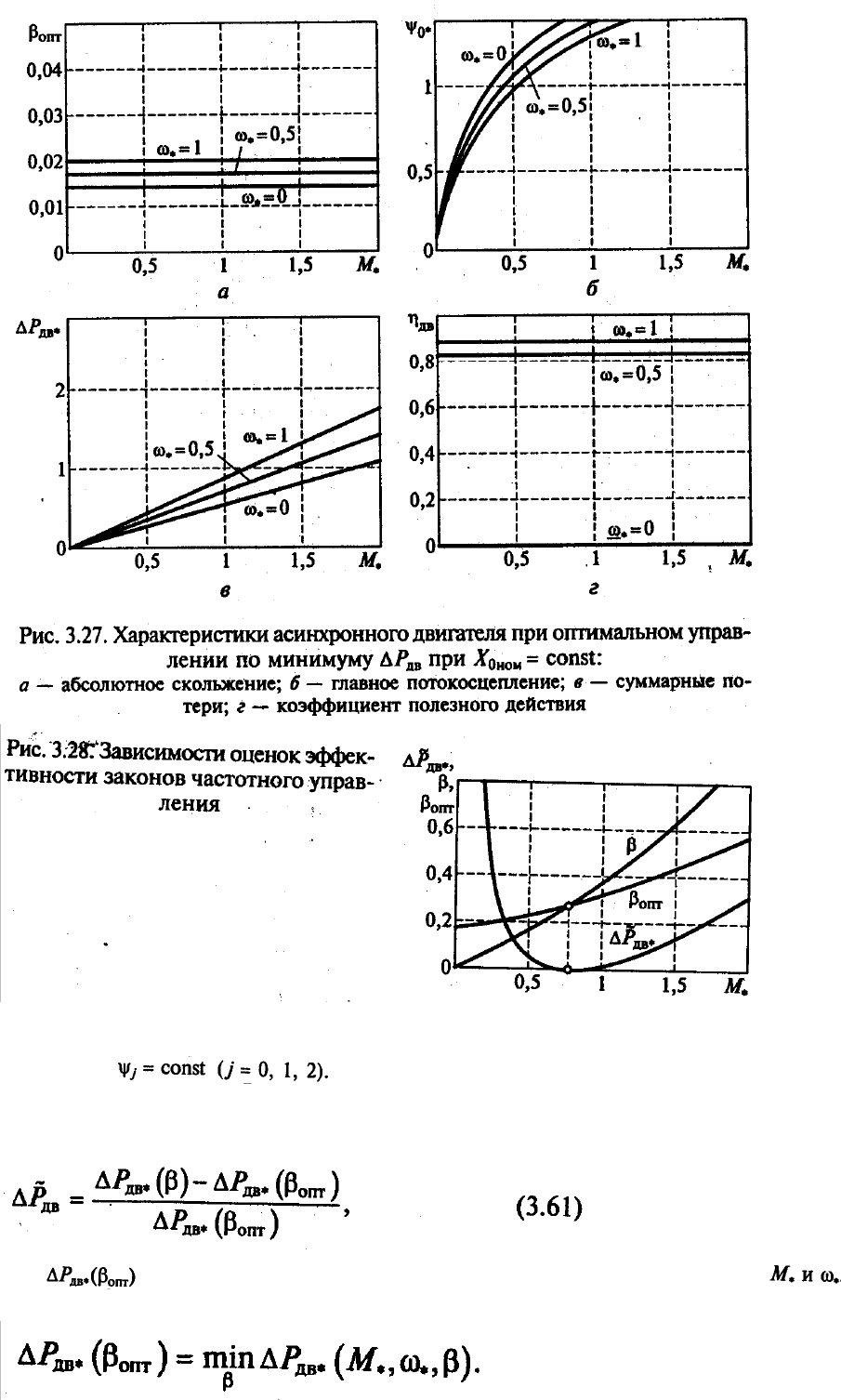
Режим минимальных потерь
иллюстрируется характеристиками АД,
представленными на рис. 3.27. Эти характеристики показывают, что для АД с линейной
характеристикой намагничивания (без учета насыщения) оптимальное скольжение не
зависит от момента двигателя и определяется угловой скоростью и параметрами АД. При
фиксированной скорости суммарные потери двигателя изменяются пропорционально
электромагнитному моменту, а КПД постоянен. Магнитный поток существенно возрастает
при
увеличении момента. Таким образом, пренебрежение насыщением АД по главному
магнитному пути искажает картину оптимального режима как в качественном, так и в
количественном отношении по сравнению с оптимальным режимом работы насыщенного
АД.
85
Практический интерес представляет сравнение оптимального управления по
минимуму суммарных потерь с законом пропорционального управления и режимами
управления при
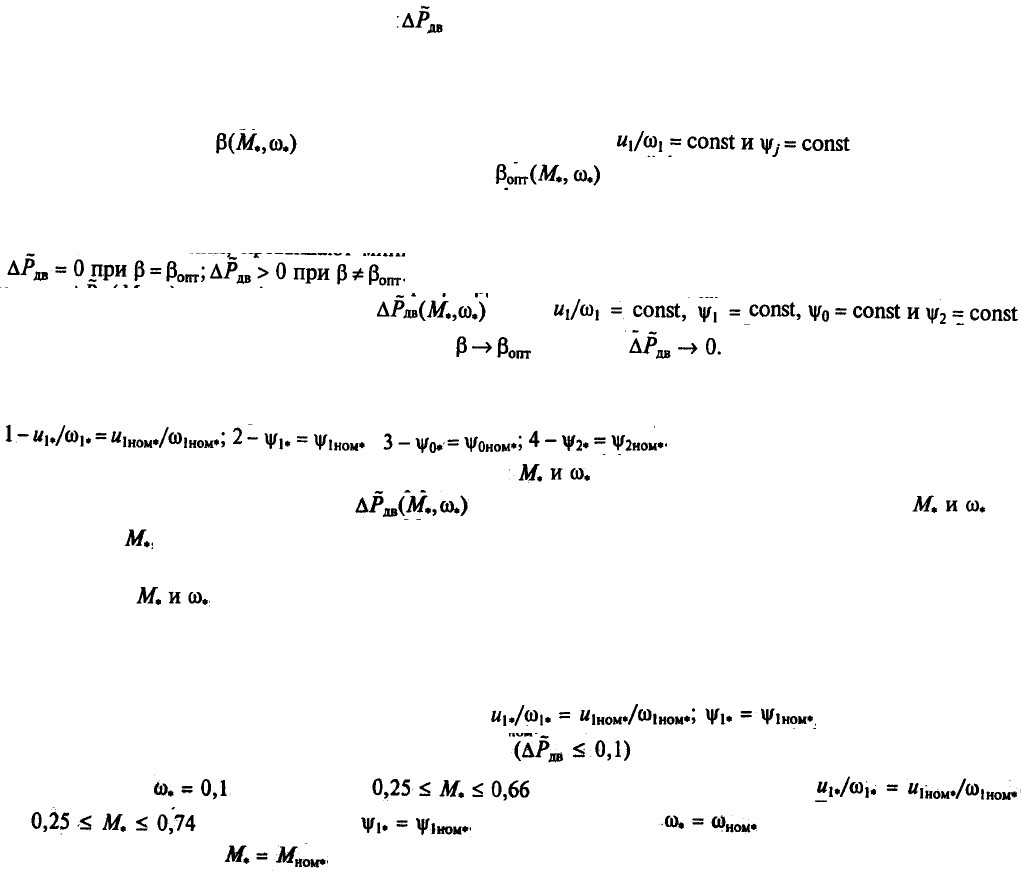
Введем меру эффективности законов управления по потерям АД, определяемую по
формуле
где — минимальное значение суммарных потерь при заданных .
Следовательно,
86
По степени приближения к нулю формула (3.61) позволяет оценить
эффективность различных законов частотного управления в сравнении с оптимальным
управлением по минимуму суммарных потерь АД.
Если области изменения момента нагрузки и скорости достаточно широки, то
графики функции , обеспечивающие режимы , имеют общие
точки с графиком оптимальной функции (рис. 3.28). В общих точках соот-
ветствующие оценки эффективности равны нулю, а при скольжениях, отличающихся от
оптимальных значений превышают минимальное значение, т. е.
.
Следовательно, функции при
имеют явно выраженный минимум. При оценка
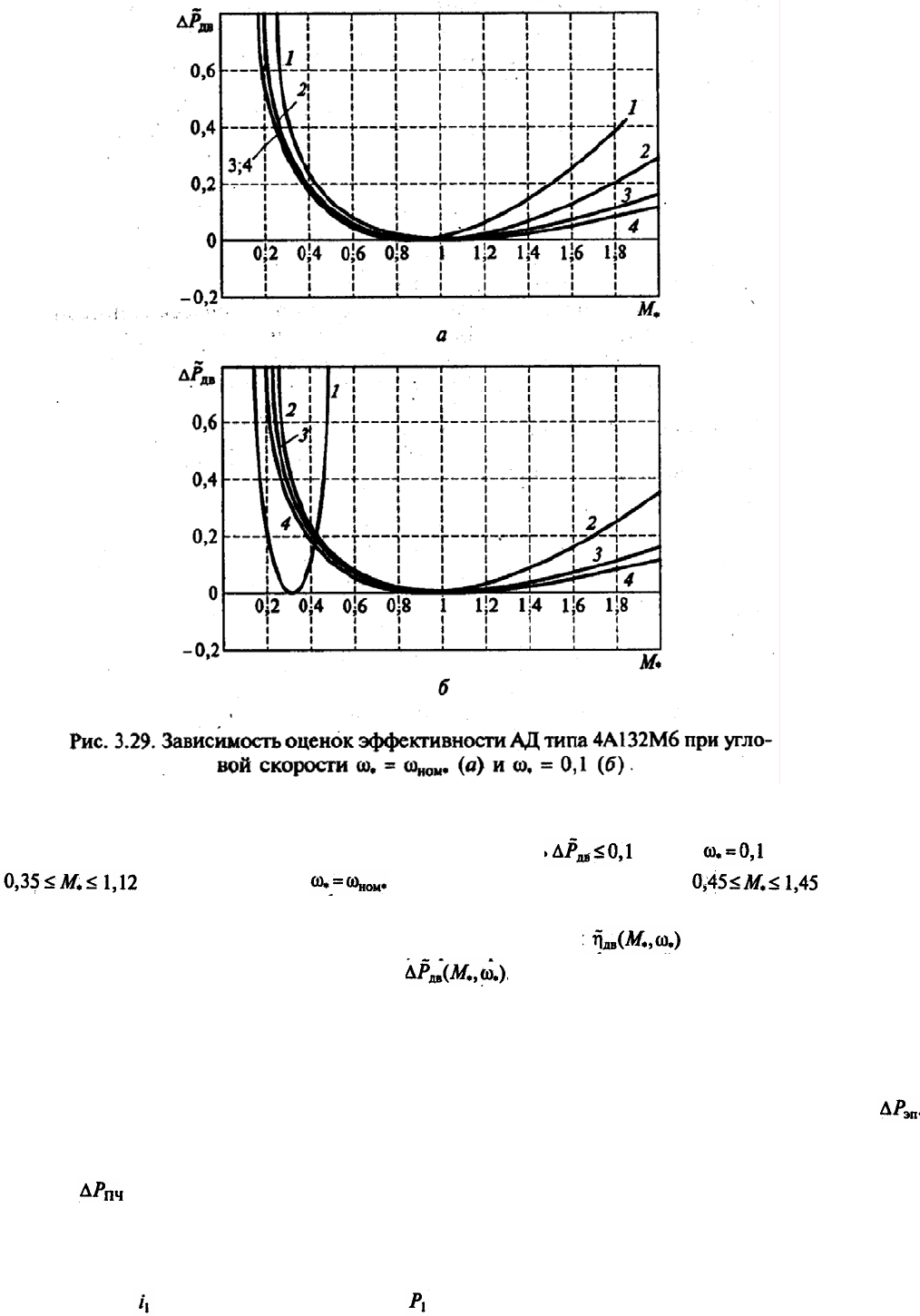
На рис. 3.29 приведены графики зависимости оценок эффективности АД типа
4А132М6 от угловой скорости для разных законов частотного управления:
; .
На рис. 3.29 видно, что при изменении оценки эффективности изменяются в
широких пределах. Значения сильно возрастают с уменьшением , а
также при
,
превышающих значение момента в номинальном режиме АД.
Вместе с тем для каждого закона частотного управления существуют области
изменения , в которых полные потери АД равны минимально возможным или
незначительно отличаются от них. Однако эти области ограничены сравнительно
небольшим диапазоном изменения момента и скорости, что свидетельствует о
рациональности применения закона оптимального управления по минимуму полных
потерь АД. Например, расчеты режимов показывают, что
при допуске в 10% на превышение потерь допустимый диапазон изменения
момента для составляет при законе управления
и при законе . Для скорости момент двигателя не
должен превышать
.
87
Режимы управления при постоянстве главного потокосцепления и полного
потокосцепления ротора имеют более широкий диапазон изменения момента,
удовлетворяющий допуску на превышение потерь : при он составляет
, а для скорости момент ограничен условием .
Аналогично формуле (3.61) вводится оценка эффективности закона частотного
управления по коэффициенту полезного действия
, характер изменения
которого отражает поведение функций
.
Сравнение различных законов частотного управления АД показывает преимущество
закона оптимального управления и целесообразность его осуществления в системах
автоматического управления электроприводами в тех случаях, когда угловая скорость и
момент двигателя изменяются в широких пределах.
Оптимизация режимов работы системы ПЧ—АД по минимуму суммарных потерь .
При постановке этой задачи представляет интерес исследование влияния режимов
двигателя на характеристики преобразователя частоты и в первую очередь на мощность
потерь .
Результаты исследований статических характеристик АД показывают, что
асинхронный двигатель как объект управления обладает экстремальными
характеристиками по ряду частных критериев качества. В том числе имеют экстремумы
ток статора
и активная мощность
двигателя, от которых зависят электрические
потери преобразователя частоты. Для решения задачи оптимизации режимов системы
ПЧ—АД по минимуму потерь преобразуем выражения (3.7) и (3.14), для чего в них вместо
88
потокосцепления ротора подставим
.
В результате получим следующие
зависимости тока статора и активной мощности от :
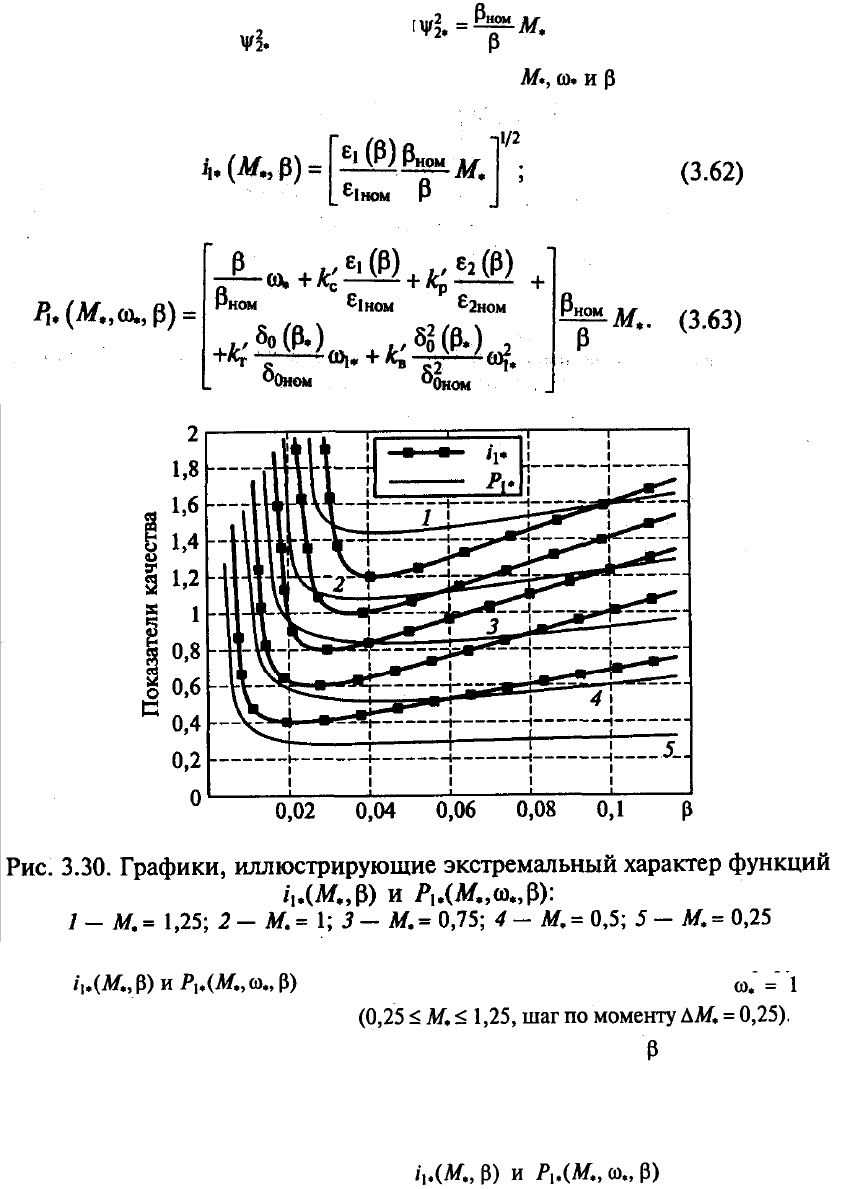
На рис. 3.30 приведены графики, иллюстрирующие экстремальный характер
функций
, рассчитанные для скорости и разных
фиксированных значений момента . Заметим, что
экстремумы активной мощности по варьируемой переменной
совпадают с экстремумом
функции полных потерь, так как при заданных значениях скорости и момента изменение
активной мощности при варьировании скольжением связано только с изменением потерь
в двигателе.
Экстремальный характер функций предопределяет наличие
экстремума функции электрических потерь ДПЧ с автономным инвертором напряжения
при питании его от неуправляемого выпрямителя. Запишем составляющие электрических
потерь преобразователя в относительных единицах с учетом формул (2.53), (2.58) и
(2.59), взяв в качестве базисной величину потерь при номинальном режиме работы
двигателя. Тогда относительные потери в выпрямителе и инверторе преобразователя
частоты определятся из следующих выражений:
89
характеризует удельный вес составляющих электрических потерь по отношению к
суммарным потерям двигателя при номинальном режиме работы.
Как следует из формул (3.64) и (3.65), потери в выпрямителе зависят от тока
статора, а потери в автономном инверторе — от тока статора и активной мощности
двигателя. Наличие экстремумов тока статора
и активной мощности
обусловливает
экстремальный характер отдельных составляющих электрических потерь выпрямителя
, инвертора и суммарных электрических потерь преобразователя . В
частности, режим минимальных потерь АД обеспечивает минимум электрических потерь в
источнике питания АИН.
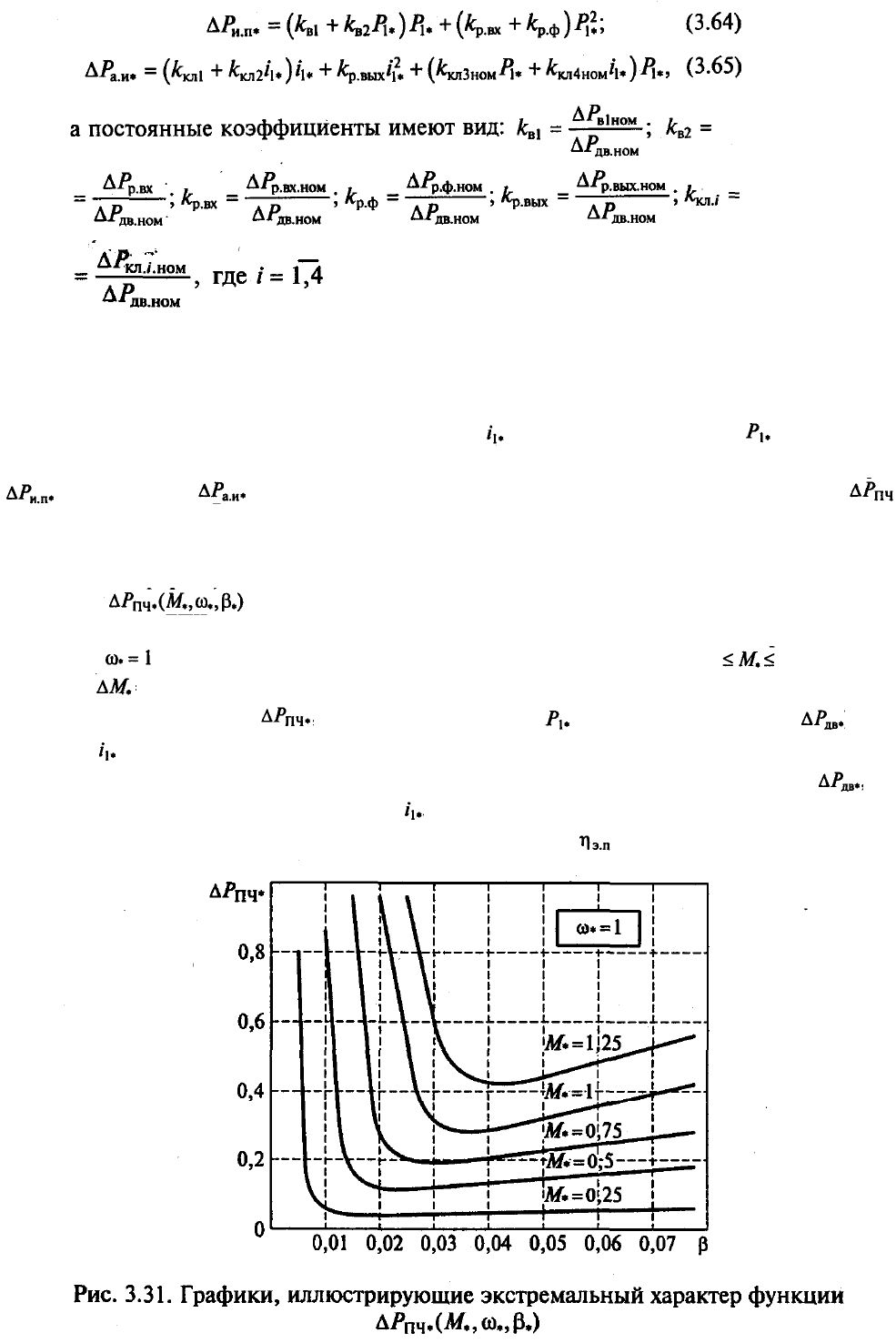
На рис. 3.31 приведены графики, иллюстрирующие экстремальный характер
функции . Экстремальные характеристики электрических потерь ДПЧ с
автономным инвертором напряжения рассчитаны по формулам (3.64) и (3.65) для
скорости и разных фиксированных значений момента (0,25
1,25, шаг по
моменту
= 0,25). В общем случае значения скольжения, доставляющие минимумы
электрическим потерям , активной мощности
(потерям двигателя ) и току
статора не совпадают. Однако отметим, что режим минимальных потерь ДР
П
ч>
достаточно близок как к оптимальному режиму по минимуму потерь двигателя , так и
к режиму минимального тока статора . К аналогичному выводу приходим, анализируя
характер поведения коэффициента полезного действия
.
90
Строгое решение задачи оптимизации режимов системы «преобразователь частоты
— асинхронный двигатель» без учета ограничений на управление может быть получено в
следующей ее постановке:
Оптимальное скольжение, обеспечивающее минимум функции потерь ,
определяется численными методами. Рассмотренный выше алгоритм поиска минимума
функции качества , базирующийся на методе касательных, сравнительно
просто обобщается на случай минимизации функции потерь системы ПЧ—АД.
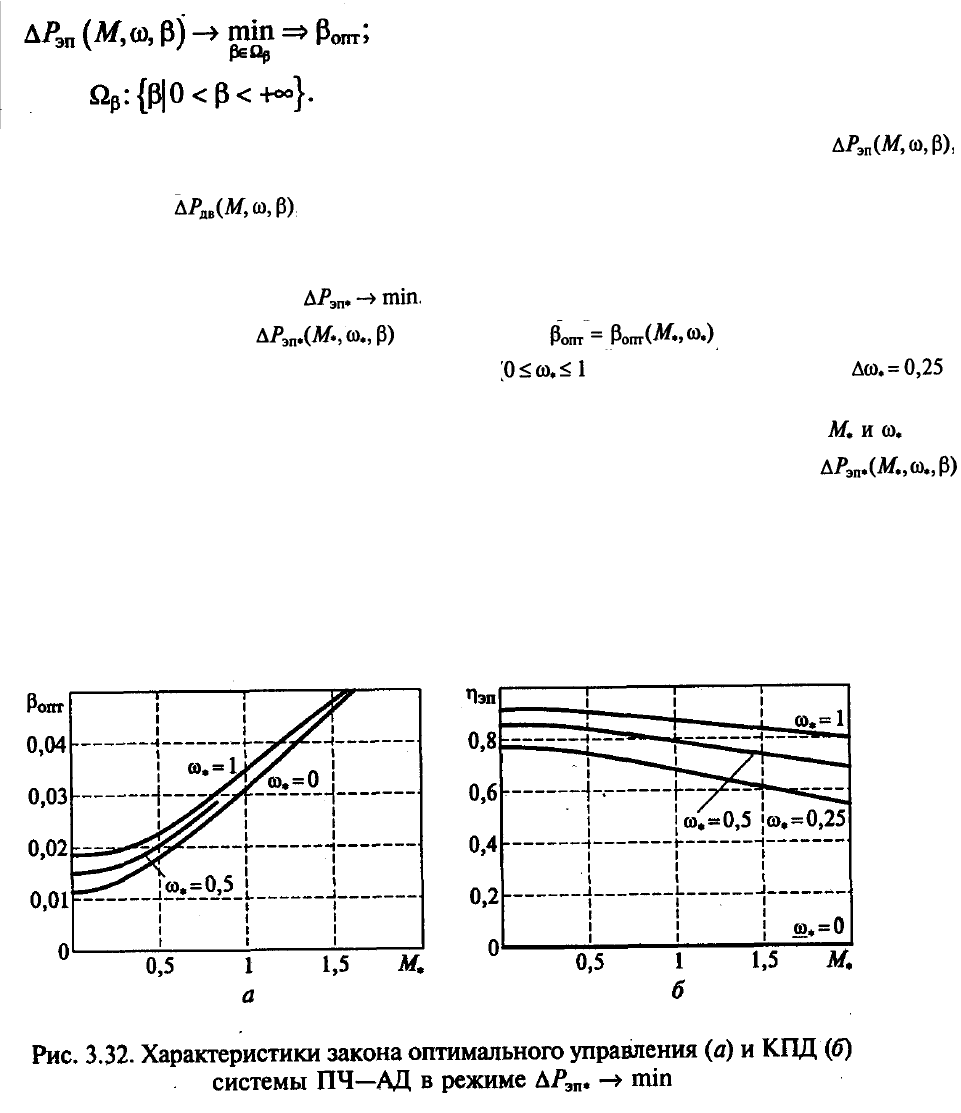
На рис. 3.32, показаны характеристики закона оптимального управления и КПД
системы ПЧ—АД в режиме . Приведенные на рис. 3.32,
а
графики
оптимального по минимуму управления рассчитаны для ряда
фиксированных значений угловой скорости ( , шаг по скорости ).
Сравнивая их с графиками оптимального по минимуму суммарных потерь АД управления,
находим качественное их совпадение. Зависимости КПД системы ПЧ—АД от (см.
рис. 3.32,
б)
показывают эффективность режима оптимального по минимуму
управления с энергетической точки зрения.
Таким образом, проведенный анализ возможностей оптимального по ряду
показателей управления частотно-регулируемым асинхронным двигателем и приведенные
общие количественные оценки, характеризующие разные законы оптимального
управления, позволяют обоснованно выбирать и внедрять необходимый закон управления
в зависимости от параметров и режимов работы АД.
