Borge D. -The Book of Risk

Подождите немного. Документ загружается.

Page 67

cooperate on risk management techniques that combine elements of both the insurance

markets and financial markets, such as bonds whose payments are linked to the occurrence

of natural catastrophes. When they finally started talking to each other, they were able to

create something new and useful for the world.

In the absence of a universal and comprehensive system for categorizing all risks, you can

try to place your particular risk situation in a context that many decision makers have faced

before and hope that your predecessors have already identified and categorized most of the

risks that you will be facing. If they have, you can get a head start by applying some of their

experience to your problem rather than starting from scratch. For example, borrowing from

the experience of others is likely to be possible if your risks are medical (deciding whether to

have elective surgery), political (deciding whether to run for governor), meteorological

(deciding whether to plant corn or soybeans this year), or geological (deciding whether to

build your house near a fault zone). In each of these disciplines, a wealth of risk information

is available for several types of preidentified risks. Although none of it is likely to fit your

situation exactly, you would be foolish to ignore it and you will probably make better

decisions by applying it with good judgment. By categorizing different risks, you can often

break a complex, amorphous blob of risks into smaller and simpler manageable parts.

In Chapter 6, we identify the major categories of risk facing a business enterprise.

Page 68

QUANTIFYING THE RISKS YOU FACE

We discussed the quantification of risks in Chapters 1, 2, and 3 when we introduced

decision trees and putting numbers on your beliefs about the probability of uncertain events

and the pleasure or pain you would feel if the events were to happen. We then discussed

volatility and correlation measures that could be useful in quantifying some kinds of risks in

practical situations.

In trying to quantify risks, however imperfectly, you are forced to think harder and more

concretely about your risk exposure than if you relied solely on hazy intuition or gut feel.

Having quantified your risks, you can take rationally calculated actions that are more closely

tailored to your particular situation and therefore more effective in moving you closer to your

desired risk profile. You can compare the magnitude of one risk against the magnitude of

another risk and decide how to trade some of one risk for some of the other. You can also

gauge how much risk you are taking in total, even if you are taking many different types of

risk.

PREVENTING RISKS

The most obvious risk management strategy is to prevent or avoid unwanted risks. Don't go

for a midnight walk in a high-crime neighborhood. Don't build your house on a flood plain.

Don't go cliff diving in Acapulco. Don't invest your life savings in Perpetual Motion

Incorporated at the urging of a stranger on the

Page 69

phone. Have your brakes checked before you go on a road trip through the Rocky

Mountains. The better you are at identifying and quantifying risks, the better you will be at

preventing or avoiding unwanted risks. You should not voluntarily take a risk that has no

potential to contribute to your welfare.

CREATING RISKS

just as you try to prevent or avoid unwanted risks, you want to create desirable risks.

Desirable risks are those embedded in attractive opportunities where you believe that the

potential gain outweighs the risks. Of course, it would be ideal if you could achieve a gain

without taking any risk, but life usually does not work that way. Opportunities usually come

with risks attached. As the saying goes, “Nothing ventured, nothing gained.”

Many people think that the goal of risk management is to eliminate risk—to be as cautious

as possible. Not so. The goal of risk management is to achieve the best possible balance of

opportunity and risk. Sometimes achieving this balance means exposing yourself to new risks

in order to take advantage of attractive opportunities.

BUYING OR SELLING RISKS

If you cannot prevent or avoid an unwanted risk, you may be able to sell it. If you cannot

create a desired risk, you may be able to buy it. Suppose that you are

Page 70

very worried about your house being swept away in a flood. Even though you are not able

to prevent a flood, you may be able to sell your house to someone who is not as worried

about floods as you are. The selling price may not be what you hoped for, but you can rid

yourself of the entire risk. If you are thrilled by the prospect of climbing Mount Everest, you

can buy a place on an expedition—buying a risk of death in order to gain a chance for

glory. Of course, we don't usually think of buying a risk in order to have the risk, but of

buying the opportunity and accepting the risk that comes with it. But since we are concerned

about risk management, it is useful to use this seemingly backward phrase to keep our terms

consistent.

DIVERSIFYING RISKS

You diversify risk when you don't put all your eggs in one basket. Diversification is a very

powerful way to manage risks and it has been practiced for centuries, in one form or

another. The power of diversification is that it can, in many cases, reduce risk substantially

without reducing the expected gain, thus making diversification one of the few free lunches

available in life.

For example, in situations where outcomes are not highly correlated with each other,

diversification can provide substantial risk reduction benefits. Many believe that the stock

market fits this description reasonably well and therefore that diversification of stock

holdings is a good idea. As we show in

Page 71

Chapter 6, dividing your portfolio among 20 or 30 or more stocks substantially reduces the

volatility of portfolio returns without sacrificing expected portfolio returns.

To understand the effects of diversification, consider the following example. Imagine that

you are the ruler of a colonial empire. You have amassed a large cache of gold, worth $100

million, in a faraway colony and must transport it across a vast ocean to bring it home. All

the gold would fit in a single ship, but you have many ships available. All the ships will be

sailing anyway, whether or not they carry any of the gold, so there is no extra shipping cost if

you use more than one ship for the gold. You know from experience that two out of every

ten ships has been lost making the dangerous crossing so you assign a 20 percent

probability to any single ship sinking. You face a risk decision: should you put all your gold in

one ship or spread it across two ships? Let's look at the decision tree for each strategy as

shown in Figure 4.1.

We are assuming that the fate of each ship is independent of the fate of the other. Losing

one ship makes it no more or less likely that we will lose the other ship. They won't be lost in

the same storm, for example. In other words, the fates of the ships are not correlated with

each other. This lack of correlation is what allows diversification to work.

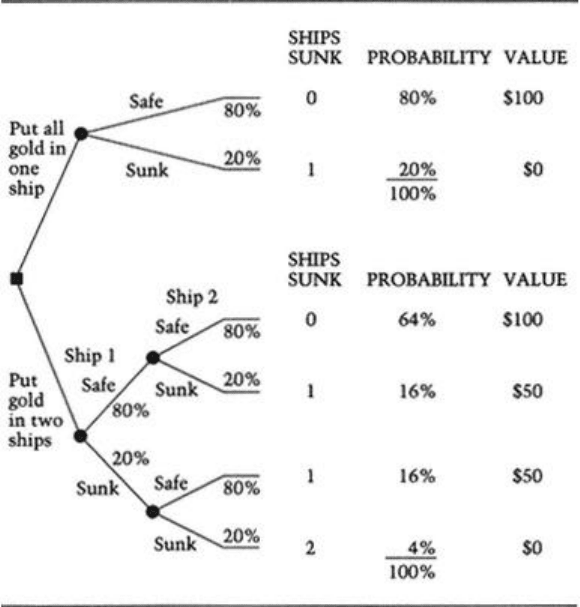
If you put all the gold on one ship, there is a 20 percent chance of losing it all and an 80

percent chance of saving it all. If you put $50 million of gold into each of two ships, there is

a 4 percent chance of losing both ships (a $100 million loss), a 32 percent

Page 72

Figure 4.1

One Ship or Two? Possible Outcomes

chance of losing one ship and saving one ship (a $50 million loss), and a 64 percent chance

of saving both ships (no loss).

Which strategy do you prefer? By diversifying, the two-ship strategy dramatically reduces

the chance of losing $100 million (from 20 percent to 4 percent) but also reduces the

probability of saving it all (from

Page 73

80 percent to 64 percent). Both strategies produce the same “expected” value of $80

million of the gold being saved, meaning that if you repeated each strategy 1,000 times you

would, on average, save $80 million of the gold using either strategy. Unfortunately, you

won't be doing this 1,000 times. You have only one shot, and the outcome is very uncertain.

If you are risk averse, you might be more anxious to avoid disaster than to hold out for the

best possible outcome.

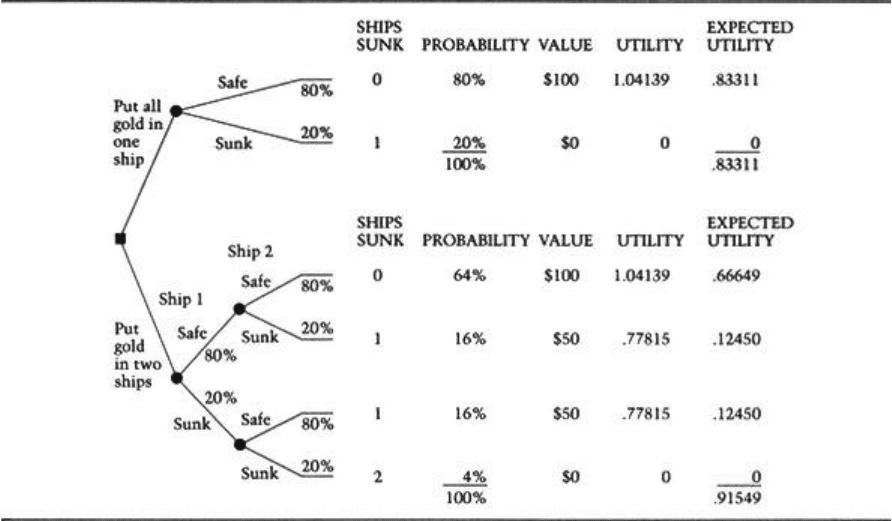
To know if and to what degree you are risk averse, we need to assess your utility for

wealth in this situation. Since we went through a similar process in an earlier example, we

won't go through all the steps here. Assume that we have your utility function for wealth and

use it to complete your decision tree as shown in Figure 4.2.

Now we now know that the diversifying two-ship strategy is better, for you, than the go-

for-broke, one-ship strategy. We know this because the two-ship strategy offers you a higher

expected utility. Given your probability assessments and preferences, the likely pain of losing

everything was more important than the likely pleasure of preserving everything.

Two ships provide some diversification, but four ships would provide even more. The

probability of losing all the gold is reduced from 4 percent (.2 x .2) with two ships to 0.16

percent with four ships (.2 x .2 x .2 x .2). But the four-ship strategy also reduces the chance

of saving all the gold from 64 percent (. 8 x .8) with two ships to 41 percent (. 8 x .8 x .8

x .8) with four ships. Even though it gives you less than a 50–50 chance of saving all the

gold, would a four-ship strategy be a better decision for you than the

Page 74

Figure 4.2

One Ship or Two? Decision Tree

Page 75

two-ship strategy? Yes, it would. The expected utility of a four-ship strategy is higher than

that of the two-ship strategy. In fact, if diversification were free (as we have assumed here),

you would send as many ships as you had. In real life, diversification is usually not free and

at some point further diversification would not be worth the extra cost.

CONCENTRATING RISKS

You concentrate risk when you put all your eggs in one basket and according to Bernard

Baruch, “you watch the basket.’’ Why would you ever want to concentrate risk when

diversifying risk is supposed to be such a good thing? One such case is when you would

rather preserve the possibility of extremely good outcomes than reduce the probabilities of

very bad outcomes. Another case is when you can actually increase the odds of good

outcomes by focusing your attention and effort on managing a few opportunities rather than

spreading yourself too thin managing many opportunities. We are assuming that you have

some positive influence over the outcomes. If you do not, you should not overlook the

probable benefits of diversifying.

For example, a large investor who is actively involved in the management of a company

has influence over what the company does and how successful it will be. The large investor

may be better off putting a substantial fraction of his portfolio in that company in order to

gain maximum influence on

Page 76

management and to focus his limited time on working with the company. A small investor has

no such influence and would gain nothing by putting a large fraction of his wealth in that

company.

HEDGING RISKS

Hedging is another way of dealing with unwanted risks. You hedge when you acquire a new

risk that exactly offsets the unwanted risk, leaving you with no risk. Since each outcome of

the hedge exactly off-sets each outcome of the unwanted risk, the net outcome is always

zero. This is called a perfect hedge and is just as effective as selling the risk.

Consider this simple example of a perfect hedge. The Knicks are playing the Celtics in a

basketball game. You have bet $100 on the Knicks winning. But now you are having

second thoughts about the wisdom of betting on this game. You hedge your unwanted bet on

the Knicks by placing another bet of $100 on the Celtics. This strategy works because if the

Knicks win, the Celtics must lose and vice versa. If the Knicks win, you win $100 on the

Knicks bet and lose $100 on the Celtics bet, so the net outcome is zero. If the Celtics win,

you win $100 on the Celtics bet and lose $100 on the Knicks bet. Again, the net outcome is

zero. Your perfectly hedged bet is just like no bet at all.

Unfortunately, it is not easy to find a costless, perfect hedge. Most real hedges either cost

something to acquire or do not exactly hedge you against all out-