Бораковський О.В. Вища математика: конспект лекцій, модуль І
Подождите немного. Документ загружается.

81
Таким чином, скалярний добуток двох векторів дорівнює добутку
довжини одного з них на проекцію другого на напрямок першого.
Властивості скалярного добутку:
1) комутативність
(
)
(
)
abba ,, =
:
(
)
(
)
bababa ,cos, ⋅⋅= , а
(
)
(
)
ababab ,cos, ⋅⋅= .
Так як abba ⋅=⋅ як добуток чисел і
(
)
(
)
abba ,cos,cos = .
2) асоціативність відносно множника на число ),()( baba
λλ
=⋅ :
),()( baaПрbaПрbba
bb
λλλλ
=⋅⋅=⋅=⋅ .
3) операції додавання і скалярного множення векторів зв’язані
дистрибутивним законом множення відносно додавання (розподільча
властивість):
cabacba +=+ )(
.
=⋅+⋅=+⋅=+⋅=+ cПрabПрacПрbПрacbПрacba
aaaaa
)()()(
c
a
b
a
+
=
.
4) скалярний квадрат вектора дорівнює квадрату його довжини:
2
2
0cos aaaaaaaa =⋅=⋅⋅=⋅=
.
звідси 1
222
=== kji .
5)
0
=
⋅
b
a
, якщо 0=a , або 0=b , або ba ⊥
.
Звідси 0=== ikkjji .
Ураховуючи властивості 4) і 5), якщо
kajaiaa
zyx
++=
та
kbjbibb
zyx
++=
, то
zzyyxx
babababa ++=
.

82
Косинус кута між векторами
a
і
b
обчислюється за формулою:
222222
,
cos
zyxzyx
zzyyxx
bbbaaa
bababa
ba
ba
++++
+
+
=
⋅
=
ϕ
.
Звідси умова перпендикулярності векторів
a
і
b
:
0=++⇔⊥
zzyyxx
babababa .
З фізичної точки зору скалярний добуток постійної сили
F
та путі
S
є
робота
)cos( SFSFA ⋅= .
Приклад. Обчислити )()35( baba −⋅+ , якщо 2a = , 2b = ,
b
a
⊥
.
Розв’язання. =−⋅+⋅−=−⋅+
22
3355)()35( babbaababa
8
12
20
3
5
22
=
−
=
−
=
b
a
.
Приклад. Знайти одиничний вектор, того ж напряму, що й вектор
kjia 22 +−= .
Розв’язання. Знайдемо модуль вектора
a
:
392)2(1
222
==+−+=a . Тоді
kji
a
a
a
3
2
3
2
3
1
0
+−== .
Перевіримо 1
9
9
9
4
9
4
9
1
0
==++=a .
Векторний добуток векторів. Векторним добутком двох векторів
a
і
b
,
який позначають ],[ ba або
b
a
×
, є вектор
c
(рис. 24), що визначається
такими трьома умовами:

83
a
r
ϕ
c
r
b
r
Рис. 24
1) вектор
c
перпендикулярний як до
a
так і до
b
, тобто
a
c
⊥
і
b
c
⊥
;
2) довжина вектора
c
чисельно дорівнює площі паралелограма,
побудованого на векторах
a
і
b
: ),sin( babac ⋅⋅= ;
3) вектори
a
,
b
і
c
, що не належать одній площині (не колінеарні),
утворюють праву тройку; тобто, якщо дивитись з кінця вектора
c
найкоротший поворот від вектора
a
до вектора
b
здійснюється проти руху
годинникової стрілки і ліву – якщо за рухом годинникової стрілки.
Властивості векторного добутку:
1) зміна місця множників дає протилежний вектор
a
b
b
a
×
−
=
×
;
2) вектори
b
a
×
і
a
b
×
колінеарні, мають одинакові модулі (площа
паралелограма таж сама), але протилежно спрямовані (трійки векторів
a
,
b
,
b
a
×
і
a
,
b
,
a
b
×
протилежно орієнтовані).
Отже
a
b
b
a
×−=× ;
3) асоціативність відносно скалярного множника:
)()()( bababa
λλλ
×=×=× .
Нехай
0
>
λ
, вектор )ba( ×
λ
перпендикулярний до векторів
a
і
b
,
вектор b)a( ×
λ
також перпендикулярний до векторів
a
і
b
(вектори
a
і
a
λ
належать одній площині). Отже вектори )ba( ×
λ
і b)a( ×
λ
колінеарні і
напрямки їх співпадають. Вони мають однакову довжину:
84
),sin()( babababa ⋅⋅=×=×
λλλ
і
),sin(),sin()( bababababa ⋅⋅=⋅×=×
λλλλ
.
Звідси baba ×=×
λλ
)( .
Доведення при
0
<
λ
аналогічне;
3) два ненульових вектори
a
і
b
колінеарні тоді й тільки тоді, коли їх
векторний добуток дорівнює нулю 0|| =×⇔ baba .
Якщо b||a , то кут між ними дорівнює
°
0
або
°
180
. Але тоді
0),sin( =⋅⋅=× bababa . Отже
0
=
×
b
a
.
Якщо ж
0
b
a
=× , то 0)b,asin(ba =⋅× . Але тоді 0, == ba
ϕ
або
°
=
180
ϕ
, тобто
b||a
.
Зокрема 0
=×+×+× kkjjii
;
3) векторний добуток має розподільчу властивість:
cbcac)ba( ×+×=×+
.
Векторний добуток векторів
kajaiaa
zyx
++=
і
kbjbibb
zyx
++=
обчислюється за формулою:
zyx
zyx
bbb
aaa
kji
ba =×
.
Ця формула перевіряється безпосереднім перемноженням двох
векторів.
Звідси встановлення колінеарності векторів
a
і
b
:
b||a
b
a
b
a
b
a
z
z
y
y
x
x
⇔==
.
85
Площа паралелограма, побудованого на векторах
a
і
b
, дорівнює
),sin( bababaS
пар
⋅⋅=×= , а площа трикутника
baS ×=
2
1
∆
.
Приклад.
Обчислити площу трикутника, побудованого на векторах
kjia 236 −+= і kjib 623 +−= .
Розв’язання. Знайдемо векторний добуток:
kjikji
kji
ba 214214
23
36
63
26
62
23
623
236 −−=
−
+
−
−
−
−
=
−
−=× .
Тоді
2
49
214214
2
1
2
1
222
=++=×= baS
∆
(кв. од.).
Приклад. Обчислити площу паралелограма, що побудований на
векторах
b
a
3
+
і
b
a
+
3
, якщо 1== ba , °= 30),( ba
.
Розв’язання.
Маємо =+×+ )3()3( baba
=
×
+
×
+
×
+
×
b
b
a
b
b
a
a
a
3
9
3
b
a
×
−
=
8
.
Тоді 4
2
1
11830sin88 =⋅⋅⋅=°⋅⋅=×= babaS (кв. од.).
Мішаний добуток трьох векторів.
Мішаним добутком трьох векторів
b,a і c називається скалярний добуток вектора
b
a
×
на вектор c тобто
c)ba( ⋅× .
Позначається cba .
Модуль мішаного добутку векторів cba дорівнює об’єму
паралелепіпеда, побудованого на цих векторах, які відкладені від однієї
точки:
cbaV =
.
86
Властивості мішаного добутку:
1) мішаний добуток трьох векторів дорівнює нулю, якщо:
а) хоча б один з цих векторів дорівнює нулю;
б) два з векторів паралельні (колінеарні);
в) усі три вектори паралельні одній площині (компланарні);
2) мішаний добуток не зміниться, якщо у ньому змінити місцями знаки
векторного і скалярного множення, тобто
cbacbacba =×⋅=⋅× )()(
;
3) мішаний добуток не зміниться при круговій перестановці векторів
bacacbcba == ;
4) при перестановці будь-яких двох векторів мішаний добуток змінить тільки
знак: cbabca;cbaabc;cbacab −=−=−= .
Мішаний добуток векторів:
kajaiaa
zyx
++=
,
kbjbibb
zyx
++=
,
kcjcicc
zyx
++= обчислюється за формулою
zyx
zyx
zyx
ccc
bbb
aaa
cba =
.
З властивостей мішаного добутку трьох ненульових векторів випливає
необхідна і достатня умова компланарності: 0=cba .
Припустимо, що це так. Тоді можливо було б побудувати паралелепіпед з
об’ємом
0
≠
V
. Але Vcba ±= , тоді 0≠cba а це суперечить умові 0=cba .
Навпаки, нехай cba ,, – компланарні. Тоді вектор
b
a
d
×
=
–
перпендикулярний до площини, якій належать (або паралельні) вектори
cba ,, і
c
d
⊥
.
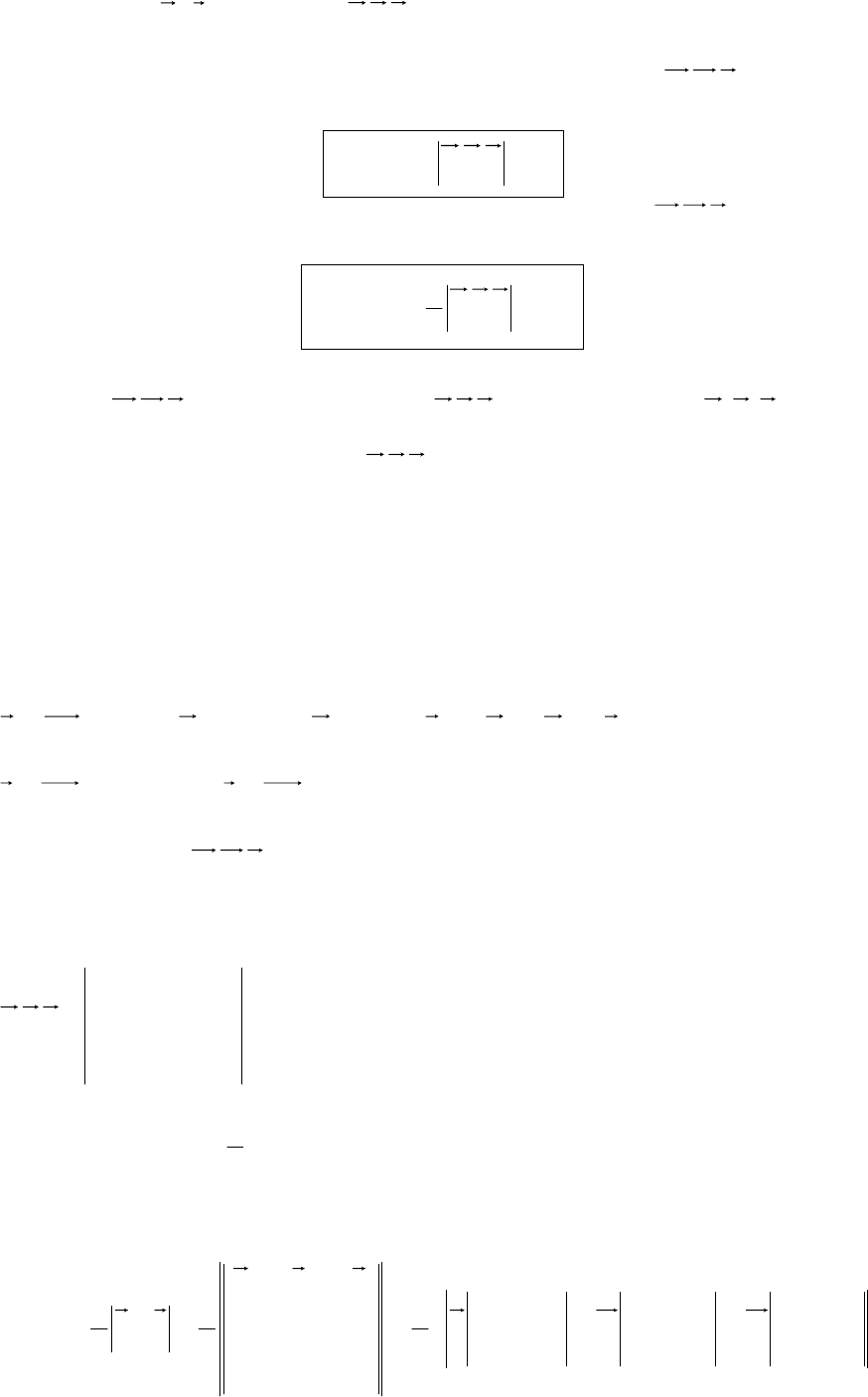
87
Звідси
(
)
0cd =⋅
, тобто 0=cba .
Об’єм паралелепіпеда, побудованого на векторах cba ,, дорівнює
cbaV
пар
=
.
Об’єм трикутної піраміди, що побудована на векторах cba ,, дорівнює:
cbaV
пір
6
1
=
.
Мішаний добуток дає можливість визначити взаємну орієнтацію
векторів cba ,, у просторі. Якщо 0>cba , то вектори cba ,, утворюють
праву тройку векторів, а якщо 0<cba , – ліву.
Приклад. Обчислити об’єм піраміди, яка має вершину у точках:
)
3
;
2
;
1
(
A
;
)
1
;
1
;
0
(
−
B
;
)
2
;
5
;
2
(
C
;
)
2
;
0
;
3
(
−
D
. Знайти площу грані
ABC
і косинус
кута
BAD
.
Розв’язання. Складемо вектори:
)2;3;1(23)31()21()10( −−−=−−−=−+−−+−== kjikjiABa ;
)1;3;1( −== ACb ; )5;2;2( −−== ADc .
Знайдемо cba ,, :
24152124615
522
131
231
=−++++=
−−
−
−
−
−
=cba .
Звідси 424
6
1
=⋅=
пір
V (куб. од.).
Площа грані
ABC
дорівнює:
31
31
11
21
13
23
2
1
131
231
2
1
2
1
−−
+
−
−−
−
−
−−
=
−
−−−=×= kji
kji
baS
ABC
=

88
10
2
3
2
90
39
2
1
039
2
1
22
==+=+−= kji (кв. од.).
Косинус кута
BAD
– це косинус кута між векторами
a
AB
=
і
c
AD
=
.
Звідси 651,0
33
14
3314
14
522231
1062
),cos(
222222
≈==
++++
++−
=
⋅
⋅
=
ca
ca
ca .
5. Пряма лінія і площина у просторі. Поверхні другого порядку
Площина. Нормальне рівняння площини у векторній формі має
вигляд:
ρ
=⋅ nr
,
де
r xi yj zk
= + +
r
r r
r
радіус-вектор довільної точки
( , , )
M x y z
площини;
cos cos cos
n i j k
α β γ
= + +
r
r r
r
– одиничний вектор, що має напрямок
перпендикуляра до площини, проведений з початку координат;
, ,
α β γ
–
кути, що утворюються цим перпендикуляром з осями координат;
ρ
–
довжина цього перпендикуляра. Переходячи до координат у скалярному
добутку, отримаємо нормальне рівняння площини у координатній формі:
cos cos cos 0
x y z
α β γ ρ
+ + − =
,
Будь-яке рівняння першого степеня
0
Ax By Cz D
+ + + =
, при умові
2 2 2
0
A B C
+ + ≠
, задає площину у просторі і має назву загального рівняння
площини. Коефіцієнти
, ,
A B C
– можна розглядати, як компоненти вектора
нормалі
N Ai Bj Ck
= + +
r
r
r r
до площини.
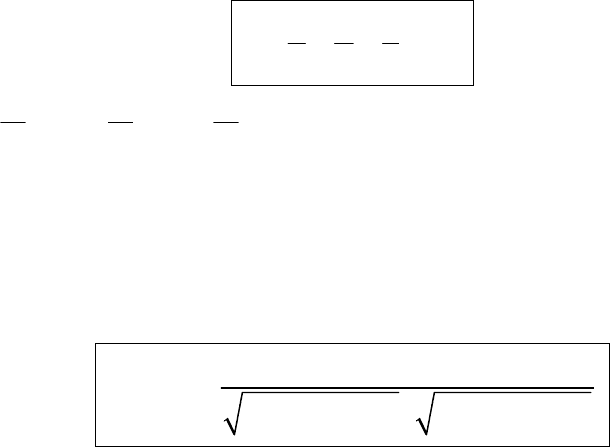
Для отримання нормального рівняння, треба загальне рівняння
площини помножити на нормуючий множник
2 2 2
1 1
N
A B C
µ
= ± = ±
+ +
,
знак якого обирається з умови
0
<
D
µ
, тобто знаки
µ
і
D
протилежні.
Розглянемо часткові випадки розташування площини
0
=
+
+
+
D
Cz
By
Ax
, у просторі:
89
0
=
A
; площина паралельна осі
Ox
;
0
=
B
; площина паралельна осі
Oy
;
0
=
C
; площина паралельна осі
Oz
;
0
=
D
; площина проходить через початок координат;
0
=
=
B
A
; площина перпендикулярна осі
Oz
(паралельна площині
xOy
);
0
=
=
C
A
; площина перпендикулярна осі
Oy
(паралельна площині
xOz
);
0
=
=
C
B
; площина перпендикулярна осі
Ox
(паралельна площині
yOz
);
0
=
=
D
A
; площина проходить через ось
Ox
;
0
=
=
D
B
; площина проходить через ось
Oy
;
0
=
=
D
C
; площина проходить через ось
Oz
;
0
=
=
=
D
B
A
; співпадає за площиною
xOy
(
0
=
z
);
0
=
=
=
D
C
A
; співпадає за площиною
xOz
(
0
=
y
);
0
=
=
=
D
C
B
; співпадає за площиною
yOz
(
0
=
x
);
Якщо у загальному рівнянні площини
0
≠
D
(тобто площина не
проходить через початок координат), то поділивши усі частини рівняння на
D
−
, отримаємо рівняння площини у відрізках
1=++
c
z
b
y
a
x
,
де
A
D
a −=
;
B
D
b −=
;
C
D
c −=
– точки перетину площини з осями
Ox
,
Oy
,
Oz
.
Кут
ϕ
між площинами
0
1
1
1
1
=
+
+
+
DzCyBxA ,
2 2 2 2
0
A x B y C z D
+ + + =
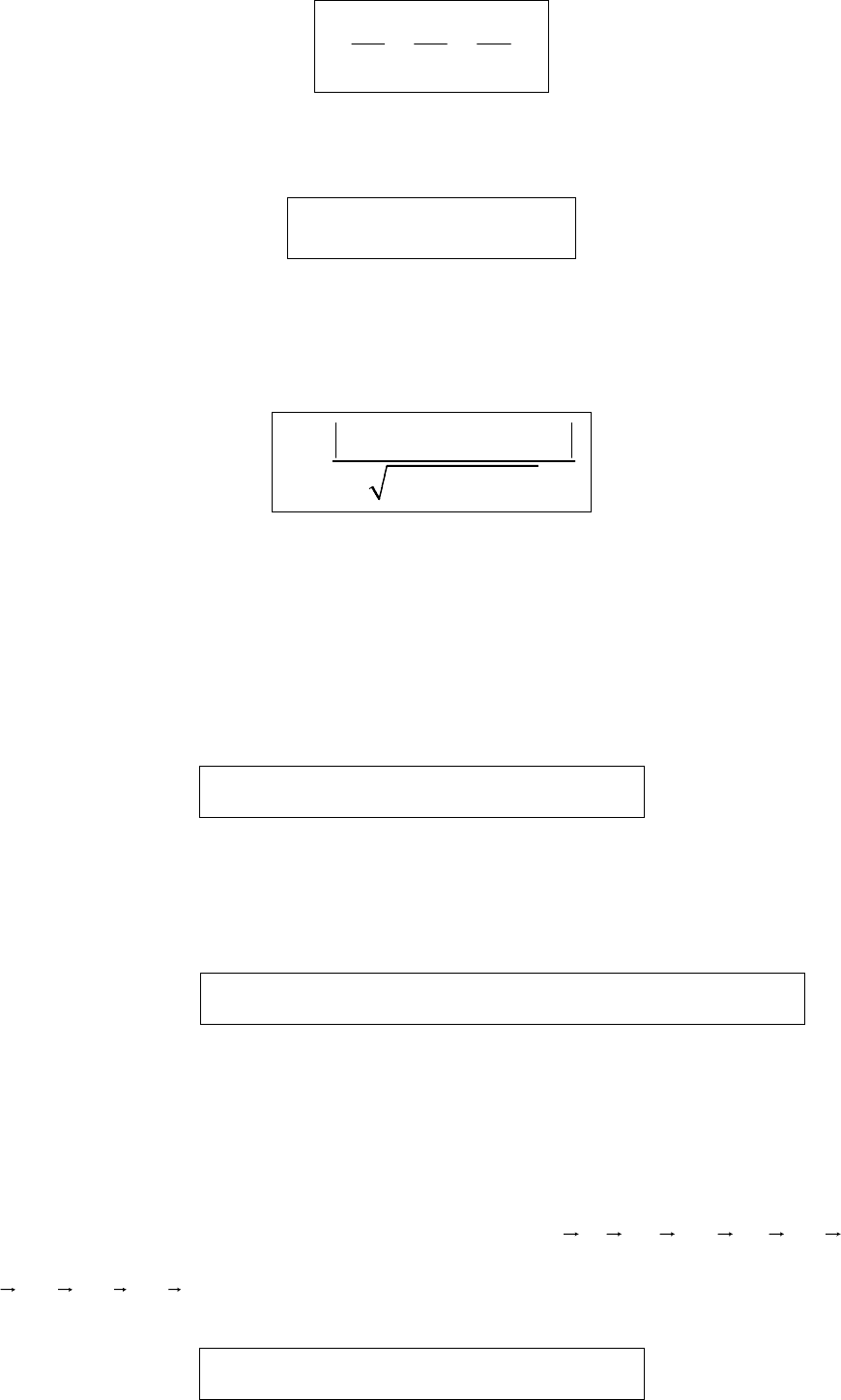
визначається як кут між нормалями до цих площин
за формулою:
1 2 1 2 1 2
2 2 2 2 2 2
1 1 1 2 2 2
cos
A A B B C C
A B C A B C
ϕ
+ +
=
+ + ⋅ + +
.
Звідси умова паралельності двох площин:
90
1 1 1
2 2 2
A B C
A B C
= =
.
Умова перпендикулярності:
1 2 1 2 1 2
0
A A B B C C
+ + =
.
Відстань точки
0 0 0
( , , )
M x y z
від площини
0
Ax By Cz D
+ + + =
визначається за формулою
0 0 0
2 2 2
Ax By Cz D
d
A B C
+ + +
=
+ +
.
Зазначимо, що вираз під знаком модуля буде додатнім, якщо точка
0 0 0
( , , )
M x y z
і початок координат розташовані по різні боки від площини і
від’ємним – якщо по один бік.
Рівняння площини, яка проходить через точку
0 0 0
( , , )
M x y z
і
перпендикулярна до вектора
N Ai Bj Ck
= + +
r
r
r r
має вигляд:
0 0 0
( ) ( ) ( ) 0
A x x B y y C z z
− + − + − =
.
При довільних
, ,
A B C
отримаємо рівняння в’язки площин, що
проходять через точку
0
M
.
Рівняння
1 1 1 1 2 2 2 2
( ) 0
A x B y C z D A x B y C z D
λ
+ + + + + + + =
,
при довільному
λ
задає жмуток площин, що проходять через пряму
перетину площин
1 1 1 1
0
A x B y C z D
+ + + =
і
2 2 2 2
0
A x B y C z D
+ + + =
.
Рівняння площини, яка проходить через три точки
1 1
( )
M r
r
,
2 2
( )
M r
r
,
3 3
( )
M r
r
, де
1 1 1 1
r x i y j z k
= + +
r
r r
r
,
2 2 2 2
r x i y j z k
= + +
r
r r
r
,
3 3 3 3
r x i y j z k
= + +
r
r r
r
,
отримаємо з умови компланарності векторів.
1
rr − ,
1
2
rr − ,
1
3
rr − , де
kzjyixr ++= – радіус-вектор довільної точки
M
шуканої площини:
1 2 3
( )( )( ) 0
r r r r r r
− − − =
r r r r r r
,
