Бораковський О.В. Вища математика: конспект лекцій, модуль І
Подождите немного. Документ загружается.

31
Таким чином =
−
→
2
sin21lim
2
0
x
x
101
2
sinlim21
2
2
0
=−=
−
→
x
x
.
Доведемо першу чудову границю 1
sin
lim
0
=
→
x
x
x
.
Доведення.
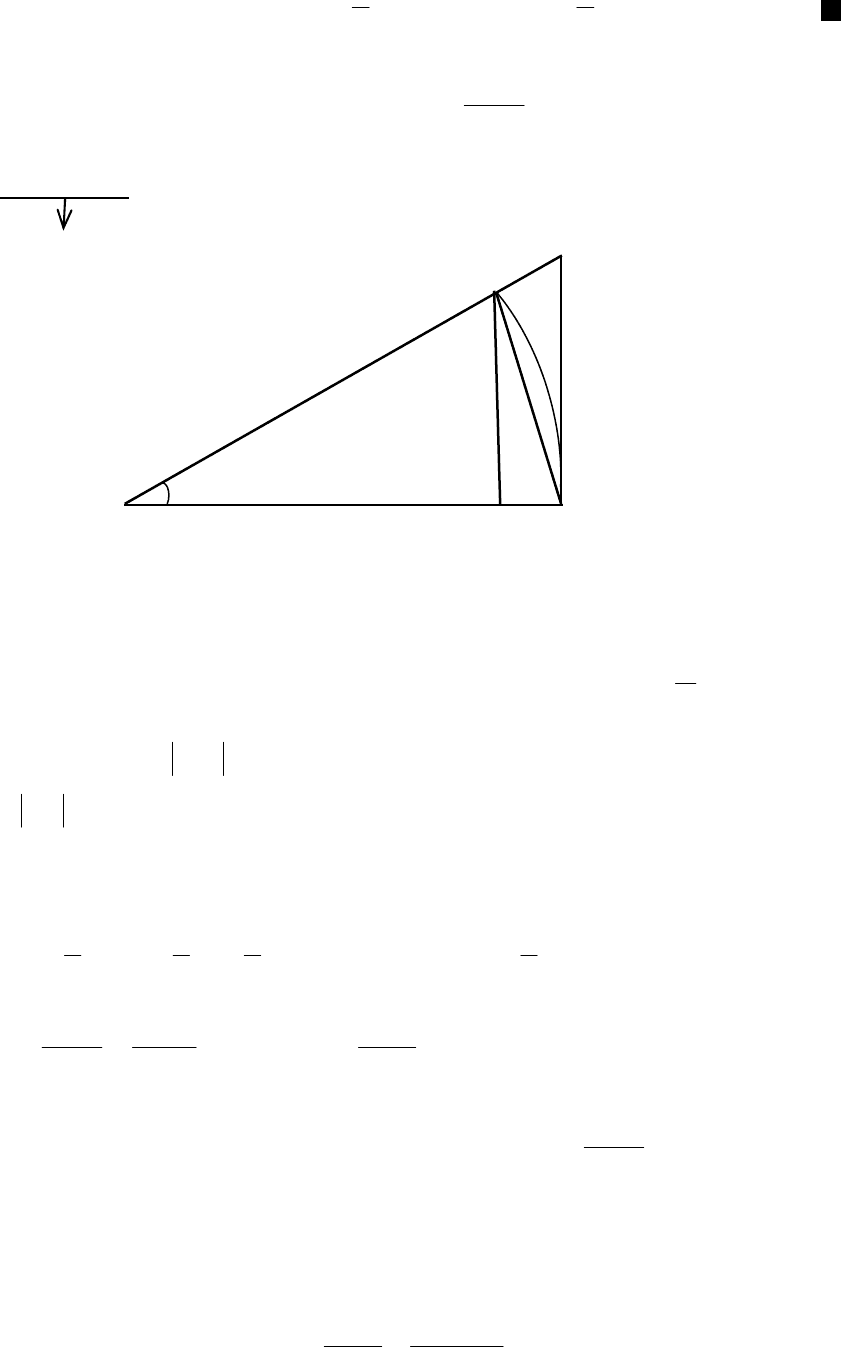
Розглянемо частину кола
радіуса одиниця, рис. 13.
Рис. 13
Позначимо радіальну міру кута
MOB
за
x
. Нехай
2
0
π
<< x .
На малюнку xAM sin
=
, дуга MB чисельно дорівнює центральному
куту x, xtgВС
=
.
Наочно маємо
COBMOBсектораMOB
SSS
∆∆
<
<
.
Тоді
xtgxx
2
1
2
1
sin
2
1
<<
. Поділимо на 0sin
2
1
>x
:
x
x
x
x
cossin
1
<<
або 1
sin
cos
<<
x
x
x
.
Так як 1coslim
0
=
→
x
x
і 11lim
0
=
→
x
, то змінна
x
x
sin
розташована між
двома величинами, які мають одну й ту ж границю, яка дорівнює 1, отже, за
теоремою про стиснуту змінну, маємо 1sinlim
0
=
→
x
x
.
Нехай тепер
0
x
<
. Маємо
x
x
x
x
−
−
=
)(sinsin
, де
0
x
>
−
.
A
B
C
M
tg x
sin x
x
cos x
1
0
32
Звідси 1
sin
lim
)0(
0
=
<
→
x
x
x
x
, а тому 1
sin
lim
0
=
→
x
x
x
.
Для неперервної функції (див. нижче) має місце граничний перехід
=
→→
xfxf
axax
lim)(lim .
Усі елементарні функції неперервні в області визначення. Розглянемо
розкриття невизначеностей наступних видів:
∞
∞
,
0
⋅
∞
,
∞
−
∞
,
0
∞
,
0
0
,
∞
1
.
Приклад. 1
341
432
4
4
432
lim
3
2
1
−=
+−−
−+
=
+
+
−−
−→
x
x
xx
x
.
Після підстановки замість x мінус одиниці, не маючи невизначеностей,
отримаємо відповідь.
Розглянемо
∞
∞
=
∞→
)(
)(
lim
xQ
xP
m
n
x
, де )(xP
n
і )(xQ
m
многочлени порядку n і
m відповідно,
N
n
∈
і
N
m
∈
.
Для розкриття невизначеностей виду
∞
∞
скорочуємо чисельник і
знаменник на старший ступінь x чисельника або знаменника і користуємось
умовною таблицею.
0
0
c
=
⋅
;
∞
=
∞
⋅
c
; 0
c
0
=
;
∞=
∞
c
∞=
0
c
;
0
0
=
∞
; де
с=const.
Приклад.
2
1
2
12
15
2
lim
12
152
lim
222
2
222
2
2
2
==
−+
+−
=
∞
∞
=
−+
+−
∞→∞→
x
x
x
x
x
xx
x
x
x
xx
xx
xx
,
=
=
=
;2
;2
m
mn
n
.
33
Приклад. =
+−
+−
=
∞
∞
=
+−
+−
∞→∞→∞→
33
2
3
3
33
2
3
4
23
24
3
1
3
limlim
3
13
lim
x
x
x
x
x
x
xx
x
x
x
xxx
xx
xxx
,
∞==
∞→
1
lim
x
x
,
=
>
=
;3
;4
m
mn
n
.
Приклад. =
+−
+−
=
∞
∞
=
+−
+−
∞→∞→
22
2
2
3
222
2
23
2
5
2
10
7
lim
52
107
lim
x
x
x
x
x
xx
x
x
x
xx
xx
xx
,
0
2
1
lim =
−
=
∞→
x
x
,
=
<
=
;3
;2
m
mn
n
.
Зазначимо, що при
m
n
=
границя дорівнює відношенню коефіцієнтів
при старших ступенях х у чисельнику і знаменнику. Якщо ж
m
n
<
, – то
нулю;
m
n
>
, – то нескінченості.
Розглянемо обчислення границь від раціональних функцій виду
0
0
)(
)(
lim
0
=
→
xQ
xP
m
n
xx
.
Для розкриття невизначеності такого виду треба зробити алгоритмічні
перетворення у чисельнику і знаменнику метою яких є виділення множника
виду )(
0
xx
−
, що прямує до нуля. Це можна зробити розкладаючи
многочлени на множники, ураховуючи формули:
(
)
22
2
2 bababa +±=± ;
(
)
3223
3
33 babbaaba +±±=± ;
(
)
(
)
bababa −+=±
22
;
(
)
(
)
2233
babababa +±±=± ,
або поділивши многочлени на множник )(
0
xx
−
.
Приклад. =
++−
++−
==
−−
−
→→
)12)(1(
)1)(1(
lim
0
0
12
1
lim
2
2
1
23
3
1
xxx
xxx
xx
x
xx
4
3
1
2
1
lim
2
2
1
=
+
+
++
=
→
x
x
xx
x
.
34
Тут виконали ділення многочлена на двочлен наступним чином:
1
2
23
−
−
х
х
1
−
х
23
2
2
х
х
−
1
2
2
++
х
х
1
2
−
х
х
х
−
2
1
−
х
1
−
х
0.
Для усунення невизначеностей у разі ірраціональних виразів, треба
домножити чисельник і знаменник на спряжений вираз.
Приклад.
0
0
4
22
lim
2
2
=
−
−+
→
x
x
x
.
/Домножимо чисельник і знаменник на 22 ++x , розкладемо
/)2)(2(4
2
−+=− xxx
=
++−+
−+
=
++−+
++−+
→→
)22)(2)(2(
42
lim
)22)(2)(2(
)22)(22(
lim
22
xxx
x
xxx
xx
xx
16
1
)222)(22(
1
lim
)22)(2(
1
lim
22
=
+++
=
+++
=
→→ xx
xx
.
Для розкриття невизначеності виду
∞
−
∞
треба застосувати елементарні
перетворення для зведення їх до невизначеностей виду
∞
∞
або
0
0
.
Приклад.
( )
(
)
(
)
=
++
++−+
=∞−∞=−+
∞→∞→
xx
xxxx
xx
xx
1
11
lim1lim
0
1
1
1
lim =
∞
=
++
−
+
=
∞→
xx
xx
x
.
Розглянемо приклади обчислення границь за допомогою першої і
другої чудових границь і порівняння нескінченно малих.
Приклад.
k
kx
kx
k
kx
kxk
x
kx
xxx
===
→→→
sin
lim
sin
lim
sin
lim
000
.
Тут використали першу чудову границю.
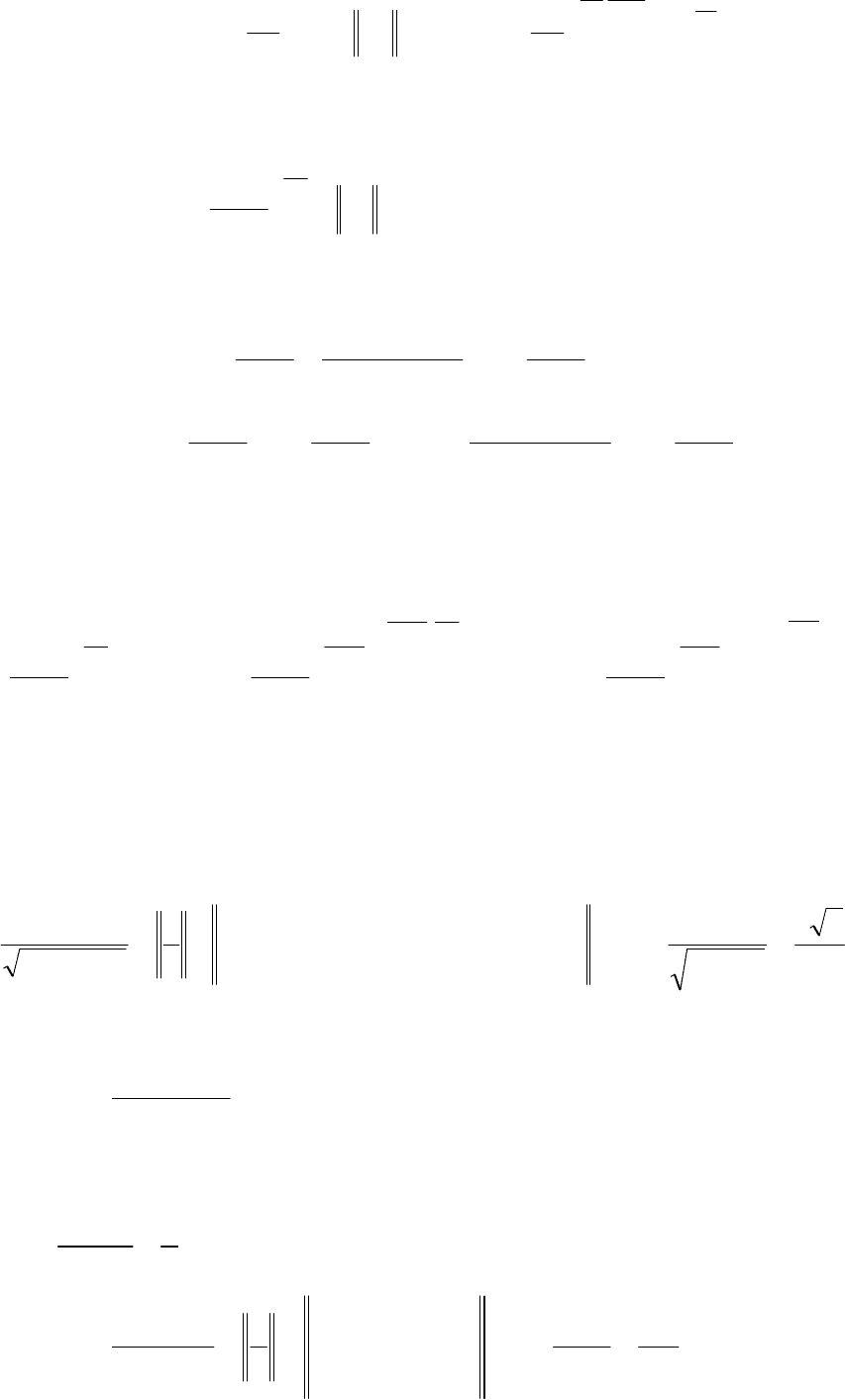
35
Приклад.
3
10
x3
x25
5
x3
x
x2
x
e
x3
5
1lim1
x3
5
1lim =
+==
+
⋅
⋅
∞→
∞
∞→
Тут використали другу чудову границю.
Приклад.
∞
∞→
=
−
+
1
2
4
lim
2
5x
x
x
x
.
Спочатку виділимо цілу частку:
2
6
1
2
422
2
4
−
+=
−
+
+
−
=
−
+
x
x
x
x
x
Або так:
2
6
1
2
24
11
2
4
1
2
4
−
+=
−
+
−
+
+=−
−
+
+=
−
+
x
x
xx
x
x
x
x
.
Тепер треба виділити у показнику ступеня вираз, обернений до
дробової частини:
=
−
+=
−
+
⋅
−
⋅
−
∞→∞→
2
5
2
6
6
2
2
5
2
6
1lim
2
4
lim
x
x
x
x
x
x
xx
x
15
6
2
2
15
lim
2
6
1lim e
x
x
x
x
x
=
−
+
∞→
⋅
−
∞→
Границя виразу у квадратних дужках дає число
e
, а границя степеня
дорівнює 15.
Приклад.
( )
4
23
22
3
lim
222~2sin24cos1
0,3~3
0
0
4cos1
3
lim
2
0
2
0
==
⋅⋅=−
→
==
−
→→
x
x
xxxx
xxxtg
x
xtg
xx
Тут і далі скористалися еквівалентними нескінченно малими величинами.
Приклад.
2
0
1 cos 2
lim
sin3
x
x
x x
→
−
.
(
)
.0,3~3sin,2~2sin2cos1
2
22
→⋅=− xxxxxxxx
Тоді
0
2 2 4
lim
3 3
x
x x
x x
→
⋅
=
⋅
.
Приклад.
0
0 0
0
3 1 ~ ln3
3 1 0 ln3 ln3
lim lim
2 0 2 2
~ 2
x
x
x
x x
x
x
x
arcsin x x
arcsin2x x
→
→ →
→
−
−
= = = = .
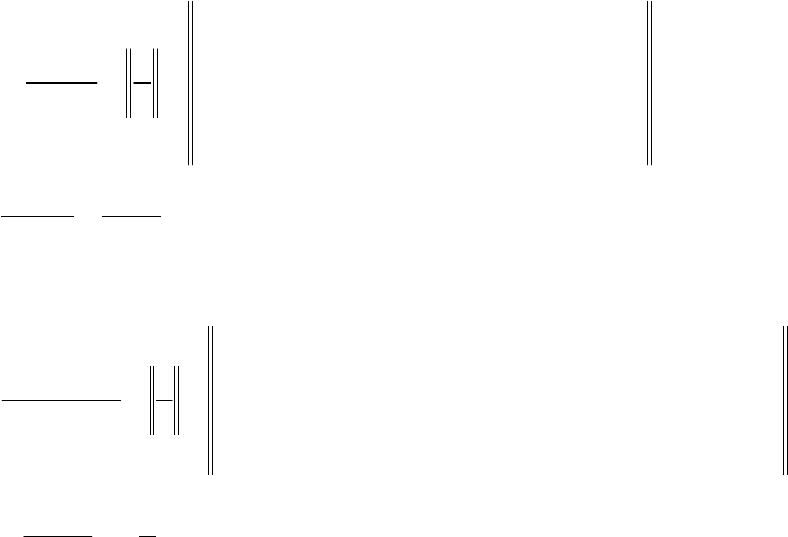
36
Приклад.
2 2 2 2
2 0
( 2) 0
0
2 , 0 2
2 4 0
lim 2 4 2 2 2 (2 1) 2 ln 2
sin 0
2 ) sin
x
x z z
x z
x
z
x z z x z
~ z
x
sin x sin( z z ~ z
π
π π π π π
+
→ →
− →
→
− = → ⇒ = +
−
= = − = − = − =
= + =
ππ
2ln42ln4
lim
0
=
→
z
z
z
.
Приклад.
( )
( )
( )
( )( )
( ) ( )
.
3
2
3
2
lim
0,3~1ln31ln
2~sin2~sin21ln2cosln
sin212cos112cos112cos
0
0
1ln
2cosln
lim
2
2
0
22
3
2
22
2
3
20
−=
−
=
=
→+=+
−−−+=
−=−−=+−=
==
+
→
→
x
x
xxxx
xxxx
xxxx
x
x
x
x
Обчислення інших границь розглянемо нижче у розділі правило Лопіталя.
3. Неперервність функції
Функція
)
(
x
f
має назву неперервної у точці а, якщо: 1) вона визначена
у деякому околі точки а; 2) існує границя )(lim xf
ax→
; 3) ця границя дорівнює
значенню функції у точці а, тобто )()(lim afxf
ax
=
→
.
Існує інше визначення неперервності функції. Функція
)
(
x
f
називається неперервною у точці а, тоді і тільки тоді, коли у цій точці
нескінченно малому приросту аргумента відповідає нескінченно малий
приріст функції: 0xf
ax
=
→
)(lim
∆
, де
)
(
)
(
a
f
x
f
f
−
=
∆
,
a
x
x
−
=
∆
.
Функція
)
(
x
f
неперервна у деякій області (інтервалі, сегменті, тощо)
якщо вона неперервна у кожній точці цієї області.
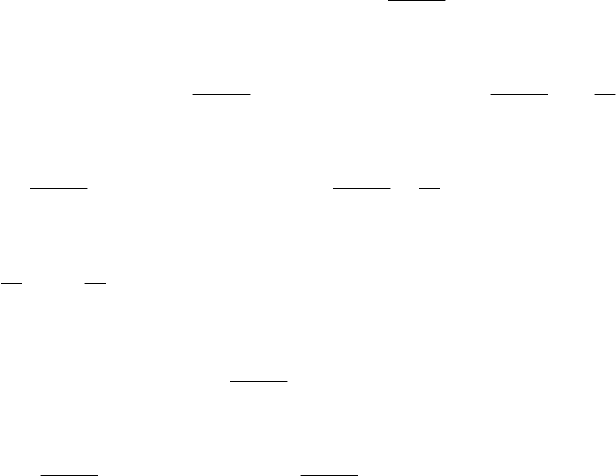
37
Точка а, що належить області визначення функції, включаючи
границю, має назву точки розриву, якщо у цій точці не виконуються умови
неперервності функції.
Якщо існують скінченні границі )()(lim 0afxf
0ax
−
=
−→
та
)()(lim 0afxf
0ax
+
=
+→
, причому не усі три числа
)
(
a
f
,
)
(
0
a
f
−
,
)
(
0
a
f
+
дорівнюють одне одному, то точка а – точка розриву першого роду.
Точки розриву першого роду поділяються на точки усувного розриву,
коли
)
0
(
−
a
f
)
0
(
+
=
a
f
)
(
a
f
≠
і точки стрибка, коли
)
0
(
−
a
f
)
0
(
+
≠
a
f
.
Різниця
)
0
(
+
a
f
)
0
(
−
−
a
f
має назву стрибка функції
)
(
x
f
у точці а.
Точками розриву другого роду називають точки розриву, що не є
точками розриву першого роду. У точках розриву другого роду не існує хоча
б одна з односторонніх границь.
Сума і добуток скінченого числа неперервних функцій є неперервною
функцією.
Частка двох неперервних функцій є неперервна функція у тих точках,
де дільник не дорівнює нулю.
Приклад. Дослідити на розрив функцію
5
1
−
=
x
arctgy .
Розв’язання. Якщо
0
5
−
→
x
, то −∞→
−
5
1
x
,
2
5
1
lim
05
π
−=
−
−→
x
arctg
x
.
Якщо
0
5
+
→
x
, то ∞→
−
5
1
x
,
2
5
1
lim
05
π
=
−
+→
x
arctg
x
.
Стрибок функції
π
ππ
=
−−
22
.
5
=
x
– точка розриву першого роду.
Приклад. Показати, що функція
5
−
=
x
x
y має розрив при
5
=
x
.
Розв’язання. −∞=
−
−→
5
lim
05
x
x
x
; +∞=
−
+→
5
lim
05
x
x
x
, тобто скінченних
границь немає. Тоді
5
=
x
– точка розриву другого роду.
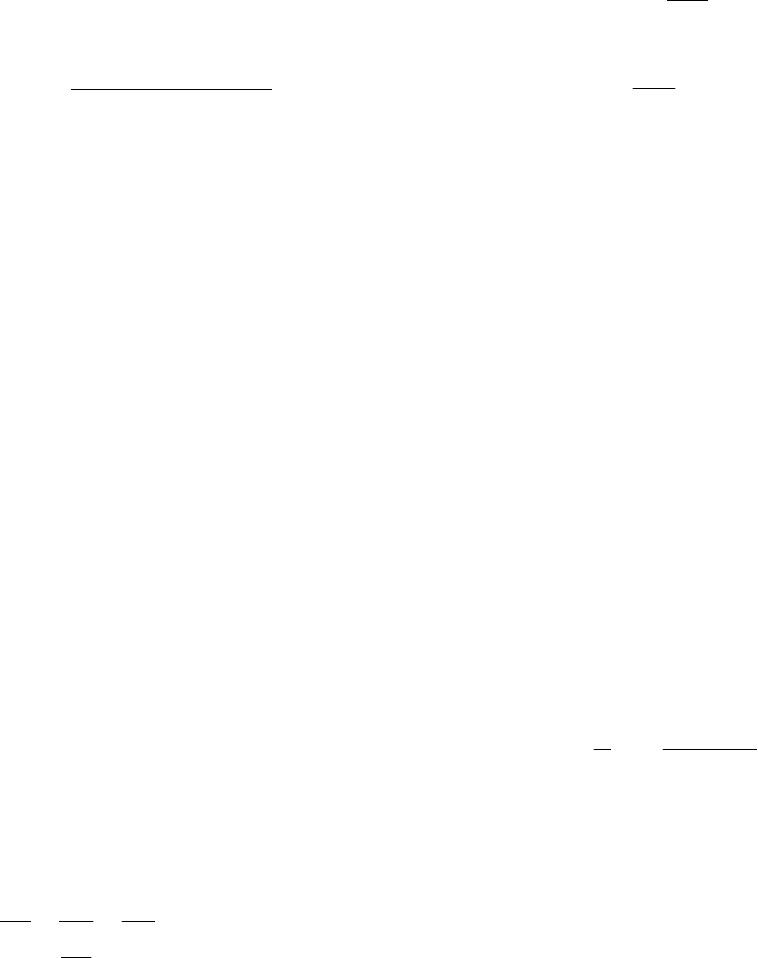
38
4. Похідна
Розглянемо функцію
)
(
x
f
y
=
. Нехай
1
x та
2
x – значення аргументу, а
)(
1
1
xfy
=
та )(
2
2
xfy
=
відповідні значення функції
)
(
x
f
y
=
. Різниця
1
2
xxx
−
=
∆
– приріст аргументу, а різниця
1
2
yyy
−
=
∆
– приріст функції
на відрізку
[
]
2
1
xx ; .
Похідною від функції
)
(
x
f
y
=
по аргументу
x
називається граничне
відношення приросту функції до приросту аргументу, коли приріст
аргументу прямує до нуля:
x
y
y
x
∆
∆
∆
0
lim'
→
= , або
x
xfxxf
xf
x
∆
∆
∆
)()(
lim)('
0
−
+
=
→
. Похідну позначають також
xd
yd
.
Поняття похідної використовують у багатьох галузях науки, особливо
при вивченні швидкості перебігу різних процесів. Якщо функція
)
(
x
f
y
=
описує закон руху матеріальної точки, то похідна визначає швидкість цієї
точки у даний момент часу. Взагалі похідна це швидкість зміни функції у
точках.
З геометричної точки зору похідна представляє кутовий коефіцієнт
дотичної до графіка функції
)
(
x
f
y
=
у точці
x
.
Пошук похідної має назву диференціювання функції.
Основні правила диференціювання
.
Нехай
с
– стала,
)
(
x
u
u
=
,
)
(
x
v
v
=
– функції, що мають похідні, тоді:
1)
0
c
=
'
; 2)
1
x
=
'
;
3)
vuvu
′
±
′
=
′
±
)( ;
4)
uccu
′
=
′
)( ; 5)
vuvuuv
′
+
′
=
)'( ;
6)
2
v
vuvu
v
u
′
−
′
=
′
;
7) якщо
)
(
u
f
y
=
, а
)
(
x
u
u
=
, тобто
[
]
)(
xufy
=
, то
x
u
x
yyy
'''
⋅
=
– це правило
диференціювання складної функції;
8)
y
x
x
dy
dx
dx
dy
y
′
===
′
11
– правило диференціювання оберненої функції.
39
Приклад. Спираючись на визначення похідної знайти похідну від
2
xy = .
Розв’язання. Надамо приріст аргументу
x
∆
. Знайдемо приріст функції
222222
)(2)(2)( xxxxxxxxxxy
∆∆∆∆∆∆
+=−+++=−+= . Знайдемо
границю відношення
x
y
∆
∆
при
0
x
→
∆
.
xxx
x
xxx
x
y
xxx
2)2(lim
)(2
limlim
0
2
00
==
+
=
→→→
∆
∆
∆∆
∆
∆
∆∆∆
.
Таким чином xx 2)'(
2
= . Аналогічно отримують похідні від інших
елементарних функцій. Нижче подано таблицю похідних для функції
)
(
x
u
u
=
.
1)
0
c
=
′
11)
( )
u
u
u
′
⋅=
′
2
cos
1
tg
2)
unuu
1nn
′
⋅=
′
−
)(
12)
( )
u
u
u
′
⋅−=
′
2
sin
1
ctg
3)
(
)
u2
u
u
′
=
′
13)
( )
2
1
arcsin
u
u
u
−
′
=
′
4)
2
u
u
u
1
′
−=
′
14)
( )
2
1
arccos
u
u
u
−
′
−=
′
5)
( )
a
u
u
u
a
ln
log
′
=
′
15)
( )
2
1
arctg
u
u
u
+
′
=
′
6)
( )
u
u
u
′
=
′
ln
16)
( )
2
1
arcctg
u
u
u
+
′
−=
′
7)
(
)
uaaa
uu
′
⋅=
′
ln
17)
( )
'uu
2
ee
u
uu
'
⋅=
−
=
−
chsh
8)
(
)
uee
uu
′
=
′
18)
( )
'shch
'
uu
2
ee
u
uu
⋅=
−
=
−
9)
( )
uuu
′
⋅=
′
cossin
19)
( )
'u
uu
1
u
u
u
'
⋅
⋅
=
′
=
shch
sh
th
10)
( )
uuu
′
⋅−=
′
sincos
20)
( )
'u
uu
1
u
u
u
'
'
⋅
⋅
−=
=
shch
sh
cth

40
Розглянемо приклади.
Приклад. Знайти похідну
x
y
sin
ln
=
.
Розв’язання. Маємо
u
y
ln
=
, де
x
u
sin
=
;
( ) ( )
==⋅=
''
sin
sin
'ln x
x
1
u
u
1
u
=
x
x
sin
cos
=
x
ctg
.
Приклад. Знайти похідну
2
2
x
2
x
y
−= cossin .
Розв’язання
. =
−⋅
−=
'
2
cos
2
sin
2
cos
2
sin2'
xxxx
y ⋅
−
2
x
2
x
2 cossin
=
⋅+⋅⋅
2
1
2
sin
2
1
2
cos
xx
x
xx
cos
2
cos
2
sin
22
−=− .
Для знаходження функції, що задана неявно
0
)
,
(
=
y
x
f
необхідно
продиференціювати обидві частини цієї рівності, ураховуючи правило
диференціювання складеної функції. Потім розв’язуємо рівняння першого
ступеня відносно
'
y
.
Приклад.
Знайти похідну
0ln
2
=− yxy .
Розв’язання. Диференціюємо обидві частини цієї рівності
0
'
'21
2
=−+⋅
y
y
yyxy ; звідси
2
3
2
2
2112
'
xy
y
xy
yy
y
−
=
−
⋅
−= .
Якщо функція аргументу
x
задана у параметричній формі
)
t
(
x
ϕ
=
,
)
(
t
y
ψ
=
, то
dt
dx
dt
dy
dx
dy
= , або .
Приклад. Знайти похідну
x
y' якщо
t
a
x
cos
=
,
t
a
y
sin
=
.
Розв’язання.
tctg
ta
ta
x
y
y
t
t
x
−=
−
==
sin
cos
'
'
' .
Звільняючись від параметра
t
маємо
y
x
ya
ax
t
t
y
x
−=
⋅
⋅
−=
−
=
sin
cos
'
.
t
t
t
x
y
y
'
'
' =
