Бондарев В.П. Концепции современного естествознания
Подождите немного. Документ загружается.


математические модели, детально описывающие систему в целом, поскольку параметры
порядка отражают содержание оснований неравновесной системы. Поэтому выявление
параметров порядка - одна из важнейших задач, решаемых при изучении
самоорганизующихся систем.
§ 11.3. Закономерности самоорганизации и эволюционного процесса
Закономерности и факторы эволюции
Одной из центральных в синергетике является идея о принципиальной возможности
спонтанного возникновения порядка и организации из беспорядка и хаоса в результате
процесса самоорганизации. Решающим фактором самоорганизации выступает
положительная обратная связь системы и среды. При этом система начинает
самоорганизовываться и противостоит тенденции ее разрушения средой (в химии такое
явление называется автокатализом).
Способность систем к самоорганизации во многом определяется характером
взаимодействия случайных и необходимых факторов системы и ее среды. Обычно
самоорганизация переживает переломные моменты - точки бифуркации. При этом под
бифуркацией обычно понимают приобретение нового качества в движениях
динамической системы при малом изменении ее параметров. Основы теории бифуркации
заложены А. Пуанкаре и A.M. Ляпуновым в начале XX в., затем эта теория была развита
A.A. Андроновым и его учениками.
Вблизи точек бифуркации в системах наблюдаются существенные случайные
отклонения физических величин от их средних значений (флуктуации), поэтому роль
случайных факторов резко возрастает. В переломный момент самоорганизации
принципиально неизвестно, в каком направлении будет происходить дальнейшее развитие:
станет ли состояние системы хаотическим или она перейдет на новый, более высокий
уровень упорядоченности и организации (фазовые переходы и диссипативные структуры -
лазерные пучки, неустойчивости плазмы, химические волны Белоусова - Жаботинского,
структуры Рэлея и др.). В точке бифуркации система как бы стоит перед выбором пути
дальнейшего развития. В таком состоянии небольшая флуктуация может послужить
толчком к началу эволюции (организации) системы в некотором определенном (часто
неожиданном или даже маловероятном) направлении, одновременно исключая
возможности развития в других направлениях. Оказалось, что переход от хаоса к порядку
поддается математическому моделированию и существует не так уж много общих моделей
такого перехода. При этом существенно, что качественные переходы в самых разных
сферах действительности (в природе и обществе) могут происходить по одному и тому же
сценарию. Знание основных бифуркаций позволяет существенно облегчить исследование
реальных систем (физических, химических, биологических и др.), в частности предсказать
характер новых движений, возникающих в момент перехода системы в качественно другое
состояние, оценить их устойчивость и область существования.
Итак, основными условиями формирования новых структур являются открытость
системы, нахождение ее вдали от точки равновесия и наличие флуктуации.
Неустойчивость и неравновесность определяют развитие систем. В особой точке
бифуркации (критическое состояние) флуктуации достигают такой силы, что организация
системы может разрушиться. Разрешение кризисной ситуации достигается быстрым
переходом диссипативной системы на новый, более высокий уровень упорядоченности,
который получил название диссипативной структуры. Это и есть акт самоорганизации
системы. Поскольку флуктуации случайны, то и выбор конечного состояния системы
является случайным, неоднозначным, причем процесс перехода одноразовый и
необратимый. В процессе перехода все элементы системы ведут себя коррелированно
(согласованно), хотя до этого они находились в состоянии хаоса.
Общая схема эволюционного процесса как последовательности процессов

самоорганизации сводится к следующему [29]:
◊ относительно стабильное п-е состояние системы утрачивает устойчивость. В качестве
причин, вызывающих потерю устойчивости, выступают временные изменения
внутреннего состояния или наложенных краевых условий. Наиболее характерной
причиной эволюционной неустойчивости является внезапное появление новой моды в
движении, новой разновидности молекул в химии, нового вида в биологии. Этот новый
элемент в рассматриваемой динамической системе приводит к потере устойчивости
состояния системы, которое до появления нового элемента было устойчивым;
◊ неустойчивость, обусловленная новым элементом в системе, запускает динамический
процесс, который приводит к дальнейшей самоорганизации системы, и система порождает
новые упорядоченные структуры;
◊ по завершении процесса самоорганизации система переходит в эволюционное
состояние (п +1). После n-го эволюционного цикла начинается новый (п +1)-й
эволюционный цикл.
Характерно, что реальная эволюция никогда не заканчивается, она каким-то образом
находит выход из любого тупика, и этим выходом является новый цикл самоорганизации.
Каждый парциальный (частный) эволюционный процесс
переводит систему в новую, в определенном смысле
более высокую эволюционную плоскость, а процесс в
целом обладает спиральной структурой (рис. 11.3).
Анализ действующих и определяющих
последовательность состояний системы условий, сил и
механизмов необходим для разработки теории
эволюции. Окончательные ответы пока получить не
удается.
Особое значение придается следующим факторам [29]:
◊ способности к уменьшению энтропии путем обмена энергией и веществом с
окружающей средой;
◊ неравновесному характеру системы, находящемуся на закритическом расстоянии от
термодинамического равновесия;
◊ нелинейности (динамика системы существенно определяется эффектами, которые
описываются уравнениями второго и более высокого порядка);
◊ способности к самовоспроизведению, т.е. к образованию относительно точных копий
исходной системы или подсистем;
◊ конечности времени жизни системы, связанной с ней непрестанной смене поколений
и процессу обновления;
◊ существованию нескольких устойчивых состояний системы, зависимости текущего
состояния от предыстории, потенциальной способности к хранению информации;
◊ отбору систем и механизмов с благоприятными свойствами из большого числа
возможных конкурентных процессов;
◊ стабильности системы при случайной ошибке в процессе репродукции как источнику
новых структур, механизмов и информации;
◊ обработке информации, т.е. способности к ее созданию, хранению, воспроизведению
и использованию;
◊ оптимизации и адаптации, способности подстраиваться к изменяющимся внешним
условиям, существованию критериев оптимизации;
◊ морфогенезу, т.е. формообразованию системы и ее органов;
◊ образованию эталонов с тенденцией к увеличению многообразия и сложности;
◊ ветвлению, т.е. все более сильному расщеплению реального и в еще большей мере
потенциального пути эволюции;
◊ сетевой структуре с тенденцией к образованию все более сложных соотношений и
зависимостей между подсистемами;
◊ единству действия необходимых и случайных факторов;
◊ дифференциации, специализации и распределению функций подсистем;
◊ объединению систем путем соединения в целое все более возрастающей сложности и
все большей потенции к действию;
◊ иерархическому строению систем, элементы которых вложены один в другой
(существование параметров порядка);
◊ ускорению эволюции, т.е. постоянному нарастанию средней скорости эволюционного
процесса вследствие механизмов обратной связи.
Этот перечень можно легко продолжить.
Особенности эволюционного процесса
Одна из существенных черт глобальной эволюции - подобие явлений в системах, на
первый взгляд совершенно различных. Например, обнаружена аналогия качественных
переходов при эволюционных процессах с фазовыми переходами в термодинамике.
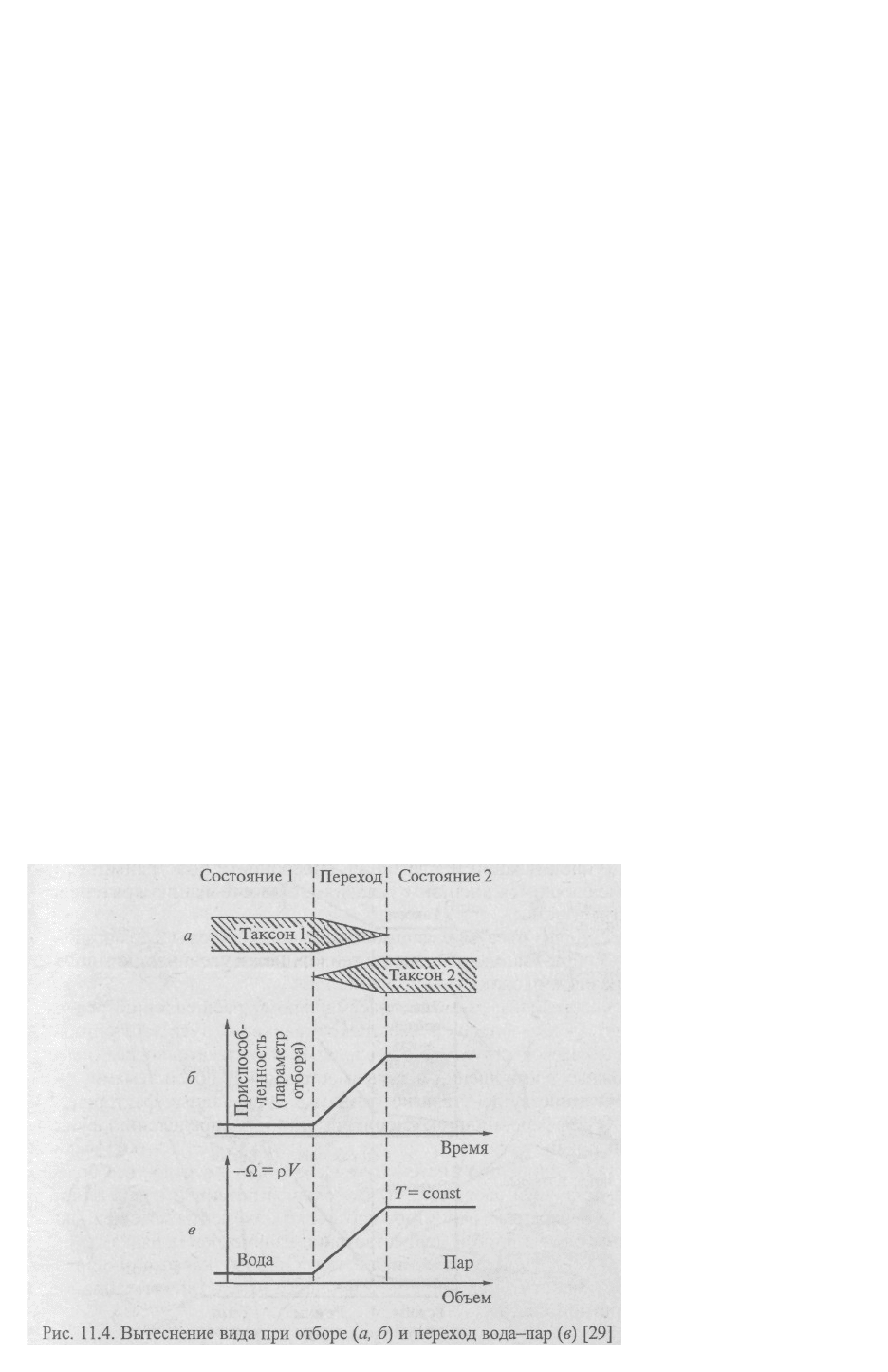
Проиллюстрировать это положение можно на примерах из физики и экологии (рис. 11.4 и
11.5). Пусть биологические виды занимают на определенной территории одну
экологическую нишу. При появлении нового вида, который существенно лучше
использует ту же нишу, наступает фаза перехода от сосуществования к полному
вытеснению исходных видов (рис. 11.4, а, б). Отметим общие свойства такого рода
процессов: состояния 1 и 2 разделены переходной областью конечной величины; в
переходной области состояния (виды) отличимы друг от друга; симметрия относительно
использования видами экологической ниши не должна нарушаться; скачкообразный
переход может быть обойден, например, с помощью медленного улучшения селекционной
ценности таксона 1 до ценности таксона 2. Аналогичными свойствами характеризуется и
такой, например, термодинамический фазовый переход, как переход вода - пар. На рис.
11.4, в для сравнения представлен график изменения термодинамического потенциала -Ω =
pV функции объема.
Другой существенный для эволюции процесс - специализация, дифференциация или
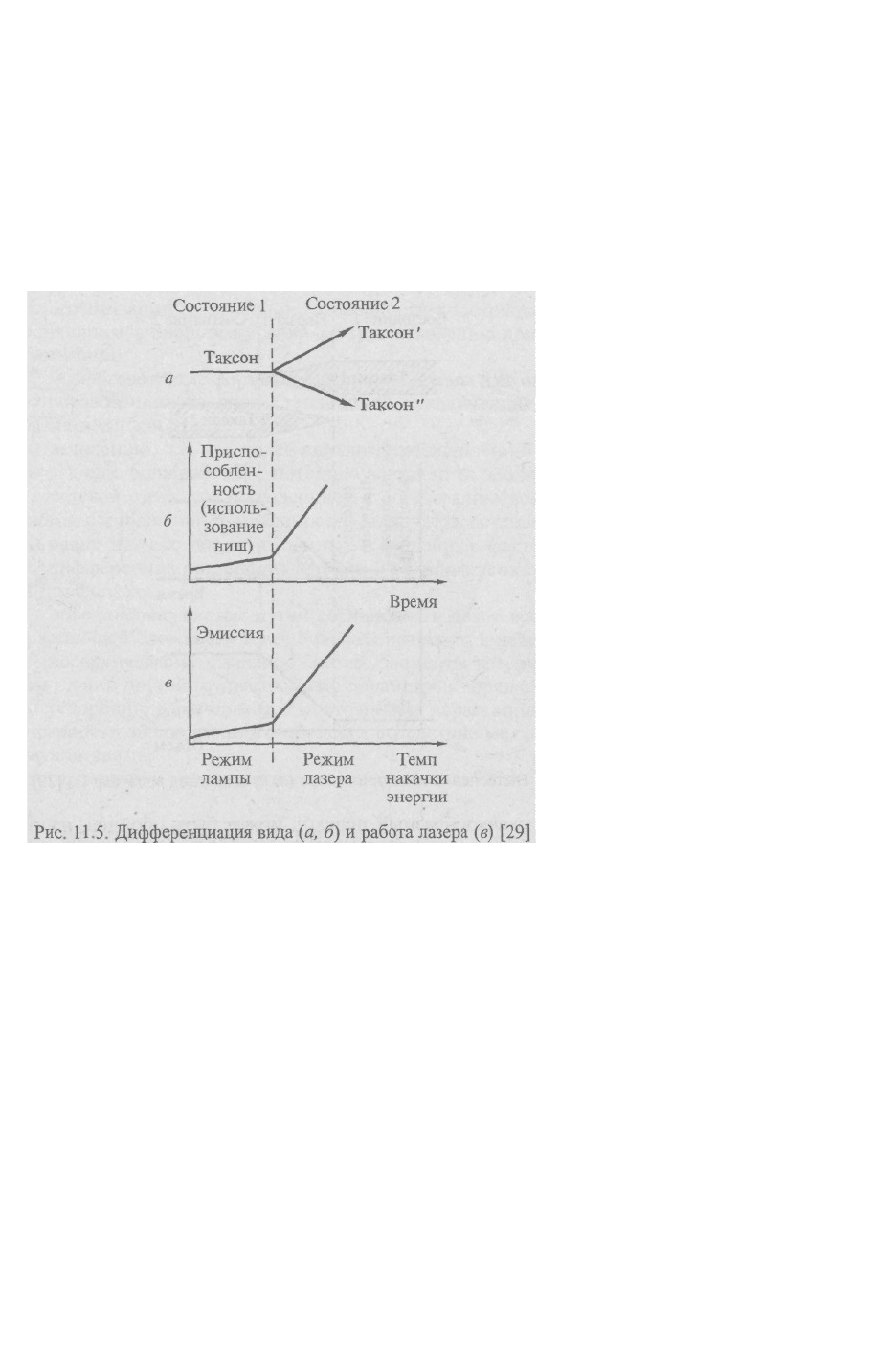
распределение функций (рис. 11.5, а). Например, такой процесс реализуется, когда один
вид использует две экологические ниши, но в ходе эволюции одна часть вида
специализируется по отношению к одной нише, Другая часть - к другой, пока не
образуются два различных вида. Поскольку при этом ресурсы обеих ниш используются с
разделением функций, становится возможным быстрое улучшение приспособленности
(рис. 11.5, б). В подобных случаях удается установить следующие свойства: переход
происходит в определенной точке, отмечаемой прекращением образования смешанного
потомства; с наступлением перехода нарушается симметрия использования ниш
подвидами; в точке перехода оба состояния совпадают. Такой переход аналогичен
кинетическому переходу, например, как в лазере (рис. 11.5, в).
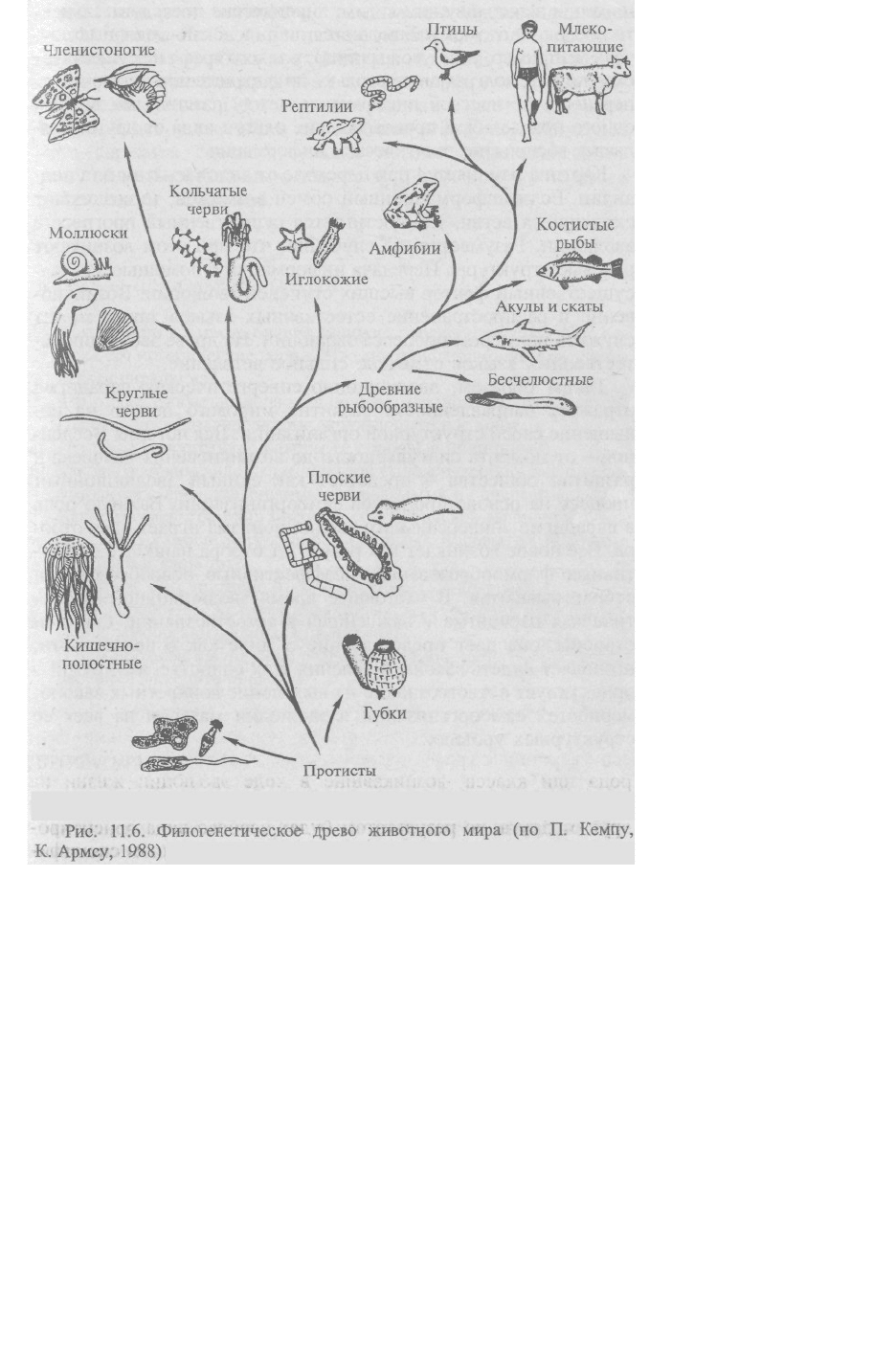
Обратимся к рис. 11.6. На нем отмечена еще одна существенная особенность процессов
эволюции - ветвление. Наглядное описание этого свойства дает теория графов. Например,
если вершинам графа поставить в соответствие виды некоего рода или класса,
возникавшие в ходе эволюции жизни на Земле, и соединить ребрами (стрелками) виды,
произошедшие друг от друга, то результатом будет особого вида ориентированный граф -
древо эволюции. Оно обладает рядом специфических свойств: у такого древа всегда одно
начало и в большинстве случаев несколько концов, соответствующих вымершим или ныне
живущим видам; циклические последовательности предок — потомок наблюдаются лишь
в исключительных случаях (например, у вирусов гриппа); у такого графа не существует
сходящихся подграфов, поскольку по определению исключается перенос генетической
информации между различными видами одного поколения, а происхождение одного вида
от другого означает восприятие генетической информации.
Картина изменяется при переходе от видов к расам или подвидам. Если
информационный обмен возможен, то возникают сходящиеся ветви, т.е. достигается
существенный прогресс в эволюции. Разумеется, не случайно, что при этом возникают
речевые структуры. Передача информации с помощью языка -существенный фактор
высших ступеней эволюции. Возникновение и распространение естественных языков
также может служить примером процесса эволюции. На древе эволюции естественных
языков отмечено сильное ветвление.
Таким образом, эволюционно-синергетическая парадигма отражает направленность
развития мирового целого на повышение своей структурной организации. Вся история
Вселенной - от момента сингулярности до возникновения человека и развития общества
— предстает как единый эволюционный процесс на основе процессов самоорганизации.
Важную роль в парадигме универсального эволюционизма играет идея отбора. Все новое
возникает как результат отбора наиболее эффективных формообразований,
неэффективные новообразования отбраковываются. В настоящее время эволюционно-
синергетическая парадигма - важнейшая в естествознании. С одной стороны, она дает
представление о мире как о целостности, позволяет видеть законы и явления в их
единстве, а с другой - ориентирует естествознание на выявление конкретных
закономерностей самоорганизации и эволюции материи на всех ее структурных уровнях.
В заключение заметим, что в мир далеко еще не познан. Многие явления природы не
получили научного объяснения и потому носят загадочный, таинственный характер. Так,
не исследованы в достаточной мере явления в различных оболочках Земли (литосфере,
атмосфере и т.д.), законы макроэволюции и многое другое. Но было бы наивно полагать,
что естествознание может сразу решить все проблемы познания. Естествознание — не
завершенное здание, а целенаправленная деятельность человечества. Поэтому можно
полагать, что непознанное сегодня будет исследовано и объяснено в будущем, когда для
этого сложатся соответствующие предпосылки. Однако на смену одним непознанным

вопросам придут другие, не менее интересные и загадочные.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Какое место в естествознании занимает эволюционное учение? Каковы его
исторические корни? Что такое эволюционно-синергетическая парадигма?
2. Что такое глобальный эволюционизм и в чем он проявляется? Перечислите фазы
эволюции окружающего нас мира.
1. Что такое синергетика? Каковы ее основные принципы?
3. Каковы основные идеи классической термодинамики? Как они соотносятся с
представлениями, развиваемыми в синергетике?
5. Какие примеры самоорганизующихся процессов вы знаете?
6. Что такое самоорганизующиеся системы? Каковы их основные признаки и
свойства?
7. Что такое диссипативность и нелинейность системы?
8. Каковы основные условия и факторы возникновения и существования
самоорганизующихся процессов?
9. В чем проявляется подобие различных самоорганизующихся процессов? Приведите
примеры.
ЛИТЕРАТУРА
1. Балбоянц А. Молекулы, динамика, жизнь. Введение в самоорганизацию материи.
М., 1990.
2. Винер Н. Кибернетика и общество. М., 1958.
3. Волькенштейн М.В. Энтропия и информация. М., 1980.
2. Грядовой Д.И. Концепции современного естествознания. Структурный курс.
2. Жизнь Земли. Синергетика. Экология. Геодинамика. Музееведение: Сб. науч. тр.
М., 2001.
4. Капица С.П., Курдюмов С/7., Малинецкий Г.Г. Синергетика и прогнозы будущего.
М., 1998.
7. Климентович Н.Ю. Без формул о синергетике. Минск, 1986.
8. Князева E.H. Одиссея научного разума. М., 1995.
8. Князева E.H., Курдюмов С.П. Законы эволюции и самоорганизации сложных
систем. М., 1994.
10. Концепция самоорганизации в исторической ретроспективе. М., 1994.
11. Курдюмов С.П. Законы эволюции и самоорганизации сложных систем. М., 1990.
12. Лопушанская А.И. Термодинамика необратимых процессов. М., 1987.
13. Лоскутов А.Ю., Михайлов A.C. Введение в синергетику. М., 1990.
14. Мелик-Гайказян И.В. Информация и самоорганизация (методологический анализ).
Томск, 1995.
15. Николис Г., Пригожий И. Познание сложного. М., 1990.
16. Осипов А.И. Самоорганизация и хаос: Очерк неравновесной термодинамики. М.,
1986.
17. Пригожин И. От существующего к возникающему: время и сложность в
физических науках. М., 1985.
18. Пригожин И., Стенгерс И. Порядок из хаоса. М., 1986.
19. Степин B.C. Философская антропология и философия науки. М., 1992.
20. Степин B.C. Теоретическое знание. М., 2000.
21. Ферстер Г. фон, Зопф Г.В. Принципы самоорганизации. М., 1964.
22. Хаазе Р. Термодинамика необратимых процессов. М., 1967.
23. Хакен Г. Информация и самоорганизация. Макроскопический подход к сложным
системам. М., 1991.
24. Хакен Г. Синергетика. М., 1985.

25. ЧернавскийД.С. Синергетика и информация. М., 2001.
26. Шеннон К., Бандвагон Е. Работы по теории информации и кибернетике. М., 1963.
27. Щербаков A.C. Самоорганизация материи в неживой природе. М., 1990.
28. Эбелинг В. Образование структур при необратимых процессах. М., 1979.
29. Эбелинг В., Энгель А., Файстель Р. Физика процессов эволюции. М., 2001.
30. Эгейн М. Самоорганизация материи и биологических макромолекул. М., 1973.
31. Эгейн М., Винклер Р. Игра жизни. М., 1979.
32. Эткинс П. Порядок и беспорядок в природе. М., 1987.
