Biringen S., Chow C.-Y. An Introduction to Computational Fluid Mechanics by Example

Подождите немного. Документ загружается.

282 NUMERICAL SOLUTION OF THE INCOMPRESSIBLE NAVIER-STOKES EQUATION

Equation (4.6.9) is the vorticity transport equation, in which the vorticity and the

velocity vectors are the unknowns. In two-dimensional ﬂows the only nonzero

component of the vorticity is along the z direction, so that equation (4.6.9) is

written only for the z component of the vorticity, ω

∂ω

∂t

∂ω

∂x

∂ω

∂y

= ν∇

ω (4.6.10)

The velocities can be written in terms of the stream function

u =

∂ψ

∂y

, v =−

∂ψ

∂x

(4.6.11)

The substitution of (4.6.11) into the deﬁnition of vorticity, ω = ∂v/∂x − ∂u/∂y,

yields the elliptic stream function equation,

∇

ψ =−ω (4.6.12)

The system of equations (4.6.10) and (4.6.12) will be integrated for the two

unknowns, ω and ψ. Velocities can be updated by using (4.6.11). We discretize

these equations using the Euler explicit scheme for simplicity. Other integration

formulas, such as the implicit or semi-implicit time stepping schemes, can be

easily substituted for this scheme.

Let us now consider the wall-driven cavity problem outlined in Section 4.5.

We will use the vorticity/stream-function approach to obtain a solution for this

problem. It is possible to use a collocated mesh because the elimination of

the pressure gradient term obviates the use of a staggered mesh to strengthen

pressure–velocity coupling as in the primitive variable system (Section 2.5).

With second-order central differences and Euler-explicit time-advancement, the

ﬁnite-difference form of (4.6.10) is written as

n+1

i, j

−ω

i, j

t

i, j

i+1, j

−ω

i−1, j

i, j

i, j +1

−ω

i, j −1



i+1, j

+ω

i−1, j

+ω

i, j +1

+ω

i, j −1

−4ω

i, j



(4.6.13)

We will assume that the variables have been nondimensionalized by U and L,

the lid velocity and the cavity height, respectively, so that Re = UL/ν;also,

h = x = y. Using the vorticity at the advanced time level (n + 1), the stream

function is calculated from the ﬁnite-difference form of (4.6.12):

n+1

i+1, j

−2ψ

n+1

i, j

+ψ

n+1

i−1, j

n+1

i, j +1

−2ψ

n+1

i, j

+ψ

n+1

i, j −1

=−ω

n+1

i, j

(4.6.14)

Equation (4.6.14) can be solved either by an iterative method or by a direct

method (LU decomposition). The velocity components are updated from (4.6.11):

n+1

i, j

n+1

i, j +1

−ψ

n+1

i, j −1

, v

n+1

i, j

=−

n+1

i+1, j

−ψ

n+1

i−1, j

(4.6.15)

FLOW PAST A CIRCULAR CYLINDER 283

The numerical integration is done according to the following sequence:

1. Set initial conditions at t = 0 (e.g., at all interior points set ω

i, j

= 0).

2. Calculate ω

n+1

i, j

at time level t +t from (4.6.13).

3. Obtain ψ

n+1

i, j

by solving (4.6.14) either by a direct method or iteratively.

4. Update velocities by calculating u

n+1

i, j

and v

n+1

i, j

from (4.6.15).

5. Boundary values for ω

i, j

are solution-dependent and must be updated at

every time step using ψ

n+1

i, j

. We suggest a way of doing that below.

6. If the computation has reached the desired time, or if a prescribed conver-

gence criterion is reached, terminate the calculation; otherwise, go back to

step 2.

7. Monitor the Courant number (which is solution-dependent) and if it starts

to increase rapidly, terminate the calculation and start over with half the

original time step.

For the driven-cavity problem, all boundary conditions are prescribed on

impermeable solid boundaries. Higher-order boundary conditions for vorticity

were developed in Section 3.7, equations (3.7.14) and (3.7.15). Here we provide

an alternative way of writing the boundary conditions for vorticity obtained from

the interior values of the stream function only in the wall-normal direction. Con-

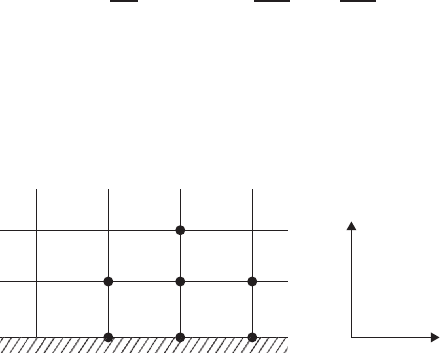
sider Fig. 4.6.1, which shows the vertical grid layout close to the lower stationary

wall, where ψ

n+1

i,1

is the value of the stream function on the wall and ψ

n+1

i,2

the value of the stream function at the ﬁrst point away from the wall; h = y is

the grid length. Using Taylor series up to second order, assuming y is small:

n+1

i,2

= ψ

n+1

i,1



∂ψ

∂y



n+1

i,1

y +



∂

∂y



n+1

i,1

y

+··· (4.6.16)

We now note that when there is no through ﬂow, the boundary condition for the

stream function on solid wall is prescribed as

n+1

i,1

= 0

Δx

Δy

(i, j)

x(i)

y(j)

(i, 2)

(i, 1)

(i − 1, 2)

(i − 1, 1)

(i + 1, 2)

(i + 1, 1)

FIGURE 4.6.1 Grid arrangement close to the stationary lower wall.

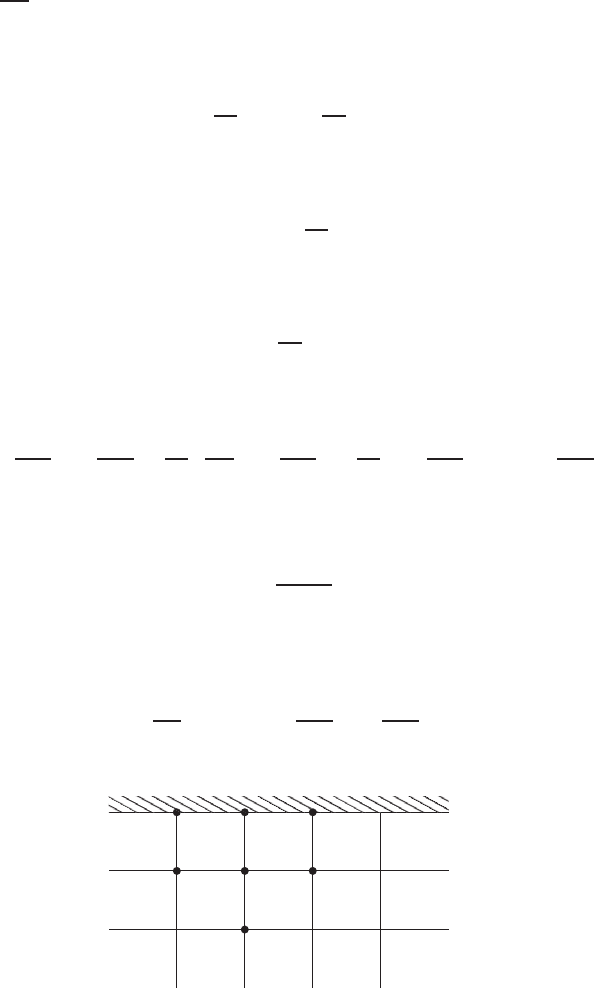
284 NUMERICAL SOLUTION OF THE INCOMPRESSIBLE NAVIER-STOKES EQUATION

Also,



∂ψ

∂y



n+1

i,1

= u

n+1

i,1

= 0 (stationary wall, no slip boundary)

From the deﬁnition of vorticity,

n+1

i,1



∂v

∂x



n+1

i,1

−



∂u

∂y



n+1

i,1

(4.6.17)

Imposing a no-slip boundary condition, we get

n+1

i,1

= 0sothat



∂v

∂x



n+1

i,1

= 0 (4.6.18)

It then follows from (4.6.17) that

n+1

i,1

=−



∂u

∂y



n+1

i,1

(4.6.19)

Hence, (4.6.16) can be written as

n+1

i,2



∂

∂y



n+1

i,1

y

∂

∂y



∂ψ

∂y



n+1

i,1

y



∂u

∂y



n+1

i,1

y

=−ω

n+1

i,1

y

(4.6.20)

which leads to the boundary condition for vorticity on the stationary lower wall

of the cavity:

n+1

i,1

=−

n+1

i,2

y

(4.6.21)

Now, considering the upper wall (Fig. 4.6.2), where the grid index j = J ,and

using Taylor series as before, we have

n+1

i, J −1

= ψ

n+1

i, J

−



∂ψ

∂y



n+1

i, J

y +



∂

∂y



n+1

i, J

y

+··· (4.6.22)

(i − 1, J)

(i − 1, J − 1) (i + 1, J − 1)(i, J − 1)

(i, J)

(i, J − 2)

(i + 1, J)

FIGURE 4.6.2 Grid arrangement close to the moving upper wall.

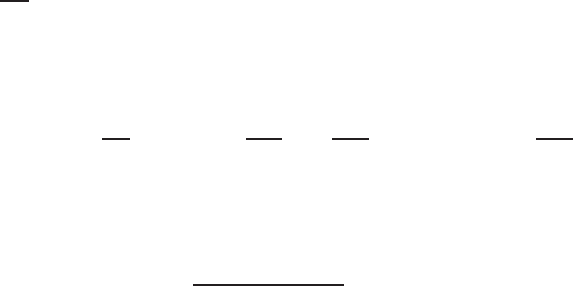
FLOW PAST A CIRCULAR CYLINDER 285

Using the same arguments as before, on solid boundaries with no ﬂow through,

n+1

i, J

= 0, and



∂ψ

∂y



n+1

i, J

= u

n+1

i, J

= u

= 1 (moving wall, no slip boundary) (4.6.23)

Using (4.6.17)–(4.6.19), (4.6.22) can be written as

n+1

i, J −1

=−



∂ψ

∂y



n+1

i, J

y +



∂

∂y



n+1

i, J

y

=−u

y − ω

n+1

i, J

y

(4.6.24)

from which we obtain

n+1

i, J

−ψ

n+1

i, J −1

−u

y

, u

= 1 (4.6.25)

Let us now consider the stream function equation (4.6.14) on a grid with 3 ×3

interior points shown in Fig. 4.6.3:

i+1, j

+ψ

i−1, j

+ψ

i, j +1

+ψ

i, j −1

−4ψ

i, j

=−h

i = 1, 2, ...N

j = 1, 2, ...NN= 3

(4.6.26)

Here, the ﬁrst subscript is the column index along the x direction, and the second

subscript is the row index along the y direction. We can write (4.6.26) for each

internal node:

+ψ

−4ψ

=−h

(1,1)

+ψ

−4ψ

=−h

(2,1)

+ψ

−4ψ

=−h

(3,1)

+ψ

−4ψ

=−h

(1,2)

+ψ

−4ψ

=−h

(2,2)

+ψ

−4ψ

=−h

(3,2)

+ψ

−4ψ

=−h

(1,3)

+ψ

−4ψ

=−h

(2,3)

+ψ

−4ψ

=−h

(3,3)

(4.6.27)

286 NUMERICAL SOLUTION OF THE INCOMPRESSIBLE NAVIER-STOKES EQUATION

4, 43, 42, 41, 40, 44

01234

0, 3 1, 3

2, 3

3, 3 4, 3

4, 23, 22, 21, 20, 2

0, 1 1, 1 2, 1 3, 1 4, 1

0, 0 1, 0 2, 0 3, 0 4, 0

Δy

y(j)

x(i)

FIGURE 4.6.3 Computational grid for the ψ equation (4.6.26).

And in vector-matrix form,

⎡

⎢

⎣

4 −10−100000

−14−10−10000

0 −1400−10 0 0

−1004−10−100

0 −10−14−10−10

00−10−1400−1

000−1004−10

000 0−10−14−1

000 00−10−14

⎤

⎥

⎦

⎡

⎢

⎣

⎤

⎥

⎦

n+1

=−

⎡

⎢

⎣

−h

+ψ

−h

+ψ

−h

+ψ

−h

+ψ

−h

+ψ

−h

+ψ

−h

+ψ

−h

+ψ

⎤

⎥

⎦

n+1

(4.6.28)

The problem again reduces to the solution of the linear equation:

A = f

FLOW PAST A CIRCULAR CYLINDER 287

where A is the banded N

×N

(9 × 9) coefﬁcient matrix; the number of nonzero

bands is 2N +1. We can also write (4.6.28) as follows:

⎡

⎣

BI0

IBI

0IB

⎤

⎦

⎡

⎣

⎤

⎦

⎡

⎣

⎤

⎦

, i = 1, 2, 3

wherewedeﬁneI as the 3 × 3 identity matrix and B is the partitioned diagonal

matrix of A. The direct solution of the linear system A = f can be efﬁciently

done by the LU decomposition method, where we decompose A into a special

upper triangular matrix U and a lower triangular matrix L with the diagonal equal

to unity. The sequential solution of this system is the same as the solution of

the tridiagonal matrix equation given by (4.4.45)–(4.4.46). In a similar fashion,

when the problem requires successive solutions of the elliptic equation, the LU

decomposition can be done only once and storing the L and U matrices, the

back substitution can be performed as many times as needed, thus reducing the

required computational effort. These savings are possible because the cost of the

solution of an n system of linear equations by the LU decomposition method

is n

/2 operations, the same as in Gaussian elimination, but the backsubstitu-

tion part is only n

operations (Ferziger, 1998, p. 5). We also note that for the

ω–ψ formulation of the governing equations, there is no singularity in both the

coefﬁcient matrix of the spatially elliptic ω equation and the coefﬁcient matrix

of the the elliptic ψ equation, so that both can be solved by iterative methods,

such as the successive overrelaxation (SOR) method outlined in Section 2.8,

(2.8.13)–(2.8.14).

Another iterative method that can be efﬁciently employed for the solution

of elliptic equations is the alternating-direction implicit (ADI) method. Let us

consider the elliptic Laplace equation for a generic variable T, in a rectangle

0 < x, y < 1, with Dirichlet boundary conditions on all the sides:

∂

∂x

∂

∂y

= 0 (4.6.29)

The ADI method assumes a pseudo time derivative, so that the equation becomes

elliptic in space and parabolic in time, e.g.,

∂T

∂t

∂

∂x

∂

∂y

(4.6.30)

and seeks steady-state solutions for this problem as t →∞.

Thus, the use of the ADI method for elliptic problems implies that

• Physical signiﬁcance and the accuracy of the transient solution are not of

interest.

• As steady state is approached, that is, when t →∞, the solution approaches

that of the elliptic Laplace (or Poisson) equation.

288 NUMERICAL SOLUTION OF THE INCOMPRESSIBLE NAVIER-STOKES EQUATION

As the transient solution is not important, it is generally sufﬁcient to advance

the solution in time using the fully implicit Euler scheme, so that the two-step

procedure of this method can be written as (Peaceman and Rachford, 1955)

n+1/2

i, j

−T

i, j

t

x



n+1/2

i+1, j

−2T

n+1/2

i, j

+T

n+1/2

i−1, j



y



i, j +1

−2T

i, j

i, j −1



n+1

i, j

−T

n+1/2

i, j

t

x



n+1/2

i+1, j

−2T

n+1/2

i, j

n+1/2

i−1, j



y



n+1

i, j +1

−2T

n+1

i, j

n+1

i, j −1



(4.6.31)

Deﬁning

= x/y, ρ = x

/t

the iteration sequence can be written as

n+1/2

i+1, j

−(2 + ρ)T

n+1/2

i, j

n+1/2

i−1, j

= β



−T

i, j +1



2 −



i, j

−T

i, j −1



n+1

i, j +1

−(2 +

n+1

i, j

n+1

i, j −1



−T

n+1/2

i+1, j

+(2 −ρ)T

n+1/2

i, j

−T

n+1/2

i−1, j



(4.6.32)

Now considering the Poisson equation,

∂T

∂t

=∇

T −ξ(x, y) (4.6.33)

where ξ(x, y) is the source term. For x = y (β

= 1), the ADI sequence can

be written as

n+1/2

i+1, j

−(2 +ρ)T

n+1/2

i−1, j

=−T

i, j +1

+(2 − ρ)T

−T

i, j −1

−x

i, j

n+1

i, j +1

−(2 +ρ)T

n+1

i, j −1

=−T

n+1/2

i+1, j

+(2 −ρ)T

n+1/2

−T

n+1/2

i−1, j

−y

i, j

(4.6.34)

Both set of equations (4.6.32) and (4.6.34) are solved ﬁrst along rows and next

by columns. In both steps, the resulting system of linear equations has tridiagonal

coefﬁcient matrices so that either the Thomas algorithm or the LU decomposi-

tion can be very efﬁciently implemented. It is important to recognize that the

speed of solution convergence depends strongly on the choice of the iteration

parameter, ρ. This method will converge for any ﬁxed value of

ρ for Laplace’s

FLOW PAST A CIRCULAR CYLINDER 289

equation in a square, provided that the same value is used in the two half-steps.

More information concerning different formulations of the ADI method and the

selection of the iteration parameter are given in Mitchell (1969).

Project for Further Study: Program 4.4 is a MATLAB script that numerically

integrates (4.6.10) and (4.6.12) with the Euler explicit scheme on a uniform mesh

with x = y. The solution of the elliptic stream function (ψ) equation (4.6.12)

is obtained by the SOR method. Modify the program and solve (4.6.12) using the

Peaceman-Rachford ADI method outlined above for a grid of 31 ×31 interior

grid points at Reynolds numbers Re = 1, 100, and 400. Note that this equation

has to reach a converged state at every time step during the integration process

and the rate of convergence strongly depends on the proper choice of the iteration

parameter, ρ; for practical purposes, setting ρ ≈ 8/N is sufﬁcient (Ferziger,

1998, p. 265). A parameter sequence for the Peaceman-Rachford method is given

by Wachpress (1957) and summarized by Mitchell (1969, p. 111), which reads

k+1

= (1/ρ

k+1

) =

2cos

(π/2M )



cot



k/(k

−1)

(k = 0, 1, ..., k

−1)

(4.6.35)

In (4.6.35), M is the number of grid divisions so that (M −1) is the number of

interior grid points in one direction. Also, k

is the smallest integer greater than

or equal to 2, obtained from



√

2 − 1



−1)

≤ tan

(4.6.36)

It is important to use the same value of

n each half step of the integration

process. Assuming a 10 ×10 grid of interior points, M = 11, and from

(4.6.36) one obtains k

= 4, which leads to the following sequence of r-values:

0.51033610, 1.85949096, 6.77535187, and 24.68707504. The parameter

sequence can be applied as many times as needed until the imposed convergence

criterion (for example, three orders of magnitude decrease on the amplitude of

the initial error norm) is satisﬁed.

Compare the convergence rates of the solution at different Re, when using

these two convergence criteria.

Flow Past a Circular Cylinder

As a ﬁnal example, we will consider uniform ﬂow, U

∞

, past a circular cylinder

with radius a as shown in Figure 4.6.4. We follow the formulation of this problem

outlined by Peyret and Taylor (1983, pp. 207–212) and, deﬁning the diameter-

based Reynolds number, Re = 2Ua/ν, we write (4.6.12) and (4.6.9), respectively,

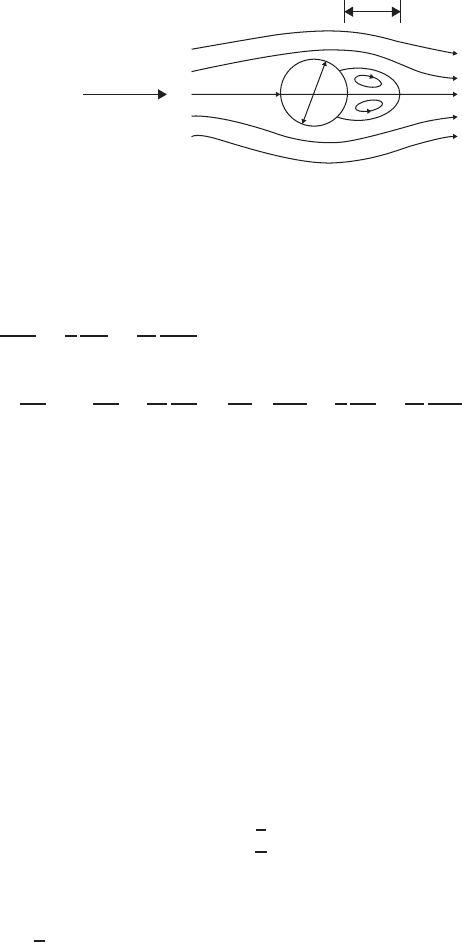
290 NUMERICAL SOLUTION OF THE INCOMPRESSIBLE NAVIER-STOKES EQUATION

∞

FIGURE 4.6.4 Geometry of ﬂow past a circular cylinder, where d is the cylinder diameter,

and L is the separation bubble length.

in cylindrical coordinates:

∂

∂r

∂ψ

∂r

∂

∂θ

=−ω (4.6.37)

∂ω

∂t

∂ω

∂r

∂ω

∂θ



∂

∂r

∂ω

∂r

∂

∂θ



(4.6.38)

where v

and v

are the velocity components along the radial (r) and tangential

(θ) directions, respectively.

The problem consists of the cylinder in quiescent air for time t < 0. At time

t ≥ 0, a uniform velocity U

∞

is applied. The unsteady Navier-Stokes equations

are solved with no-slip boundary conditions on the surface boundary, ,andthe

boundary r →∞has uniform ﬂow. The ﬂow remains symmetrical with respect

to the centerline for low Reynolds numbers, Re < 40. For higher values of Re,

the solution rapidly bifurcates into an oscillatory regime. We will consider low

Re cases exploiting the symmetry of the solution, and investigate the effects of

increasing values of Re on the separation bubble length (L/d) and the drag force

on the cylinder.

It is apparent from the above statements that one major difﬁculty of this

problem is the unbounded physical domain. This difﬁculty can be resolved by

mapping the inﬁnite extent of the physical domain in the r coordinate into a

ﬁnite computational domain by an algebraic transformation given by Ta Phuoc

Loc (1980), such that

r =

= e

πξ

θ = πη

(4.6.39)

In (4.6.39),

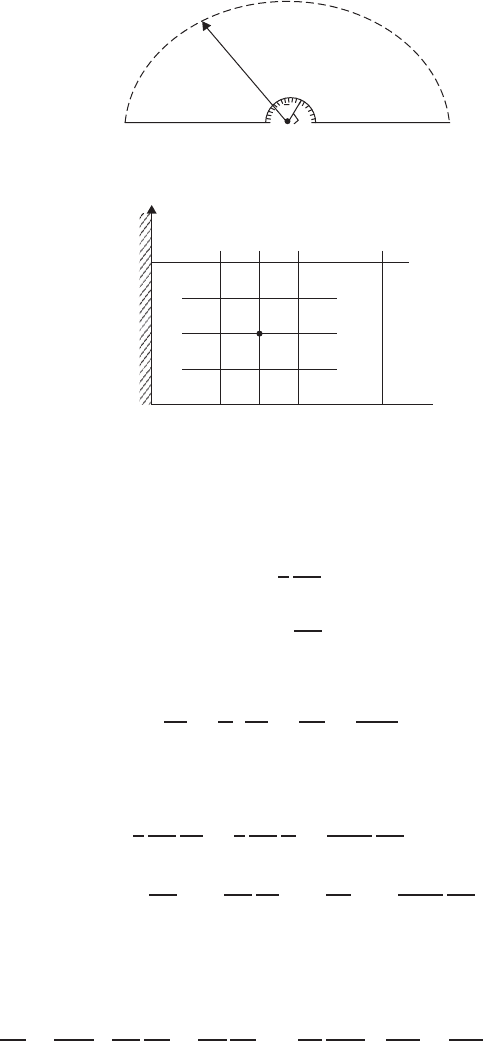
r is the dimensional radius. Because of the symmetry of the solution

at low Re < 40, it is sufﬁcient to calculate the ﬂow ﬁeld in the upper half

of the computational domain, i.e., for 0 ≤ θ ≤ π,sothat0≤ η ≤ 1. Also, the

computational domain is limited to a ﬁnite value ξ

∞

 1, which is equivalent to

∞

= 22, sufﬁciently removed from the surface of the cylinder (Figure 4.6.5).

FLOW PAST A CIRCULAR CYLINDER 291

r, θ

i, j

∞

= 22

η(i)

ζ(j)

∞

FIGURE 4.6.5 Cylinder in uniform ﬂow in transformed coordinates.

In cylindrical coordinates, velocity components are given as

∂ψ

∂θ

=−

∂ψ

∂r

(4.6.40)

Also noting that

∂η

∂θ

∂ξ

∂r

πr

−πξ

(4.6.41)

(4.6.40) can be transformed into the new variables by (4.6.41):

∂ψ

∂η

∂θ

∂ψ

∂η

πe

πξ

∂ψ

∂η

(4.6.42)

=−

∂ψ

∂r

=−

∂ψ

∂ξ

∂r

=−

πr

=−

πe

πξ

∂ψ

∂ξ

(4.6.43)

Substituting (4.6.39)–(4.16.43) into (4.6.37) and (4.6.38), we obtain the govern-

ing equations in the transformed ξ −η coordinates:

∂ω

∂t

g(ξ )



∂ψ

∂η

∂ω

∂ξ

−

∂ψ

∂ξ

∂ω

∂η



g(ξ )



∂

∂ξ

∂

∂η



(4.6.44)