Biringen S., Chow C.-Y. An Introduction to Computational Fluid Mechanics by Example

Подождите немного. Документ загружается.

272 NUMERICAL SOLUTION OF THE INCOMPRESSIBLE NAVIER-STOKES EQUATION

Writing (4.5.59)–(4.5.62) in matrix form, we obtain

A = G

⎡

⎢

⎣

−2110

1 −201

10−21

011−2

⎤

⎥

⎦

⎡

⎢

⎣

⎤

⎥

⎦

⎡

⎢

⎣

⎤

⎥

⎦

(4.5.68)

We can calculate the eigenvalues λ

1−4

of the coefﬁcient matrix, A,usingthe

MATLAB function eig(A), which gives

=−4.0, λ

2,3

=−4.0, λ

= 0.0 (4.5.69)

From (4.5.69), we observe that there is an eigenvalue whose value is zero; there-

fore, the matrix A is singular, cannot be inverted, and (4.5.68) does not have a

solution. We can now use the MATLAB function rcond(A), which calculates the

reciprocal of the condition number of matrix A based on the maximum column

sum of the matrix. If the output rcond(A) is close to zero, the input matrix A is

badly conditioned or singular. If the output is close to 1, then the input matrix is

well conditioned. For the A matrix in (4.5.68), the value of rcond is 1.39e

−17

conﬁrming that the matrix is singular. Mitchell (1969, p. 121) shows that the sin-

gularity of the coefﬁcient matrix of the Neumann problem in elliptic equations is

because the system of equations (4.5.62) is linearly dependent; i.e., the number

of independent equations is one less than the number of unknowns. Thus, one

remedy is to assign a value to one of the unknowns eliminating one variable so

that the number of linearly independent equations will be equal to the number

of remaining unknowns. In this context, let us assign an arbitrary constant value,

= 0. Then the remaining equations can be solved in terms of this constant.

In this case, the matrix equation (4.5.68) becomes



= G

⎡

⎢

⎣

10 0 0

1 −20 1

10−21

01 1−2

⎤

⎥

⎦

⎡

⎢

⎣

⎤

⎥

⎦

⎡

⎢

⎣

⎤

⎥

⎦

(4.5.70)

Here, A

and G

are the modiﬁed coefﬁcient matrix and the modiﬁed right-hand

side vector, respectively. The eigenvalues of A

are

=−0.5858, λ

=−3.4142, λ

=−2.0, (4.5.71)

All the eigenvalues are nonzero; therefore, equations (4.5.65) will have a unique

solution for given values of the right-hand side vector. However, the condition

number of the coefﬁcient matrix A

is 0.1250 so the system is linearly indepen-

dent but still ill-conditioned. Consequently, iterative solutions of this system will

be slower to converge than with Dirichlet-type boundary conditions. Because

PRIMITIVE VARIABLE FORMULATION: NUMERICAL INTEGRATION 273

of the slow convergence, for moderate-size problems, direct solutions based on

LU decomposition will be very efﬁcient. This can be accomplished by using the

MATLAB operation  = A

\ G

Projects for Further Study

1. Numerically integrate the incompressible the continuity equation (4.5.1)

and the Navier-Stokes equation (4.5.2) for a square cavity with a lid moving at a

velocity, U, to the right (Figure 4.5.9). Solve the problem for Reynolds numbers

Re = 100 and Re = 400. For this problem, Re = UL/ν,whereL is the cavity

height and ν is the kinematic viscosity of the ﬂuid. You can incorporate one of

the following methods:

a. Crank-Nicolson (or Euler implicit), Adams-Bashforth (or Euler explicit)

semi-implicit scheme with the fractional step algorithm

b. Fully explicit Euler (or Adams-Bashforth) scheme with the fractional step

algorithm

As the mesh system, use the MAC staggered mesh arrangement. Note that for

the viscous terms the Euler implicit scheme can be written as

∂ζ

∂t

= ν

∂

∂x

n+1

−ζ

t

= ν

n+1

i+1

−2ζ

n+1

+ζ

n+1

i−1

x

+O(t, x

)

(4.5.72)

For the explicit portions of the time step, the diffusive and convective stability

criteria must be obeyed. Generally, the full Neumann boundary conditions of the

pressure equation will require a direct solver (see Section 4.6 for more on direct

solvers). At these values of Re, a 21 ×21 uniform mesh should be sufﬁcient.

Plot the stream function and vorticity contours and compare the values of ψ

FIGURE 4.5.9 Schematic of the driven-cavity problem.

274 NUMERICAL SOLUTION OF THE INCOMPRESSIBLE NAVIER-STOKES EQUATION

and ω at the center of the primary vortex with published data (Ghia, Ghia, and

Shin, 1982; Kim and Moin, 1985). Because the Neumann problem for elliptic

equations is singular (one zero eigenvalue), we must set a reference value for the

pressure; say, on a boundary point set P = 0. This will eliminate one unknown

from the problem (and the related equation also has to be eliminated from the

system as explained in this section, so that the remaining equations will comprise

a linearly independent system of equations. The solution of the system will be

off by a constant, but the pressure gradient will be correctly calculated.

Assume steady state when the error in the solution is reduced by three orders

of magnitude from its initial value. We can use either the maximum magnitude

error norm or the Frobenius error norm for this purpose (Gerald and Wheatley,

1997, p. 156). For example, we deﬁne the error between successive iterates (or

time levels) and the corresponding error norms below:

n+1

i, j

= u

n+1

i+1/2, j

−u

i+1/2, j

F

∞

= max

1≤i≤M



j=1

n+1

i, j

|=maximum magnitude norm (row sum) (4.5.73)

F

⎛

⎝



i=1



j=1



n+1

i, j



⎞

⎠

1/2

= Frobenius norm (Euclidean norm)

These quantities can be readily calculated by MATLAB basic commands norm(F,

inf) and norm(A, ‘fro’), respectively.

Calculate the stream function (ψ) and vorticity (ω) values at the pressure-node

points using the following equations:

ω =

∂v

∂x

−

∂u

∂y

= ψ

i, j −1

+y(u

i, j −1/2

)

(4.5.74)

Note that ψ calculation requires an integration and the ψ equation above is the

discrete form for the staggered mesh. The integration can start from the lower wall

where ψ = 0 and continue along the vertical direction. To calculate u at pressure

nodes, averaging will be required. Assume ψ = 0 on all the solid boundaries.

In Program 4.3 the governing equations are numerically integrated for the

driven-cavity problem with the explicit Euler method; the divergence of the con-

verged velocity ﬁeld was on the order of machine zero (about e-14). We note

that the ﬂow is time dependent as it starts from a quiescent initial state when the

upper lid moves to the right, and it requires many iterations until the ﬂow reaches

steady state. The solution efﬁciency can be signiﬁcantly enhanced if the coefﬁ-

cient matrix of the linear system of the elliptic equations (either resulting from the

implicit time advancement of the viscous terms in the momentum equations, or

as in the present case resulting from the discretization of the “pressure” equation)

PRIMITIVE VARIABLE FORMULATION: NUMERICAL INTEGRATION 275

is declared as sparse; for example,

A = sparse(B)

returns the matrix B in compact form storing all nonzero elements together with

information for the location of each nonzero element in the matrix (row and

column numbers). Operations such as LU decomposition (backslash operation)

will be performed in sparse form if A isasparsematrix.

A more efﬁcient way of accomplishing the same computational efﬁciency with

less storage will be to deﬁne the A matrix (the coefﬁcient matrix of the linear

system),

A = sparse(L, L)

where L is the dimension of A. This statement deﬁnes a zero L ×L matrix

without allocating any storage. When the nonzero components of A are deﬁned,

A is stored and returned in compact form.

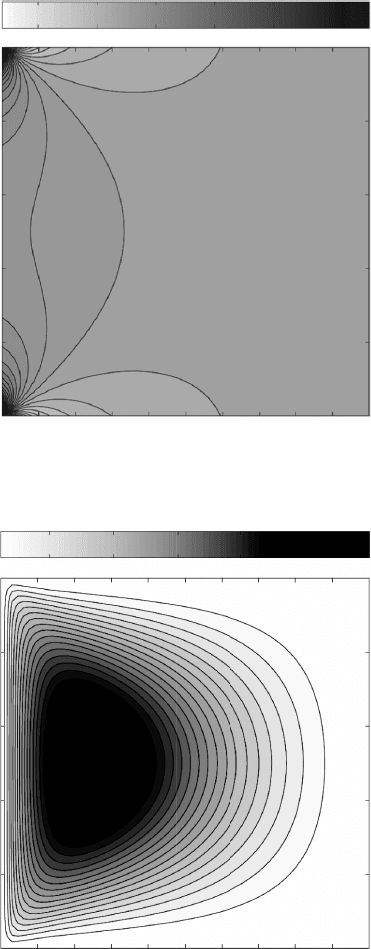
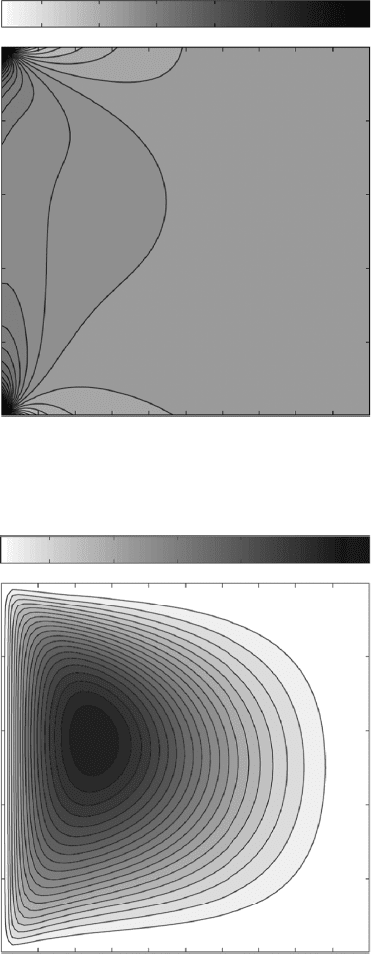
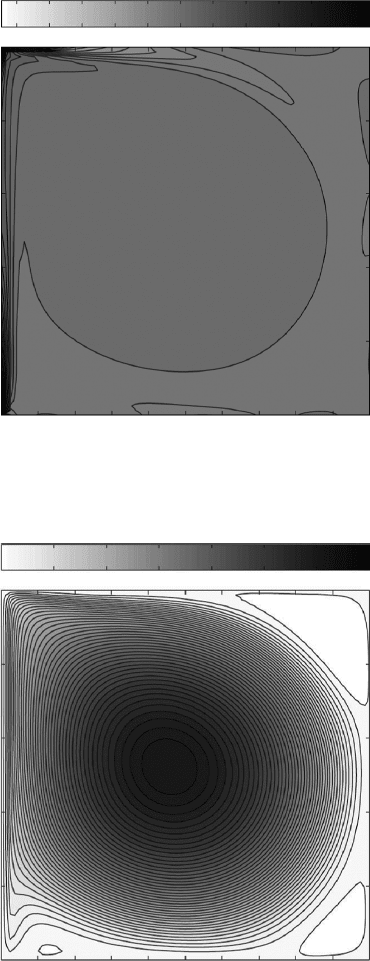
Solutions for the cavity problem for various Reynolds numbers are presented

in Fig. 4.5.10. For Re = 1, the solution has vertical symmetry, as displayed by

the stream function and vorticity contours, and the vorticity is concentrated close

to the upper corners where the problem is singular due to the double value

(0 and 1) of the u velocity at these locations. As the Re increases to Re = 100,

y symmetry is broken and the vortex center moves toward the right upper corner;

a substantial increase to Re = 4000 results in the formation of secondary vortices

in three corners of the cavity. Vorticity is concentrated on the upper and the right

walls, and a vorticity tongue extends deeply into the cavity from the right wall.

Table 4.5.1 summarizes vorticity and stream function values at the center of the

primary vortex for various Reynolds numbers. These values compare favorably

with previous work concerning this ﬂow (see, e.g., Kim and Moin, 1985) for the

comparable number of grid points employed.

2. The shear-driven cavity ﬂow is of interest because of its similarity to wind-

driven ﬂows and can be useful to assess momentum transport from air to water

when the effect of waves on the interface is neglected. Let us assume that at

the air–water interface the shear stress τ = ρ

∗

is constant. The governing

equations (4.5.1) and (4.5.2) are nondimensionalized by the friction velocity u

∗

and the cavity height L,sothatRe= u

∗

L/ν. The physical constants used in

TABLE 4.5.1 Stream Function (ψ

) and Vorticity (ω

)

at the Center of the Primary Vortices; N

and N

Are

the Number of Grid Points along x and y Directions

Re ψ

×N

1 −0.099 −3.207 65 ×65

100 −0.101 −3.157 65 ×65

400 −0.107 −2.609 65 ×65

1000 −0.113 −2.191 81 ×81

4000 −0.113 −1.842 81 ×81

0 0.2 0.4

Stream function contours

Vorticity contours

(a)

x x

0.6 0.8

−0.02

−80

−60

−40

−20

−0.04

−0.06

−0.08

−0.1

−0.12

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.2 0.4 0.6 0.8 1

FIGURE 4.5.10 Streamlines and vorticity contours for the driven cavity. (a) Re = 1, (b) Re = 100, (c) Re = 4000.

276

0 0.2 0.4

Stream function contours

Vorticity contours

0.6 0.8

−0.02

−80

−60

−40

−20

−0.04

−0.06

−0.08

−0.1

−0.12

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.2 0.4 0.6 0.8 1

(b)

x x

FIGURE 4.5.10 (continued)

277

0 0.2 0.4

Stream function contours

Vorticity contours

0.6 0.8

−0.02

−120

−100

−80

−60

−40

−20

−0.06

−0.04

−0.08

−0.1

−0.12

−0.14

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.2 0.4 0.6 0.8 1

(

)

x x

FIGURE 4.5.10 (continued)

278

PRIMITIVE VARIABLE FORMULATION: NUMERICAL INTEGRATION 279

the problem are the kinematic viscosity of water ν = 10

−6

−1

, the density of

water ρ = 1000 kg m

−3

, and the density of air ρ

= 1kg m

−3

. The governing

equations are solved with the following boundary conditions:

At the air water interface (top wall moving from right to left):

∂u

∂y

=−

Re and v = 0

At the solid walls: u = v = 0

Calculate the resulting ﬂow ﬁeld for Re = 100 and for Re = 2000; plot the

stream function and vorticity contours for each value of Re. Also plot u-velocity

proﬁles as a function of the y coordinate at x = 0.5. Finally calculate the values of

ψ = ψ

max

−ψ

min

and compare your results with the published results of Huser

and Biringen (1992). For these steady-state calculations a 41 × 41 uniform mesh

should be adequate.

In summary, the integration of the two-dimensional, unsteady, incompressible

continuity and momentum equations on a rectangular, staggered grid arrange-

ment using the fractional step Euler explicit method can be accomplished by the

following procedure.

Step 1. Prediction step:

• Using (4.5.39) and (4.5.40), calculate ˆu and ˆv at their respective

grid point locations.

• Apply the boundary conditions as described by (4.5.43) or (4.5.44).

Generally, (4.5.43) will be sufﬁcient as the computation sweeps

along the x and y directions.

• These equations will be solved algebraically because time

advancement is fully explicit. Quantities that are not evaluated

at their respective nodes will be evaluated by averaging, as in

(4.5.33)–(4.5.38).

• Linear stability conditions (4.5.41) and (4.5.42) must be obeyed;

in fact, because the equations are nonlinear, especially at higher

Reynolds numbers, these restrictions will have to be multiplied by

a safety factor on the order of 10

−1

and even smaller.

• Divergence of the velocity ﬁeld must be calculated at every time

step, using the velocity ﬁeld at the advanced time level, (n + 1),

∇ · u =

n+1

i+1/2, j

−u

n+1

i−1/2, j

x

−

n+1

i, j +1/2

−u

n+1

i, j −1/2

y

(4.5.75)

The sum of the divergence magnitude at all grid points should be sat-

isﬁed to machine zero at each time step. If this quantity increases,

the calculation should be terminated and restarted with a smaller

time step.

280 NUMERICAL SOLUTION OF THE INCOMPRESSIBLE NAVIER-STOKES EQUATION

Step 2. Pressure calculation:

• Calculate the pressure form the pressure-Poisson equation (4.5.48),

n+1

i, j +1

−2P

n+1

i, j

n+1

i, j −1

y

n+1

i+1, j

−2P

n+1

i, j

n+1

i−1, j

x

t



ˆu

i+1/2, j

− ˆu

i−1/2, j

x

ˆv

i, j +1/2

− ˆv

i, j −1/2

y



(4.5.76)

A direct solver with LU decomposition can be used for the solution

of this equation. This is illustrated in greater in greater detail in

Section 4.6.

• Boundary condition applied to the pressure equation at all bound-

aries is the homogeneous Neumann boundary conditions (4.5.49)

and (4.5.50). This equation is solved at the pressure nodes (i, j)

(Fig. 4.5.3). Note that the Euler explicit time-advancement calcu-

lates the actual thermodynamic pressure (scaled by the constant

density) and not a pseudo-pressure.

• The Neumann problem for the elliptic pressure equation results in a

singular coefﬁcient matrix. To remove this singularity (and obtain a

system of linearly independent equations), it is necessary to assign

a constant value (for example, P = 0) to the pressure at one pres-

sure node. The resulting solution will be off by a constant, but the

pressure gradient will be correctly calculated. A smoother solution

can be obtained by setting the average value of the solution vector

to zero and by imposing this condition in place of one of the nodal

equations.

Step 3. Velocity correction:

• Obtain the velocity ﬁeld at the advanced time level (n + 1) from

(4.5.47); for each velocity component, this equation gives

n+1

i+1/2, j

= ˆu

i+1/2, j

−

t

x



n+1

i+1, j

−P

n+1

i, j



(4.5.77)

n+1

i, j +1/2

= ˆv

i, j +1/2

−

t

x



n+1

i, j +1

−P

n+1

i, j



(4.5.78)

• Steady-state solution at low Reynolds numbers should be assumed

converged when one of the error norms (4.5.73) will decrease by at

least three orders of magnitude.

4.6 FLOW PAST A CIRCULAR CYLINDER: AN EXAMPLE

FOR THE VORTICITY-STREAM FUNCTION FORMULATION

As we have seen in Section 4.3, an alternate formulation of the governing

equations for two-dimensional, steady and unsteady incompressible equations

is the vorticity-stream function formulation where pressure does not appear as

FLOW PAST A CIRCULAR CYLINDER 281

a dependent variable. We can obtain the vorticity transport equation from the

Navier-Stokes equation as follows. First we write the Navier-Stokes equation as

a vector equation:

∂V

∂t

+(V ·∇)V =−∇





+ν∇

V (4.6.1)

where V is the velocity vector, ν is the kinematic viscosity, p is thermodynamic

pressure, and ρ is the ﬂuid density. Using vector identities for the convection

term, we obtain

(V ·∇)V = ∇



V ·V



−V × (∇ × V) (4.6.2)

Substitution of (4.6.2) into (4.6.1) yields

∂V

∂t

+∇



V ·V



−V ×(∇ × V) =−∇





+ν∇

V (4.6.3)

Deﬁning the vorticity vector

ω = ∇ × V (4.6.4)

and noting that the scalar quantity (p/ρ)

∇ × ∇





= 0 (4.6.5)

then from vector identities we can write

V × (∇ ×V) = V × ω (4.6.6)

With (4.6.4)–(4.6.6), after taking the curl equation (4.6.3) becomes

∂ω

∂t

−∇ × (V × ω) = ν∇

ω (4.6.7)

Again, using vector identities, we obtain

∇ × (V ×ω) = V(∇ · ω) − ω(∇ · V) − (V ·∇)ω + (ω · ∇)V

∇ · ω = ∇ · (∇ ×V) = 0 (divergence of the curl of any vector is zero)

∇ · V = 0 (satisﬁes mass conservation for incompressible ﬂow)

(ω ·∇)V = 0 (for two-dimensional ﬂow)

(4.6.8)

The substitution of (4.6.8) into (4.6.7) results in

∂ω

∂t

+(V · ∇)ω = ν∇

ω (4.6.9)