Bhattacharya R., Majumdar M. Random Dynamical Systems: Theory and Applications
Подождите немного. Документ загружается.

2.5 Convergence to Steady States for Markov Processes 133
C
m
= C
m mod(d)
for all m = 0, 1, 2,.... In particular, if the initial state
is in the class C
j
, then the chain cyclically moves back to C
j
in d steps.
Thus if one views p
d
as a one-step transition probability matrix on S,
then the sets C
j
become (disjoint) closed sets ( j = 0, 1,...,d − 1) and
the Markov chain restricted to C
j
is irreducible and aperiodic (i.e., has
period one).
2.5 Convergence to Steady States for Markov Processes
on Finite State Spaces
As will be demonstrated in this section, if the state space is finite, a
complete analysis of the limiting behavior of p
n
,asn →∞, may be car-
ried out by elementary methods that also provide rates of convergence
to the unique invariant distribution. Although, later, the asymptotic be-
havior of general Markov chains is analyzed in detail, including the law
of large numbers and the central limit theorem for Markov chains that
admit unique invariant distributions, the methods of the present section
are also suited for applications to certain more general state spaces (e.g.,
closed and bounded intervals).
First, we consider what happens to the n-step transition law if all states
communicate with each other in one step. In what follows, for a finite set
A, (#A) denotes the number of elements in A.
Theorem 5.1 Suppose S is finite and p
ij
> 0 for all i, j. Then there
exists a unique probability distribution π ={π
j
: j ∈ S} such that
i
π
i
p
ij
= π
j
for all j ∈ S (5.1)
and
)
)
)
p
(n)
ij
− π
j
)
)
)
(1 −(#S)χ)
n
for all i, j ∈ S, n 1, (5.2)
where χ = min{p
ij
: i, j ∈ S} and (#S) is the number of elements in S.
Also, π
j
χ for all j ∈ S and χ 1/(#S).
Proof. Let M
(n)
j
, m
(n)
j
denote the maximum and the minimum, respec-
tively, of the elements {p
(n)
ij
: i ∈ S} of the j th column of p
n
. Since
134 Markov Processes
p
ij
χ and p
ij
= 1 −
k=j
p
ik
1 −[(#S) − 1]χ for all i, one has
M
(1)
j
− m
(1)
j
[1 −((#S) − 1)χ ] −χ = 1 − (#S)χ. (5.3)
Fix two states i , i
arbitrarily. Let J ={j ∈ S: p
ij
> p
i
j
}, J
=
{j ∈ S: p
ij
p
i
j
}. Then,
0 = 1 − 1 =
j
(p
ij
− p
i
j
) =
j∈J
(p
ij
− p
i
j
) +
j∈J
(p
ij
− p
i
j
),
so that
j∈J
(p
ij
− p
i
j
) =−
j∈J
(p
ij
− p
i
j
), (5.4)
j∈J
(p
ij
− p
i
j
) =
j∈J
p
ij
−
j∈J
p
i
j
= 1 −
j∈J
p
ij
−
j∈J
p
i
j
1 −(#J
)χ − (#J)χ
= 1 − (#S)χ. (5.5)
Therefore,
p
(n+1)
ij
− p
(n+1)
i
j
=
k
p
ik
p
(n)
kj
−
k
p
i
k
p
(n)
kj
=
k
(p
ik
− p
i
k
)p
(n)
kj
=
k∈J
(p
ik
− p
i
k
)p
(n)
kj
+
k∈J
(p
ik
− p
i
k
)p
(n)
kj
k∈J
(p
ik
− p
i
k
)M
(n)
j
+
k∈J
(p
ik
− p
i
k
)m
(n)
j
=
k∈J
(p
ik
− p
i
k
)M
(n)
j
−
k∈J
(p
ik
− p
i
k
)m
(n)
j
=
M
(n)
j
− m
(n)
j
k∈J
(p
ik
− p
i
k
)
(1 − (#S)χ)
M
(n)
j
− m
(n)
j
. (5.6)
Letting i , i
be such that p
(n+1)
ij
= M
(n+1)
j
, p
(n+1)
i
j
= m
(n+1)
j
, one gets from
(5.6),
M
(n+1)
j
− m
(n+1)
j
(1 −(#S)χ)
M
(n)
j
− m
(n)
j
. (5.7)

2.5 Convergence to Steady States for Markov Processes 135
Iteration now yields, using (5.3) as well as (5.7),
M
(n)
j
− m
(n)
j
(1 −(#S)χ)
n
for n 1. (5.8)
Now
M
(n+1)
j
= max
i
p
(n+1)
ij
= max
i
k
p
ik
p
(n)
kj
max
i
k
p
ik
M
(n)
j
= M
(n)
j
,
m
(n+1)
j
= min
i
p
(n+1)
ij
= min
i
k
p
ik
p
(n)
kj
min
i
k
p
ik
m
(n)
j
= m
(n)
j
,
i.e., M
(n)
j
is nonincreasing and m
(n)
j
is nondecreasing in n. Since M
(n)
j
, m
(n)
j
are bounded above by 1, (5.7) now implies that both sequences have the
same limit, say π
j
. Also χ
m
(1)
j
m
(n)
j
π
j
M
(n)
j
for all n, so that
π
j
χ for all j and
m
(n)
j
− M
(n)
j
p
(n)
ij
− π
j
M
(n)
j
− m
(n)
j
,
which, together with (5.8), implies the desired inequality (5.2).
Finally, taking limits on both sides of the identity
p
(n+1)
ij
=
k
p
(n)
ik
p
kj
(5.9)
one gets π
j
=
k
π
k
p
kj
, proving (5.1). Since
j
p
(n)
ij
= 1, taking lim-
its, as n →∞, it follows that
j
π
j
= 1. To prove uniqueness of the
probability distribution π satisfying (5.1), let ¯π ={¯π
j
: j ∈ S}be a prob-
ability distribution satisfying ¯π
p = ¯π
. Then by iteration it follows that
¯π
j
=
i
¯π
i
p
ij
= ( ¯π
pp)
j
= ( ¯π
p
2
)
j
=···=( ¯π
p
n
)
j
=
i
¯π
i
p
(n)
ij
.
(5.10)
Taking limits as n →∞, one gets ¯π
j
=
i
¯π
i
π
j
= π
j
.
Thus, ¯π = π.
136 Markov Processes
It is also known (see Complements and Details) that for an irreducible,
aperiodic Markov chain on a finite state space S there is a positive integer
v such that
χ
:= min
i, j
p
(v)
ij
> 0. (5.11)
Applying Theorem 5.1 with p replaced by p
v
one gets a probability
π ={π
j
: j ∈ S} such that
max
i, j
)
)
)
p
(nv)
ij
− π
j
)
)
)
(1 − (#S)χ
)
n
, n = 1, 2,..... (5.12)
Now use the relations
)
)
)
p
(nv+m)
ij
− π
j
)
)
)
=
)
)
)
)
)
k
p
(m)
ik
(p
(nv)
kj
− π
j
)
)
)
)
)
)
k
p
(m)
ik
(1 − (#S)χ
)
n
= (1 − (#S)χ
)
n
m 1 (5.13)
to obtain
)
)
)
p
(n)
ij
− π
j
)
)
)
(1 −(#S)χ
)
[n/v]
, n = 1, 2,..., (5.14)
where [x] is the integer part of x. From here one obtains the following
corollary to Theorem 5.1:
Corollary 5.1 Let p be an irreducible and aperiodic transition matrix
on a finite state space S. Then there is a unique probability distribution
π on S such that,
π
p = π
. (5.15)
Also,
)
)
)
p
(n)
ij
− π
j
)
)
)
(1 −#Sχ
)
[n/v]
for all i, j ∈ S, n ≥ 1, (5.16)
where χ
> 0 and v are as in (5.11).
Notation To indicate the initial distribution, say, µ, we will often write
P
µ
for P, when X
0
has a distribution µ. In the case when µ = δ
i
, a point
mass at i, i.e., µ({i}) = 1, we will write P
i
instead of P
δ
i
. Expectations
under P
µ
and P
i
will be often denoted by E
µ
and E
i
, respectively.
2.5 Convergence to Steady States for Markov Processes 137
Example 5.1 (Bias in the estimation of Markov models under hetero-
geneity) Consider the problem of estimating the transition probabilities
of a two-state Markov model, e.g., with states “employed” (labeled 0)
and “unemployed” (labeled 1). If the population is homogeneous, with
all individuals having the same transition probabilities of moving from
one state to the other in one period, and the states of different individu-
als evolve independently (or, now in a manner such that the law of large
numbers holds for sample observations), then the proportion in a random
sample of those individuals moving to state 1 from state 0 in one period
among those in state 0 is an unbiased estimate of the corresponding
true transition probability, and as the sample size increases the estimate
converges to the true value (consistency).
Suppose now that the population comprises two distinct groups of
people, group I and group II, in proportions θ and 1 − θ, respectively
(0 <θ <1). Assume that the transition probability matrices for the two
groups are
1−p−ε p + ε
q −ε 1−q + ε
,
1−p + ε p−ε
q + ε 1−q −ε
,
0< p−ε<p + ε<1,
0 −q −ε<q + ε<1.
.
The steady state distributions of the two groups are
q − ε
p + q
,
p + ε
p + q
and
q + ε
p + q
,
p − ε
p + q
.
Assume that both groups are in their respective steady states. Then the
expected proportion of individuals in the overall population who are in
state 0 (employed) at any point of time is
θ
q − ε
p + q
+ (1 −θ)
q + ε
p + q
=
q + ε(1 − 2θ )
p + q
. (5.17)
Now, the expected proportion of those individuals in the population who
are in state 0 at a given time and who move to state 1 in the next period
of time is
θ
q − ε
p + q
(p + ε) + (1 −θ )
q + ε
p + q
(p − ε)
=
pq − (1 − 2θ)(q − p)ε − ε
2
p + q
. (5.18)

138 Markov Processes
Dividing (5.18) by (5.17), we get the overall (transition) probability of
moving from state 0 to state 1 in one period as
pq − (1 − 2θ)(q − ε)ε
q + ε(1 − 2θ )
= p +
2θqε − qε − ε
2
q + ε(1 − 2θ )
. (5.19)
Similarly, the overall (transition) probability of moving from state 1 to
state 0 in one period is given by
q +
−2θpε + pε − ε
2
p − ε(1 − 2θ)
. (5.20)
If one takes a simple random sample from this population and computes
the sample proportion of those who move from state 0 to state 1 in one
period, among those who are in state 0 initially, then it would be an
unbiased and consistent estimate of
θ(p + ε) + (1 − θ)(p − ε) = p + 2θε − ε = p − ε(1 − 2θ). (5.21)
This follows from the facts that (1) the proportion of those in the sam-
ple who belong to group I (respectively, group II) is an unbiased and
consistent estimate of θ (respectively, 1 − θ) and (2) the proportion of
those moving to state 1 from state 0 in one period, among individuals in
a sample from group I (respectively, group II), is an unbiased and con-
sistent estimate of the corresponding group probability, namely, p + ε
(respectively, p − ε).
It is straightforward to check (Exercise) that (5.21) is strictly larger
than the transition probability (5.19) in the overall population, unless
θ = 0 or 1 (i.e., unless the population is homogeneous). In other words,
the usual sample estimates would overestimate the actual transition prob-
ability (5.19) in the population. Consequently, the sample estimate would
underestimate the population transition probability of remaining in state
0 in the next period, among those who are in state 0 initially at a given
time.
Similarly, the sample proportion in a simple random sample of those
who move to state 0 from state 1 in one period, among those who are in
state 1 initially in the sample, is an unbiased and consistent estimate of
θ(q − ε) + (1 −θ )(q + ε) = q + ε(1 − 2θ ), (5.22)
but it is strictly larger than the population transition probability (5.20)
it aims to estimate (unless θ = 0 or 1). Consequently, the population

2.5 Convergence to Steady States for Markov Processes 139
transition probability of remaining in state 1 in the next period, starting in
state 1, is underestimated by the usual sample estimate, if the population
is heterogeneous.
Thus, in a heterogeneous population, one may expect (1) a longer pe-
riod of staying in the same state (employed or unemployed) and (2) a
shorter period of moving from one state to another, than the correspond-
ing estimates based on a simple random sample may indicate.
This example is due to Akerlof and Main (1981).
Let us now turn to periodicity. Consider an irreducible, periodic
Markov chain on a finite state space with period d > 1. Then p
d
viewed
as a one-step transition probability on S has d (disjoint) closed sets C
j
( j = 0,...,d − 1), and the chain restricted to C
j
is irreducible and ape-
riodic. Applying Corollary 5.1 there exists a probability π
( j)
on C
j
, which
is the unique invariant distribution on C
j
(with respect to the (one-step)
transition probability p
d
), and there exists λ
j
> 0 such that
)
)
)
p
(nd)
ik
− π
( j)
k
)
)
)
≤ e
−nλ
j
for all i, k ∈ C
j
, n ≥ 1,
(π
( j)
)
p
d
= (π
( j)
)
;(j = 0, 1,...,d − 1). (5.23)
More generally, identifying j +r with j + r (mod d),
p
(nd+r)
ik
=
k
∈C
j+r
p
(r)
ik
p
(nd)
k
k
=
k
∈C
j+r
p
(r)
ik
π
( j+r)
k
+ O(e
−nλ
k
)
= π
( j+r)
k
+ O(e
−nλ
k
)(i ∈ C
j
, k ∈ C
j+r
)
p
(nd+r)
ik
= 0ifi ∈ C
j
and k /∈ C
j+r
. (5.24)
Now extend π
( j)
to a probability on S by setting π
( j)
i
= 0 for all i /∈ C
j
.
Then define a probability (vector) π on S by
π =
1
d
d−1
j=0
π
( j)
. (5.25)
Theorem 5.2 Consider an irreducible periodic Markov chain on a finite
state space S, with period d > 1. Then π defined by (5.25) is the unique
invariant probability on S, i.e., π
p = π
, and one has
p
(nd+r)
ik
=
dπ
k
+ O(e
−λn
) if i ∈ C
j
,k∈ C
j+r
,
0 i ∈ C
j
, k /∈ C
j+r
,
(5.26)
140 Markov Processes
where λ = min{λ
j
: j = 0, 1,...,d − 1}. Also, one has
lim
N →∞
1
N
N
m=1
p
(m)
ik
= π
k
(i, k ∈ S). (5.27)
Proof. Relations (5.26) follow from (5.23), and the definition of π in
(5.25). Summing (5.26) over r = 0, 1,...,d − 1, one obtains
d−1
r=0
p
(nd+r)
ik
= dπ
k
+ O(e
−λn
)(i, k ∈ S), (5.28)
so that
1
nd
nd
m=1
p
(m)
ik
=
1
nd
d−1
r=1
p
(r)
ik
+ p
(nd)
ik
+
n−1
m=1
d−1
r=0
p
(md+r)
ik
= O
1
n
+
1
nd
n−1
m=1
dπ
k
+ O(e
−λm
)
= π
k
+ O
1
n
(i, k ∈ S). (5.29)
Since every positive integer N can be expressed uniquely as N = nd +r ,
where n is a nonnegative integer and r = 0, 1,..., or d − 1, it follows
from (5.29) that
1
N
N
m=1
p
(m)
ik
=
1
nd + r
nd
m=1
p
(m)
ik
+
1≤r
≤r
p
(nd+r
)
ik
=
nd
nd + r
π
k
+ O
1
n
= π
k
+ O
1
N
,
yielding (5.27).
To prove the invariance of π, multiply both sides of (5.27) by p
kj
and
sum over k ∈ S to get
lim
N →∞
1
N
N
m=1
p
(m+1)
ij
=
k∈S
π
k
p
kj
. (5.30)
2.5 Convergence to Steady States for Markov Processes 141
But, again by (5.27), the left-hand side also equals π
j
. Hence
π
j
=
k∈S
π
k
p
kj
( j ∈ S), (5.31)
proving invariance of π: π
= π
p. To prove uniqueness of the invariant
distribution, assume µ is an invariant distribution. Multiply the left-hand
side of (5.27) by µ
i
and sum over i to get µ
k
. The corresponding sum on
the right-hand side is π
k
, i.e., µ
k
= π
k
(k ∈ S).
From the proof of Theorem 5.2, the following useful general result
may be derived (Exercise):
Theorem 5.3 (a) Suppose there exists a state i of a Markov chain and a
probability π = (π
j
:j∈ S) such that
lim
n→∞
1
n
n
m=1
p
(m)
ij
= π
j
for all j ∈ S. (5.32)
Then π is an invariant distribution of the Markov chain.
(b) If π is a probability such that (5.32) holds for all i, then π is the
unique invariant distribution.
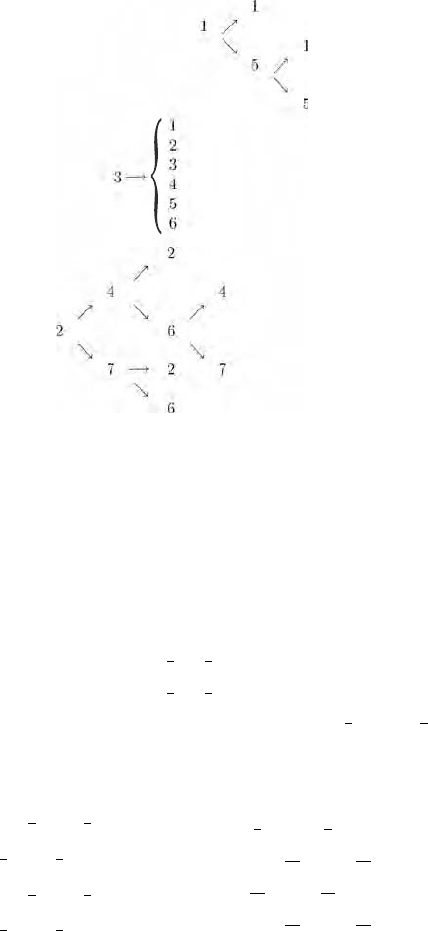
Example 5.2 Consider a Markov chain on S ={1, 2,...,7} having the
transition probability matrix
p =
1
3
000
2
3
00
000
1
3
00
2
3
1
6
1
6
1
6
1
6
1
6
1
6
0
0
1
2
000
1
2
0
2
5
000
3
5
00
000
5
6
00
1
6
0
1
4
000
3
4
0
142 Markov Processes
1 3.
The schematic diagram above shows that 3 is the only inessential state,
so that E ={1, 2, 4, 5, 6, 7}. There are two closed sets of communicating
states, E
1
={1, 5} and E
2
={2, 4, 6, 7} of which E
1
is aperiodic and E
2
is periodic of period 2. When the chain is restricted to E
1
, the Markov
chain on E
1
has the transition probability matrix
15
p
(1)
=
1
5
1
3
2
3
2
5
3
5
,
which has the unique invariant probability ˜π = (˜π
1
=
3
8
, ˜π
5
=
5
8
)
.For
the Markov chain on E
2
one has the transition probability matrix p
(2)
given by
24 67 2 4 6 7
p
(2)
=
2
4
6
7
0
1
3
0
2
3
1
2
0
1
2
0
0
5
6
0
1
6
1
4
0
3
4
0
(p
(2)
)
2
=
2
4
6
7
1
3
0
2
3
0
0
7
12
0
5
12
11
24
0
13
24
0
0
17
24
0
7
24
.
The two cyclic classes are C
0
={2, 6} and C
1
={4, 7},
