Безруков А.Б., Саитгараев С.С. Прикладная теория игр
Подождите немного. Документ загружается.

31
Множество ситуаций в смешанных стратегиях для матричной
игры определяется как декартово произведение:
{X}= {X
1
}×{X
2
} . (2.16)
Смешанным расширением матричной игры является тройка:
Г=({X
1
},{X
2
},H(X)) . (2.17)
Это смешанное расширение также является антагонистической
игрой, причем в этой игре множества чистых стратегий каждого игро-
ка с учетом условий (2.12), (2.13) будут бесконечными. Таким образом,
при переходе к смешанным стратегиям происходит как бы бесконеч-
ное “дробление” матрицы исходной игры в чистых стратегиях.
Даже интуитивно очевидно, что такая “сильно дробная” матри-
ца будет доставлять игре, по крайней мере, одну седлов ую точку.
Строгое доказательство этого факта опирается на теорему о непод-
вижной точке либо на теорему об отделимости выпуклого множества
от точки в евклидовом пространстве. Оно достаточно громоздко и
здесь опускается.
Применение смешанных стратегий превращает игр у в некоторое
случайное испытание, исходом которого является ситуация X=(X
1
, X
2
).
Отсутствие какого-либо обмена информацией между игроками
(т.к. антагонистическая игра в принципе бескоалиционна) делает их
случайные выборы своих чистых стратегий независимыми. Поэтому
если игроки применяют смешанные стратегии X
1
и X
2
, то каждая си-
туация в чистых стратегиях (х
1
и х
2
)
реализуются с вероятностью
X
1
(x
1
)·X
2
(x
2
). Отсюда математическое ожидание выигрыша 1-го игро-
ка можно вычислить:
)x(X)x(X)x,x(H)X,X(H)X(H
221121
}x{x}x{x
21
2211
⋅⋅==
∑∑
∈
∈
(2.18)
или в матричной векторной форме:
T
2
1jiij
n
1j
m
1i
21
XHXh)X,X(H)X(H
=η⋅ξ⋅==
∑∑
==
. (2.19)
Выражения (2.18), (2.19) приводят к понятию смешанного рас-
ширения матричной игры.
Как упоминалось выше, в смешанном расширении любая мат-
ричная игра имеет хотя бы одну ситуацию равновесия. Ситуация
)X,X(
21
∗∗
считается равновесной (устойчивой по Нэшу) если для лю-
бых X
1
, X
2
выполняется неравенство
)X,X(H)X,X(H)X,X(H
212121
∗∗∗∗
≤≤
. (2.20)
Стратегия каждого игрока называется оптимальной, если суще-
ствует стратегия другого игрока, в паре с которой она образуе т ситуа-
цию равновесия. Каждый игрок имеет хотя бы одну оптимальную
32
стратегию. Множество всех ситуаций равновесия есть декартово про-
изведение множеств оптимальных стратегий 1-го и 2-го игроков, соот-
ветственно, выигрыши во всех ситуациях равновесия одинаковы и
равны цене игры. Таким образом, всякую тройку
ν
∗
∗
,X,X
(
21
) можно
считать решением матричной игры.
Спектром смешанной стратегии игрока в конечной антагони-
стической игре называется множество тех его чистых стратегий, для
которых
0≠
ξ
(если это 1-й игрок) и
0≠η
(если 2-й игрок). Чистые
стратегии, входящие в спе ктр оптимальных стратегий, называются
активными стратегиями. Можно сформулировать теорему о допол-
няющей нежесткости, аналогичную теореме в линейном программиро-
вании: ес ли X
2
произвольная оптимальная смешанная стратегия игрока
2 в матричной игре Г и для чистой стратегии
0
i
1
x
игрока 1 имеет место
неравенство
∑
=
ξν<η
n
1j
ijji
00
то,h
=0. (2.21)
В иной, контрапозитарной форме эту теорему можно сформули-
ровать таким образом: если стратегия
0
i
1
x
игрока 1 входит в спектр
некоторой его оптимальной смешанной стратегии, то для любой опти-
мальной стратегии второго игрока
∑
=
ν=η
n
1j
jji
0
h
. (2.22)
Двойственную теорему можно сформулировать для чистой
стратегии
0
j
2
x
игрока 2.
2.5. Аналитический метод решения игр 2×
××
×2
Пусть игра 2×2 задана платежной матрицей
=
2221
1211
hh
hh
H
Пусть седловой точки нет и, следовательно, нижняя цена игры
не равна верхней: α≠β. Требуется найти оптимальную смешанную
стратегию игрока A .
ξξ
=
x
2
x
1
2
1
1
1
*
1
xx
X
Она отличается тем свойством, что, каковы бы ни были дейст-
вия противника (если только он не выходит за пределы своих
“полезных” (ак тивных) стратегий), выигрыш будет равен цене игры ν.
В игре 2×2 обе стратегии противника являются “полезными”, – иначе
игра имела бы решение в области чис тых стратегий (седловую точку).

33
Значит, если мы придерживаемся своей оптимальной стратегии
*
1
X
, то
противник может пользоваться любой из своих чистых стратегий
2
2
1
2
x,x
, не изменяя среднего выигрыша ν.
То есть, если игрок В использует чистую стратегию
1
2
x
(это со -
ответствует 1-му столбцу платежной матрицы), выигрыш игрока A,
применяющего смешанную стратегию, равен цене игры ν:
ν=ξ⋅+ξ⋅
*
221
*
111
hh
.
Тот же средний выигрыш получает игрок A, если 2-й игрок
применяет стратегию
2
2
x
, т.е.
ν=ξ⋅+ξ⋅
*
222
*
112
hh
. Учитывая, что
1
*
2
*
1
=ξ+ξ
, получаем систему уравнений для определения оптималь-
ной стратегии
*
1
X
и цены игры ν:
ν=ξ⋅+ξ⋅
*
221
*
111
hh
,
ν=ξ⋅+ξ⋅
*
222
*
112
hh
, (2.23)
1
*
2
*
1
=ξ+ξ
.
Решая эту систем у, получим оптимальную стратегию
21122211
2122
*
1
hhhh
hh
−−+
−
=ξ
, (2.24)
21122211
1211
*
2
hhhh
hh
−−+
−
=ξ
и цену игры
21122211
21121122
hhhh
hhhh
−−+
⋅−⋅
=ν
(2.25)
Применяя теорему об активных стратегиях при отыскании
*
2
X
–
оптимальной стратегии игрока B, получаем, что при любой чистой
стратегии игрока A (
2
1
1
1
xилиx
) средний проигрыш игрока B равен
цене игры ν, т.е.
ν=η⋅+η⋅
*
212
*
111
hh
,
ν=η⋅+η⋅
*
222
*
121
hh
, (2.26)
1
*
2
*
1
=η+η
.
Тогда оптимальная стратегия
),(X
*
2
*
12
ηη
определяется форму-
лами:
21122211
1222
*
1
hhhh
hh
−−+
−
=η
, (2.27)
21122211
2111
*
2
hhhh
hh
−−+
−
=η
.
34
2.6. Графоаналитический метод решения игр 2×
××
×n и m×
××
×2
Решение игры 2×2 допускает наглядную геометрическую ин-
терпретацию. Пусть игра задана матрицей H= (h
ij
), i, j=1,2, приведен-
ной ниже
В
А
1
2
x
2
2
x
1
1
x
h
11
h
12
2
1
x
h
21
h
22
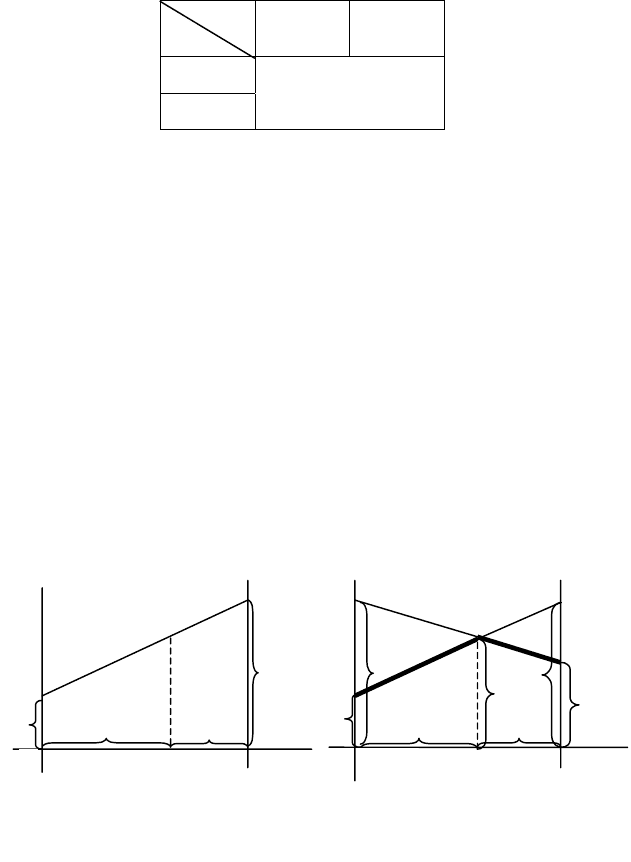
Возьмем участок оси абсцисс длиной 1 (как сумма вероятностей
ξ
1
+ ξ
2
=1) – рис. 2.2. Левый конец участка (точка с абсциссой х=0) бу-
дет изображать стратегию
1
1
x
, правый конец участка (х=1) – стратегию
2
1
x
. Проведем через точки
1
1
x
и
2
1
x
два перпендикуляра к оси абсцисс:
ось I-I и ось II-II. На оси I-I будем откладывать выигрыши при страте-
гии
1
1
x
, на оси II-II – выигрыши при стратегии
2
1
x
. Рассмотрим страте-
гию противника
1
2
x
; она дает две точки на осях I-I и II-II c ординатами,
соответственно, h
11
и h
21
. Проведем через эти точки прямую
1
2
1
2
xx
−
.
Очевидно, есл и мы будем применять смешанную стратегию
ξξ
=
21
2
1
1
1
1
xx
X
а игрок В – чистую стратегию
1
2
x
, то наш средний выигрыш, равный
h
11
·ξ
1
+ h
21
· ξ
2
, изобразится точкой М на прямой
1
2
1
2
xx
−
; абсцисса этой
точки равна ξ
2
. Прямую
1
2
1
2
xx
−
, изображающую выигрыш при страте-
гии
1
2
x
, условно будем называть “стратегией
1
2
x
”.
Очевидно, точно таким же способом может быть построена и
стратегия
2
2
x
(рис. 2.3).
0
1
1
x
h
11
ν
h
12
h
11
h
22
2
2
x
2
1
x
1
1
x
2
1
x
2
2
x
1
2
x
1
2
x
1
1
2
x
1
2
x
0
1
M
N
ξ
2
ξ
1
ξ
1
ξ
2
h
21
X
X
I
I
II II
I
I
II
II
h
21
Рис. 2.2
Рис. 2.3
35
Нам нужно найти оптимальную стратегию
*
1
X
, то есть такую,
для которой минималь ный выигрыш (при любом поведении В) обра-
щался бы в максимум. Для этого построим нижнюю границу выигры-
ша при стратегиях
2
2
1
2
x,x
, то есть ломаную
2
2
1
2
xNx
−−
, отмечен-
ную на рис. 2.3 жирной линией. Эта нижняя граница будет выражать
минимальный выигрыш игрока А при любых смешанных его стратеги-
ях; точка N, в которой этот минимальный выигрыш достигает макси-
мума, и определяет решение и цену игры. Нетрудно убедиться, что
ордината точки N есть цена игры ν, а ее абсцисса равна
*
2
ξ
– частоте
применения стратегии
2
1
x
в оптимальной смешанной стратегии
*
1
X
.
Геометрическая интерпретация дает возможность представить
наглядно также нижнюю и верхнюю цену игры.
Пусть в игре Г 1-й игрок имеет чистые стратегии
2
1
1
1
xиx
, а 2-й
игрок – n чистых стратегий
n
2
2
2
1
2
x,...,x,x
. Тогда фундаментальный
симплекс смешанных стратегий 1-го игрока есть отрезок [0;1]. Коор-
дината ξ на этом отрезке есть вероятность применения
1
1
x
. Теперь до-
пустим, что 2-й игрок выбрал j-ю чистую стратегию
j
2
x
. В этом случае
выигрыш 1-го игрока (или проигрыш 2-го) будет зависеть от ситуации
j
2
i
1
x,x(
), то есть от вероятности
)x(X
i
1
=ξ
, так как 2-й игрок уже вы-
брал стратегию
j2j1j)(11
j
2
h)1(h]H[XH:x ⋅ξ−+⋅ξ==
⋅
.
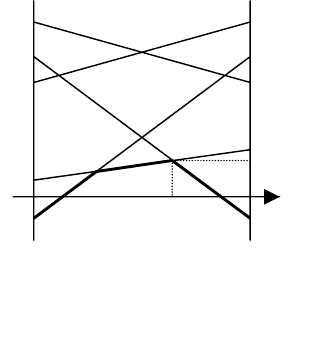
Этот выигрыш линейно зависит от ξ и изображается на графике
прямой линией. Каждой j-й стратегии 2-го игрока будет соответство-
вать своя прямая (рис. 2.4).
Графиком функции от пере-
менной ξ
==
⋅ j)(11
HXminHmin
[
]
j2j1
h)1(hmin
ξ
−+⋅
ξ
=
будет
нижняя огибающая семейства
прямых, которая на рис. 2.4 вы-
делена жирной обводкой. Эта
функция вогнута (выпукла
вверх) и ее максимум есть
j
)
(
1
j
X
H
X
minmax
1
⋅
, (точка М на
рис. 2.4). Абсцисса точки М есть
оптима льная в смысле равновес-
ности стратегия 1-го игрока ξ
*
, а
ордината – цена игры в смешан-
ных стратегиях ν.
0
H
ξ
ν
M
ξ*
H
Рис.2.4
M – точка “пика”

36
Точка пика может иметь абсциссу, равную 0 или 1, а также рав-
ную произвольному числу из интервала (0;1). В первом случае опти-
мальная стратегия 1-го игрока есть чистая ξ
*
=0 , во втором – ξ
*
=1, а
оптимальные стратегии 2-го игрока – это те его чистые стратегии, ко-
торым соответствуют прямые, подходящие к пиковой точке ( с отрица-
тельным наклоном, если ξ
*
=0 и с положительным, если ξ*=1). Все ли-
нейные комбинации этих чистых стратегий также будут оптимальны-
ми для 2-го игрока.
Если абсц исса пика 0<ξ
*
<1, то графически это выглядит как пе-
ресечение в одной точке не менее 2 прямых, хотя бы две из которых
имеют разные по знаку наклоны (рис. 2.4). Уравнения этих двух пря-
мых имеют вид:
1
j2
1
j1
1
j2
hh(hH −
ξ
+=
) , (2.28)
2
j2
2
j1
2
j2
hh(hH −
ξ
+=
) , (2.29)
то есть 1-я прямая соответствует выбору вторым игроком стратегии j
1
,
а 2-я – выбору стратегии j
2
.
Если 2-й игрок откажется от всех прочих стратегий кроме j
1
и j
2
,
то в новой игре формата 2×2 цена игры и оптимальная стратегия 1-го
игрока ξ
*
останутся прежними. Это означает, что оперируя только
стратегиями j
1
и j
2
, 2-й игрок может позволить 1-му игроку получить
лишь гарантированный результат ν. Таким образом, оптимальная стра-
тегия 2-го игрока может быть получена как линейная форма стратегий
j
1
и j
2
с вероятностными весами η
*
и 1-η
*
. Для вычисления η
*
исполь-
зуется формула :
2121
1
2
j1j2j1j1
j1j2
*
hhhh
hh
−−−
−
=η
. (2.30)
Пусть теперь в матричной игре Г 1-й игрок имеет m чистых
стратегий, а 2-й игрок – только 2 чистых стратегии. Графоаналитиче-
ское решение такой игры сходно с решением игры формата 2×n. Сме-
шанная стратегия 2-го игрока в этом случае имеет вид X
2
=(η; 1-η), и
их множество принадлежит отрезку [0;1].
Если 1-й игрок выбрал i-ю чистую стратегию, а 2-й игрок –сме-
шанную стратегию X
2
, то выигрыш 1-го игрока (т.е. проигрыш
2-го) будет равен:
).1(hhXHH
2
1
ii
T
2
)(i
η−+η=⋅=
⋅
(2.31)
Зависимость этого выигрыша от переменных η линейна,
а график есть прямая линия. Графиком функции
[
]
)
1
(
h
h
max
X
H
2
1
ii
i
2
)(i
η
−
+
η
=⋅
⋅
буде т являться уже не нижняя, а
верхняя огибающая семейства прямых, соответствующих чистым
стратегиям 1-го игрока. Абсцисса нижней точки(пика) этой огибаю-
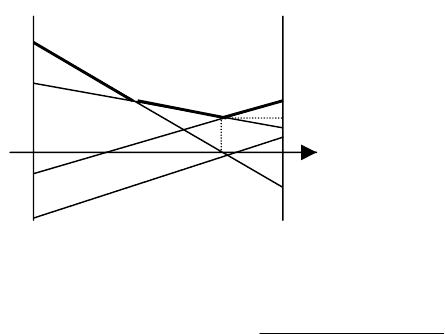
37
щей есть η
*
, т.е. оптимальная стратегия 2-го игрока; ордина та – цена
игры ν (см. рис. 2.5).
Можно решить зада-
чу, заменив знак выигрыша
на обратный, превратив
игрока 2 из
“проигрывающего” в
“выигрывающего”. В этом
случае задача m×2 решается
аналогично задаче 2×n (рис.
2.4)
Для игры формата
m×2 можно записать фор-
мулу для ξ
*
, подобную
формуле (2.30):
2i1i2i1i
1i2i
*
2221
22
hhhh
hh
−−−
−
=ξ
. (2.32)
Зная η
*
и ξ
*
, можно найти цену игры, подставляя эти значения в
(2.19).
2.7. Общие методы решения конечных игр
В общем случае решение игры n×m представляет довольно
трудную задачу, причем сложность задачи и объем необходимых для
решения вычислений резко возрастает с увеличением n и m. Однако
эти трудности не носят принципиального характера и связаны только с
очень большим объемом расчетов, который в ряде случаев может ока-
заться практически невыполнимым. Принципиальная сторона метода
отыскания решения остается при любом n и m одной и той же.
Проиллюстрируем это на примере игры 3×m. Дадим ей геом ет-
рическую интерпретацию – уже пространственную. Три наши страте-
гии
3
1
2
1
1
1
xиx,x
изобразим тремя точками на плоскости Х0У; пер-
вая лежит в начале координат (рис. 2.6), вторая и третья – на осях 0X и
0У на расстояниях 1 от начала.
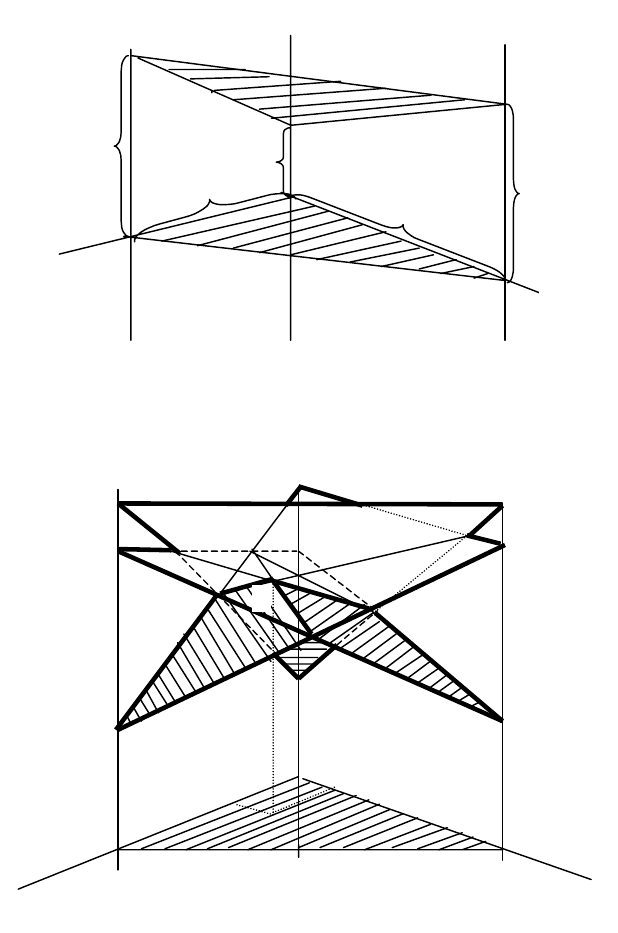
Через точки
3
1
2
1
1
1
xиx,x
проводят ся оси I-I, II-II и III-III, пер-
пендикуля рные к плоскости Х0У. На оси I-I откладыв аются выигрыши
при стратегии
1
1
x
, на осях II-II и III-III – выигрыши при cтратегиях
3
1
2
1
x,x
. Каждая стратегия противника
j
2
x
изобразится плоскостью, отсе-
кающей на осях I-I, II-II и III-III отрезки, равные выигрышам при соответ-
ствующих стратегиях
3
1
2
1
1
1
xиx,x
и ст р ат е ги и
j
2
x
.
N – точка “пика”
0
1
H
2
-H
2
η
ν
N
η
*
Рис.2.5
38
Построив таким образом все стратегии противника, мы получим
семейство плоскостей над треугольником
3
1
2
1
1
1
xиx,x
(рис. 2.7).
X
Y
I
II
II
0
y
x
3
2
x
N
3
2
x
3
2
x
2
2
x
2
2
x
2
2
x
3
1
x
1
2
x
1
2
x
1
2
x
2
1
x
1
1
x
III
I
Рис. 2.7
III
ν
Y
0
1
1
h
11
h
31
)x(
1
2
1
2
x
)x(
2
1
1
2
x
h
21
II
I
III
III
I
II
X
Рис. 2.6
)x(
3
1

39
Для этого семейства также можно построить нижнюю границу
выигрыша, как мы это делали в случае 2×m, и найти на этой границе
точку N с максимальной высотой над плоскостью Х0У. Эта высота и
будет ценой игры ν.
Частоты ξ
1
, ξ
2
, ξ
3
стратегий
3
1
2
1
1
1
xиx,x
в оптимально й
стратегии
1
X
будут определяться координатами (х, у) точки N, а
именно: ξ
2
= х; ξ
3
= y; ξ
1
= 1 – ξ
2
– ξ
3
.
Однако такое геометрическое построение даже для случая 3×m
нелегко осуществимо и требует больших затрат времени и усилий во-
ображения. В общем же случае игры оно переносится в n-мерное про-
странство и теряет всякую наглядность, хотя употребление геометри-
ческой терминологии в ряде случаев может оказаться полезным. Пр и
решении игр n×m на практике удобнее пользоваться не геометриче-
скими аналогиями, а расчетными аналитическими методами, тем бо-
лее, что для решения задачи на вычислительных машинах эти методы
единственно пригодны.
Универсальным методом решения матричных игр в смешанных
стратегиях является метод линейного программирования. Опираясь на
утверждение, что один из игроков не может улучшить свой результат,
отступая от оптимальной стратегии, если его оппонент придерживает-
ся ее, можно записать следующую систему неравенства с позиции 1-го
игрока:
)1,...,1,1(HX
T
1
ν≥
(2.33)
или в развернутой форме:
,h...hh
m1m221111
ν≥
ξ
++
ξ
+
ξ
,h...hh
m2m222112
ν≥
ξ
++
ξ
+
ξ
(2.34)
. . . . . . . . . . . . . .
.h...hh
mmn2n21n1
ν≥
ξ
++
ξ
+
ξ
Разделим неравенства на ν>0 (если ν<0, то следует перейти к
стратегически эквивалентной игре Г', для которой все h
ij
>0, а значит, и
ν>0).
,1ph...phph
m1m221111
≥+++
,1ph...phph
m2m222112
≥+++
. . . . . . . . . . . . . .
1ph...phph
mmn2n21n1
≥+++
,
где
0p
i
i
≥
ν
ξ
=
для всех
m,1i =
. (2.35)

40
Так как
∑
=
=ξ
m
1i
i
,1
то
∑
=
ν
=
m
1i
i
,
1
p
но ν – это цена игры, которую
следует максимизировать, а следовательно, следует минимизировать
линейную форму
minp...ppL
m21
→+++=
.
Таким образом, задача нахождения
*
1
Х свелась к задаче линей-
ного программирования с n ограничениями и m переменными, которая
может быть сформулирована следующим образом: определить значе-
ния переменных p
i
≥ 0, i=1,n, так, чтобы они удовлетворяли линейным
ограничениям (2.35) и при этом линейная функция
L = p
1
+p
2
+ ... +p
n
(2.36)
обращалась в минимум.
При определении оптимальной стратегии 2-го игрока
)...,,,(X
*
m
*
2
*
1
*
2
ηηη=
исходим из того, что средний проигрыш игрока
В не превосходит цены игры, какую бы чистую стратегию не применял
игрок А. То есть переменные η
1
, η
2
, ..., η
m
удовлетворяют неравенст-
вам:
a
11
·η
1
+ a
12
·η
2
+ … + a
1m
·η
m
≤ ν ,
a
21
·η
1
+ a
22
·η
2
+ … + a
2m
·η
m
≤ ν , (2.37)
. . . . . . . . . . . . . . . . .
a
n1
·η
1
+ a
n2
·η
2
+ … + a
nm
·η
m
≤ ν .
Если обознач ить q
j
= η
j
/ν, j =1, m , (2.38)
то получим систему неравенств:
a
11
·q
1
+ a
12
·q
2
+ … + a
1m
·q
m
≤ 1 ,
a
21
·q
1
+ a
22
·q
2
+ … + a
2m
·q
m
≤ 1 , (2.39)
. . . . . . . . . . . . . . . . .
a
n1
·q
1
+ a
n2
·q
2
+ … + a
nm
·q
m
≤ 1 .
Переменные q
j
, (j = 1, m) у довл етворяют условию q
1
+ q
2
+ ... + q
m
= 1/ν
(из равенства η
1
+ η
2
+ ... +η
m
=1).
Если учесть, что игрок В стремится м инимизировать гарантиро-
ванный выигрыш, то есть найти max(1/ν), игра сведется к следующей
задаче: определить значения переменных q
j
≥0, j=1, m, которые удов-
летворяют системе неравенств (2.39) и максимизируют линейную
функцию М = q
1
+ q
2
+ ... + q
m
. (2.40)
Здесь присутствуют m ограничений и n переменных.
Составив расширенные матрицы для рассмотренных задач убе-
ждаемся в следующем:
– одна матрица получилась из другой транспонированием;
– знаки неравенств поменялись на противоположные;
– экстремумы линейных функций имеют противоположный
смысл;
