Бевз Г.П., Бевз В.Г., Владімірова Н.Г. Геометрія 10-11
Подождите немного. Документ загружается.


дістають
тільки
наближені
значення
об'ємів.
значення
об'ємів
геометричних
тіл
обчислюють
формулами,
які
ми
виведемо
графах.
c;j
5250.
Бічне
ребро
прямої
призми
поділено
3
рівні
частини
і
через
точки
поділу
проведено
пло
щини,
паралельні
основі.
Знайдіть об'єми
утворених
при
цьому
многогранників,
якщо
об'єм даної
призми
V.
5260.
Знайдіть
об'єми
двох
трикутних
призм,
на
які
паралелепіпед
з
об'ємом
V
поділяється
його
діа
гональною
площиною.
5270.
Об'єм правильної
чотирикутної
призми
до
рівнює
14
дм
3
•
Знайдіть
об'єми
многогранників,
на
які
дана
призма
поділяється
двома
перпендикуляр
ними
діагональними
площинами.
528.
Висоти
двох
прямокутних
паралелепіпедів
з
рівними
основами
відносяться,
як
3 : 5.
ЯК
відно
сяться
їх
об'єми?
І:>
РОЗВ'ЯЗАННЯ.
Розглянемо
два
паралелепіпеди
із
спільною
основою
AВCD
і
висотами
АА
І
і
АА
2
(мал.
183).
Покажемо,
що
об'єми
VI
і
V
2
цИХ
парале
лепіпедів
відносяться,
як
їх
висоти, тобто
як
3 : 5.
Поділимо
ребро
АА
2
на
5
рівних
частин,
тоді
в
ребрі
АА
І
вміститься
3
такі
частини.
Площини,
про
ведені
через
точки
поділу
пара-
О2
А2
С2
----.,.
('-
......
--1",
О1'
;.г--
с
/,
,
с
,
,
DJ-_-
/
Мал.
183
160
.
EZFEZ
лельно основам
паралелепіпедів,
один
з
них
поділять
на
5,
а
дру
гий
на
3
рівних
паралелепіпеди.
Якщо
об'єм
одного
такого
парале
лепіпеда
дорівнює
V,
то
VI
=
3V,
V
2
=
5V
і
VI
: V
2
=
3V:
5V
=
3:
5.
5290.
Ребра
двох
кубів
відно
сяться,
як
1 :
3.
Як
відносяться
їх
об'єми?
Проілюструйте
це
ма
люнком.
),5300.
Обrpунтуйте
співвідношення:
"з
3
З
З
1)
1
м
=
1000
дм
; 2) 1
дм
=
1000
см
.
5310.
Скільки
кубів
з
ребром
1
дм
можна
вкласти
в
коробку,
розміри
якої
3
х
4
х
5
дм?
532.
Доведіть,
що
коли
одне
тіло
є
частиною
дру
гого,
то
об'єм
першого
тіла
менший
від
об'єму
дру
гого.
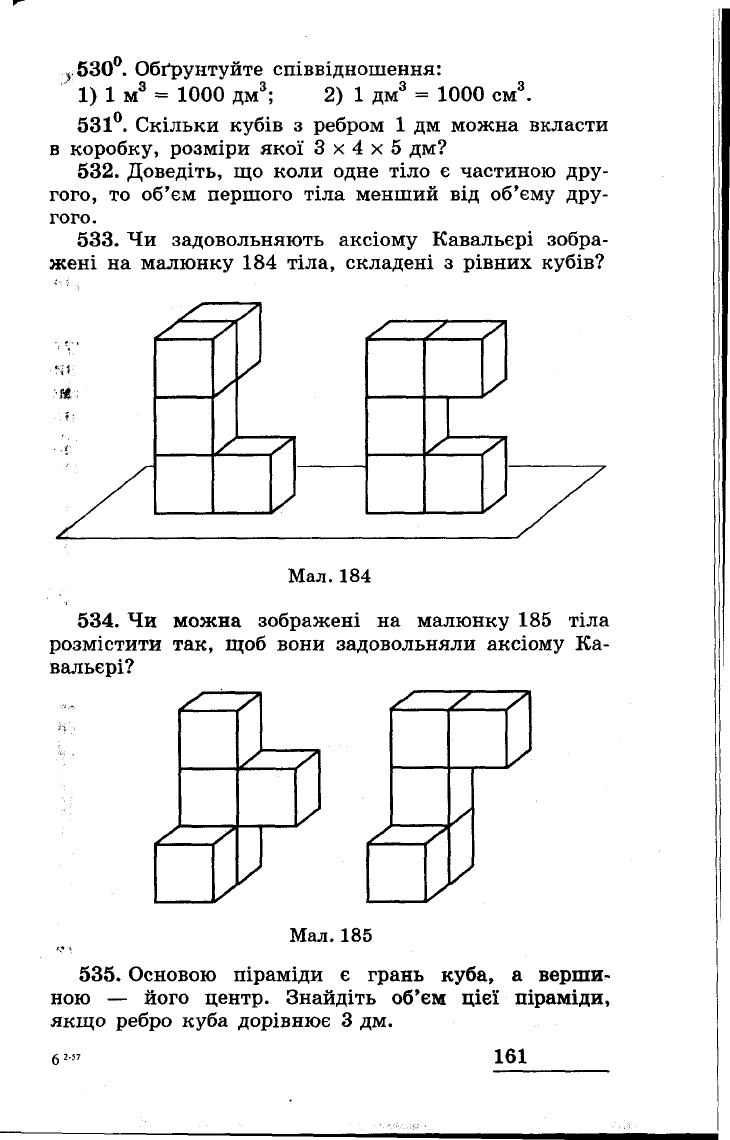
533.
Чи
задовольняють
аксіому
Кавальєрі
зобра
жені
на
малюнку
184
тіла,
складені
з
рівних
кубів?
./
/'
/' /' /'
/'
/'
';!1<'
~'i
1
V
'J't
/ /
.'
І
.,!
./ ./ ./ ./
/
/ /
/
Мал.
184
534.
Чи
можна
зображені
на
малюнку
185
тіла
розмістити
так,
щоб
вони
задовольняли
аксіому
Ка
вальєрі?
./
./
/'
1/
/' /'
V
Мал.
185
535.
Основою
піраміди
є
грань
куба,
а
верши
ною
-
його
центр.
Знайдіть
об'єм
цієї
піраміди,
якщо
ребро
куба
дорівнює
3
ДМ.
6 ,-" 161
Об'
єм
nрямокуmnого
nаралелеnіnеда
Доведемо
спочатку
лему
про
об'єми
прямокутних
паралелепіпедів.
(Лемою
називають
допоміжне
твер
дження,
яке
використовується
для
доведення
якоїсь
важливої
теореми.)
Лем
а.
Об'єми
прямокутних
паралелепіпедів
з
рів-
,
ними
основами
відносяться
як
Їх
висоти.
~
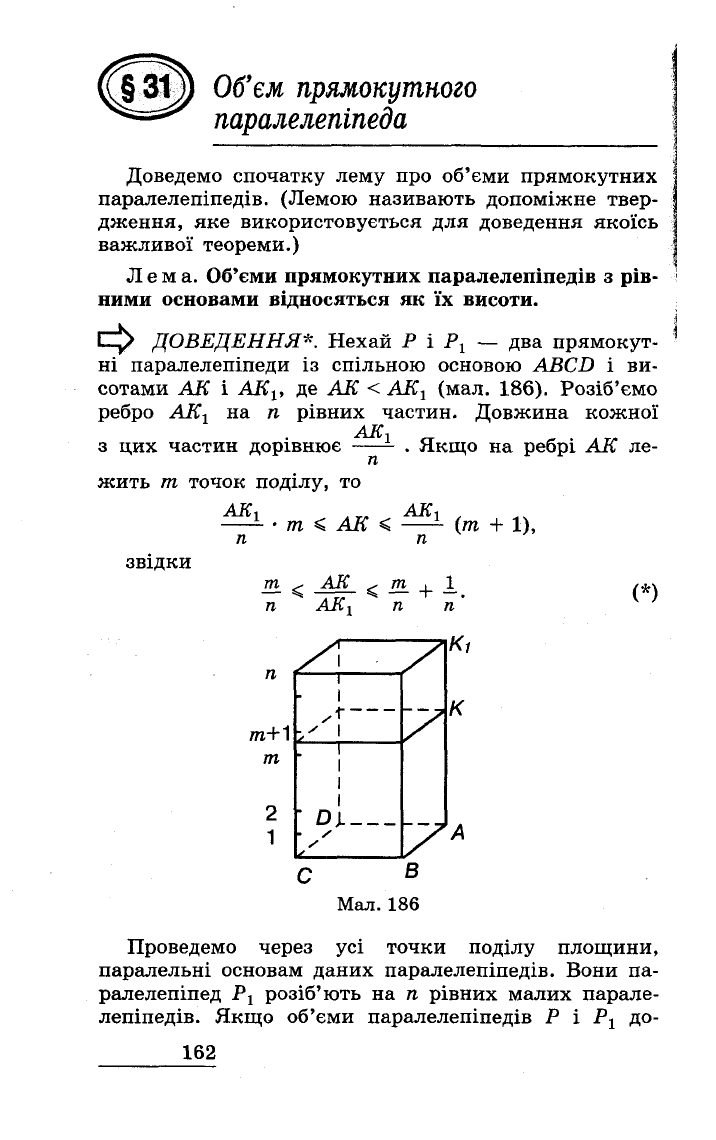
ДОВЕДЕННЯ*.
Нехай
Р
і
РІ
-
два
прямокут
ні
паралелепіпеди
із
спільною
основою
АВсп
і
ви
сотами
АК
і
АКІ'
де
АК
<
АКІ
(мал.
186).
Розіб'ємо
ребро
АКІ
на
n
рівних
частин.
Довжина
кожної
з
цих
частин
дорівнює
АКІ
.
Якщо
на
ребрі
АК
ле-
п
жить
m
точок
поділу,
то
звідки
АКІ
АКІ
--
. m
~
АК
~
--
(m
+ 1),
n n
тАКт
1
-
~
--
~
-
+-.
n
АКІ
n n
n
т+
1
I'---r--""
т
2
1
І
І
І
Dj.
__
_
"
"
с
в
Мал.
186
(*)
Проведемо
через
усі
точки
поділу
площини,
паралельні
основам
даних
паралелепіпедів.
Вони
па
ралелепіпед
РІ
розіб'ють
на
n
рівних
малих
парале
лепіпедів.
Якщо
об'єми
паралелепіпедів
Р
і
РІ
до-
162

рівнюють
відповідно
V
і
VI'
то
об'єм
одного
малого
У1
паралелепіпеда
дорівнює
n
Оскільки
парале-
лепіпед
Р
містить
m
малих
паралелепіпедів
і
міститься
в
паралелепіпеді,
складеному
з
m + 1
ма-
лих,
то
У1
У1
- • m
~
V
~
(m
+ 1),
n n
звідки
(**)
Як
видно
з
подвійних
нерівностей
(*)
і
(**),
чис
ла
L
і
АК
належать
проміжку
[ m ; m +
1]
,
У1
АК
1
n n n
тобто
відрізняються одне
від
одного не
більше,
ніж
на
1 .
Число
n
можна
взяти
як
завгодно
великим,
n
тому
1
може
як
завгодно
мало
відрізнятись
від
о.
n
А
це
можливо
тільки
тоді,
коли
АК
АК
1
•
О
ТЕОРЕМА
81.
Об'єм
прямокутного
паралеле
піпеда
дорівнює
добутку
трьох
його
вимірів.
~
ДОВЕДЕННЯ*.
Нехай
дано
довільний
прямо
кутний
паралелепіпед
з
вимірами
АВ =
а,
AD
=
Ь
і
АА
І
=
С
(мал.
187).
Побудуємо при
ЙОГО
вершині
А
l'
в
СІ
І
І
І
І
І
CJ--------
"
"
"
Мал.
187
163

пр.ямокутні
паралелепіпеди
з
вимірами
1, 1, 1
(оди
ничний
куб),
1,
1,
с
і
1,
Ь,
с
(їх
діагоналі
АЕ,
АК
і
АР).
Якщо
об'єми
цих
паралелепіпедів
дорівнюють
відповідно
1,
V
c
і
V
bc
'
а
об'єм
даного
паралелепіпе
да
V,
то за
доведеною
лемою
V
bc
Ь
-У=і'
с
Перемноживши
почленно
ці
три
рівності,
діста
немо:
V =
аЬс.
О
•
Нас
л
і
д
к
и.
1.
Нкщо
ребро
куба
дорів",ює
а,
то
його
об'єм
V =
аЗ.
2.
Об'єм
nрямокут",ого
nаралелеnіnеда
дорів",ює
добутку
площі
його
ос",ови
",а
висоту.
5360.
Розміри
цеглини
250
х
120
х
65
мм.
Знай
діть
її
об'єм.
5370.
Знайдіть
об'єм
куба,
якщо
площа
його
грані
дорівнює
Q.
5380.
Знайдіть
об'єм
правильної
чотирикутної
призми,
якщо
площа
її
основи
дорівнює
49
см
2
,
а
площа
бічної
грані
56
см
2
•
5390.
Діагональ
куба
дорівнює
d.
Знайдіть
його
об'єм.
5400.
Об'єм
куба
дорівнює
V.
Знайдіть
площу
йо
го
поверхні.
541.
Поле
прямокутної
форми
площею
5
га
зора
но на
глибину
35
см.
Скільки
кубометрів
(рунту
пе
ревернули?
5420.
Діагональ
правильної
чотирикутної
призми
дорівнює
d
і
нахилена
до
площини
основи
під
ку
том
а.
Знайдіть
об'єм
призми.
Обчисліть,
якщо
d = 37
см,
а
= 580.
54з0.
Три
свинцевих
куби
з
ребрами
1
см,
6
см
і
8
см
переплавили
в
один
куб.
Знайдіть
довжину
ребра утвореного
куба.
164

5440.
На
кожного
учня
класу
повинно
припадати
не
менш
як
6
МЗ
повітря.
На
скількох
учнів
розра
хована
класна
кімната,
розміри
якої
10
х
6
х
3,5
м?
5450.
Виміри
прямокутного
паралелепіпеда
15
дм,
36
дм
і
50
дм.
Знайдіть
довжину
ребра
куба
такого
самого
об'єму.
546.
Якщо
кожне
ребро
куба
збільшити
на
3
см,
то
його
об'єм
збільшиться
на
513
см
3
•
Знайдіть
дов
жину
ребра
куба.
547.
Площі
трьох
нерівних
граней
прямокутного
паралелепіпеда
дорівнюють
81'
82
і
8з.
Знайдіть
йо
го
об'єм.
t::>
РОЗВ'ЯЗАНня.
Якщо
виміри
паралелепіпеда
х,
у,
г,
то
ху
=
81>
хг
=
82'
уг
=
8з.
Перемноживши
почленно
ці
рівності,
дістанемо
х
2
у
2
г
2
=
81828з,
звідки
V =
хуг
=
~
81828з.
Відповідь.
~
81828з.
548.
Сторони
основи
прямокутного
паралелепіпе
да
дорівнюють
а
і
Ь,
а
його
діагональ
нахилена
до
площини
основи
під
кутом
а.
Знайдіть
об'єм
пара
лелепіпеда.
549.
Знайдіть
об'єм
правильної
чотирикутної
приз
ми,
якщо
її
діагональ
дорівнює
d,
а
діагональ
бічної
грані
d
1
•
550.
Знайдіть
об'єм
правильної
чотирикутної
приз
ми,
якщо
її
діагональ
дорівнює
d
і
з
бічною
гранню
утворює
кут
<р.
551.
Знайдіть
об'єм
прямокутного
паралелепіпеда,
якщо
два
його
виміри
а
і
Ь,
а
радіус
описаної
кулі
г.
552.
В
основі
прямої
призми
лежить
прямокут
ник.
Діагональ
призми
утворює
з
площиною
основи
кут
а,
а
діагональ
однієї
з
бічних
граней
дорівнює
l
і
нахилена
до
площини
основи
під
кутом
<р.
Знай
діть
об'єм
призми.
Обчисліть,
якщо
l =
2.J6
см,
а
= 450,
<р
= 600.
165
@
Об'єм
nрuзмu
.
ТЕОРЕМА
32.
Об'
єм призми
дорівнює
добутку
площі
ії
основи
на
висоту:
Yn=
Sh.
r:::>
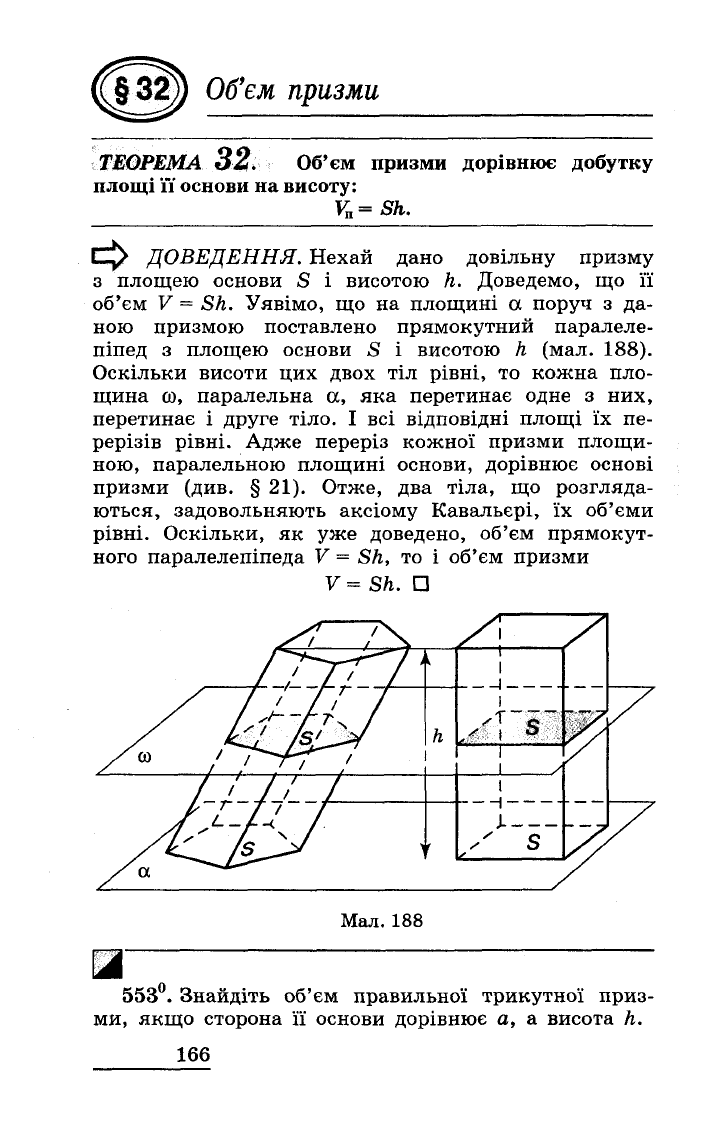
ДОВЕДЕННЯ.
Нехай
дано
довільну
призму
з
площею
основи
S
і
висотою
h.
Доведемо,
що
її
об'єм
V = Sh.
Уявімо,
що
на
площині
а
поруч
з
да
ною
призмою
поставлено
прямокутний
паралеле
піпед
з
площею
основи
S
і
висотою
h
(мал.
188).
Оскільки
висоти
цих
двох
тіл
рівні,
то
кожна
пло
щина
0),
паралельна
а,
яка
перетинає
одне
з
них,
перетинає
і
друге
тіло.
І
всі
відповідні
площі
їх
пе
рерізів
рівні.
Адже
переріз
кожної
призми
площи
ною,
паралельною
площині
основи,
дорівнює
основі
призми
(див.
§ 21).
Отже,
два
тіла,
що
розгляда
ються,
задовольняють
аксіому
Кавальєрі,
їх
об'єми
рівні.
Оскільки,
як
уже
доведено,
об'єм
прямокут
ного
паралелепіпеда
V = Sh,
то
і
об'єм
призми
V=
Sh.
О
Мал.
188
~
55з0.
Знайдіть
об'єм
правильної
трикутної
приз
ми,
якщо
сторона
її
основи
дорівнює
а,
а
висота
h.
166

5540.
В
основі
прямої
призми
-
прямокутний
трикутник
З
катетами
3
см
і
4
см.
Більша
бічна
грань
-
квадрат.
Знайдіть
об'єм
призми.
5550.
Діагональ
грані
правильної
трикутної
приз
ми
дорівнює
d
і
нахилена
до
сторони
основи
під
ку
том
а.
Знайдіть
об'єм
призми.
5560.
Площа
основи
призми
Q,
бічне
ребро
дорів
нює
І
і
нахилене
до
площини
основи
під
кутом
а.
Знайдіть
об'єм
призми.
5570.
Сторони
основи
паралелепіпеда
дорівнюють
6
дм
і
8
дм,
кут
між
ними
450.
Бічне
ребро
дорів
нює
7
дм
і
нахилене
до
площини
основи
під
кутом
450.
Знайдіть
об'єм
паралелепіпеда.
5580.
Дві
грані
паралелепіпеда
-
ромби
із
сторо
ною
а
і
кутом
а,
решта
граней
-
квадрати.
Знай
діть
об'єм
паралелепіпеда.
5590.
Переріз
залізничного
насипу має
вигляд
трапеції
з
основами
18
м
і
8
м
і
висотою
3
м.
Знайді
ть
об'
єм
1
км
такого
насипу.
560.
У
правильній
шестикутнlИ
призмі
площа
найбільшого
діагонального
перерізу
4
см
2
,
а
від
стань
між
протилежними
бічними
гранями
4
см.
Знайдіть
об'єм
призми.
561.
Площа
основи
прямої
трикутної
призми
до-
о
24 2
о
б'
u 3 2 4 2
рІВНЮЄ
см,
а
ПЛОЩІ
ІЧНИХ
гранеи
см,
см
і
5
см
2
•
Знайдіть
об'єм
призми.
562.
Знайдіть
об'єм
правильної
п'ятикутної
приз
ми,
кожне
ребро
якої
дорівнює
а.
563.
Кожне
ребро
прямого
паралелепіпеда
дорів
нює
1
см, а
одна
з
його
діагоналей
2
см.
Знайдіть
об'єм.
564.
Намалюйте
довільну
трикутну
призму.
Побу
дуйте
її
переріз
площиною,
яка
проходить
через
бічне
ребро
і
ділить
її
на
дві
частини,
об'єми
яких
відносяться,
як
1 : 2.
565.
Основою
призми
є
правильний
трикутник
із
стороною
а.
Одна
з
бічних граней
перпендикулярна
до
площини
основи
і
є
ромбом
з
гострим
кутом
а.
Знайдіть
об'єм
призми.
Обчисліть,
якщо
а
=
17
см,
а
= 650.
167

566.
Основою
призми
є
правильний
трикутник
АВС
із
стороною
а.
Вершина
А
1
проектується
в
центр
нижньої
основи,
а
ребро
АА
1
утворює
з
площиною
ос
нови
кут
а.
Знайдіть
об'єм
призми.
Обчисліть,
якщо
а
=
25,3
см,
а
= 68012'.
Мал.
189
І:>
РОЗВ'ЯЗАННЯ.
Задачу
за
довольняє
призма
АВСА
1
В
1
С
1
,
у
якої
О
центр
правильного
Д
АВС,
А
1
О -
висота
призми,
L
А1АО
=
а
(мал.
189).
Об'єм
призми
знаходимо
за
формулою
V = Sh,
де
S -
площа
її
основи,
h -
висота.
Оскільки
а
2
JЗ
Д
АВС
правильний,
то
S =
-4-'
З
прямокутно
го
трикутника
А1АО
знаходимо
висоту
призми:
ОА
=
Jз'
h =
Ар
=
ОА
.
tg
а
=
Jз
tg
а.
Отже,
шуканий
об'єм
призми
а
2
JЗ
а
аЗ
V =
-4-
.
J3
tg
а
= 4
tg
а.
Якщо
а
=
25,3
і
а
= 68012',
то
V =
25~3З
•
tg
68,20
:::::
10119.
З
Відповідь.
V =
а
4
tg
а;
V:::::
10,1
дм
З
•
567.
Сторона
основи
прямого
паралелепіпеда
дорівнює
а.
Через
неї
і
протилежну
ЇЙ
сторону
верхньої
основи
проведено
переріз
під
кутом
а
до
площини
основи.
Площа
перерізу
дорівнює
S.
Знай
діть
об'єм
паралелепіпеда.
568.
Основа
прямого
паралелепіпеда
-
ромб.
Од
на
з
діагоналей
паралелепіпеда
дорівнює
d
і
нахи
лена
до
площини
основи
під
кутом
а;
друга
-
під
кутом
~.
Знайдіть
об'єм
паралелепіпеда.
168
569.
Знайдіть
об'єм
прямого
паралелепіпеда,
сто
рона
основи
якого
дорівнює
а,
а
радіус
вписаної
кулі
r.
570.
у
похилій
трикутній
призмі
площа
OДНlЄl
з
бічних
граней
Q,
а
відстань
від
її
площини
до
про
тилежного
бічного
ребра
m.
Знайдіть
її
об'єм.
571.
Знайдіть
об'єм
похилої
призми,
якщо
її
бічне
ребро
дорівнює
[,
а
площа
перерізу,
який
перетинає
всі
бічні
ребра
і
перпендикулярний
до
них,
Q.
572.
Знайдіть
об'єм
правильної
восьмикутної
приз
ми,
кожне
ребро
якої
має
довжину
а.
\.
8
Об'єм
nіра.мід_и
______
_
Лем
а.
Трикутні
піраміди
з
рівними
площами
основ
і
рівними висотами
мають
рівні
об'єми.
с:>
ДОВЕДЕННЯ.
Розглянемо
дві
трикутні
піра
міди
РАВС
і
Р
1
А
1
В
1
С
1
,
кожна
з
яких
має
площу
ос
нови
S
і
висоту
h.
Розмістимо
їх
основи
в
одній
площині
а
(мал.
190).
Оскільки
висоти
обох
пірамід
рівні,
то
кожна
січна
площина
0),
паралельна
а,
пе
ретинаючи
одну
з
пірамід,
перетинає
і
другу.
Нехай
Мал.
190
169
