Бевз Г.П., Бевз В.Г., Владімірова Н.Г. Геометрія 10-11
Подождите немного. Документ загружается.

336.
А
і
В -
точки
на
ребрі
двогранного
кута
міри
сх,
АС
і
BD
-
перпендикуляри
до
ребра,
про
ведені
у
різних
гранях.
Знайдіть
відстань
CD,
якщо
АВ
=
а,
АС
=
Ь
і
BD
=
с.
І:>
РОЗВ'ЯЗАНня.
Нехай
АК
11
BD
і
АК
=
BD
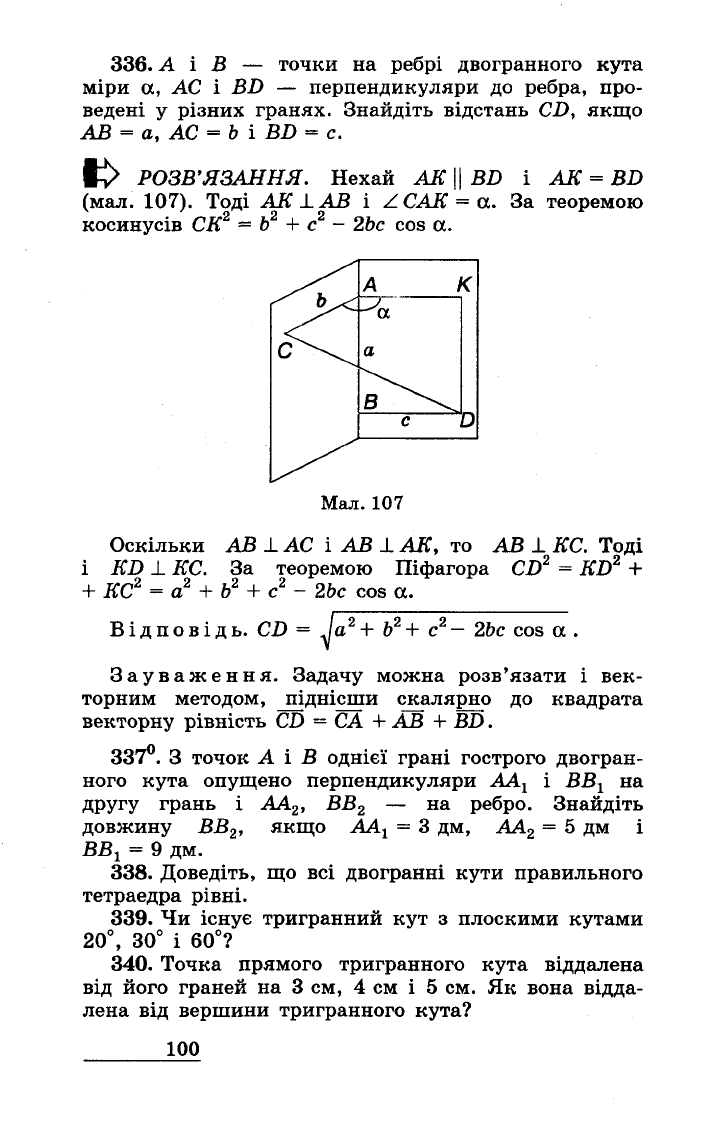
(мал.
107).
Тоді
АК
1. АВ
і
L
САК
=
сх.
За
теоремою
косинусів
ск
2
=
ь
2
+
с
2
-
2Ьс
cos
сх.
А
К
D
Мал.
107
Оскільки
АВ 1.
АС
і
АВ
1.
АК,
то
АВ
1.
КС.
Тоді
і
KD
1.
КС.
За
теоремою
Піфагора
CD
2
=
KD
2
+
+
кс
2
=
а
2
+
ь
2
+
с
2
-
2Ьс
cos
сх.
Відповідь.
CD
=
~a2+
ь
2
+
с
2
-
2Ьс
cos
сх.
Зауваження.
Задачу
можна
розв'язати
і
век
торним
методом,
піднісши
скалярно
до
квадрата
векторну
рівність
CD =
СА
+ АВ +
BD.
3370.
З
точок
А
і
В
однієї
грані
гострого
двогран
ного
кута
опущено
перпендикуляри
АА
1
і
ВВІ
на
другу
грань
і
АА
2
,
ВВ
2
-
на
ребро.
Знайдіть
довжину
ВВ
2
,
якщо
АА
1
= 3
дм,
АА
2
= 5
дм
і
ВВІ
= 9
дм.
338.
Доведіть,
що
всі
двогранні
кути
правильного
тетраедра
рівні.
339.
Чи
існує
тригранний
кут
з
плоскими
кутами
200,
300
і
60
0
?
340.
Точка
прямого
тригранного
кута
віддалена
від
його
граней
на
3
см,
4
см
і
5
см.
Як
вона
відда
лена
від
вершини
тригранного
кута?
100

Мал.
108
1:>'
РОЗВ'ЯЗАННЯ.
Нехай
ОХ,
ОУ,
OZ
-
ребра
прямого
тригранного
кута,
а
його
точка
А
віддалена
від
його
граней
на
відстані
АК
=
3,
АР
=
4,
АТ
= 5
(мал.
108).
Якщо
площина
АРК
перетинає
ребро
ОУ
у
точці В,
то
АРВК
і
АВОТ
-
прямокутники
(до
ведіть).
Отже,
ОА
2
=
АВ
2
+
ов
2
=
АР
2
+
АК
2
+
Ат
2
=
=
42+
з2+
52
= 50.
Відповідь.
5.J2
см.
341.
На
ребрах
ОА,
ОВ,
АС
прямого
тригранного
кута
позначено
довільні
точки
А,
В,
С.
Доведіть,
що
трикутник
АВС
гострокутний.
342.
Кожний
плоский
кут
тригранного
кута
до
рівнює
600.
Знайдіть
кут
між
його
ребром
і
бісект
рисою
протилежного
плоского
кута.
343.
Скільки
існує
різних
чотиригранних
кутів,
всі
плоскі
кути
яких
мають
по
40
0
?
344.
Чи
існує
опуклий
ЧОТИРИГ,Rанний
кут
з
плос
кими
кутами
500, 700, 1100
і
140
?
345.
Учень
говорить:
«Кути
бувають
плоскі,
дво
гранні
і
многогранні».
Чи
це
правильно?
В
і
дп
о в
і
Д
ь.
Ні,
неправильно.
Кутом
називаєть
ся
частина
площини,
обмежена
двома
променями
із
спільною
вершиною.
Жоден
з
двогранних
чи
много
гранних
кутів
не
підходить
під
це
означення,
тому
не
є
кутом
.
•
346.
Практичне
завдання.
1)
Зробіть
з
цуп
кого
паперу модель
поверхні
двогранного
кута,
на
кресліть
будь-який
його
лінійний
кут
і
продемонст
руйте,
як
змінюється
двогранний
кут
із
зміною
йо
го
лінійного
кута.
2)
Зробіть
модель
поверхні
тригранного
кута.
101

@
Геометриті
тіла
і
многогранники
Кожний
двогранний
чи
многогранний
кут
-
це
об'єднання
деякої
нескінченної
просторової
області
і
її
поверхні.
Об'єднання
скінченної
просторової
об
ласті
і
її
поверхні
називають
геометричним
тілом.
Щоб
не
ускладнювати
виклад,
ми
не
наводимо
стро
гих
означень
понять
«просторова
область»
і
«поверх
ня
просторової
області.),
а
обмежимось
прикладами.
Нехай
маємо
деякий
куб.
Його
поверхня
скла
дається
з
шести
квадратів.
Усі
точки
куба,
які
не
належать
його
поверхні,
становлять
скінченну
про
сторову
область.
Скінченну
-
бо
відстань
між
її
найвіддаленішими
точками
не
перевищує
деякої
скінченної
відстані.
Отже,
куб
є
об'єднанням
певної
скінченної
просторової
області
і
її
поверхні.
Те
саме
можна
сказати
про
будь-який
паралелепіпед,
тетра
едр,
циліндр
і
т.
п.
Кожна
з
цих
фігур
-
геомет
ричне
тіло.
І
будь-яка
фігура
у
формі
картоплини
або
бублика
-
теж
геометричне
тіло.
Кожне
геомет
ричне
тіло
-
це
фігура
(множина
точок),
яка
скла
дається
з
однієї
скінченної
просторової
області,
усієї
її
поверхні
і
не
має
ніяких
інших
точок.
Напри
клад,
об'єднання
двох
кубів
з
одним
спільним
реб
ром
(мал.
109,
а)
-
не
геометричне
тіло,
бо
містить
дві
просторові
області
(відкиньте
поверхню
ЦІЄl
фігури,
і
дві
її
просторові
області
виявляться
не
зв'язаними).
І
куб
з
відрізком
(мал.
109,
б)
-
не
геометричне
тіло,
бо
всі
точки
відрізка,
крім
одного
кінця,
не
належать
ні
поверхні
куба,
ні
його
про
сторовій
області.
Оскільки,
крім
геометричних
тіл,
у
геометрії
ніяких
інших
тіл
не
розглядають,
далі
ми
їх
буде
мо
називати
тілами.
а
Мал.
109
102

.l!'d. /
~[Q
/І
/
~
І
/
/'1
CJ
/
І
IZ::J
l/
Мал.
110
Мал.
111
Означення.
Многогранником
називається
тіло,
поверхня
якого
складається
із
скінченної
кількості
.многокутників.
Многокутники,
які
обмежують
многогранник,
на
зивають
гранями,
їх
сторони
-
ребрами,
а
кінці
ре
бер
-
вершинами
многогранника.
Відрізок,
який
сполучає
дві
вершини,
що
не
належать
одній
гра
ні,
-
діагональ
многогранника.
Бувають
многогранники
з
многогранними
(,отво
рами».
Таку
форму
мають,
наприклад,
залізобетонні
стіни
з
отворами
для
вікон
(мал.
110),
столярні
ви
роби
і
окремі
Їх
деталі
(мал.
111).
Деякі
грані
подібних
многогранників
мають
много
кутні
(.
отво
ри>}.
Зрозуміло,
що
кожний
з
таких
многогран
ників
-
фігура неопукла.
Але
й многогранники
без
отворів
можуть
бути
неопуклими
(мал.
112).
Най
простіші
многогранники
-
опуклі.
Опуклий
много
гранник
розміщений
з
одного
боку
від
площини
кожної
його
грані.
Усі
грані
опуклого
многогранни
ка
-
опуклі
многокутники.
Якщо
поверхню
многогранника
розрізати
по
кількох
його
ребрах
і
розпластати
на
площині,
дістанемо
розгортку
даного
многогранника.
На
ма
люнку
113
зображено
дві
різні
розгортки
куба.
~
І І
Мал.
112
Мал.
113
103

Мал.
114
Площа
поверхні
многогранни-
ка
-
це
сума
площ
усіх
його
гра
ней.
Вона
дорівнює
площі
розгорт
ки
даного
многогранника.
Якщо
принаймні
дві
точки
мно
гогранника
лежать
по
різні
боки
від
площини,
говорять,
що
площи
на
перетинає
многогранник.
У
цьо
му
разі
її
називають
січною
nЛОЩU
ною.
Фігура,
яка
складається
з
усіх
точок,
спільних
для
многогранника
і
січ
ної
площи
ни,
-
nереріз
многогранника
даною
площиною
(мал.
114).
Кожний
пере
рі
з
опуклого
многогранни
ка
-
опуклий
многокутник.
3470.
Намалюйте
многогранник,
який
має
4
гра
ні.
Скільки
ребер
і
вершин
він
має?
Як
називається
такий
многогранник?
3480.
Намалюйте
многогранник,
який
має:
1) 5
граней
і
5
вершин;
2) 5
граней
і
6
вершин.
349.
Чи
існує
многогранник,
відмінний
від
тетра
едра,
всі
грані
якого
-
трикутники?
350.
Многогранник
має
9
ребер.
Доведіть,
що
йо
го
гранню
не
може
бути п'ятикутник.
І:>
РОЗВ'ЯЗАНня.
Якщо
многогранник
має
п'
ятикутну
грань,
то
кожна
її
вершина
є
вершиною
деякого
многогранного
кута
і
з
неї
виходить
не
менше
трьох
ребер.
Такий
многогранник
має
10
або
більше
ребер.
Тому
якщо
многогранник
має
тільки
9
ребер, він
не
може
мати
п'ятикутної
грані.
3510.
Намалюйте
розгортку
правильного
тетраед
ра,
ребро
якого
дорівнює
2
см.
Знайдіть
площу
роз
гортки.
3520.
Площа
поверхні
правильного
тетраедра
до
рівнює
36
см
2
•
Знайдіть
довжину
його
ребра.
35з0.
Площі
трьох
граней
паралелепіпеда
дорів
нюють
2
м
2
,
3
м
2
і
4
м
2
•
Знайдіть
площу
його
по
верхні.
104

354.
Знайдіть
площу
поверхні
прямокутного
па
ралелепіпеда,
якщо
одне
його
ребро
доріВIJЮЄ
а,
а
площі
прилеглих
до
нього
граней
81
і
82'
355.
Якщо
від
куба
ABCDA
1
B
1
C
1
D
1
відрізати
тетраедр
A
1
AВ
1
D
1
,
залишиться
многогранник
AВCDD
1
B
1
C
1
•
Скільки
граней,
ребер
і
вершин
він
матиме?
Знайдіть
площу
його
найбільшої
грані,
як
що
АВ
=
а.
356.
На
ребрах
прямого
тригранного
кута
з
вер
шиною
О
відкладено
відрізки
ОА
=
ОВ
=
ОС
=
а
і
через
точки
А,
В,
С
проведено
площину.
Знайдіть
площу
поверхні
утвореного
многогранника.
357.
Площі
трьох
граней
прямокутного
парале
лепіпеда
дорівнюють
10
см
2
,
15
см
2
і
24
см
2
•
Знай
діть
довжини
його
ребер.
358.
Знайдіть
площу
поверхні
тетраедра
AВCD,
якщо
АС
=
СВ
=
BD
=
DA
= DC =
а
і
L
АСВ
=
'Р.
Об
числіть,
якщо
а
=
1,2
м,
q>
= 500 .
•
359.
Практичне
завдання.
Виріжте
з
папе
ру
розгортку:
1)
тетраедра;
2)
прямокутного
парале
лепіпеда.
8
Прu_з_Мu
_______
_
Означення.
ПРU3МQЮ
називається
многогранник,
у
якого
дві
грані
-
рівні
n-кутники,
а
решта
n
граней
-
паралелограми.
Рівні
n-кутники,
про
які
йдеться
в
цьому
озна
ченні,
називають
основами
призми.
Їх
відповідні
сторони
попарно
рівні
і
паралельні.
Всі
грані
приз
ми,
які
не
е
основами,
називають
бічними
гранями.
Бічними
ребрами
призми
називають
усі
її
ребра,
які
не
є
сторонами
основ.
Усі
бічні
ребра
призми
рівні
і
паралельні.
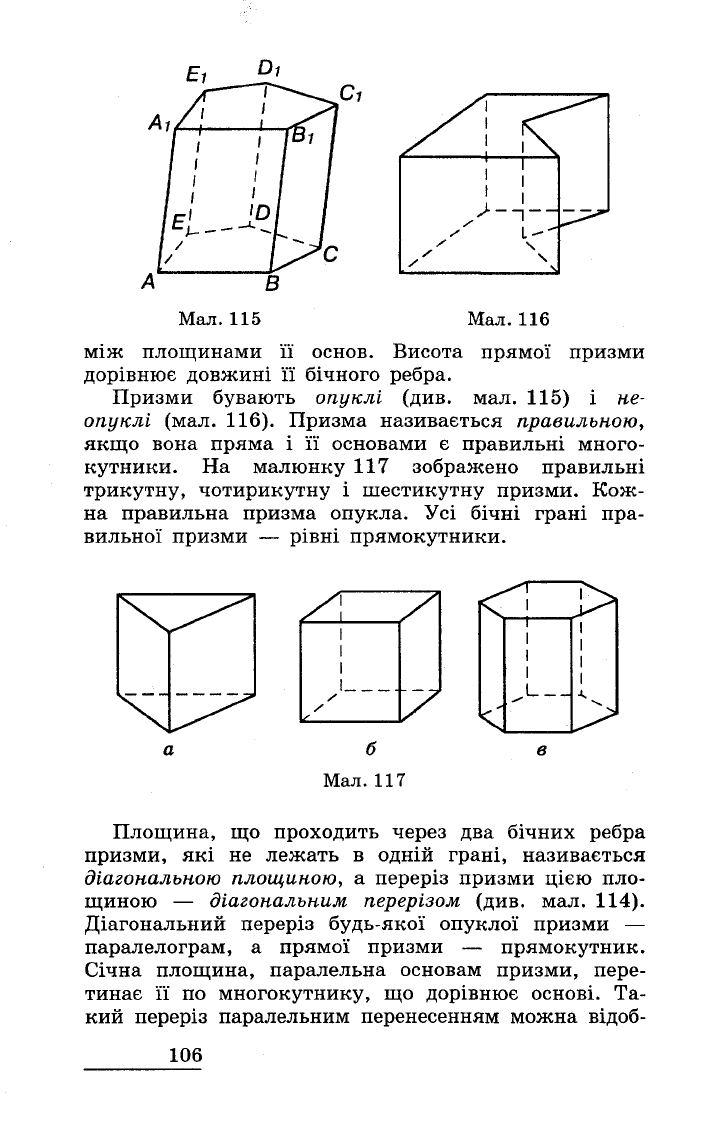
На
малюнку
115
зображено
п'ятикут
ну
призму
з
основами
AВCDE
і
A
1
B
1
C!D!E!
і
бічни
ми
ребрами
АА!, ВВ!,
ССр
DD!,
ЕЕ!.
Призма
називається
прямою,
якщо
її
бічні
ребра
перпендикулярні
до
площини
основи.
Всі
інші
призми
-
nохилі.
Кожна
бічна
грань
прямої
приз
ми
-
прямокутник.
Висота
призми
-
відстань
105
А
,
,
, ,
, ,
Е'
...іР
J---
-
/
/
Мал.
115
./
./
./
./
./
І І
І
І
).-..,-
L-
,
,
Мал.
116
між
площинами
11
основ.
Висота
прямої
призми
дорівнює
довжині
її
бічного
ребра.
Призми
бувають
опуклі
(див.
мал.
115)
і
не
опуклі
(мал.
116).
Призма
називається
правильною,
якщо
вона
пряма
і
її
основами
є
правильні
много
кутники.
На
малюнку
117
зображено
правильні
трикутну,
чотирикутну
і
шестикутну
призми.
Кож
на
правильна
призма
опукла.
Усі
бічні
грані
пра
вильної
призми
-
рівні
прямокутники.
а
б
Мал.
117
в
Площина,
що
проходить
через
два
бічних
ребра
призми,
які
не
лежать
в
одній
грані,
називається
діагональною
nлощиною,
а
переріз
призми
цією
пло
щиною
-
діагональним
nерерізом
(див.
мал.
114).
Діагональний
переріз
будь-якої
опуклої
призми
-
паралелограм,
а
прямої
призми
-
прямокутник.
Січна
площина,
паралельна
основам
призми,
пере
тинає
її
по
многокутнику
,
що
дорівнює
основі.
Та
кий
переріз
паралельним
перенесенням
можна
відоб-
106
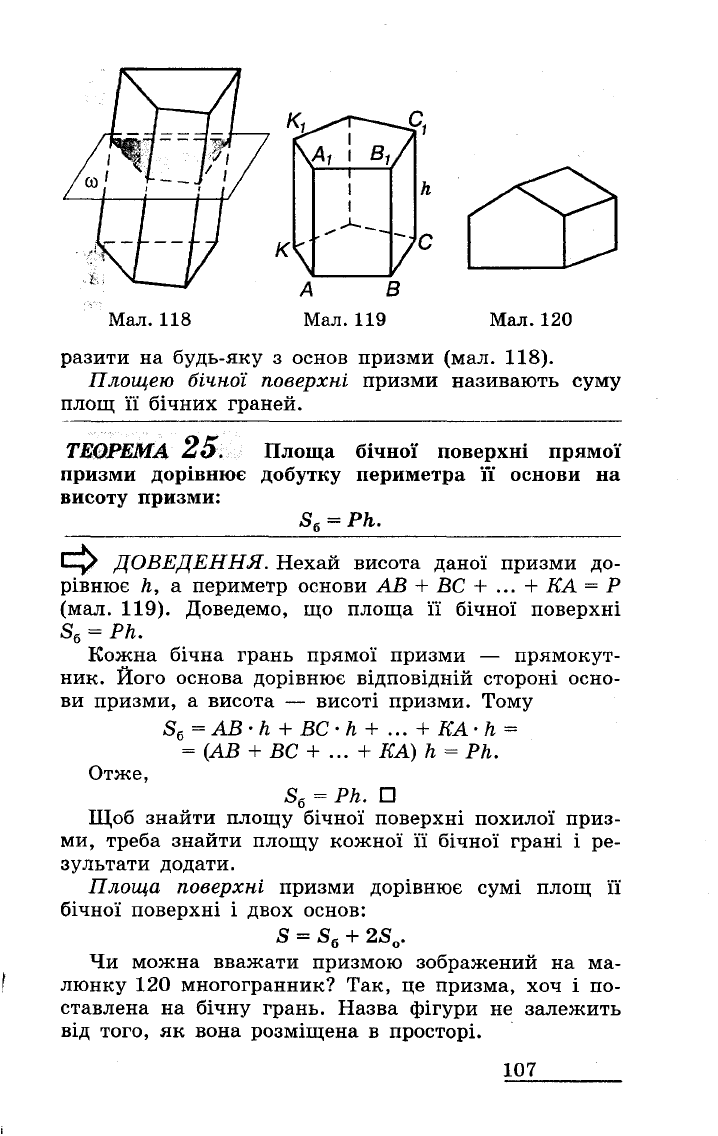
Мал.
118
Мал.
119
Мал.
120
разити
на
будь-яку
з
основ
призми
(мал.
118).
Площею
бічної
поверхні
призми
називають
суму
площ
її
бічних
граней.
ТЕОРЕМА
25.
Площа
бічної
поверхні
прямої
призми
дорівнює
добутку
периметра
іТ
основи
на
висоту
призми:
с:::>
ДОВЕДЕННЯ.
Нехай
висота
даної
призми
до
рівнює
h,
а
периметр
основи
АЕ
+
ВС
+
...
+
КА
=
Р
(мал.
119).
Доведемо,
що
площа
її
бічної
поверхні
Sб
=
Ph.
Кожна
бічна
грань
прямої
призми
-
прямокут
ник.
Його
основа
дорівнює
відповідній
стороні
осно
ви
призми,
а
висота
-
висоті
призми.
Тому
Sб
=
АЕ
. h +
ВС,
h + ... +
КА'
h =
=
(АЕ
+
ВС
+ ... +
КА)
h = Ph.
Отже,
Sб
= Ph.
О
Щоб
знайти
площу
бічної
поверхні
похилої
приз
ми,
треба
знайти
площу
кожної
її
бічної
грані
і
ре
зультати
додати.
Площа
поверхні
призми
дорівнює
сумі
площ
її
бічної
поверхні
і
двох
основ:
S =
Sб
+
2S
o
'
Чи
можна
вважати
призмою
зображений
на
ма
люнку
120
многогранник?
Так,
це
призма,
хоч
і
по
ставлена
на
бічну
грань.
Назва
фігури
не
залежить
від
того,
як
вона
розміщена
в
просторі.
107

360.
Чи
існує
призма,
яка
має
рівно
100
ребер?
361.
Доведіть,
що
n-кутна
призма
має
n + 2
гра
ні,
3n
ребер
і
2n
вершин.
362.
Скільки
діагоналей
і
діагональних
площин
має
опукла
семикутна
призма?
363.
Знайдіть
градусну
міру
двогранного
кута
при
бічному
ребрі
правильної
п'ятикутної
призми.
3640.
Бічне
ребро
призми
дорівнює
1
і
нахилене
до
площини
основи
під
кутом
а.
Знайдіть
висоту
призми.
3650.
Чи
рівні
діагональні
перерізи
правильної
чотирикутної
призми?
А
правильної
п'ятикутної?
3660.
Висота
правильної
чотирикутної
призми
до
рівнює
h,
а
сторона
основи
а.
Знайдіть:
а)
площу
її
поверхні;
б)
діагональ
призми.
3670.
Діагональ
правильної
чотирикутної
призми
дорівнює
d
і
нахилена
до
площини
основи
під
ку
том
<р.
Знайдіть
площу:
а)
діагонального
перерізу;
2)
бічної
поверхні
призми.
368.
Знайдіть
площу
діагонального
перерізу
пра
вильної
чотирикутної
призми,
висота
якої
дорівнює
10
см,
а
площа
основи
144
см
2
•
369.
Площа
поверхні
правильної
чотирикутної
призми
40
см
2
,
а
бічної
поверхні
32
см
2
•
Знайдіть
висоту
призми.
3700.
Три
грані
призми
-
квадрати
зі
стороною
2
см,
а
дві
інші
-
трикутники.
Накресліть
цю
призму
і
її
розгортку.
3710.
11
прямій
трикутній
призмі
всі
ребра
рівні.
Площа
її
бічної
поверхні
дорівнює
27
см
2
•
Знайдіть
площу
основи.
372.
Площа
діагонального
перерізу
правильної
чотирикутної
призми
дорівнює
S.
Знайдіть
площу
її
бічної
поверхні.
373.
Діагональ
бічної
грані
правильної
трикутної
призми
дорівнює
1
і
нахилена
до
площини
основи
під
кутом
а.
Знайдіть
площу
бічної
поверхні
приз
ми.
Обчисліть,
якщо
І
=
28
см,
а
=
5з0.
108

t>
РОЗВ'ЯЗАННЯ.
Нехай
приз
ма
АВСА
1
В
1
С
1
правильна,
а
діаго
наль
В
1
А
її
бічної
грані
має
довжину
[
(мал.
121).
Сторона
основи
ВА -
проекція
цієї
діаго
налі
на
площину
основи,
тому
L
В
1
АВ =
а.
Площа
бічної
поверхні прави
льної
трикутної
призми
S =
3ah,
де
а
-
сторона
основи,
а
h -
А
Мал.
121
висота
призми.
3
прямокутно
го
l:::.
В
І
АВ
знаходимо:
а
=
АВ
= l
сов
а,
h =
ВІ
В
= l
віп
а.
Отже,
~
S = 3[ cos
а
. [
sin
а
= 1,5
[2
sin
2а
.
. r
flри
даних
числових
значеннях
.:
S = 1,5 . 282
sin
1060 z 1130.
Відповідь.
S = 1,5 l2
sin
2а;
S
""
11,3
дм
2
•
374.
Через
середини
двох
сторін
основи
правиль
ної
трикутної
призми
під
кутом
а
до
основи
прове
дено
площину,
яка
перетинає
два
бічних
ребра.
Знайдіть
площу
перерізу
,
якщо
сторона
основи
дорівнює
а.
Обчисліть,
якщо
а
=
15,7
см,
а
= 300.
375.
Дано
правильну
шестикутну
призму,
кожне
ребро
якої
дорівнює
а.
Через
дві
протилежні
сторо
ни
основ
побудуйте
переріз
цієї
призми
і
знайдіть
його
площу.
376.
Побудуйте
переріз
три
кутної
призми
АВСАІВІС
І
площи
ною,
яка
проходить
через
верши
ни
А,
В
і
середину
ребра
АР!.
377,
Дано
чотирикутну
призму
AВCDA!B!Cp!
і
на
її
бічних
реб
рах
точки
КЕ
ВВ!,
РЕ
DD!,
Опишіть
за
малюнком
122,
як
можна
побудувати
переріз
даної
призми
площиною,
що
прохо
дить
через
точки
К.
Р,
СІ'
N
Мал.
122
109
