Bennett A.F. Inverse Modeling of the Ocean and Atmosphere

Подождите немного. Документ загружается.

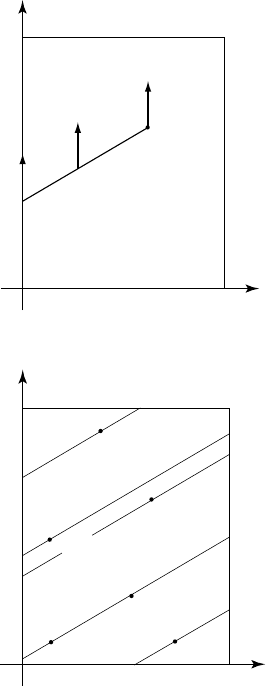
1.5 Regularity of the inverse estimate 27

, t

)

-c

-1

Figure 1.5.1 Support of

(x , t ). The arrows (the

delta functions) are normal

to the page.

, t

)

, t

)

, t

)

, t

)

, t

)

, t

)

Figure 1.5.2 Support of

singularities in

u(x, t).

subject to the initial and boundary conditions

u = I +

ı = I + W

−1

λ,

u = B +

b = B + cW

−1

λ. (1.5.6)

So our estimates of

f ,

ı and

b are singular. There is neither dispersion nor diffusion

in our “toy” ocean dynamics, so

u is also singular: see Fig. 1.5.2. This is hardly a

satisfactory combination of dynamics and data!

Exercise 1.5.1

Express r

and

u using the Green’s function γ . 

1.5.3

Nondiagonal weighting: kernel inverses of weights

We want the data to inﬂuence the circulation at remote places and times, so we should

give weight to products of residuals at remote places and times. We therefore generalize

28 1. Variational assimilation

the penalty functional (1.2.9) to

J [u] =



dy f (x, t)W

(x, t, y, s) f (y, s)



dy i(x)W

(x, y)i(y) +



ds b(t)W

(t, s)b(s)



l=1



m=1



. (1.5.7)

Thus our previous, trivial choices were

(x, t, y, s) = W

· δ(x − y)δ(t − s), etc. (1.5.8)

The notations

•≡



dx, ◦≡



dx, ∗≡



allow us to write J more compactly as

J [u] = f • W

• f + i ◦ W

◦ i + b ∗ W

∗ b + 

w. (1.5.9)

Exercise 1.5.2

Deﬁne the weighted residual or adjoint variable λ(x, t )by

λ ≡ W

•



∂

∂t

+ c

∂

∂x

− F



. (1.5.10)

Then show that the Euler–Lagrange equations for minima of (1.5.9) are just as

before. 

Exercise 1.5.3

Deﬁne C

, the inverse of W

,by

• W

≡



dz C

(x, t, z, r)W

(z, r, y, s) (1.5.11)

= δ(x − y)δ(t − s) . (1.5.12)

Deﬁne C

and C

analogously, and deﬁne C



= I . (1.5.13)

1.5 Regularity of the inverse estimate 29

Each entity in (1.5.13) is an M × M matrix. Now, write out the representer solution

of the Euler–Lagrange equations. Verify that the solution only requires C

, C

and



; that is, it does not require their inverses, the weights W

, W

and w. 

1.5.4

The inverse weights smooth the residuals

The inverse estimate

u obeys

∂

∂t

(x, t) +c

∂

∂x

(x, t) = F (x, t) + (C

• λ)(x, t)

= F(x, t) +



dy C

(x, t, y, s)λ(y, s), (1.5.14)

subject to

u(x, 0) = I (x) + (C

◦ λ)(x, 0), (1.5.15)

and

u(0, t ) = B(t) +c(C

∗ λ)(0, t) . (1.5.16)

The supposition is that C

, C

and C

smooth the singular behavior of λ, yielding

regular estimates for

f ≡ C

• λ,

ı ≡ C

◦ λ and

b = cC

∗ λ, leading in turn to a

regular estimate

u for the ocean circulation.

In summary, we should avoid “diagonal” weighting.

Note 1. The adjoint variables α and λ remain singular, but r and u should become

regular.

Note 2. Evaluation of the convolutions in (1.5.14), (1.5.15) and (1.5.16) at each

position and time is potentially very expensive: consider three space

dimensions and time.

Note 3. Functional analysis sheds much light on smoothness: see §2.6.

Exercise 1.5.4

Consider slow, viscous ﬂow as discussed in Exercises 1.1.3 and 1.2.2. Construct both

the adjoint representers α and the representers r, using the Green’s function φ given in

(1.1.26). How smooth are α and r? Is nondiagonal weighting of either the dynamical

penalty or the initial penalty necessary? 

Exercise 1.5.5

Generalize the deﬁnition of the rk  given in (1.3.30) et seq. Prove that

30 1. Variational assimilation

(i) r

(x, t) = (x, t, x

, t

), (1.5.17)

for 1 ≤ m ≤ M;

(ii)  = γ • C

• γ + γ ◦ C

◦ γ + c

γ ∗ C

∗ γ. (1.5.18)



Note:

The adjoint equations (1.3.1)–(1.3.3) and forward equations (1.5.14)–(1.5.16),

which constitute the most general form of the Euler–Lagrange equations devel-

oped in §1.2 and §1.5, are restated for convenience in §4.2 as (4.2.1)–(4.2.6).

Chapter 2

Interpretation

The calculus of variations uses Green’s functions and representers to express the best

ﬁt to a linear model and data. Mathematical construction of the representers is devious,

and the meaning of the representer solution to the “control problem” of Chapter 1 is not

obvious. There is a geometrical interpretation, in terms of observable and unobservable

degrees of freedom. Unobservability deﬁnes an orthogonality, and the representers span

a ﬁnite-dimensional subspace of the space of all model solutions or “circulations”.

The representers are in fact the observable degrees of freedom.

A statistical interpretation is also available: if the unknown errors in the model

are regarded as random ﬁelds having prescribed means and covariances, then the

representers are related, via the measurement processes, to the covariances of the

circulations. Thus the representer solution to the variational problem is also the optimal

linear interpolation, in time and space, of data from multivariate, inhomogeneous and

nonstationary random ﬁelds. The minimal value of the penalty functional that deﬁnes

the generalized inverse or control problem is a random number. It is the χ

variable, if

the prescribed error means or covariances are correct, and has one degree of freedom

per datum. Measurements need not be pointwise values of the circulation; representers

along with their geometrical and statistical interpretations may be constructed for all

bounded linear measurement functionals.

Analysis of the conditioning of the determination of the representer amplitudes

reveals those degrees of freedom which are the most stable with respect to the observa-

tions. This characterization also indicates the efﬁciency of the observing system – the

fewer unstable degrees of freedom, the better.

Interpreting the variational formulation is completed by demonstrating the relation-

ship between weights, covariances and roughness penalties.

32 2. Interpretation

2.1 Geometrical interpretation

2.1.1 Alternatives to the calculus of variations

After formulating the penalty functional that deﬁnes the best ﬁt to our model and our

data, we found a local extremum using the theory of the calculus of the ﬁrst variation.

Speciﬁcally, we derived the Euler–Lagrange equations, and explicitly expressed their

solution with representers. These functions were deﬁned as special and directly cal-

culable solutions of Euler–Lagrange-like equations. We shall now construct the same

extremum for the penalty functional using Hilbert Space theory (Yoshida, 1980). This

geometrical construction reveals the efﬁciency of minimization algorithms based on

the Euler–Lagrange equations.

Exercise 2.1.1

How do we know that we shall ﬁnd the same extremum? 

2.1.2

Inner products

We begin by deﬁning an inner product for two “ocean circulations” u = u(x, t) and

v = v(x, t ):

u,v≡





∂

∂t

+ c

∂

∂x



u(x, t)



×W

(x, t, y, s)



∂

∂s

+ c

∂

∂y



v(y, s)





dy u(x, 0)W

(x, y)v(y, 0)



ds u(0, t)W

(t, s)v(0, s)

= f

• W

• f

+ u ◦ W

◦ v + u ∗ W

∗ v, (2.1.1)

where f

is the residual for u (Bennett, 1992).

Exercise 2.1.2

Verify that  ,  is an inner product, that is:

(i) u,v=v, u (assume the W are symmetric),

(ii) cu + dw, v=cu,v+dw, v for all real numbers c and d,

(iii) u, u≥0,

(iv) u, u=0 ⇔ u ≡ 0 (nontrivial).

2.1 Geometrical interpretation 33

In terms of the inner product, our penalty functional is

J [u] =u − u

, u − u

+(d − u)

w(d − u). (2.1.2)



2.1.3

Linear functionals and their

representers; unobservables

Consider the linear mapping

u → u(ξ,τ), (2.1.3)

where the lhs is a ﬁeld, while the rhs is a particular value of the ﬁeld. This mapping is

a linear functional: it linearly maps a function to a single number.

Theorem 2.1.1

If the vector space of admissible ﬁelds u, with the inner product  , , is complete (that

is, if it is a Hilbert Space), then there is a function ρ(x, t,ξ,τ) such that

ρ,u=u(ξ,τ). (2.1.4)

So ρ “represents” the measurement process. This is the Riesz representation

theorem. Given ρ, we may express J entirely in terms of inner products (Wahba and

Wendelberger, 1980):

J [u] =u − u

, u − u

+(d −ρ, u)

w(d −ρ, u), (2.1.5)

where ρ

= ρ(x, t, x

, t

), 1 ≤ m ≤ M.

Now, any ﬁeld u = u(x, t) may be expressed as

u(x, t) = u

(x, t) +



m=1

ρ(x, t, x

, t

) + g(x, t), (2.1.6)

where u

is again the solution of (1.2.2)–(1.2.4), and where the ν

are any coefﬁcients,

since we may always choose

g ≡ u − u

− ν

ρ. (2.1.7)

Let us now impose the condition that g is “unobservable”:

ρ

, g=g(x

, t

) = 0 (2.1.8)

for 1 ≤ m ≤ M. That is, g is orthogonal to each ρ

. For a given u and a given u

,we

may use (2.1.8) to derive M equations for the ν

; then g is uniquely deﬁned by (2.1.7).

34 2. Interpretation

2.1.4 Geometric minimization with representers

But we’re not given u; we’re only given u

. Thus ν and g are arbitrary. We wish to

ﬁnd the u that minimizes J [u]. Let us evaluate J using (2.1.5) and (2.1.6):

J [u] =ν

ρ + g, ν

ρ + g

+(d −ρ, u

+ ρ

ν + g)

w(d −ρ, u

+ ρ

ν + g)

= ν

ρ, ρ

ν + ν

ρ, g+g, ρ

ν +g, g

+(d −ρ, u

−ρ, ρ

ν −ρ, g)

w(d −ρ, u

−ρ, ρ

ν −ρ, g).

(2.1.9)

Next impose the M orthogonality conditions (2.1.8), and use the representing property

of ρ to obtain

J [u] = J [ν, g] = ν

ρ, ρ

ν +g, g

+(d − u

−ρ, ρ

ν)

w(d − u

−ρ, ρ

ν). (2.1.10)

The penalty functional J is now expressed explicitly in terms of ν and g. Note that g

only appears once on the rhs of (2.1.10). Clearly J is least with respect to the choice

of g if g, g=0, that is

g =

g ≡ 0. (2.1.11)

We discard the ﬁeld g orthogonal to all the representers. It remains to select the ν

1 ≤ m ≤ M. But ﬁrst note that

≡ρ, ρ



=ρ

,ρ

=ρ

,ρ



= ρ

, t

) = ρ

, t

)

= σ

, (2.1.12)

so σ = σ

and J , which now only depends upon ν, may be expressed as

J [u] = J [ν] = ν

σν + (h − σν)

w(h − σν), (2.1.13)

where h ≡ d − u

. Completing the square,

J [ν] = (ν − ˆν)

S(ν − ˆν) + h

wh − ˆν

S ˆν, (2.1.14)

where S = σ + σwσ and S ˆν = σwh, both of which are given. We ﬁnally minimize J

by choosing ν = ˆν, and then

J ≡ J [ˆν] = h

wh − ˆν

S ˆν. Provided σ is nonsingular,

we may untangle these results to ﬁnd

(σ + w

−1

)ˆν = h, (2.1.15)

which looks familiar.

Recall that our minimizer is

u = u

+ ˆν

ρ +

g, (2.1.16)

where

g satisﬁes (2.1.11), and ˆν satisﬁes (2.1.15).

2.1 Geometrical interpretation 35

2.1.5 Equivalence of variational and geometric

minimization: the data space

Surely the representers ρ deﬁned by the representing property (2.1.4) are the same as

the representer functions r that satisfy the Euler–Lagrange-like system (1.3.8)–(1.3.13),

in which case

σ = R, ˆν =

β ? (2.1.17)

Exercise 2.1.3

Show that

(x, t) = r

(x, t) (2.1.18)

for 0 ≤ x ≤ L,0≤ t ≤ T , and 1 ≤ m ≤ M.

Hint

Consider (2.1.4):

u(x

, t

) ≡ρ

, u

≡





∂

∂t

+ c

∂

∂x



(x, t)



×W

(x, t, y, s)



∂

∂s

+ c

∂

∂y



u(y, s)



dy ρ

(x, 0)W

(x, y)u(y, 0)



ds ρ

(0, t)W

(t, s)u(0, s). (2.1.19)

Integrate the ﬁrst integral by parts, and then compare (2.1.19) to

u(x

, t

) =



dx u(x, t)δ(x − x

)δ(t − t

). (2.1.20)

Since the partially-integrated (2.1.19) must agree with (2.1.20) for all ﬁelds u(x, t)

having initial values u(x, 0) and boundary values u(0, t), we may equate their respective

coefﬁcients, arriving at (1.3.8)–(1.3.13). We have proved that for any ﬁeld u,

r, u=u. (2.1.21)



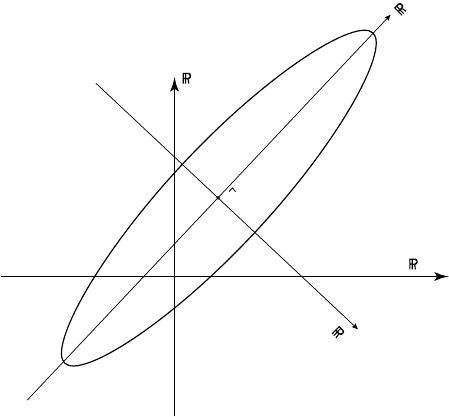
36 2. Interpretation

Note 1. We have established that

u(x, t) − u

(x, t) =

r(x, t). (2.1.22)

That is, the difference between the inverse estimate

u and the prior estimate u

is a linear combination of the M representers r

,...,r

. The difference lies in

the observable space, that is, we reject any additional difference g that is

unobservable: r, g=0. We began with a search for the optimal or best-ﬁt

ﬁeld

u(x, t), where 0 ≤ x ≤ L and 0 ≤ t ≤ T . This would be a search amongst

an inﬁnite number of degrees of freedom (the “state space”). We have exactly

reduced the task to a search for the M optimal representer coefﬁcients

,...,

: see Fig. 2.1.1. These are the observable degrees of freedom (the

“data space”).

Data

State

Figure 2.1.1 The plane represents the state space. It has an

axis u(x, t) for each (x, t) in the intervals 0 ≤ x ≤ L,

0 ≤ t ≤ T . In principle this is an inﬁnite dimensional space.

In practice, when we replace continuous intervals and partial

differential equations with grids and partial difference

equations, the state space usually has a very large but ﬁnite

dimension. The contour is deﬁned by a constant value for the

penalty functional J [u], and has principal axes

Data

(for β

r(x , t )) and R

Null

(for g(x, t)). Note that the

representers r

(x , t ),...,r

(x , t ) are known, and span the

data space, so only the unknown β

,...,β

vary in the data

space. The unobservable ﬁeld g(x , t) is unknown and variable

for 0 ≤ x ≤ L,0≤ t ≤ T . Realizing that

g is zero greatly

reduces the size of the search for

u, as we need only search in

the data space.