Бауэр Ф.Л., Гооз Г. Информатика. Том 1

Подождите немного. Документ загружается.

4.1.

Булева алгебра 281

4.1.3.3.

Отношение порядка

между

булевыми выражениями

Сравнивать

между

собой булевы выражения особенно

удоб-

но

при помощи теоремы 3. Так,

fAg>f,

потому что f Л £-*/ = С1/ V "1 g) Vf = (~\f V /) V 1 g =

L V lg=L

Аналогично

f>fVg.

Далее,

так

как

if Л (/

-+g))->g

= 1 (f А П/ V g)) V g =

((/ Alf) V (f A g)) Vg

Часто из этих отношений можно простым способом вывести

дальнейшие заключения. Допустим, что

/A(/->g)

= |_. Тогда

L > g. Вместе с g>L (теорема 2) это

даёт

g = L. Тем самым

доказана

Теорема

5. Если / Л

(/->§)==

L, то g = L.

Пусть теперь / Л g = L. Тогда в силу соотношений L ^ / Л g

f Ag^f имеем L^=/. Аналогично заключаем, что L^g,

тем самым получена

Теорема

6. Если f /\g = L, то f = L и g=L („неразложи-

мость нейтрального элемента операции .Л." (ср. с

4.1.1.1)).

Далее, из эквивалентности (равнозначности)

двух

имплика-

ций

(субъюнкций)

следует

эквивалентность

двух

отвечающих

им

соотношений порядка Эквивалентны, например, выражения

p-*-(q-*~r) и

(pAq)-*-r,

которые оба можно преобразовать к

~] (р Л q А ~] г). Следовательно, справедлива

Теорема

7. Соотношение p^(q^-r) выполняется

тогда

только

тогда,

когда р Л q^ r.

4.1.3.4.

Приложения к высказываниям и предикатам

Для *# = В

(модель исчисления высказываний) вместо «вы-

сказывание f сильнее, чем высказывание g» говорят также «f

влечёт (за собой) g». Поскольку в этом

случае

f~*~g = U опера-

цию .—>-. тоже называют импликацией. Точно такж

операцию

.-«-*.

называют

эквивалентностью,

так как отношение равенства

есть отношение эквивалентности, я f = g равносильно f

•«-»•

g = i.

В табл. 10 мы понимали . = . как

булеву

операцию; в этом

282 Гл. 4. Двоичные комбинационные и переключательные схемы

разделе соответствующая булева операция

будет

обозначаться

как

.-*->•.,

знак же равенства

будет

использоваться исключитель-

но

как знак отношения (эквивалентности) (причём в речи

обычно рядом фигурирует слово типа „справедливо"). Для

большей ясности

будем

в случае s4- = i писать

ag(A), а стало

быть,

будем

писать,

ag(f-*->f)

в случае эквивалентности f = f

ag(f /\ g-*~f) в случае импликации

f^g^f.

Соотношение

f Ag ^ f читается сейчас так:

(

влечёт 1

высказывание f Л Я J г высказывание f",

(.сильнее, чем ) '

а соотношение f

A(f->g)

>g—как

влечёт )

„высказывание

/ Л(/->£м fвысказывание g",

4 s/

(.сильнее, чем J

По

внешней форме схожи, но доказываются независимо

следующие две теоремы:

Теорема

ag(/Ag)

тогда и только тогда, когда ag(f)

ag(g).

ДОКАЗАТЕЛЬСТВО.

ag(/Ag)

означает,

4TofAg

= i. Значит,

ввиду неразложимости нейтрального элемента, / = i и g = i,

т. е. ag(f) и

ag(g).

Обратно, если ag(f) и ag(g), то / = i и

g = i, а потому f Ag = i, т. е.

ag(/Ag).

Теорема

[modus

ponens

традиционной логики). Если ag(f) и

(

влечёт

• " (^ сильнее, чем

то ag(g).

ДОКАЗАТЕЛЬСТВО.

ПО условию f = i и / > g; значит, i > g

Вместе с g>i (4.1.3.1, теорема 2) это даёт g = i, т. е. ag(g)_

Предикаты возникают, когда строятся высказывания отно-

сительно общих операций, которые приводят к значениям

истинности.

В частности, предикаты выступают в качестве усло-

вий

при разборе случаев. Преобразование предикатов к эквива-

лентному виду и (допустимое) сужение условий-стражей по-

средством перехода к более сильному предикату — это задачи,

с которыми постоянно приходится иметь дело при разработке

программ. Знакомство с аппаратом булевой алгебры позволяет

уверенно решать такие задачи.

Ниже ag — сокращение от

allgemeingiiUig

[общезначимый (нем.).—

Перев.].

Модус понеис, или правило отделения,— самое знаменитое правило

вывода в логике. — Прим. изд. ред.

4.1.

Булева

алгебра

283

Рассмотрим,

например, предикат х ^ 0 в

if х > 0 then х

Q x<0 then -х fi.

По

определению х ^ 0 означает ни больше ни меньше как

V х= 0. Поскольку f > / V g, то х < О сильнее, чем

^ 0, поэтому условие-страж во второй строке можно сузить:

if *>0 then x

•

л; < 0 then — х fi.

Так

как всё ещё JC^OV л; <0 = true, неопределённой ситуа-

ции

возникнуть не может.

Далее, рассмотрим разбор случаев

if х > 1 then if х > 0 then 3 X *

х < 0 then — х fi

Л; < 1

then

x fi.

Предикаты х

~$z

1 и х^О сравнимы; из арифметики (вычисли-

тельная структура Z) мы знаем, что 1 ^ 0, а значит,

Следовательно, если л; ^ 1 = true, то и л; ^ 0 = true (и

< 0 =~] (л: ^ 0) = false). Таким образом, первую из

двух

внутренних ветвей можно освободить от стража, а вторую

вообще отбросить, и мы получаем

if х > 1 then 3 X *

•

х < 1 then Л; fi.

В заключение рассмотрим алгоритм

contains,

который опре-

деляет, содержится ли в данном слове а знак х:

funct

contains

s (string a, charx) bool:

a-<>

then

false

elsffirst(fl)=x

then true

else

con/mns(rest(a),x)

fi .

Его можно преобразовать в „двустрочную" рекурсию:

funct

contains=(string

a, char *) bool :

if a« О V

ftrst{a)**x

then

if <r«О

then

false

д+ О A

first

{a)

then,

true

else

contains

(rest

(a),

x) fi

284 Гл. 4. Двоичные комбинационные и

переключательные

схемы

Можно

ли упростить первую ветвь, когда и как? Интуитивно-

ясно,

что, поскольку стражи

а=<>

Й^ОЛ

first(a)

— х

исключают

друг

друга:

а=<>Л(а¥=ОЛ

first(a)

= x) =

false,

достаточно проверить, выполнено ли условие а — (). Более

формально:

при выполнении условия

а = О V

first(a)

= х

мы имеем а ф О >

first(a)

= x, а значит (см. 4.1.3.1),

по

определению,

(а^ОЛ

first(a)

= х) = (а Ф <».

В результате получаем

/vvs then if a = 0 then false

a+O then true fi

else

дм

Дальнейшее упрощение даёт

funct

contains

(string

char

bool;

a = О V

first

(a)=x

then

else contains (rest

{a),x)

4.7.4.

Таблицы

решений

4.1.4.1.

Совместные таблицы решений

В качестве вспомогательного графического средства пред-

ставления разбора случаев для булевых функций многих пе-

ременных служат так называемые

таблицы

решений.

Пример'

такой таблицы представлен на рис. 141. Каждой переменной

отвечает своя строка, а по столбцам указывается, сама ли пе-

ременная

или её отрицание входит в совершенную конъюнкцию.

Перевод таблицы в

охраняемый

детерминированный' разбор

случаев не составляет проблемы (ниже а, Ь, с, d — вида bool,

Недетерминированные примеры в

литературе

не

встречаются.

4.1.

Булева алгебра

285

и, v, до, х —

вида

int):

со

~](а л

~ib)

со

if я

Ьл СЛ

then и

ал t л с л ~ldthen и

ал

bh~\CK

.о"

then

ал Ь

Л "пс

~~)d

then

Ппал

6 л ел а

then

(*)

D Па л 6 л с л ~id then и

—ia л

—1С

л д

then у

~\а л 6 л

—1с

л па" then и»

Впал~|6л

then и

—ia л —i6 л й л

Па

then

и>

—la л

~\Ь

—(с

о"

then о

Па л

—ift

—1С

л "па

then * fi

Для столбцов, обозначенных „ошибка", ветви

не

предусматри-

ваются;

результат

таком

случае

не

определён. Отсутствие

соответствующих совершенных конъюнкций неизбежно

нашем

примере ввиду зависимости

между

переменными.

Так как „мо-

ложе

14 лет"

влечёт

„до 18 лет

включительно",

то

комбинация

а /\~]Ь, если никаких „сбоев"

нет,

возникнуть

не

может; разбор

случаев „ставится

на

предохранитель" ~\(а

Л~\Ь),

т. е.

а-*-Ь.

Получающаяся упрощенная таблица показана

на рис. 142, при-

чём крестики заменены явным указанием цены билета.

Далее, порядок расположения столбцов

не

имеет значения.

Поэтому столбцы

равными значениями результата можно

У/

моложе 14

лет

до

пет

вкл,

группа

учащиеся

0.50 .марок

1.—марок

1.50

марок

2.— марок

ошибка

R10R11

R12

R13

х-

R14R15

R16

Рис.

141.

Таблица решений

крестиками. [Пример заимствован

из

книги

W. Ebben, Entscheidungstabellentechnik,

Gruyter, Berlin,

1973.

Текстуаль-

но

он

звучит

так:

Пример.

Расценки

на

входные билеты

плавательный бассейн. Дети

моложе

лет—1 марка, подростки

до 18 лет

включительно—1,5 марки,

взрослые

— 2

марки.

Для

групп

не

менее

человек установлен следующий

тариф:

дети

—0,5

марки, подростки—

марка, взрослые—

1,5

марки. Школь-

ники,

студенты

ученики

на

производстве независимо

от

возраста платят

по

детскому тарифу.]

286

Гл. 4.

Двоичные комбинационные

переключательные схемы

R2 R3 R4 R9 RIO RU R12 R13 R14 R15 Rl«

до 14

лет

до

лет вкл,

группа

учащиеся

0.50 0.50 1.- 1.- 0.50 1.- 1.- 1.50 0.50 1.50 I,- ?.-

Рис.

142.

Упрощённая таблица решений.

до

лет

до

лет вкл.

Группа

учащиеся

R1 R2

R9 R13 R3

О.5О

RIO R11

1,-

R15

R12 R14

1.50

R16

2,-

Рис.

143.

Таблица решений

объединенными

по

результатам столбцами.

объединить (рис. 143). Этому отвечает дизъюнкция (дизъюнк-

тивное объединение) соответствующих совершенных конъюнкций:

( я л Ь\ с к d)v (ал fc л ел

—id)

(~ia

л Ал ел d)

v(—\ал~ibл

ел d)

then

0 ( ел

Ъ\—[ск

d)v (ал

ЙЛ-|СЛ-1</)У(-1ЛЛ

£л

CK~\d)

у(-юл

£л-мл

«0 v (~>

л "1* л -1С л <0

then

0(~1йА 4л~1СЛ-1<0

V(~WA~ifcA

(

*ПЛЛ-1&АТ1СЛ-1</

then

thenx

В качестве стражей стоят четыре высказывания в дизъюнктив-

ной

нормальной форме. Закон дистрибутивности позволяет

упростить это, например, до

сл(ал*у-!аЛ(() then

-ic л

(а лЬ

V-ia л

d\v-\a hbКС

A~\dthen

—\a

—\d

л (6

-тс

—ib

с)

then

—ia

—id

л (—\b

—ic) then

x fi

таблицами решений так далеко уйти нельзя, и уже одно это

показывает границы их применения. Единственный способ упро-

стить таблицу — это объединить столбцы, если

результат

не зави-

4.1.

Булева

алгебра

287

сит от одной (или нескольких) переменных; соответствующие

„пустые места" отмечаются в таблице прочерком (рис. 144).

до 14 лет

до 18 лет вкл.

группа

учащиеся

R1/2

—

0.50

R9/13

—

0.50

R3/4

—

R10

1 __

R11/15

1.—

R12

1.50

R14

1.50

R16

2,-

Рис. 144. Таблица решений с прочерками.

Зависимость между переменными позволяет сократить число

„задаваемых вопросов"; в нашем примере ввиду импликации

до

14 лет

до

Шлет

вкл.

группа

учащиеся

R1/2

—

0.50

R9/13

0.50

R3/4

—

1,—

R10

1,—

RI1/15

—

1—

R12

1.50

R14

1.50

R16

2.-

Рис. 145. Таблица решений с

предохранителем

а->-Ь.

-*•

b можно отказаться от b в R1/2 и R3/4, а ввиду

-+~\

а —

от а в R14 и R16 (рис. 145). Получается охраняемый разбор

случаев

со а-+Ь со if а л с then и

О ~\а л ел d then и

Da л —ic then v

-la л Ь л ел

—\d

then о

D —\а л —ic л d then v

—\a A ft л —ic л —\d then n>

D —* л с л ~ut then w

0 —ф A —ic л

-irfthen

x fi

с восемью, но всё-таки не с четырьмя ветвями.

4.1.4.2.

Последовательные

таблицы решений

Таблицы решений используются обычно не описанным выше

„совместным"

способом, а последовательным способом, осу-

ществляя проверку условий слева направо. Поэтому объедине-

288

Гл. 4.

Двоичные комбинационные

переключательные схемы

ние

произвольных столбцов теперь не разрешается — всё за-

висит от порядка рассмотрения столбцов. Такие таблицы ре-

шений

соответствуют

последовательному

разбору случаев.

Rl/2 R3/4 R9/I3 R10

последовательная

Rll/15

R12 RI4 Rie

до 14 лет

до

лет вкл.

группа

учащиеся

Т Т

—. —

т —

0.50 1,—

•»

0.50

—

1.50

—

1.50

—

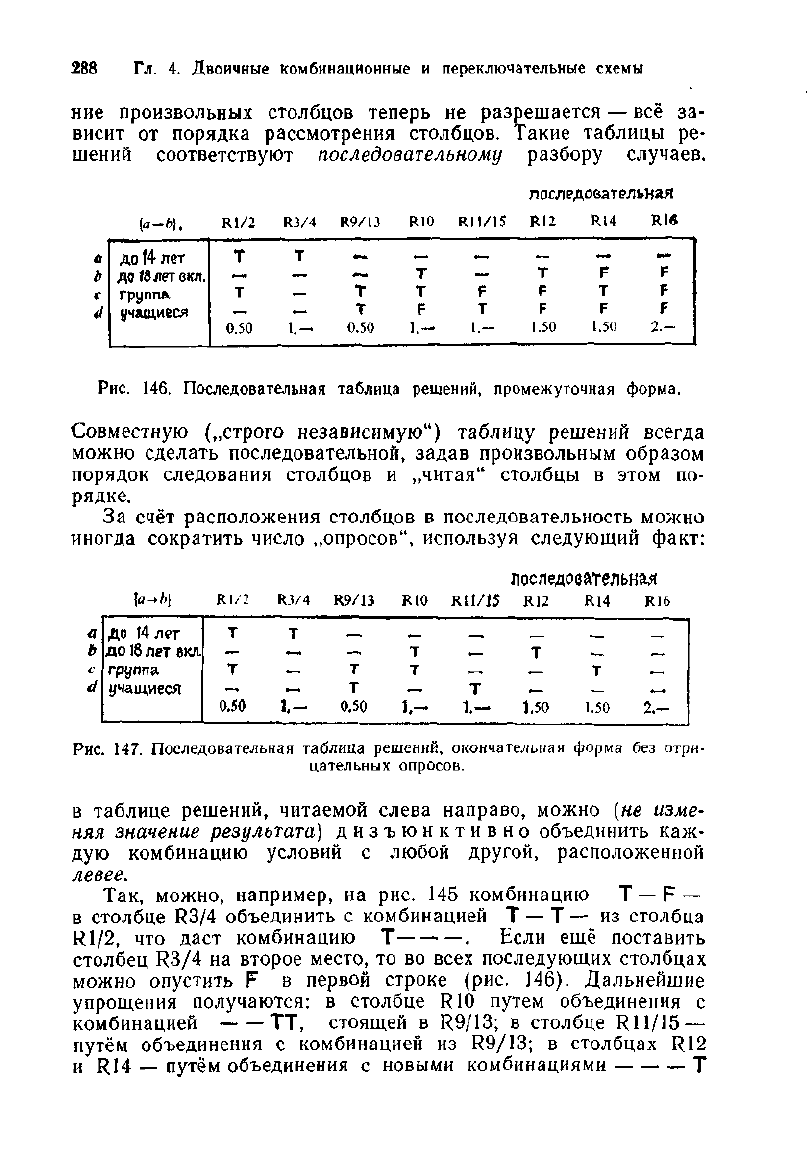
Рис.

146.

Последовательная таблица решений, промежуточная форма.

Совместную („строго независимую") таблицу решений всегда

можно сделать последовательной, задав произвольным образом

порядок

следования столбцов и „читая" столбцы в этом по-

рядке.

За

счёт расположения столбцов в последовательность можно

иногда сократить число „опросов", используя следующий факт:

последовательная

(fl->/>) Rl/2 R3/4 R9/13 R10

Rll/15

R12 RU R16

Рис.

147.

Последовательная

таблица

решений, окончательная форма

без

отри-

цательных опросов.

таблице решений, читаемой слева направо, можно

{не

изме-

няя

значение

результата)

дизъюнктивно объединить

каж-

дую комбинацию условий

любой другой, расположенной

левее.

Так,

можно, например, на рис. 145 комбинацию Т—F —

столбце R3/4 объединить с комбинацией Т — Т — из столбца

R1/2, что

даст

комбинацию Т . Если ещё поставить

столбец R3/4 на второе место, то во

всех

последующих столбцах

можно опустить F в первой строке (рис. 146). Дальнейшие

упрощения получаются: в столбце R10 путем объединения с

комбинацией

ТТ, стоящей в R9/13; в столбце

R11/15

—

путём объединения с комбинацией из R9/13; в столбцах R12

R14 — путём объединения с новыми комбинациями Т

До

лет

до 18

лет

вкл.

группа

учащиеся

—

—.

0,50

—

1—

—

0.50

1,—

1.—

1,50

— —.

1.50 2,—

4.1.

Булева

алгебра

289

из

R11/15

—ТТ—

из R10.

Наконец, таким

же

способом

устраняются

все F в

столбце

R16. В

результате получаем

таб-

лицу

(рис. 147), в

которой „отрицательных опросов"

нет.

Всё-таки

получающемся последовательном разборе

случаев

со

a-tb СО if а АС

then

elsf

a then г

elsf

Arfthen

elsf

А с then v

elsf

d thenj;

elsf

b then vr

elsf

с then w

else

x ft

глубины

остаётся

ещё 10

опросов. Таблицы решений

как

инструмент

для

упрощения разбора случаев оптимальны

не во

всех отношениях.

Из

приведенной формы

(*)

можно, например,

получить древовидный разбор случаев

if a Kb

Ч—\а Л

d then if с tnen «

else

v fi

elsf

С then v

elsf

—\b

"ic then x

else

w fi

с всего

опросами

глубины

3. А из

исходной таблицы считы-

вается разбор случаев

if -id then

else

—if then

else

—IC

then

else

elsf

then

else

then

elsf

then

else

fi fi

с всего

опросами

глубины

4 —

вариант, особенно выгодный

случае, если цены билетов

будут

часто изменяться.

4.1.5.

Переключательные

функции

В этом разделе (двоичные) переключательные функции,

т. е.

булевы функции

над

моделью

BIT (см.

4.1.1.5),

исследуются

точки зрения

их

технической реализации.

•Jx

290

Гл. 4.

Двоичные комбинационные

переключательные

схемы

4.1.5.1.

Символические изображения переключательных функций

Реализацию переключательной функции

f от п

переменных

представляют себе

как

„чёрный ящик"

F с

входами

, ...

...,

выходом 1(а\,

, ..., а

При

этом совсем

не

обязательно-

ограничиваться одним выходом;

в-

общем случае имеется

переключа-

тельных функций

ji =

fi(a

•••

,. , а

), i = 1, 2, . . ., т, для

выхо-

дов

/i \

(рис. 148).

Такое

„функциональное

образование",

на-

зываемое

комбинационной

схемой

(для

т =

—

переключательным

элементом),

можно рассматривать

как

кодовый преобразователь („пе-

рекодировщик")

п-разрядными

двоичными словами

на

входе

m-разрядными двоичными

сло-

вами

на

выходе.

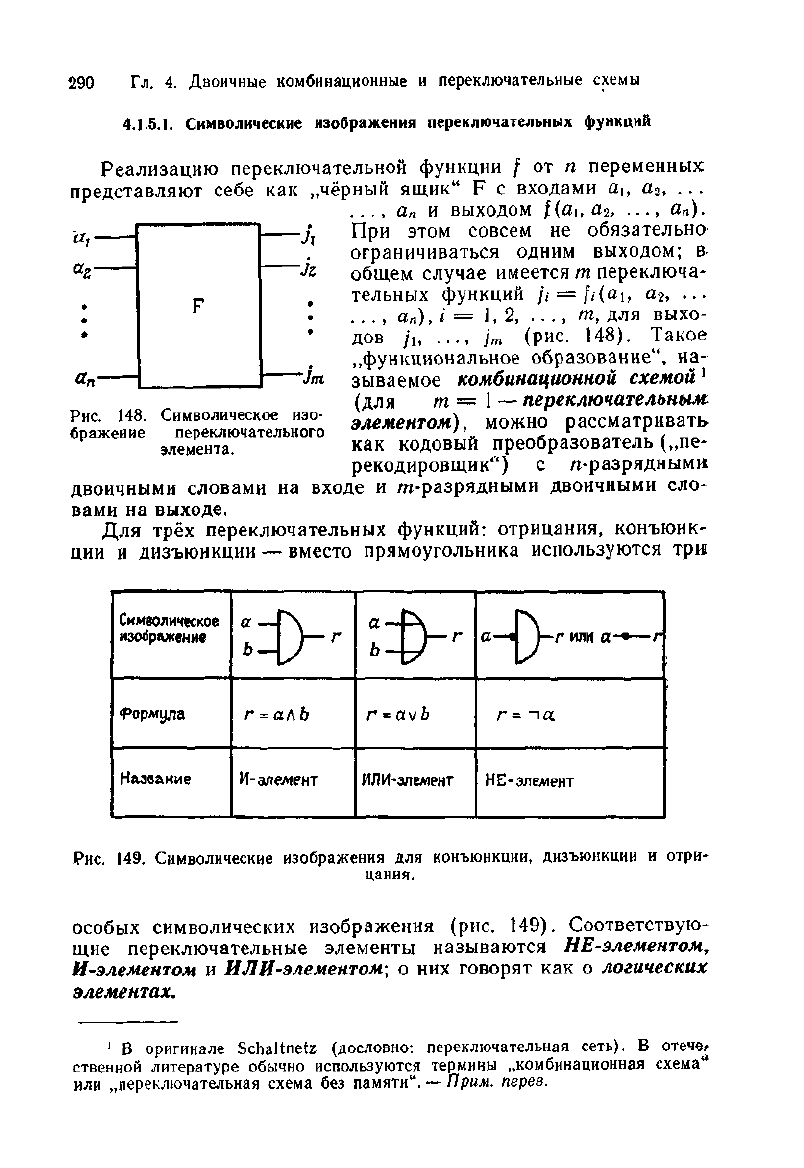
Для трёх переключательных функций: отрицания, конъюнк-

ции

дизъюнкции

—

вместо прямоугольника используются

три

Рис.

148.

Символическое

изо-

бражение

переключательного

элемента.

Символическое

изображение

Формула

Название

= алЬ

И-апемент

ИЛИ-алемент

а—4

j~r

или

а-«—г

~<а

НЕ-элемент

Рис.

149.

Символические изображения

для

конъюнкции, дизъюнкции

отри-

цания.

особых символических изображения

(рис. 149).

Соответствую-

щие переключательные элементы называются

НЕ-элементом

И-элементом

ИЛИ-элементом;

о них говорят как о

логических

элементах.

оригинале Schaltnetz (дословно:

переключательная

сеть).

отече?

ственной

литературе

обычно

используются

термины „комбинационная

схема"

или „переключательная

схема

без

памяти".

—

Прим.

перев.