Бауэр Ф.Л., Гооз Г. Информатика. Том 1

Подождите немного. Документ загружается.

/1Г

7(2)

get!®

ТП П

>«n«

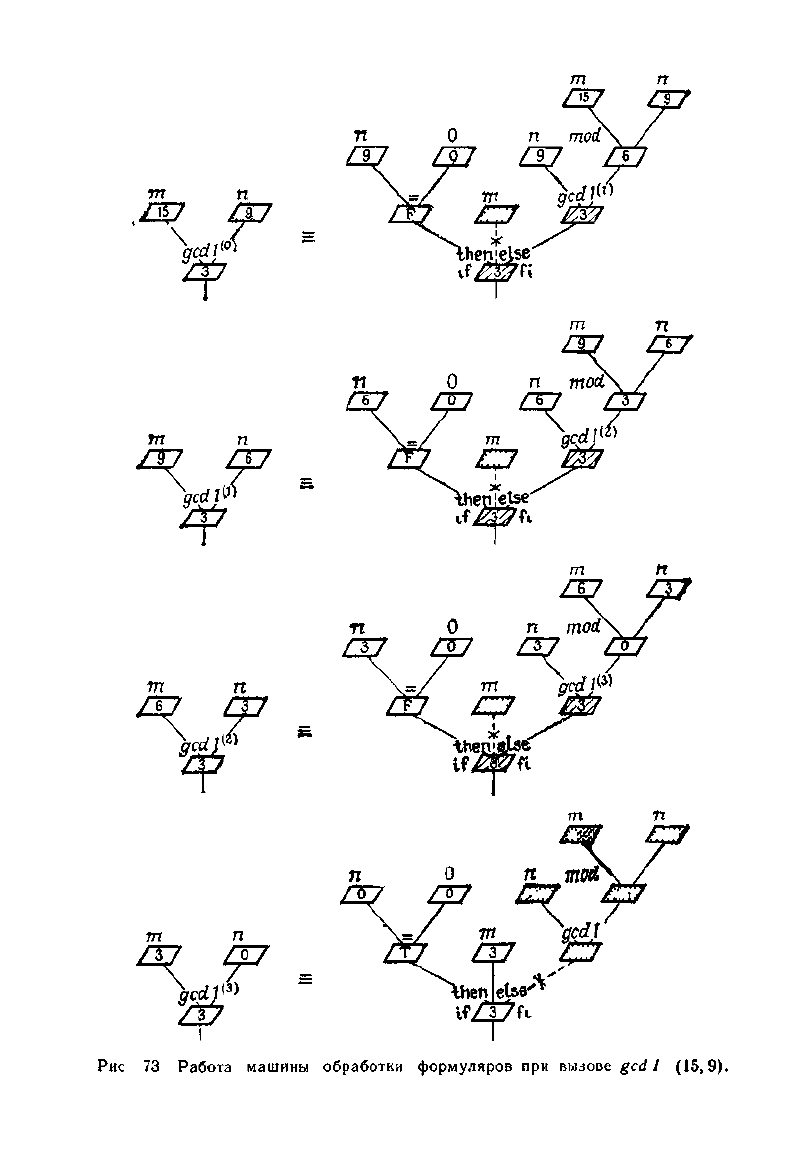
Рис

73 Работа машины обработки формуляров при вызове gcd 1 (15,9).

142

Гл.

Основные понятия программирования

sort

•sort

sort

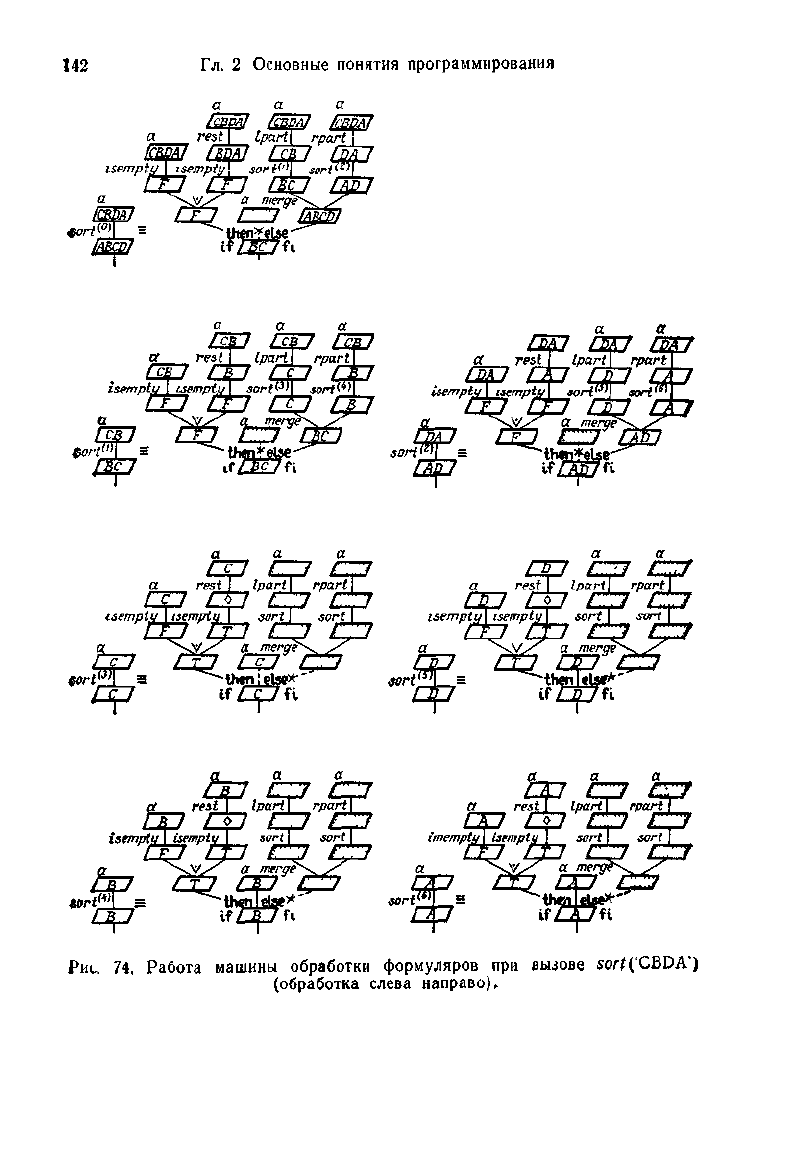
Рис.

74,

Работа машины обработки формуляров

при

вызове

sort

('CBDA')

(обработка слева направо).

2.3.

Подпрограммы

143

В случае иерархических вызовов, как например в приводи-

мой

ниже подпрограмме

modi

(„быстром" варианте подпро-

modl(Ul,

19)

modi

(modi

(П1,Щ,

19)

modi

(modi (modi (W,16),3%), 19)

modi

(modi (modi (61,76), 38), 19)

modi

(modi (61,38), 19)

modi

(modi (23,38), 19)

mod 1(23,19)

modi

(4,19)

Рис.

75. Вычислительный формуляр Рис. 76. Ход вычислений при вызове

принцип магазина.

modi

(137, 19).

граммы mod из

2.3.2)

для вычисления остатка при целочислен-

ном

делении, это означает обработку „изнутри наружу";

funct

modis(\nt

njjint

со/и=50лл>0

со) int:

if m S 2 x л

then

modi

(modi

(m, 2 x и), n)

elsf

m 5«

then

mo</7

(jn—n,

else

/»z fi.

В совместных ситуациях всё ещё сохраняется свобода вычисле-

ний.

В конкретных версиях машины обработки формуляров от

неё часто отказываются. Если, скажем, дополнительно потребо-

вать, чтобы в случае совместности обработка производилась

последовательно „слева направо", то мы получаем

„принцип

магазина"

Бауэра и Замельзона (1957 г.)

для последователь-

ного вычислительного процесса:

ходе

вычисления

считываемые

слева

направо

операции

(как

примитивные,

так и

описанные)

откладываются,

если

их

аргументы

еще не

(полностью)

подготовлены,

выполняются,

как

только

их

аргументы

полностью

подготовлены,—

„отклады-

ваются по

необходимости,

наполняются

по

возможности".

В оригинале „Kellerprinzip" (Keller — погреб, подвал). Имеется в виду

магазин винтовки (патрон, помещённый

туда

последним, выстреливается

первым).

См. также

3.7.2.—

Прим. изд. ред.

Патенты за номерами

3047228

(США) и

1094019

(ФРГ).

Это правило обработки эквивалентно leftmost-innermost computation

rule [правилу лево-внутреннего вычисления; см.

8.2.6.

— Изд. ред.] Морриса

(1968 г.).

144

Гл. 2. Основные понятия программирования

Получаемый таким образом порядок выполнения формулы

(*) из 2.2.2 показан на рис. 75. Процесс вычисления при вызо-

ве

modi

(137, 19) представлен на рис. 76.

Проведённые ранее рассмотрения без

труда

переносятся на

системы (рекурсивных) подпрограмм, например на систему

(iseven,

isodd)

из

2.3.2,

в которой мы имеем дело с косвеннной

рекурсией. Для рекурсивных систем вроде

(gcdl,

mod) речь

идёт, очевидно, о рекурсии внутри рекурсии.

Об особой роли частного случая повторительной рекурсии

мы ещё поговорим в гл. 3.

2.4. О

технике

рекурсивного

программирования

2.4.1 *. Как

приходят

рекурсивным

подпрограммам?

Нет

готовых рецептов, как для данной произвольной пробле-

мы получить (рекурсивный) алгоритм её решения. Однако не-

которые рекомендации имеются.

2.4.1.1.

Органически

рекурсивные

определения

Многие

рекурсивные подпрограммы являются точным „слеп-

ком"

с соответствующего определения. Это верно, скажем, в от-

ношении

подпрограммы fac. Иначе обстоит дело с классическим

определением возведения в степень. Оно попадает под общую

схему

я-кратно итерированной операции р, где .р. — любая вну-

тренняя

двуместная ассоциативная операция над произвольным

сортом X, соотв. X (область значений параметра п ограничивает-

ся

положительными натуральными числами):

funct

iter^Q-a,

int n

со и > 0 со) X:

if « = 1

then

else

ар

iter(a,

n— 1) fi

function

Her

{a : А; Я:

integer

begin

if n = 1

then

Her -к а

else

tier

cap

iter(a,

n — l)

end

2.4.1.2.

Извлечение

рекурсии

из

постановки

задачи

В большинстве случаев, однако, рассматриваемая задача

не

является алгоритмически сформулированной. Поэтому пы-

таются прийти к (рекурсивному) алгоритму, сводя общую за-

дачу

к „более простым" задачам того же рода, см 1.6.3 и

2.3.2.

* Этот раздел можно пропустить,

2.4.

технике

рекурсивного программирования

145

Точнее говоря, речь идёт

получении достаточного числа

(ус-

ловных) уравнений, определяющих искомую функцию.

Иногда

непосредственно

ясно,

как это

сделать,

но

чаще

всего требуется интуиция. Например,

для

решения задачи

на-

хождения наибольшего общего делителя

двух

(положитель-

ных) чисел можно привлечь следующий математический

ре-

зультат:

если

а —

большее

из

двух

чисел

а и Ь, то

пары

а, Ь

а — b, b

имеют одни

и те же

делители,

значит, один

и тот

же наибольший общий делитель. Отсюда непосредственно

сле-

дует

алгоритм

gcd из 2.3.2

(Ь).

Оправдывая одно замечание, сделанное

2.1.3.1, покажем

здесь также,

как

можно определить сложение цгяых чисел,

опираясь

на

операции перехода

следующему

предыдущему

числам.

При

этом одновременно

будет

отсвачено

вычитание,

ибо прибавление отрицательного числа есть вычитание соот-

ветствующего положительного.

силу законов ассоциативности

коммутативности имеем

{а + 1) +

(Ь—

1)= а+ Ь.

Поэтому операцию сложения можно

ввести

так:

funct

plus

(Int

int :

then

plus

1,6-1)

then

plus

-1,

function

plus

[a,

integer):

integer

{

begin

then

plus

« a

/>>0

then

,p/i«

plus(SIICC(a),

predip))

then

plus

plus(pred(a),

succ(b))

end

F-Сли

ограничиться сложением натуральных чисел,

то

третья

ветвь отпадает.

2.4.1-3.

Вложение

Если

не

удаётся

извлечь рекурсию

из

самой постановки

задачи,

то

часто оказывается полезным обобщить

задачу

(на-

пример,

введя дополнительные параметры); подходящее обоб-

щение

позволяет усмотреть возможность рекурсии,

возвра-

щаясь

частному случаю,

мы

получаем алгоритм

для

первона-

чальной задачи.

Классический

пример применения такого приёма

вложения

дал Маккарти

в 1962 г.

Исходная задача была

isprim(n):

«Установи, является

ли

заданное положительное

натуральное число

простым.»

Ниже

рпт —от

prime

number (простое число).

—

Прим.

изб. ред.

146 Гл.

Основные понятия программирования

При

этом предполагается, что известно определение простого

числа:

«Натуральное число п называется простым, если оно боль-

ше 1 и не делится ни на одно число, большее или равное 2

меньшее п.»

Удачным обобщением

будет

такая задача (в которой вводится'

один

дополнительный параметр):

ispr(n,

m): «Установи, верно ли, что заданное натураль-

ное

число п не делится ни на одно число, большее или рав-

ное

т и меньшее п.»

(Не

уменьшая общности, можно считать, что 2 ^ т ^ п.)

Но

для этой новой задачи

ясно,

что

ispr(n,

m) истинно, во-

первых, если т = п, и, во-вторых, если истинно

ispr(n,

m-\- 1)

л не делится на т, и мы приходим к подпрограмме

unct

ispr&

(int

it,

со 2йш</1

со)

boot:

if m^n

then

true

else

(// mod

ш + 0)

function

ispr(n,

integer

{2£тйп))\

Boolean

begin

lfm-я

then

ispr

-е

true

else

ispr<i(n

mod

m+0)

and

end

В этой подпрограмме содержится еще заключительное „захло-

пывание"

всех

„задержанных"конъюнкций. От него можно из-

бавиться и обеспечить за счёт этого более раннее окончание,,

заменив

конъюнкцию на альтернативу

(2.2.3.4)

и перейдя тем

самым к повторительной рекурсии:

funct

isprte

(int it, m

со

СО)

boolj

;и=я

then

true

else

if n mod m

then

false

else

ispr(ti,m

l) fi fi

function

ispr()t,m:

integer

\2<тйп})'.

Boolean

begin

if m

—

then

ispr

true

else

if n mod m

then

ispr

-t:

false

else

ispr

-p

ispr(jt,

end

2.4.

технике рекурсивного программирования

147

В качестве частного случая получаем интересующую

нас под-

программу:

funct

isprim

(fnt

со

ritk

1 со)

bool:

if/i=l

then false

else

ispr(n,2)

function

Isprim

(n:

Integer

[п^Ц):

Boolean;

begin

if n

then

isprim

-z-fahe

else

isprim

ispr(n,2)

end

Впрочем, подпрограмму

ispr

можно

ещё

усовершенствовать,

за-

менив

условие

т = п на т f 2 > п. Эту

подпрограмму обозна-

чим

ispr'.

Если верно

ispr' (n, 2), то у л нет

делителя

удов-

летворяющего условию

2 ^ t < т, где т —

наименьшее число,

funct/дс

(int

со п

со)

int:

facr{U

и)

f unct/«crs (int у,

со

niO

со)

int:

ifn-0

then

function

fac(n

integer

[nfe

0});

integer',

begin

fac^facr(l,n)

end

function

facriy,

integer

{n£,0}):

integer;

begin

if n = 0

then/atr

«y

else/аст

<=facr(y*n,

—

end

Рис.

77.

для которого

n,—

противном случае

мы

имели

бы

окон-

чание

выдачей

false.

Далее, если

бы у я был

делитель

t\,

^ U < я, то был бы и

делитель

, 1 < /2 < m.

Следователь-

но,

у п нет

делителя

/, 2 ^ / < «.

помощью вложения иногда удаётся

для уже

имеющейся

рекурсии получить повторительную редакцию. Если

определить двуместную функцию

facr

как

facr(y,

п) — у X

X fac(п),

т. е.,

грубо говоря

(при п > 0), как у X

— ОХ

X(п

—

2JX---X2X1,

то,

ввиду ассоциативности умножения,

для

п > 0

facr(y,п)

= facr{y X п,п — 1),

facr(y,0)

= y,

мы

приходим

повторительной системе, представленной

на

рис.

77.

Ниже

г (в /асг) — от

repetitive

(повторительный).

—

Прим.

изд. ред.

148 " Гл. 2.

Основные

понятия

программирования

2.4.1.4.

Метод

родственных

задач

Как,

однако, прийти к паре

(iseven,

isodd)

рекурсивных под-

программ из

2.3.2?

Вместо того чтобы вкладывать

задачу

в бо-

лее общую, при использовании

метода

родственных

задач

к ней

„приставляют" одну или несколько задач таким образом, чтобы

подпрограммы из возникающей системы опирались

друг

на

друга.

Прежде всего

задачу

(с) из 2.3.2 можно сформулировать

словами так:

iseven

(m): «Установи, содержит ли данная последователь-

ность знаков m чётное число знаков.»

При

этом справедливо очевидное утверждение:

«Число знаков в последовательности четно

тогда

и толь-

ко

тогда,

когда все знаки

могут

быть сгруппированы в

пары.»

Если

теперь ввести родственную

задачу

isodd(m): «Установи, содержит ли данная последователь-

ность знаков m нечётное число знаков.»,

то обнаруживается взаимосвязь

двух

задач: непустая последо-

вательность знаков содержит нечётное число знаков в том и

только том случае, если после удаления одного знака она со-

держит чётное число знаков,— и чётное, если после удаления

одного знака остаётся нечётное число знаков. Далее, пустая

последовательность знаков тоже может сгруппироваться в

(пустое) множество пар и, следовательно, содержит чётное,

а стало быть, не нечётное, число пар. Мы приходим к таким

формулировкам:

iseven(m):

«Если последовательность m пуста, то: да.

В противном случае: Установи, содержит ли укороченная на

один

знак последовательность нечётное число знаков.»

isodd(m): «Если последовательность m пуста, то: нет.

В противном случае: Установи, содержит ли укороченная

на

один знак последовательность чётное число знаков.»

Из

этих словесных формулировок вытекают основанные на ба-

зовой операции

rest

из

2.1.3.4

формулировки, данные в 2.3.2(с).

Рассмотрим

сходную

задачу

ispos(m):

«Установи, четно ли число минусов в заданной

последовательности m знаков плюс и минус».

Ниже

pos—

от

positive

(положительный), neg — от

negative

(отрица-

тельный).

—

Прим.

изд. ред.

2.4. О технике рекурсивного программирования

149

Она

возникает при определении знака произведения по знакам

отдельных множителей. Разумеется, имеет значение лишь число

net

isposз(string m) boot!

m =

then

true

elseif/ir.sf(m)*»"~"

then

isneg

(rest

(m))

Ofirst(m)~"+"

then

ispos

(rest

(m))

fi fi

net

isneg

(string

m) boo!:

m =

then

false

else

Jirst(m)

"~"

then

ispos

(rest

(m))

UJirst(m)=>"+"

then

/snt'9

(rest(m))

fi fi

Рис.

function

ispos

(m :

string):

Boolean;

begin

jf isempty(m)

then

ispos

»гме

else if_/iw<(m) = '—'

then

ispos

w«e<7 (re.v( (m))

D./ir5<(m)=4-'

then

ii/)Oi

ispos

(rest

(m))

end

function

isneg

(m:

string):

Boolean

;

begin

if isempty(m)

then

isneg

-c

false

else

first

(m) = '~

'•

then

w»egr

-s

ispos

(rest

(m))

[lfirst(m)

= '+'

then

lines'«isneg

(rest

(m)}

end

78.

знаков

минус. Поэтому мы приходим к следующей формули-

ровке:

ispos(т):

«Если последовательность т пуста, то ответ —

„да".

В противном случае, если на первом месте стоит

знак

минус: Установи, содержит ли укороченная на пер-

вый

знак последовательность нечётное число минусов; если

же нет, то: Установи, содержит ли укороченный на первый

знак

ряд чётное число минусов.»

аналогично для функции

isneg.

В результате получается

система подпрограмм, представленная на рис. 78. Здесь

уже нельзя исключить одну из подпрограмм путём подста-

новки;

речь идёт о паре с (неустранимо)

перекрёстной

рекур-

сией.

2.4.1.5.

Использование

характеристических свойств

Часто бывает полезно сначала выявить какие-нибудь харак-

теристические свойства поставленной задачи. Например, для

150

Гл. 2.

Основные понятия программирования

задачи

о том,

является

ли а

полсловом слова

b (см.

1.6.2(g)),

характеристическим предикатом может служить

«Существуют

последовательности

и, и,

такие

что и + а +

v = b.»

Разбирая

отдельно случаи, когда последовательность

пуста

когда

она

непуста, приходим

рекурсивному алгоритму,

опи-

рающемуся

на

вспомогательную

задачу

«Установи, является

ли

последовательность

началом

по-

следовательности

Ь.»

Иногда

бывает целесообразно переформулировать характе-

ристическое

свойство задачи

так,

чтобы

из

него можно было

извлечь какой-либо (другой) алгоритм.

Так,

задаче:

для

заданного натурального числа

п ^ 1

определить (единственное) натуральное число

Ш(п),

такое

что

-i

<;^ <

необходимо выполнение предиката Р(Ш(п),п),

где Р

задаётся

•следующим образом:

Р(а,

«) =

~'<гс<2

Но

для

этого характеристического предиката

Р(а, п)

имеет

место очевидная рекурсия

(

а = 1 при п — 1,

Р{а

п)==

{

P(a-l,n

div 2) при п>\,

значит,

ld(n) допускает рекурсивное определение

{

при я=1,

/d(ndlv2)+l

при п>\,

из

которого получаем алгоритм:

funct

Ids (int n со л й

со) int:

then

e!seW(wd!v2)

+ l

function

ld(n : integerlfit, 1}):

integer;

begin

« =

then Id

else Id о

Qidlv

end

Обычно

характеристические свойства определяют алгоритм

не

однозначно.

Это

особенно ярко видно

на

примере задачи

Ниже

Id — от

латинского logarithmus

dualis

(двоичный логарифм).—

Прим.

изд. ред.