Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

100 2. Nuclear models and stability

Highly excited states that can emit neutrons appear is resonances in the

cross-section of low-energy neutrons. Examples are shown in Fig. 3.26 for

states of

236

Uand

239

U that decay by neutron emission to

235

Uand

238

These states are also important in the operation of nuclear reactors.

2.8 The production of super-heavy elements

One of the most well-known results of research in nuclear physics has been

the production of “trans-uranium” elements that were not previously present

on Earth. The ﬁrst trans-uranium elements, neptunium and plutonium, were

produced by neutron capture

238

U →

239

U γ , (2.63)

followed by the β-decays

239

U →

239

Np e

−

1/2

=23.45 m (2.64)

239

Np →

239

Pu e

−

1/2

=2.3565 day . (2.65)

The half-life of

239

Pu is suﬃciently long, 2.4 × 10

yr, that it can be studied

as a chemical element.

Further neutron captures on

239

Pu produce heavier elements. This is the

source of trans-uranium radioactive wastes in nuclear reactors. As shown in

Fig. 6.12, this process cannot produce nuclei heavier than

258

100

Fm which decays

suﬃciently rapidly (t

1/2

=0.3 ms) that it does not have time to absorb a

neutron.

Elements with Z>100 can only be produced in heavy-ion collisions. Most

have been produced by bombardment of a heavy element with a medium-A

nucleus. Figure 2.19 shows how

260

Db (element 104) was positively identiﬁed

via the reaction

249

Cf →

260

Db + 4n . (2.66)

Neutrons are generally present in the ﬁnal state since the initially produced

compound nucleus, in this case

264

Db, generally emits (evaporates) neutrons

until reaching a bound nucleus. Such reactions are called fusion-evaporation

reactions.

The heaviest element produced so far is the unnamed element 116, pro-

duced as in Fig. 2.20 via the reaction [29]

248

Cm →

296

116 . (2.67)

Abeamof

Ca is used because its large neutron excess facilitates the pro-

duction of neutron-rich heavy nuclei.

As shown in the ﬁgure, a beam of

Planned radioactive beams (Fig. 5.5) using neutron-rich ﬁssion products will

increase the number of possible reactions, though at lower beam intensity.

Exercises for Chapter 2 101

ions of kinetic energy 240 MeV impinges on a target of CmO

. At this energy,

the

296

116 is produced in a very excited state that decays in ∼ 10

−21

sby

neutron emission

296

116 →

292

116 4n . (2.68)

The target is suﬃciently thin that the

292

116 emerges from the target with

most of its energy.

Only about 1 in 10

collisions result in the production of element 116,

most inelastic collisions resulting in the ﬁssion of the target and beam nuclei.

It is therefore necessary to place beyond the target a series of magnetic and

electrostatic ﬁlters so that only rare super-heavy elements reach a silicon-

detector array downstream.

The

292

116 ions then stop in the silicon-detector array where they even-

tually decay. The three sequences of events shown in Fig. 2.20 have been

observed. The three sequences are believed to be due to the same nuclide

because of the equality, within experimental errors, of the Q

. The lifetimes

for each step are also of the same order-of magnitude so the half-lives can

be estimated. The use of (2.61) then allows one to deduce the (A, Z)ofthe

nuclei, conﬁrming the identity of element 116.

Eﬀorts to produce of super-heavy elements are being vigorously pursued.

They are in part inspired by the prediction of some shell models to have an

island of highly-bound nuclei around N ∼ 184, Z ∼ 120. There are spec-

ulations that elements in this region may be suﬃciently long-lived to have

practical applications.

2.9 Bibliography

1. Nuclear Structure A. Bohr and B. Mottelson, Benjamin, New York, 1969.

2. Structure of the Nucleus M.A. Preston and R.K. Bhaduri, Addison-

Wesley, 1975.

3. Nuclear Physics S.M. Wong, John Wiley, New York, 1998.

4. Theoretical Nuclear Physics A. de Shalit and H. Feshbach, Wiley, New

York, 1974.

5. Introduction to Nuclear Physics : Harald Enge, Addison-Wesley (1966).

Exercises

2.1 Use the semi-empirical mass formula to calculate the energy of α particles

emitted by

235

. Compare this with the experimental value, 4.52 MeV. Note

that while an α-particles are unbound in

235

U individual nucleons are bound.

Calculate the energy required to remove a proton or a neutron from

235

102 2. Nuclear models and stability

α emitters

decay time

20 30 keV

8.2

8.4

8.6 MeV

10 20 30

40 s

8.5

8.0 9.0 MeV

3 s

beam

mylar tapenozzle

Ge diode (x−ray)

He jet

256

258

257

260

=1.52 s

1/2

100

decay time

distribution

260

spectrum of

256

258

1/2

=23.6 s

spectrum of

produced in

249

collisions

α emitters

following

260

Db decay

distribution

256

of Lr

x−rays

conincident

260

Dbwith

decay

Expected for

256

(α)Si diode

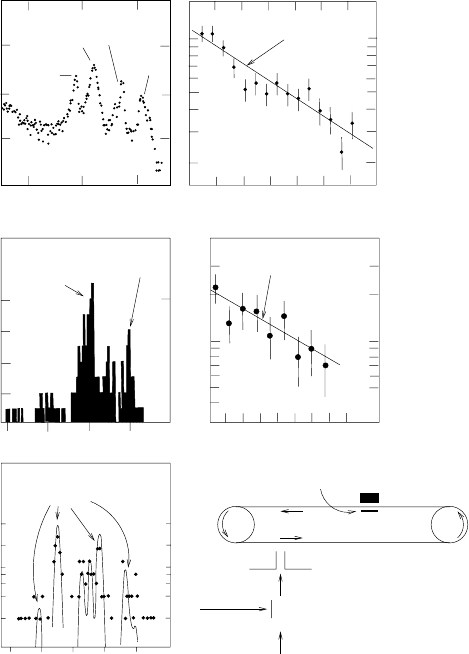
Fig. 2.19. The production and identiﬁcation of element 105

260

Db via the reaction

249

Cf(

N, 4n)

260

Db [28]. As shown schematically on the bottom right, a beam

of 85 MeV

N nuclei (Oak Ridge Isochronous Cyclotron) is incident on a thin

(635 µgcm

−2

) target of

249

Cf (Cf

) deposited on a beryllium foil (2.35 mg cm

−2

Nuclei emerging from the target are swept by a helium jet through a nozzle where

they are deposited on a mylar tape. After a deposition period of ∼ 1s, the tape

is moved so that the deposited nuclei are placed between two counters, a silicon

diode to count α-particles and a germanium diode to count x-rays. The α-spectrum

(upper left) shows three previously well-studied nuclides as well has that of

260

at ∼ 9.1 MeV. The top right panel shows the distribution of decay times indicating

1/2

=1.52±0.13s. Conﬁrmation of the identity of

260

Db comes from the α-spectrum

for decays following the the 9.1 MeV α-decays. The energy spectrum indicates that

the following decay is that of the previously well-studied

256

Lr. (The small amount

258

Lr is due to accidental coincidences. Finally, the chemical identity of the Lr

is conﬁrmed by the spectrum of x-rays following the atomic de-excitation. (The Lr

is generally left in an excited state after the decay of

260

Db.)

Exercises for Chapter 2 103

116

292

116

296

114

288

112

284

110

280

10.56 MeV

9.09 MeV

53.9 s

2.42 s

9.81 MeV

46.9 ms

221 MeV

14.3 s

116

292

116

296

114

288

112

284

110

280

10.56 MeV

9.09 MeV

53.9 s

2.42 s

9.81 MeV

46.9 ms

221 MeV

14.3 s

116

292

116

296

114

288

112

284

110

280

10.56 MeV

9.09 MeV

53.9 s

2.42 s

9.81 MeV

46.9 ms

221 MeV

14.3 s

116

July 19, 2000

May 2, 2001 May 8, 2001

detector

time−of−flight

beam

magnetic

quadrupole

248

target

electrostatic

deflectors

magnetic

quadrupole

magnetic

deflectors

array

detector

silicon

248

Cm +

296

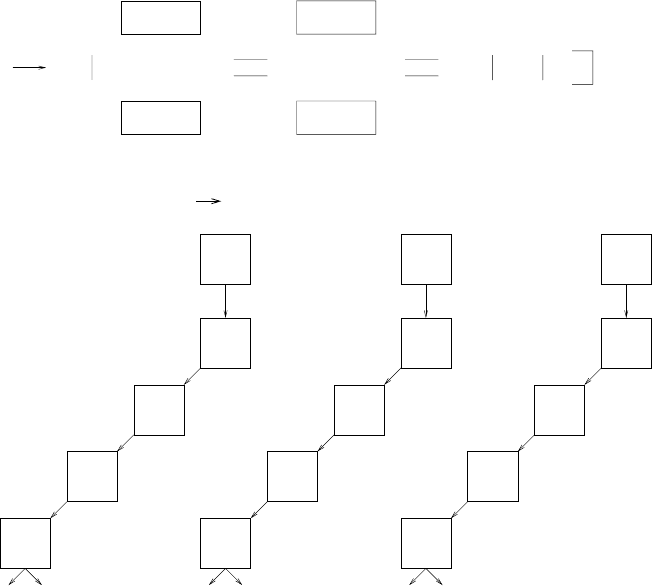
Fig. 2.20. The production of element 116 in

Ca-

248

Cm collisions. The top panel

shows the apparatus used by [29]. Inelastic collisions generally produce light ﬁssion

nuclei. Super-heavy nuclei are separated from these light nuclei by a system of mag-

netic and electrostatic deﬂectors and focusing elements. Nuclei that pass through

this system stop in a silicon detector array (Chap. 5) that measures the time, posi-

tion and deposited energy of the nucleus. Subsequent decays are then recorded and

the decay energies measured by the energy deposited in the silicon. The bottom

panel shows 3 observed event sequences that were ascribed in [29] to production and

decay of

296

116. The three sequences all have 3 α decays whose energies and decay

times are consistent with the hypothesis that the three sequences are identical.

104 2. Nuclear models and stability

2.2 TheradiusofanucleusisR  r

1/3

with r

=1.2fm.UsingHeisen-

berg’s relations, estimate the mean kinetic momentum and energy of a nu-

cleon inside a nucleus.

2.3 Consider the nucleon-nucleon interaction, and take the model V (r)=

(1/2)µω

− V

for the potential. Estimate the values of the parameters

ω and V

that reproduce the size and binding energy of the deuteron. We

recall that the wave function of the ground state of the harmonic oscillator is

ψ(r, θ, φ) ∝ exp(−mωr

/2¯h). Is a  = 1 state bound predicted by this model?

2.4 Consider a three-dimensional harmonic oscillator, V (r)=(1/2)mω

the energy eigenvalues are

=(n +3/2)¯hω n = n

+ n

, (2.69)

where n

x,y,z

are the quantum numbers for the three orthogonal directions

and can take on positive semi-deﬁnite integers. We denote the corresponding

eigenstates as |n

.Theysatisfy

x|n

 =

√

− 1

− 1,n

 +

√

+1,n

 ,

and

ip|n

 =

√

− 1

− 1,n

−

√

+1,n

 ,

where α =



2mω/¯h. Corresponding relations hold for y and z. These states

are not generally eigenstates of angular momentum but such states can be

constructed from the |n

. For example, verify explicitly that the E =

(1/2)¯hω and E =(3/2)¯hω states can be combined to form l = 0 and l =1

states:

|E =(1/2)¯hω, l =0,l

=0 = |0, 0, 0 ,

|E =(3/2)¯hω, l =1,l

=0 = |1, 0, 0 ,

|E =(3/2)¯hω, l =1,l

= ±1 =(1/

√

2) (|0, 1, 0±i|0, 0, 1) .

2.5 Verify equations (2.40).

2.6 Use Fig. 2.10 to predict the spin and parity of

Ca.

2.7 The nuclear shell model makes predictions for the magnetic moment of

a nucleus as a function of the orbital quantum numbers. Consider a nucleus

Exercises for Chapter 2 105

consisting of a single unpaired nucleon in addition to a certain number of

paired nucleons. The nuclear angular momentum is the sum of the spin and

orbital angular momentum of the unpaired nucleon:

J = S + L . (2.70)

The total angular momentum (the nuclear spin) is j = l ±1/2 for the nucleon

spin aligned or anti-aligned with the nucleon orbital angular momentum. The

two types of angular momentum do not contribute in the same way to the

magnetic moment:

µ = g

+ g

(2.71)

where m ∼ m

∼ m

is the nucleon mass, g

=1(g

= 0) for an unpaired

proton (neutron) and g

=2.792×2(g

= −1.913×2) for a proton (neutron).

The ratio between the magnetic moment and the spin of a nucleus is the

gyromagnetic ratio, g. It can be deﬁned as

g ≡

µ · J

J ·J

(2.72)

Use (2.40) to show that

g =(j −1/2)g

+(1/2)g

for l = j − 1/2 (2.73)

g =

j +1

[(j +3/2)g

− (1/2)g

]forl = j +1/2 . (2.74)

Plot these two values as a function of j for nuclei with one unpaired neutron

and for nuclei with one unpaired proton. Nuclei with one unpaired nucleon

generally have magnetic moments that fall between these two values, known

as the Schmidt limits.

Consider the two (9/2)

nuclides,

Kr and

Nb. Which would you ex-

pect to have the larger magnetic moment?

2.8 Verify (2.59) by using

lim

min

→0



min



−1

− 1du ∼





−1

− 1du −



min

√

−1

du.

2.9 To justify (2.55) write the wavefunction as

ψ(r)=C exp(−γ(r)) + D exp(+γ(r)) . (2.75)

In the WKB approximation, we suppose that ψ(r) varies suﬃciently slowly

that we can neglect (d

/dr

)γ(r) ∼ 0 . In this approximation, show that

∼ (

dγ

)

ψ (2.76)

106 2. Nuclear models and stability

and that the Schr¨odinger becomes

(

dγ

)

ψ +

¯h

(E −

2Ze

4π

)ψ =0, (2.77)

i.e.

(

dγ



¯h

(E −

2Ze

4π

) , (2.78)

which is the desired result.

3. Nuclear reactions

In the last chapter we studied how nucleons could combine with each other to

form bound states. In this chapter we consider how free particles and nuclei

can interact with each other to scatter or initiate nuclear reactions. The con-

cepts we will learn have great practical interest because they will allow us,

in later chapters, to understand the generation of thermal energy in nuclear

reactors and stars. However, in this chapter we will primarily be concerned

with learning how to obtain information about nuclear interactions and nu-

clear structure from scattering experiments. In such experiments, a beam of

free particles (electrons, nucleons, nuclei) traverses a target containing nuclei.

A certain fraction of the beam particles will interact with the target nuclei,

either scattering into a new direction or reacting in a way that particles are

created or destroyed.

Classically, the character of a force ﬁeld can be found by following the

trajectory of test particles. The oldest example is the use of planets and

comets to determine the gravitational ﬁeld of the Sun. The nuclear force can

not be studied directly with this technique because its short range makes it

impossible to follow trajectories through the interesting region where, in any

case, quantum mechanics limits the usefulness of the concept of trajectory.

It is generally only possible to measure the probability of a certain type

of reaction to occur. In such circumstances, it is natural to introduce the

statistical concept of “cross-section” for a given reaction.

Cross-sections will be discussed in general terms in the Sect. 3.1. The

sections that follow will present various ways of calculating cross-sections

from knowledge of the interaction Hamiltonian.

Section 3.2 will tackle the simple problem of a particle moving into a ﬁxed

potential well. The cross-section will be calculated ﬁrst supposing that the

particle follows a classical trajectory and then by using quantum perturba-

tion theory on plane waves. The use of perturbation theory will allow us to

treat both elastic and simple “quasi-elastic” collisions due to electromagnetic

or weak interactions. The section will end with a discussion of elastic scat-

tering of wave packets that will allow us to better understand the angular

distribution of scattered particles

The most important potential treated in Sect. 3.2 will be the Yukawa

potential

108 3. Nuclear reactions

V (r)=

g¯hc

exp(−r/r

) . (3.1)

As mentioned in Sect. 1.4, this potential describes the long-range component

of the nucleon–nucleon potential. Unfortunately, the dimensionless coupling

g is too large for the perturbative methods of Sect. 3.2 to be applicable. The

interest of the Yukawa potential in this section will be rather the two limits

→∞and r

→ 0. In the ﬁrst limit the Yukawa potential becomes the

Coulomb potential

V (r)=

g¯hc

g = Z

α, (3.2)

where Z

and Z

are the charges of the interacting particles and α =

/4π

¯hc ∼ 1/137 is the ﬁne structure constant. In the other limit r

→ 0,

the potential is

V (r)=4πGδ

(r) G = g¯hcr

. (3.3)

This potential is useful in discussing weak-interaction processes where G is of

order the Fermi constant G

. The techniques of Sect. 3.2 will therefore allow

us to treat scattering and reactions due to the weak and electromagnetic

interactions.

Section 3.4 will show how to take into account the fact that the scatter-

ing potential is not ﬁxed, but due to a particle that will itself recoil from

the collision. This will allow us to treat processes where the target is a com-

plicated collection of particles that can be perturbed by the beam particle.

With these techniques, we will learn how it is possible to determine the charge

distribution in nuclei.

Section 3.5 will show how short-lived “resonances” can be produced during

collisions.

Section 3.6 will introduce the more diﬃcult problem of nucleon–nucleon

and nucleon–nucleus scattering where the interaction potential can no longer

be considered as weak. This problem will complete our treatment of the

deuteron in Sect. 1.4.

Finally, in Sect. 3.7 we will learn how coherent forward scattering in a

medium leads to a neutron refractive index. An application of this subject

will be the production of ultra low-energy neutron beams.

3.1 Cross-sections

3.1.1 Generalities

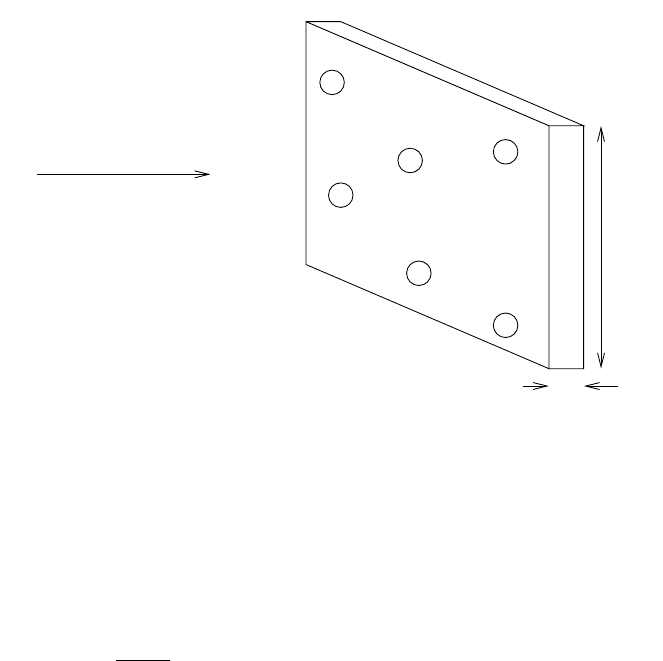
To introduce cross-sections, it is conceptually simplest to consider a thin slice

of matter of area L

containing N spheres of radius R, as shown in Fig. 3.1.

A point-like particle impinging upon the slice at a random position will have

3.1 Cross-sections 109

Fig. 3.1. A small particle incident on a slice of matter containing N = 6 target

spheres of radius R. If the point of impact on the slice is random, the probability

dP of it hitting a target particle is dP = NπR

= σndz where the number

density of scatterers is n = N/(L

dz) and the cross section per sphere is σ = πR

a probability dP ofhittingoneofthespheresthatisequaltothefractionof

the surface area covered by a sphere

dP =

NπR

= σndzσ= πR

. (3.4)

In the second form, we have multiplied and divided by the slice thickness dz

and introduced the number density of spheres n = N/(L

dz). The “cross-

section” for touching a sphere, σ = πR

, has dimensions of “area/sphere.”

While the cross-section was introduced here as a classical area, it can be

used to deﬁne a probability dP

for any type of reaction, r, as long as the

probability is proportional to the number density of target particles and to

the target thickness:

= σ

n dz. (3.5)

The constant of proportionality σ

clearly has the dimension of area/particle

and is called the cross-section for the reaction r.

If the material contains diﬀerent types of objects i of number density and

cross-section n

and σ

, then the probability to interact is just the sum of the

probabilities on each type:

dP =



(3.6)